Лабораторная работа №4. Лабораторная работа 4. Прогнозирование и планирование временных рядов
 Скачать 171.65 Kb. Скачать 171.65 Kb.
|
|
Лабораторная работа №4. Прогнозирование и планирование временных рядов. Этап 1. Оценка наличия тренда и построение трендовой модели. По данным о средних доходах на конечное потребление за десять лет, которые представлены в табл. 1, оцените наличие тренда и в случае положительного ответа постройте трендовую модель. Таблица 1 Расходы на конечное потребление, тыс. у.е.
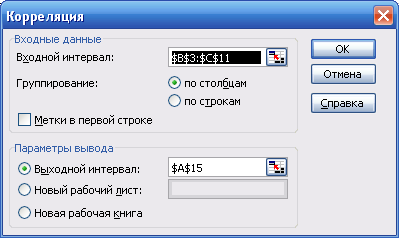
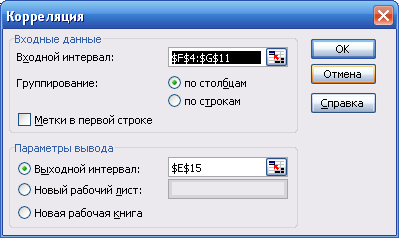
Ход решения. Для формального определения структуры временного ряда проводится автокорреляционный анализ уровней временного ряда. С этой целью рассчитываются коэффициенты автокорреляции уровней временного ряда. Расчет автокорреляционной функции можно осуществлять на компьютере средствами Excel: Анализ данных / Корреляция. На рис. 1 представлены диалоговые окна расчета коэффициентов автокорреляции первого и второго порядков временного ряда yt.
Рис. 1. Диалоговые окна расчета коэффициента автокорреляции первого и второго порядков ряда yt В табл. 2 представлены результаты расчетов. Таблица 2 Результаты расчетов коэффициентов автокорреляции.
Поскольку коэффициенты автокорреляции первых порядков (r1, r2) являются высокими, можно предположить наличие линейного тренда Т = а + bt. Определите уравнение линейного тренда. Для этого: 1. Постройте диаграмму по значениям временного ряда yt. (тип Точечная). 2. Нажмите правой кнопкой мыши на одной из точек данных на диаграмме. В открывшемся меню необходимо выбрать команду Добавить линию тренда. На экране появится диалоговое окно Линия тренда. 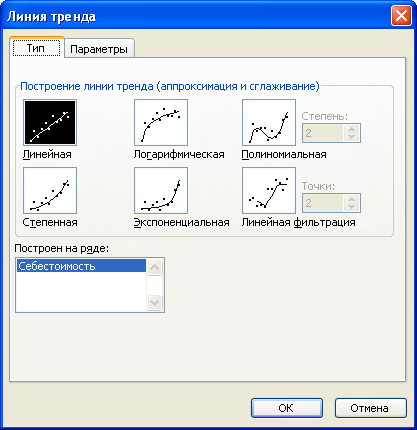 Рис. 2. Диалоговое окно построения линии тренда 3. Выберете тип регрессии. Например, линейная. 4. Переключитесь на вкладку Параметры. В разделе Название аппроксимирующей (сглаженной) кривой установите переключатель автоматическое, установите отображение на диаграмме уравнения и величины достоверности аппроксимации. Аналогично постройте линию тренда, в качестве функции выбрать степенную. Замечание: Уравнение линейного тренда можно получить, используя инструмент Регрессия - Пакета анализа. Этап 2. Сглаживание данных и построение прогноза Провести сглаживание данных рассматриваемой задачи и выполнить прогноз на период t=11. Скопируйте условие предыдущего примера на Лист 2. (Диапазон A1:B11) С помощью пакета анализа рассчитайте значения скользящего среднего (инструмент «скользящее среднее»). Заполните диалог следующим образом: входной интервал - $В$2:$В$11, интервал - 3, выходной интервал -$С$3, установите флажок Вывод графика. Удалите значения равные #Н/Д. Результаты оформите в таблицу с тремя столбцами: t, yt, Прогноз (скользящ.) Скорректируйте построенный график таким образом, чтобы по оси X были значения t (от 1 до 11), по оси У – значения скользящего среднего. График фактических значений yt должен быть построен для дней, начиная с 1-го по 10-ый, график прогнозируемых значений должен быть построен для дней начиная с 4-го по 11-ый. С помощью пакета анализа рассчитайте значения экспоненциального сглаживания (инструмент «экспоненциальное сглаживание»). Заполните диалог следующим образом: входной интервал - $В$2:$В$11, фактор затухания - 0,25, выходной интервал - $D$2, установите флажок Вывод графика. Удалите значения равные #Н/Д. Продлите значения рассчитанного столбца для получения прогноза на 11-й день. Назовите столбец Прогноз (экспоненц.). Скорректируйте построенный график таким образом, чтобы по оси X были значения дней (от 1 до 11), по оси У – спрогнозированные значения. График фактических значений yt должен быть построен для дней, начиная с 1-го по 10-ый, график прогнозируемых значений должен быть построен для дней начиная с 2-го по 11-ый. Сформулируйте экономический смысл полученных моделей. Объясните механизм прогнозирования в каждой их них. Этап 3. Исследование структуры временного ряда. По данным табл. 3 исследуйте структуру временного ряда по квартальным данным потребления электроэнергии за 2001 – 2004 гг. Оцените уровень и структуру потребления электроэнергии в 2005 г. Таблица 3 Исходные данные
Ход решения. В данной задаче в качестве зависимой переменной у выступает потребление электроэнергии, в качестве независимой переменной — время t ( Первоначально изобразите ряд графически. Постройте диаграмму по исходным данным задачи. Тип диаграммы – график с маркерами. Периоды от 1 до 16 использовать в качестве подписи по оси Х. Попробуйте пообобрать линию тренда на построенном графике. 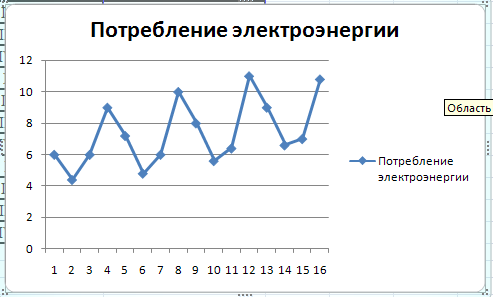 Рис. 3. График потребления электроэнергии за I кв. 2001 г. - IV кв. 2004 г. Из рис. 3 видно, что в IV кв. потребление электроэнергии каждый год возрастает, поэтому есть подозрение на наличие сезонной компоненты в ряде. Визуально также Видно, что амплитуда сезонных колебаний постоянна, что позволяет предположить аддитивную структуру временного ряда у = Т + S + Е. Решение задачи (с расчетом сезонных компонент). Для расчета сезонных компонент воспользуемся методом скользящей средней. Просуммируем уровни ряда последовательно за каждые четыре квартала со сдвигом на один момент времени и определим условные годовые объемы потребления электроэнергии (гр. 3 табл. 4). Полученные суммы разделим на длину периода (в нашем случае на 4) и найдем скользящие средние, которые уже не зависят от сезонности (гр. 4 табл. 4). Чтобы привести эти значения в соответствие с фактическими моментами времени, найдем средние значения из каждых двух соседних скользящих средних (гр. 5 табл. 4). Оценку сезонной компоненты найдем, вычитая из фактического значения уровня ряда у, центрированную скользящую среднюю (гр. 6 табл. 4). Таблица 4 Исходные данные
На следующем этапе подготовим вторую вспомогательную табл. 5. Занесем в нее оценки сезонных компонент, распределив их по кварталам. За каждый квартал найдем среднюю оценку сезонной компоненты. Например, для I кв. Сезонные воздействия за период должны взаимопогашаться. В аддитивной модели это выражается в том, что сумма всех сезонных компонент за период должна быть равна нулю. Рассчитаем корректирующий коэффициент по формуле Для нашего примера k = (0,6 - 1,958 - 1,275 + 2,708) / 4 = 0,01875. Скорректированные значения сезонной компоненты рассчитываем как разность между средним значением сезонной компоненты и корректирующим коэффициентом Таблица 5
Элиминируем сезонную компоненту из исходного ряда, т.е. рассчитаем у - S. С этой целью заполним рабочую табл. 6.: Таблица 6
Далее в преобразованном ряду у — S можно выделить линейный тренд. Зная значения сезонных компонент 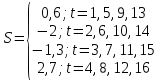 и тренд y=a+bt, можно прогнозировать потребление электроэнергии в каждом квартале с использованием модели у = a+bt + St. Задание для самостоятельной работы. 1.По данным о выпуске продукции за десять лет, которые представлены в таблице, оцените наличие тренда и в случае положительного ответа постройте трендовую модель (Вариант выбирается по последней цифре номера зачетной книжки).
2.По данным задания 1 проведите сглаживание данных и выполните прогноз на период t=11. 3.В таблице имеются данные об объеме экспорта по кварталам за 2000 — 2005 гг. Постройте аддитивную модель временного ряда и спрогнозируйте экспорт по кварталам на 2006 г. Таблица
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||