лабораторная 5. лаба 5.1 Олег С.. Лабораторная работа 5. 1 Изучение свободных колебаний в электрическом контуре садыкбаев Олег Станиславович Группа мо15
 Скачать 1.09 Mb. Скачать 1.09 Mb.
|
|
Кафедра Физики Лабораторная работа №5.1 ИЗУЧЕНИЕ СВОБОДНЫХ КОЛЕБАНИЙ В ЭЛЕКТРИЧЕСКОМ КОНТУРЕ Выполнил: Садыкбаев Олег Станиславович Группа:МО-15 Проверил: Черевко Александр Григорьевич Измерения сняты Дата, роспись преподавателя Отчёт принят Дата, роспись преподавателя Работа зачтена Оценка, дата, роспись преподавателя КРАТКАЯ ТЕОРИЯ Исследуемый контур состоит из конденсатора электроемкостью С, катушки с индуктивностью L и резистора, имеющего сопротивление R. Схема соединения элементов электрической цепи приведена на рисунке 1. 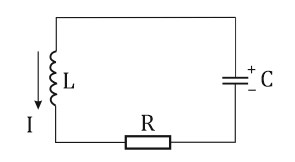 Рис. 1 Схема реального колебательного контура Простой контур, который здесь рассматривается, является электрической цепью со сосредоточенными параметрами. Это означает, что электроемкость С сосредоточена в одном месте (конденсаторе), а индуктивность L и сопротивление R - в других местах контура (в катушке и в резисторе). Электрическими колебаниями в таком случае выступают повторяющиеся изменения электрических величин, характеризующих процессы в элементах контура. В конденсаторе, например, изменяются со временем следующие величины: заряд q и напряжение между обкладками 𝑈с а также характеристики электрического поля конденсатора. Электрические колебания (процессы) происходят во всех элементах цепи согласованно. А именно так, что мгновенные значения силы тока I одни и те же в любом месте контура. Подобное имеет место в цепи постоянного (стационарного) тока. Поэтому электрические процессы в колебательном контуре называются квазистационарными («квази»- приставка, означающая «якобы, как будто»). Квазистационарные процессы также подчиняются закону Ома, что и постоянный ток. Для математического описания электрических процессов в контуре применим 2 правило Кирхгофа: «Сумма падений напряжения в контуре равна сумме действующих в нем ЭДС». В колебательном контуре имеются два 𝑞 падения напряжения: на конденсаторе 𝑈с, равное 𝐶, и на сопротивлении, равное IR. При изменении силы тока в контуре в катушке индуктивности возникает ЭДС самоиндукции. 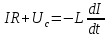 (1) (1) Сила тока по определению связана с зарядом конденсатора соотношением: 𝑑𝑞 𝐼 =  или 𝐼 = 𝑞′ - так обозначается производная по времени. или 𝐼 = 𝑞′ - так обозначается производная по времени. 𝑑𝑡 Подставив выражения для тока i и напряжения 𝑈с в формулу (1), получим дифференциальное уравнение в виде: 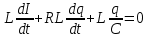 Разделим уравнение на коэффициент при старшей производной (индуктивность катушки) и введем обозначения:  После введения обозначений дифференциальное уравнение затухающих колебаний в контуре принимает вид:  (2) Функция  (3) является решением дифференциального уравнения (2) и называется уравнением затухающих колебаний заряда конденсатора. Циклическая частота затухающих колебаний  (4) Амплитуда заряда на конденсаторе убывает со временем по экспоненциальному закону:  (5) (5) Быстрота убывания определяется величиной β, которую называют коэффициентом затухания.  Так как 𝜔 есть действительное число и 𝜔2 не может быть отрицательным, то затухающие колебания имеют место только при условии (см.4): 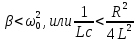 (7) Наконец, постоянные величины 𝑞0 и 𝜑0 определяются начальными условиями. Если, например, вначале при разомкнутом контуре конденсатор заряжен (𝑞0- величины заряда), а потом соединен с катушкой и резистором, то начальная фаза колебаний равна нулю, то есть 𝜑0=0. На рисунке 2 показаны графики затухающих колебаний в одном электрическом контуре при двух значениях коэффициента затухания. Причем, 𝛽2 > 𝛽1, а величины 𝑞0и 𝜑0 одинаковы. Пунктиром изображена зависимость амплитуды заряда 𝑞𝑚 от времени. Эта зависимость называется экспоненциальной.  Рис. 2 Графики затухающих колебаний заряда с разными коэффициентами затуханий Теперь обратим внимание на такие особенности колебательного процесса с затуханием, которые на рисунке заметить нельзя. Для этого найдем уравнение колебаний тока в контуре, приняв уравнение колебаний заряда в виде 𝑞0𝑒−𝛽𝑡 cos 𝜔𝑡. Так как 𝐼 = 𝑞′, то после дифференцирования получим:  Записав слагаемое 𝜔 sin 𝜔𝑡 как 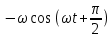 и складывая оба и складывая оба слагаемых выражения в скобках с помощью векторной диаграммы, получим уравнение колебаний тока в виде: 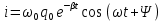 (6) (6) Полученный результат приводит к следующим заключениям: Амплитуда тока в начальный момент времени 𝐼0 = 𝜔0𝑞0 не зависит от характеристик затухания. В контурах с малым сопротивлением R и достаточно большой частотой 𝜔 реализуется неравенство: 𝛽 ≪ 𝜔. Это случай слабого затухания, величина сдвига фаз Ψ стремится к Полученная ранее формула (4) позволяет рассчитать относительную разницу величин 𝜔0и 𝜔 с помощью соотношения:  В результате при СЛАБОМ ЗАТУХАНИИ уравнения колебаний заряда и тока можно приближенно записать так:   Отметим, что период колебаний  определяется в этом случае известной формулой Томсона: определяется в этом случае известной формулой Томсона: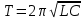 Точное же значение периода затухающих колебаний (в соответствии с формулой (4)) равно 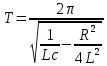 Вернемся еще раз к экспоненциальной зависимости 𝑞𝑚 = 𝑞0𝑒−𝛽𝑡, изображенной на рис. 2, чтобы рассказать о других важных характеристиках затухающих колебаний и дать им физическое объяснение. Непрерывное рассеяние энергии на сопротивлении приводит к тому, что наибольший заряд конденсатора уменьшается с каждым периодом колебаний, именно: qm(0) > qm(T) > qm(2T) > ...qm(NT) > ..., N - число колебаний. Эти амплитуды колебаний образуют убывающую геометрическую прогрессию. А это означает, что отношение величины каждого максимума 𝑞𝑚(𝑡)к последующему 𝑞𝑚( t+T) одинаково. Безразмерная величина, равная натуральному логарифму отношения амплитудных значений, отстоящих по времени на период колебания, называется логарифмическим декрементом затухания:  (10) (10) С логарифмическим декрементом затухания связана (обратно пропорциональной зависимостью) еще одна характеристика затухающих колебаний - добротность Q. (Не путать с зарядом q!). В случае слабого затухания добротность определяется следующим образом: |
| C, нФ | L, мГн | N | n | γ, мкс/дел | t, мкс |  , ,мкс |  , ,мкс | 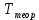 , ,мкс |
| 10,04 | 19,1 | 11 | 10 | 100 | 1000 | 90,91 | 13,85 | 87,01 |
| 15,1 | 19,1 | 9 | 10 | 100 | 1000 | 111,11 | 16,98 | 106,71 |
| 20 | 19,1 | 7 | 9 | 100 | 900 | 128,57 | 19,55 | 122,80 |
| 25,1 | 19,1 | 7 | 10 | 100 | 1000 | 142,86 | 21,90 | 137,57 |
| 30,1 | 19,1 | 7 | 11 | 100 | 1100 | 158,57 | 23,98 | 150,65 |
| 36,2 | 19,1 | 3 | 5 | 100 | 500 | 166,67 | 26,3 | 165,22 |

Задание №3
 ,
,  мГн,
мГн, нФ
нФ 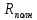 , ,Ом | N |  , ,дел |  , ,дел | 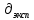 | 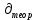 |  | 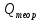 |
| 21,22 | 22 | 3 | 1 | 0,0499 | 0,0682 | 62,96 | 46,05 |
| 43,82 | 14 | 2 | 0,5 | 0,0990 | 0,1408 | 31,73 | 22,30 |
| 75,82 | 7 | 3,5 | 1 | 0,1790 | 0,2437 | 17,55 | 12,89 |
| 130,12 | 4 | 3.5 | 1 | 0,3132 | 0,4183 | 10,03 | 7,51 |
| 232,22 | 2 | 3.2 | 0.8 | 0,6932 | 0,7465 | 4,53 | 4,21 |
Контрольные вопросы
1)Возьмём за скорость сигнала – скорость света.
t = s/v; s = 0.1 (м), v = 3 * 10^8 (м/с);
t = 0.1/3*10^8 = 3.33*10^-10 (c) = 0.33 (нс);
MaxЧастота = 1/t*2 = 1500000015 (Гц) = 1,5 (ГГц);
2)Закон Ома, Кирхгофа. Законы о магнитной индукции катушки. Законы о напряжённости поля, о ёмкости, да и вообще многие законы электромагнитных полей и электрических контуров.
3)Там присутствует ещё одно слагаемое
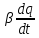 ,
, 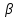 – коэффициент затухания. Он равен
– коэффициент затухания. Он равен  , то есть отличие заключается в наличие активного сопротивления.
, то есть отличие заключается в наличие активного сопротивления.4)Как я понимаю от коэффициента затухания и частоты затухания, то есть от
 и
и  , но частота затухания равна
, но частота затухания равна  , только в случае слабого затухания, потому что при нём, добротность высока и частота затухания практически равна частоте без сопротивления.
, только в случае слабого затухания, потому что при нём, добротность высока и частота затухания практически равна частоте без сопротивления.
5) Это время, за которое амплитуда колебаний уменьшается в e раз.
Чем больше сопротивление контура, тем быстрее будет убывать энергия, а следовательно амплитуда колебаний и время релаксации.
6)Как я понимаю уменьшение амплитуды колебаний. Логарифмический декремент затухания есть величина, обратная времени, за которое амплитуда колебаний уменьшается в e раз.
7)В случае слабого затухания вот такая
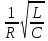
8)
а)При слабом затухании
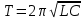 , при сильном затухании частота затуханий уже сильно отлична от частоты колебаний в идеальных условиях по этому там добавятся ещё переменные.
, при сильном затухании частота затуханий уже сильно отлична от частоты колебаний в идеальных условиях по этому там добавятся ещё переменные.б)В случае слабого затухания
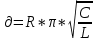
Больше
 ,больше и R это очевидно ведь увеличивается емкость и индуктивность что увеличивает кол-во энергии свободных колебаний.
,больше и R это очевидно ведь увеличивается емкость и индуктивность что увеличивает кол-во энергии свободных колебаний.Чем больше R тем больше логарифмический декремент затухания, тоже логично, ведь чем больше активное сопротивление контура, тем быстрее убывает энергия контура, а значит быстрее затухают колебания, а значит повышается логарифмический декремент затухания.
Задача

Вывод:
Значения ёмкости и индуктивности сильно влияют на период колебаний в случае малого сопротивления по закону
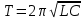
В случае слабого затухания зависимость логарифмического декремента затухания от R это прямая зависимость.

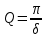
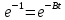



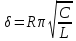

 (15)
(15) (16)
(16) 
 величину 𝑅кр называют критическим сопротивлением контура.
величину 𝑅кр называют критическим сопротивлением контура. 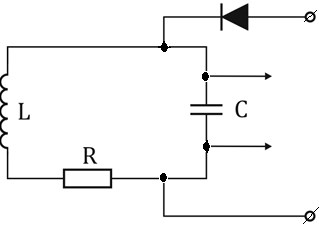

 ). По горизонтальной оси отложено время t, по вертикальной оси отложено напряжение на конденсаторе Uc. Время по горизонтальной оси можно рассчитать. Для этого поверх экрана нанесена прямоугольная сетка, калиброванная в единицах времени (мс или мкс). Назовем временную длительность одного квадрата сетки по горизонтали ценой деления развертки и обозначим ее 𝛾. Для более точного измерения каждое деление «разделено» на доли по 0,2 (это указано на сетке). Тогда время t, в течение которого происходят N колебаний, будет равно t=n, где n-
). По горизонтальной оси отложено время t, по вертикальной оси отложено напряжение на конденсаторе Uc. Время по горизонтальной оси можно рассчитать. Для этого поверх экрана нанесена прямоугольная сетка, калиброванная в единицах времени (мс или мкс). Назовем временную длительность одного квадрата сетки по горизонтали ценой деления развертки и обозначим ее 𝛾. Для более точного измерения каждое деление «разделено» на доли по 0,2 (это указано на сетке). Тогда время t, в течение которого происходят N колебаний, будет равно t=n, где n- 
