22_Ермилов_Ярослав_МП-14_Лаб.№9 ( ). 22_Ермилов_Ярослав_МП-14_Лаб.№9 (+). Лабораторная работа 5 9 Ярослав Ермилов ( мп14 ) Лабораторная работа 9 Работу Ермилов Ярослав (мп14)
 Скачать 72.73 Kb. Скачать 72.73 Kb.
|
Лабораторная работа №9Работу выполнил: Ермилов Ярослав (МП-14) Упражнение 1.Вычислить значения полинома 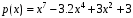 в точках в точках 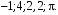 Значения аргументов задать в виде вектора. Сохранить значения полинома. Значения аргументов задать в виде вектора. Сохранить значения полинома. >> p=[1 0 0 -3.2 0 3 0 3]; >> p1=polyval(p,-1) p1 = 1.8000 >> p2=polyval(p,4) p2 = 1.5616e+004 >> p3=polyval(p,2.2) p3 = 191.9939 >> p4=polyval(p,pi) p4 = 2.7412e+003 Упражнение 2.Вычислить корни полинома 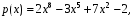 сохранить их, сделать проверку. сохранить их, сделать проверку.>> p=[2 0 0 -3 0 0 7 0 -2]; >> roots(p) ans = -0.958588470427180 + 0.795177563517093i -0.958588470427180 - 0.795177563517093i -0.151418027911906 + 1.253568731141242i -0.151418027911906 - 1.253568731141242i 1.092703966134577 + 0.467826831909836i 1.092703966134577 - 0.467826831909836i -0.517938773966140 0.552543838375159 >> poly(ans) ans = Columns 1 through 3 1.000000000000000 -0.000000000000002 -0.000000000000001 Columns 4 through 6 -1.499999999999995 0.000000000000002 0.000000000000012 Columns 7 through 9 3.499999999999990 -0.000000000000003 -0.999999999999998 Упражнение 3.Вычислить произведение полиномов 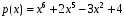 и и 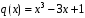 , ,а также частное и остаток от деления 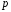 на на 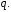 >> p=[1 2 0 0 -3 0 4]; >> q=[1 0 -3 1]; >> conv(p,q) ans = 1 2 -3 -5 -1 0 13 -3 -12 4 >> deconv(p,q) ans = 1 2 3 5 Упражнение 4.Написать файл-функцию с двумя аргументами, осуществляющую сложение полиномов разной степени. Алгоритм: 1) Найти большую из длин входных аргументов (обозначим её  2) Создать вспомогательные векторы длины 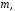 представляющие те же самые полиномы, что и аргументы. Для заполнения части элементов нулями можно использовать функцию zeros. представляющие те же самые полиномы, что и аргументы. Для заполнения части элементов нулями можно использовать функцию zeros.3) Вычислить сумму. Протестировать файл-функцию, используя полиномы 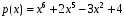 и и 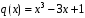 , ,function f=summa(p,q) if length(p)==length(q) f=q+p; else if length(p)>length(q) M=p; m=q; else M=q; m=p; end L=length(M); l=length(m); s=0; for i=1:1:L if i<=(L-l) N(i)=0; else s=s+1; N(i)=m(s); end end f=N+M; end end >> p p = 1 2 0 0 -3 0 4 >> q q = 1 0 -3 1 >> summa(p,q) ans = 1 2 0 1 -3 -3 5 Упражнение 5.Для многочленов  и и 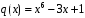 найти их производные, производную произведения и частного. найти их производные, производную произведения и частного.>> p=[1 -1 0 -3 0 -2]; >> q=[1 0 0 0 0 -3 1]; >> polyder(p) ans = 5 -4 0 -6 0 >> polyder(q) ans = 6 0 0 0 0 -3 >> polyder(p,q) ans = 11 -10 0 -24 0 -30 20 -4 27 -6 6 >> [n d]=polyder(p,q) n = -1 2 0 12 0 0 14 -4 9 -6 -6 d = Columns 1 through 12 1 0 0 0 0 -6 2 0 0 0 9 -6 Column 13 1 Упражнение 6.Создать файл-функцию, вычисляющую производную порядка n полинома 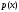 , заданного вектором коэффициентов. Производную задать вектором коэффициентов. С помощью созданной файл-функции найти 5-ую производную полинома , заданного вектором коэффициентов. Производную задать вектором коэффициентов. С помощью созданной файл-функции найти 5-ую производную полинома 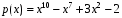 и вычислить её значение в точке 0,2. и вычислить её значение в точке 0,2.function r=polydiff(polynom,n) for i=1:n polynom=polyder(polynom); end r=polynom; end >> p=[1 0 0 -1 0 0 0 0 3 0 -2]; >> polydiff(p,5) ans = 30240 0 0 -2520 0 0 >> polyval(ans,0.2) ans = -91.123199999999997 Упражнение 7.Создать М-файл, вычисляющий значения коэффициентов 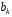 (в виде вектора) в многочлене Тейлора для полинома произвольной степени в произвольной точке. С помощью созданной функции вычислить коэффициенты (в виде вектора) в многочлене Тейлора для полинома произвольной степени в произвольной точке. С помощью созданной функции вычислить коэффициенты 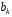 для разложений полинома для разложений полинома 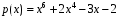 в многочлен Тейлора по степеням в многочлен Тейлора по степеням 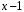 и и 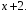 function f=taylor2(p,x0) n=length(p); for i=n:-1:1 if i==1 b(i)=polyval(p,x0); else %fac=1; %for j=1:i % fac=fac*j; %end b(i)=(polyval(polydiff(p,i-1),x0))/factorial(i-1); end end f=b; end >> p=[1 0 2 0 0 -3 -2] p = 1 0 2 0 0 -3 -2 >> taylor2(p,1) ans = -2.0000 5.5000 9.0000 7.0000 3.4000 1.0000 0.1429 >> taylor2(p,-2) ans = 100.0000 -129.5000 96.0000 -44.0000 12.4000 -2.0000 0.1429 Упражнение С1.Вычислить корни полинома 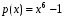 сохранить их, сделать проверку. сохранить их, сделать проверку.>> p=[1 0 0 0 0 0 -1]; >> roots(p) ans = -1.0000 -0.5000 + 0.8660i -0.5000 - 0.8660i 0.5000 + 0.8660i 0.5000 - 0.8660i 1.0000 >> poly(ans) ans = 1.0000 -0.0000 -0.0000 -0.0000 -0.0000 -0.0000 -1.0000 Упражнение С2.Вычислить произведение полиномов 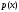 и и  , частное и остаток от деления , частное и остаток от деления 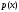 на на  , сумму полиномов, если , сумму полиномов, если 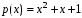 и и 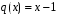 . .>> p=[1 1 1]; >> q=[1 -1]; >> conv(p,q) ans = 1 0 0 -1 >> [n d]=deconv(p,q) n = 1 2 d = 0 0 3 >> summa(p,q) ans = 1 2 0 Упражнение С3.Для многочлена 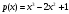 записать многочлен Тейлора по степеням записать многочлен Тейлора по степеням 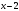 . . >> p=[1 -2 0 1] p = 1 -2 0 1 >> taylor2(p,2) ans = 1.0000 2.0000 1.3333 0.2500 -- |
