Лабораторная работа 5 (1). Лабораторная работа 5 Двоичнодесятичная арифметика Теория и методические указания
 Скачать 106.61 Kb. Скачать 106.61 Kb.
|
|
Лабораторная работа №5 «Двоично-десятичная арифметика» Теория и методические указания В ЭВМ применяют двоично-десятичные коды (BCD – Binary Coded Decimal или D-коды). В них каждая десятичная цифра кодируется двоичным числом из четырех битов (тетрадой), то есть отдельная тетрада – это запись одной цифры двоичными символами. 234= 0010 0011 0100 Тетраду можно записать в следующем виде: 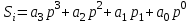 (1) (1)ai– коэффициенты, pi – двоичное основание системы счисления. Общие требования к двоично-десятичным кодам: Любая цифра D-кода должна изображаться однозначно. Должны легко обнаруживаться границы между цифрами. Большей цифре должно соответствовать большее значение тетрады. D-коды делятся на взвешанные и невзвешанные. Наиболее естественным представляется кодирование десятичных цифр позиционными двоичными кодами с естественными весами разрядов. Такой код принято называть кодом "8421" и он явяляется взвешанным. К невзвешанным кодам относятся коды "8421+3" и "8421+6". Основной недостаток кодирования десятичных цифр в коде "8421" состоит в несоответствии веса десятичного и шестнадцатеричного переносов. Действительно, перенос из тетрады шестнадцатеричной цифры имеет вес 16 а десятичный перенос - 10. Для устранения этого противоречия можно выбрать другие способы кодирования десятичных цифр. Например, код "8421+3" (иногда его называют код с избытком три) позволяет при сложении получать сумму "с избытком 6", при этом вес переноса соответствует десятичному, либо код "8421+6". В таблице 1 приведены упомянутые двоичные коды десятичных цифр. Таблица 1- Двоичные коды десятичных цифр
Арифметические операции над десятичными числами можно выполнять как на специальных десятичных сумматорах (в этом случае можно применять любую кодировку десятичных цифр), так и на обычных двоичных сумматорах. В последнем случае десятичные числа обрабатываются по правилам двоичной арифметики, и десятичный результат операции, естественно, нуждается в коррекции. В этом случае сложность коррекции и длительность ее реализации существенно зависят от выбранного кода. Правила сложения в D-кодах: Сложение производится потетрадно. В тетраде сложение производится по правилам двоичной арифметики. При рассмотрении D-кодов выделяют разрешенные и запрещенные комбинации. Комбинации цифр, указанные в таблице 1 – это разрешенные комбинации, остальные комбинации, образующиеся в результате потетрадного сложения свидетельствуют о необходимости введения коррекции результата и являются запрещенными. Правила сложения в коде "8421" Если сумма тетрад, представляющих соответствующие десятичные разряды слагаемых, больше 9, но не превышает 15, двоичный перенос в следующую тетраду не формируется. В этом случае требуется выработать искусственный перенос и удалить из тетрады 10, что соответствует добавлении шестерки (0110) и передаче обязательно возникающего при этом переноса в следующий старший разряд. Если из тетрады был двоичный перенос (в примере он отмечен знаком ←), то он "унес" из тетрады 16, в то время как десятичный перенос должен "уносить" только 10. Следовательно, в такие тетрады, из которых был перенос, следует добавить шестерку (0110). Таким образом, коррекция предварительной двоичной суммы при использовании кода "8421" заключается в добавлении кода 0110 ко всем тетрадам предварительной суммы, значение которых превышает 9 или из которых был двоичный перенос. Возникающие при коррекции переносы должны обязательно передаваться в следующую старшую тетраду. Выполним операции примера 1 с учетом сформулированных правил коррекции. 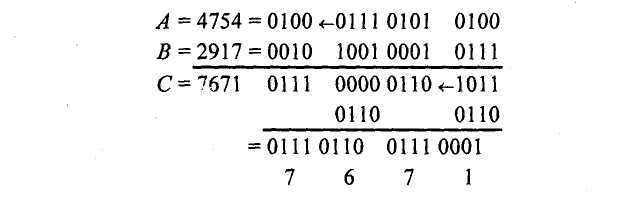 Правила сложения в коде "8421+3" Код "8421+3" (пример 2). При кодировании с избытком три каждая десятичная цифра представляется как 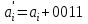 , где , где 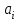 - код "8421" цифры. Тогда при сложении - код "8421" цифры. Тогда при сложении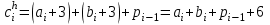 (1) (1)где 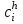 - предварительная сумма для всех комбинаций десятичных слагаемых, для которых - предварительная сумма для всех комбинаций десятичных слагаемых, для которых 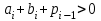 , значение , значение 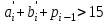 . Однако если переноса из тетрады не было, то результат сформируется "с избытком 6", поэтому потребуется коррекция тетрады предварительной суммы - удаление из тетрады лишней тройки. Вычитание (- 3) можно заменить сложением в дополнительном коде. . Однако если переноса из тетрады не было, то результат сформируется "с избытком 6", поэтому потребуется коррекция тетрады предварительной суммы - удаление из тетрады лишней тройки. Вычитание (- 3) можно заменить сложением в дополнительном коде. Итак, коррекции при сложении в коде "8421+3" подлежат все тетрады предварительной суммы, причем к тем тетрадам, из которых сформировался перенос, следует добавить константу 0011, а к тетрадам, из которых не было переноса, добавить константу 1101. Возникающие при коррекции межтетрадные переносы игнорируются! Пример 2.  Правила сложения в коде "8421+6" При кодировании с избытком шесть первая десятичная цифра представляется как 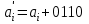 , , 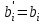 , где , где 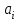 , bi - код "8421" цифры. , bi - код "8421" цифры. где 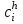 - предварительная сумма для всех комбинаций десятичных слагаемых, для которых - предварительная сумма для всех комбинаций десятичных слагаемых, для которых 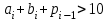 . Однако если перенос из тетрады был, то коррекция не выполняется. . Однако если перенос из тетрады был, то коррекция не выполняется. Итак, коррекции при сложении в коде "8421+6" подлежат тетрады предварительной суммы, из которых не было переноса: для этого необходимо добавить константу 1010 (-6). Возникающие при коррекции межтетрадные переносы игнорируются! Задание на выполнение Сложить числа А и В в коде (8-4-2-1), (8-4-2-1)+3, (8-4-2-1)+6. Разработать структуру АЛУ для заданного алгоритма. Составить микропрограмму работы АЛУ для заданного алгоритма. Варианты задания
Контрольные вопросы Правила сложения в D-кодах. Список учебно-методической и дополнительной литературы Таненбаум Э. Архитектура компьютера. 4-е издание. - СПб: Питер, 2003.-704 с.: ил. Хамахер К., Вранешич З., Заки С. Организация ЭВМ. 5-е издание. - СПб., Питер; Киев:Издательская группа BHV, 2003.-848 с.: ил. К. Цилькер. Организация ЭВМ и систем. Учебное пособие для вузов.–СПб.:Питер, 2004. – 635с. |
