лаба 5 программирование. Лабораторная работа 5 Линейные групповые коды Цель работы Закрепление знаний по методам кодирования информации. Задание
 Скачать 27.91 Kb. Скачать 27.91 Kb.
|
|
ЛАБОРАТОРНАЯ РАБОТА № 5 Линейные групповые коды Цель работы: Закрепление знаний по методам кодирования информации. Задание: 1. Построить линейный групповой код, способный исправлять одиночную ошибку. Вариант взять из лабораторной № 4. Число информационных разрядов 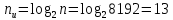 Число корректирующих разрядов 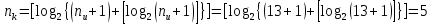 Общая длина кодовой комбинации 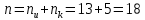 Порождающая матрица кода Хемминга: 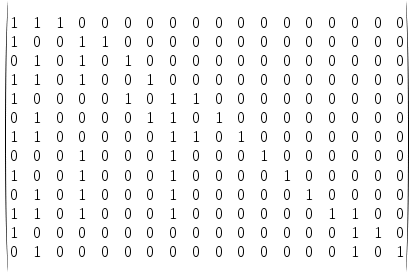 В соответствии с построением кода Хемминга, 1-й, 2-й, 4-й, 8-й и 16-й столбцы порождающей матрицы (то есть столбцы, номера которых есть степень 2) соответствуют корректирующим разрядам кода Хемминга. Остальные столбцы представляют собой единичную матрицу, по главной диагонали которой стоят 1, остальные элементы - 0. Корректирующие столбцы заполняются в соответствии с кодом Хемминга: b1 = b3+b5+b7+b9+b11+b13+b15+b17; b2 = b3+b6+b7+b10+b11+b14+b15+b18; b4 = b5+b6+b7+b12+b13+b14+b15; b8 = b9+b10+b11+b12+b13+b14+b15; b16=b17+b18 (цифры обозначают номера столбцов производящей матрицы; эти формулы применяются к каждой из 13 строк производящей матрицы). Суммы берутся по модулю 2, то есть если получается четная цифра (например, 2), берется 0, а если получается нечетная цифра (например, 3), то берется 1. Для получения линейно-группового кода порождающая матрица по правилам алгебры умножается на данный двоичный код. Так как в итоге должна получиться строка, состоящая только из цифр 0 и 1, произведение берется по модулю 2. 2. Привести пример 10 кодовых комбинаций.
3. Показать процесс исправления ошибки в заданном разряде k. Построим проверочную матрицу. В первой ее строке стоят 1 в тех столбцах, номера которых – нечетные числа 1, 3, 5, 7 и т.д. (то есть числа, в двоичной записи которых на последнем месте стоит 1). В остальных столбцах – 0. Во второй строке стоят 1 в столбцах с номерами 2, 3, 6, 7 и т.д. (то есть с номерами, в двоичной записи которых на втором месте справа стоят 1). В остальных столбцах – 0. В третьей строке стоят 1 в столбцах с номерами 4, 5, 6, 7, 12 и т.д. (то есть с номерами, в двоичной записи которых на третьем месте справа стоят 1). В остальных столбцах – 0. В четвертой строке стоят 1 в столбцах с номерами 8, 9, 10 и т.д. (то есть с номерами, в двоичной записи которых на четвертом месте справа стоят 1). В пятой строке стоят 1 в столбцах с номерами 16, 17, 18 (то есть с номерами, в двоичной записи которых на пятом месте справа стоят 1). Проверочная матрица: 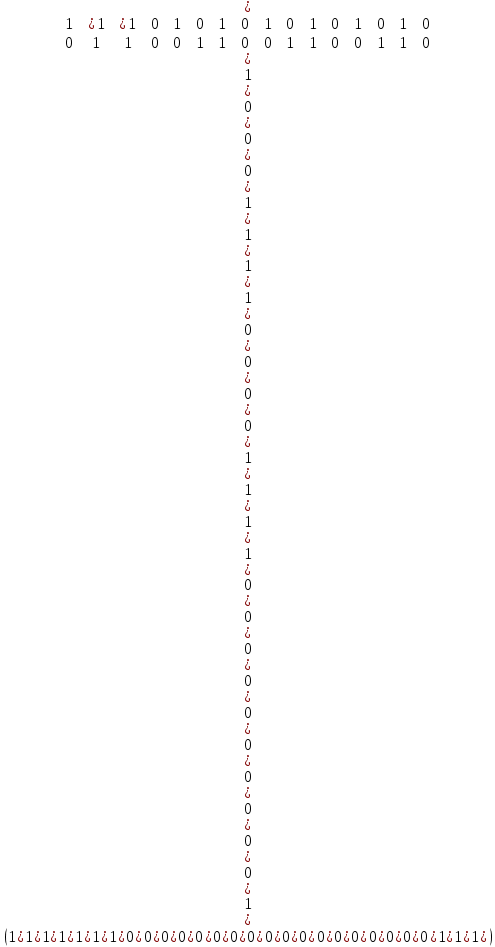 Пусть при передаче сообщения 100000000000000110 произошла ошибка в 3-м разряде, т.е. принято сообщение 101000000000000110. Тогда 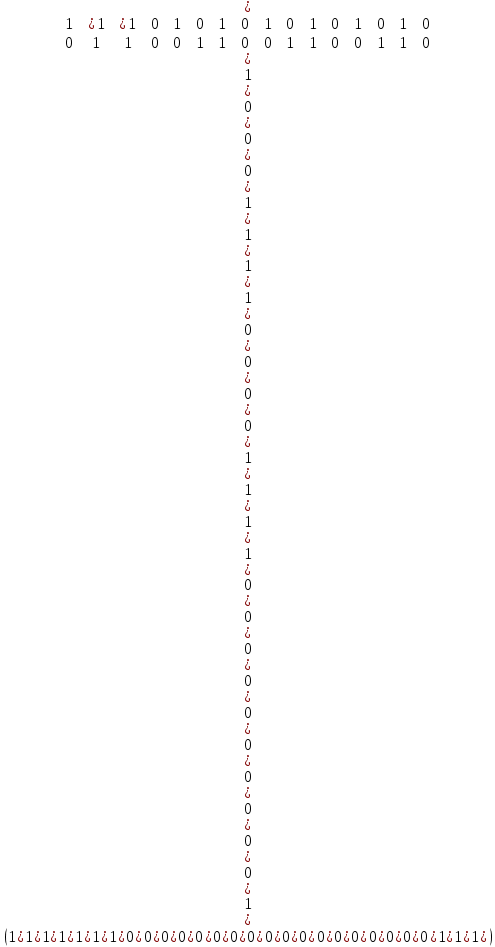 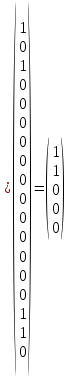 Двоичный номер ошибочного разряда 00011. Значит, ошибка допущена в 3-м разряде. Исправленное сообщение: 100000000000000110. |
