Лабораторная работа по физике 5. Лабораторная по физике. Лабораторная работа 5 Определение постоянных Ридберга и Планка по линиям спектра испускания водорода
 Скачать 174.27 Kb. Скачать 174.27 Kb.
|
|
Лабораторная работа №5 Определение постоянных Ридберга и Планка по линиям спектра испускания водорода. Цель работы: Ознакомление с устройством простейшего монохроматора, градуировка его шкалы по известному спектру газа и определение постоянных Ридберга и Планка по линиям спектра водорода. Теория Спектры излучения одноатомных газов состоят из ряда тонких линий, расположенных в инфракрасной, видимой и ультрафиолетовой частях спектра. Для атомарного водорода эти линии описываются формулой Бальмера-Ридберга (5.1) 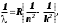 где - длина волны линии, R=1,09737107 м-1 - постоянная Ридберга, n - целое число, определяющее номер серии; n>k - целое число, определяющее номер линии внутри одной серии. При n=2 (k=3,4,5, ...) имеем так называемую серию Бальмера (5.2) где - длина волны линии, R=1,09737107 м-1 - постоянная Ридберга, n - целое число, определяющее номер серии; n>k - целое число, определяющее номер линии внутри одной серии. При n=2 (k=3,4,5, ...) имеем так называемую серию Бальмера (5.2)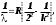 первые три линии которой лежат в видимой области (0,4<<0,75 мкм). Значения n=1 (k=2,3,4, ...) соответствуют “ультрафиолетовой” серии Лаймана. Остальные серии лежат в инфракрасной области спектра. первые три линии которой лежат в видимой области (0,4<<0,75 мкм). Значения n=1 (k=2,3,4, ...) соответствуют “ультрафиолетовой” серии Лаймана. Остальные серии лежат в инфракрасной области спектра. Полное решение квантово-механической задачи для микрообъекта массой m, имеющего потенциальную энергию U(x,y,z), дает стационарное уравнение Шредингера 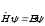 , где оператор энергии , где оператор энергии 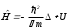 ; E -собственные значения полной энергии микрообъекта; - стационарная часть волновой функции, квадрат которой, определяемый как произведение волновой функции на комплексно с ней сопряженную *, связан с вероятностью dP нахождения микрообъекта массой m в объеме dV соотношением ; E -собственные значения полной энергии микрообъекта; - стационарная часть волновой функции, квадрат которой, определяемый как произведение волновой функции на комплексно с ней сопряженную *, связан с вероятностью dP нахождения микрообъекта массой m в объеме dV соотношением dP = 2dV= *dV; (5.3) - оператор Лапласа, U - потенциальная энергия микрообъекта, 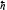 =h/2 - постоянная Планка (h = 6,6261910-34 Джс). =h/2 - постоянная Планка (h = 6,6261910-34 Джс). В атоме водорода потенциальная энергия электрона в поле протона равна (5.4) 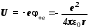 , где r- расстояние от электрона до положительного ядра атома. Подставляя (5.4) в (5.3), получим уравнение Шредингера для электрона в атоме водорода , где r- расстояние от электрона до положительного ядра атома. Подставляя (5.4) в (5.3), получим уравнение Шредингера для электрона в атоме водорода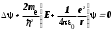 . (5.5) . (5.5)Решением этого уравнения в сферической системе координат являются известные собственные функции 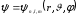 (5.6) с собственными значениями энергии электрона в атоме водорода (5.7) (5.6) с собственными значениями энергии электрона в атоме водорода (5.7)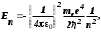 где главное квантовое число n (=1,2,3...) совпадает с номером уровня энергии En электрона; азимутальное квантовое число l может принимать n различных значений: l=0,1,2,...n-1; магнитное квантовое число m при данном l может принимать 2l+1 различных значений: m = -l, -l+1, -l+2,...-1, 0, +1,.., l-1, l. где главное квантовое число n (=1,2,3...) совпадает с номером уровня энергии En электрона; азимутальное квантовое число l может принимать n различных значений: l=0,1,2,...n-1; магнитное квантовое число m при данном l может принимать 2l+1 различных значений: m = -l, -l+1, -l+2,...-1, 0, +1,.., l-1, l.Cостояния с одинаковой энергией (одинаковым n, но разными l и/или m) называются вырожденными, а их число называется кратностью вырождения этого энергетического уровня. Каждому из n значений квантового числа l соответствуют 2l+1 значений квантового числа m. Следовательно, число различных состояний, соответствующих данному n, равно 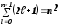 . .Полученная при решении уравнения Шредингера формула (5.7) совпадает с полученной Н.Бором в полуклассической планетарной модели водородоподобного атома. При создании этой модели, Бору пришлось вводить дополнительные предположения (постулаты Бора), допускающие движение электрона по определенным орбитам , но запрещающие излучение света при ускоренном движении по этим орбитам. Это противоречит как классической теории Максвелла, так и квантово-механической, отвергающей понятие “орбита” для электрона в атоме. Поэтому неудивительно, что все попытки обобщить теорию Бора на другие атомы оказались безуспешными. Найденные в результате решения уравнения Шредингера (5.5) волновые функции (5.6) позволяют найти вероятность нахождения электрона dP в объеме dV по формуле (5.3). Так, для основного состояния электрона в атоме водорода (n=1, l=0, m=0,так называемое “s”- состояние) (5.8) 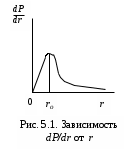 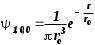 , где r0=40 , где r0=40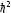 /me2(первый боровский радиус). Подставляя (5.8) в (5.3), и dV = 4r2dr, получим для плотности вероятности по r ( dP/dr) для "s" состояния выражение (5.9) /me2(первый боровский радиус). Подставляя (5.8) в (5.3), и dV = 4r2dr, получим для плотности вероятности по r ( dP/dr) для "s" состояния выражение (5.9) 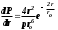 , график которого представлен на рис. 5.1. , график которого представлен на рис. 5.1.Видно, что никаких орбит для электрона решение уравнения Шредингера не дает. Можно говорить только о плотности нахождения электрона в зависимости от r. При этом максимум плотности вероятности для основного состояния соответствует r= r0, т.е. первой орбите в модели Н.Бора. Испускание кванта света с энергией 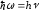 происходит при переходе электрона из состояния с большей энергией Ek в состояние с меньшей энергией En. Поэтому, принимая во внимание (5.7), можно записать (5.10) происходит при переходе электрона из состояния с большей энергией Ek в состояние с меньшей энергией En. Поэтому, принимая во внимание (5.7), можно записать (5.10)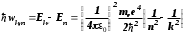 , где me - масса электрона, с- скорость света в вакууме . , где me - масса электрона, с- скорость света в вакууме .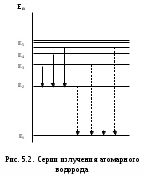 На рис. 5.2 горизонтальными линиями показаны уровни полной энергии электрона в атоме водорода, даваемые формулой (5.7) , а стрелками показаны электронные переходы, сопровождающиеся излучением квантов света в соответствии с формулой (5.1) в сериях излучения Бальмера (сплошные линии) и Лаймана (пунктир). Сравнивая (5.1) и (5.10), можно видеть, что они совпадают, если (5.11) 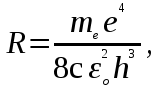 откуда для постоянной Планка имеем откуда для постоянной Планка имеем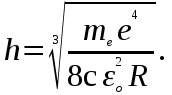 (5.12) (5.12)Постоянную Ридберга R вычисляют, используя определенные экспериментально длины волн первых трех линий серии Бальмера по формуле (5.13) 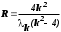 , легко получающейся из (5.2). Источник: методичка к лаб. Работе. , легко получающейся из (5.2). Источник: методичка к лаб. Работе.Лабораторная установка 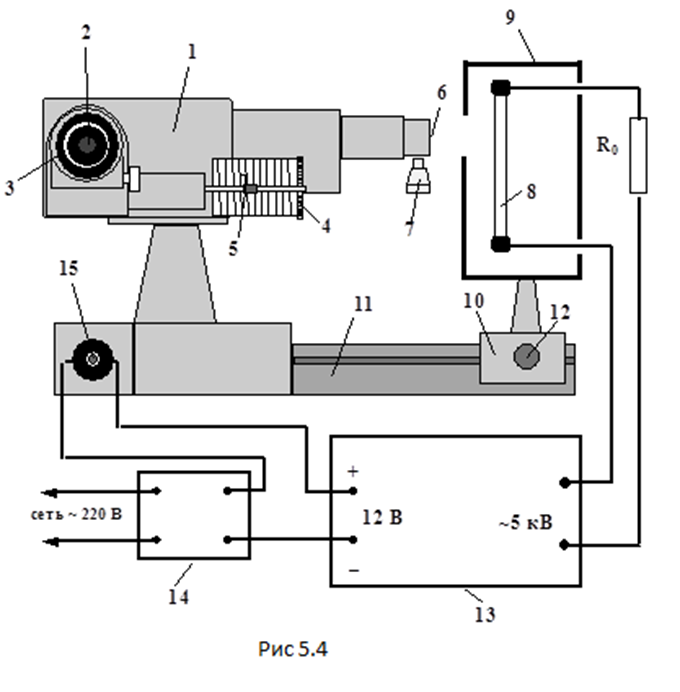 Блок-схема лабораторной установки (рис. 5.4) содержит монохроматор (1) УМ-2, используемый в режиме спектроскопа (для визуального наблюдения исследуемого спектра) и спектрометра (для одновременного измерения длин волн линий в спектре). С этой целью вместо выходной щели установлена зрительная труба 2 (окуляр), через которую можно наблюдать спектр в плоскости, где ранее находилась эта щель. В центре поля зрения окуляра находится измерительный нож, лежащий в плоскости изображения спектра. Шайба 3 служит для наводки спектра и измерительной кромки ножа "на резкость". С помощью барабана 4 можно поворачивать призму монохроматора и выводить желаемую линию спектра в центр поля зрения окуляра. Положение барабана контролируется указателем 5. Ширина входной щели 6 монохроматора устанавливается микрометрическим барабаном 7. Трубка 8 с исследуемым газом закреплена в светозащитном кожухе 9 на рейтере 10. Рейтер устанавливается на рельсе 11 окном к щели 6 и фиксируется винтом 12. На трубку подается переменное напряжение 10 кГц от частотного преобразователя 13, питающегося от выпрямителя 14. При подаче высокого напряжения на электроды трубки 8 возникает газовый разряд, обусловленный протеканием ионного и электронного токов между электродами. В результате столкновений между ионами, атомами и электронами происходит возбуждение исследуемых атомов, а при обратных переходах - излучение наблюдаемых спектральных линий. Одновременно идет ионная и электронная бомбардировка электродов трубки, они нагреваются и выделяют посторонние растворенные в электродах газы, загрязняя исследуемый. Кроме этого, при длительной эксплуатации трубки происходит распыление материала электродов на ее стенки, что также приводит к соответствующим искажениям в спектре. Поэтому в настоящей работе для повышения длительности эксплуатации газовых трубок введено ограничивающее протекающий через трубку ток сопротивление R0, а подача высокого напряжения на трубку происходит только в момент измерения нажатием кнопки 15. Рабочая формула 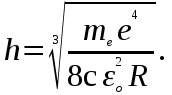 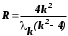 (Вывод см. в пункте «Теория») (Вывод см. в пункте «Теория»)Расчеты и измерения
Вычисление погрешности 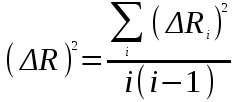 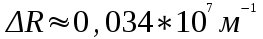 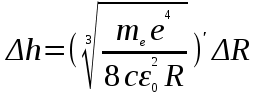 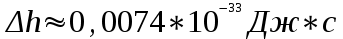 Результат 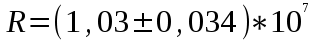 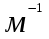 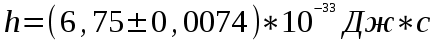 Контрольные вопросы Постулаты Н.Бора для атома Н и критика модели Бора в свете соотношения Гайзенберга. 1)Атом и атомные системы могут длительно пребывать только в особенных стационарных или квантовых состояниях, каждому из которых отвечает определенная энергия. В стационарном состоянии атом не излучает электромагнитных волн. 2)Излучение света происходит при переходе электрона из стационарного состояния с большей энергией в стационарное состояние с меньшей энергией. Энергия излученного фотона равна разности энергий стационарных состояний. Из них выводится, что постоянная Ридберга равна энергии связи электрона в атоме водорода в основном состоянии, т.е. минимальной энергии, необходимой для ионизации атома водорода в низшем (стабильном) энергетическом состоянии. Согласно принципу неопределённости Гейзенберга у частицы не могут быть одновременно точно измерены положение и скорость (импульс). 2. Чем отличаются серии Бальмера и Лаймана от других серий, наблюдаемых в спектре атомарного водорода? При n1 = 1 получается серия Лаймана, лежащая в далёкой ультрафиолетовой области спектра, при n1 = 2 — серия Бальмера, линии которой расположены в видимой и близкой ультрафиолетовой областях. Серии Пашена (n1 = 3), Брэкета (n1 = 4), Пфаунда (n1 = 5), Хамфри (n1 = 6) лежат в инфракрасной области спектра. 3. Каковы результаты решения стационарного уравнения Шредингера для атома Н? Уравнение Шредингера, примененное к атому водорода, позволяет получить результаты боровской теории атома водорода без привлечения постулатов Бора и условия квантования.  Эта формула совпадает с полученной Бором формулой для энергии стационарных состояний атома водорода. Эта формула совпадает с полученной Бором формулой для энергии стационарных состояний атома водорода.4. Что такое кратность вырождения данного энергетического состояния? Является ли основное состояние энергии электрона в атоме водорода вырожденным? 5. Какую величину позволяет вычислить знание волновой функции ? Вероятность нахождения микрообъекта массой m в некотором объеме V либо вероятность его нахождения в момент t в некоторой точке x,x,z. 6. Что такое правило отбора и как оно объясняется? Как найти импульс фотона? Правила отбора ограничивают число принципиально возможных переходов электронов в атоме, связанных с излучением и поглощением света. Эти правила являются следствием законов сохранения. 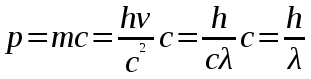 , где h – постоянная Планка, c – скорость света в вакууме, v – частота излучения, - длина волны. , где h – постоянная Планка, c – скорость света в вакууме, v – частота излучения, - длина волны.7. Что такое дисперсия вещества и где она полезно используется в монохроматоре? Дисперсия вещества определяется интенсивностью разложения света данным веществом. Дисперсией света называется зависимость показателя преломления n вещества от частоты света или зависимость фазовой скорости световых волн от их частоты. Дисперсия влияет на способность дифракционной решетки отклонять излучения с различной длиной волн на разные углы. 8. Зачем нужно иметь калибровочную кривую для данного монохроматора? 9. Как объяснить свечение газовой трубки при подаче на нее высокого напряжения? При подаче высокого напряжения кинетическая энергия ионов и электронов резко возрастает, газ ионизируется, следствием чего и является свечение газа. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 ,
,
 ,
, ,
,