Линейный оптимальный регулятор. Фильтр Калмана – Бьюси. Моделирование посадки беспилотного аппарата вертикального взлета и посад. Лабораторная работа 5 по предмету Теория случайных процессов Кафедра 301 На тему
 Скачать 1.26 Mb. Скачать 1.26 Mb.
|
|
Московский Авиационный Институт (Национальный Исследовательский Университет) Лабораторная работа №5 по предмету «Теория случайных процессов» Кафедра 301 На тему: «Линейный оптимальный регулятор. Фильтр Калмана – Бьюси. Моделирование посадки беспилотного аппарата вертикального взлета и посадки на корабль в условиях морского волнения» Вариант № 1 Преподаватель: Кудрявцев П.С. Студент: Антипенко Н.С. Группа: М3О-301С-19 Москва, 2021 Enter task variant Var=1 Wave model (0 - no wave, 1 - determined sin wave, 2 - random wave) IndWave= IndWave = 2 Ship model matrix eigenvalues ans = 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i -0.6000 + 1.2115i -0.6000 - 1.2115i 0.0000 + 0.0000i Wind gust model (0 - no wind, 1 - determined gust, 2 - random wind) IndWind= IndWind = 2 Matrix Aair eigenvalues ans = 0.0000 + 0.0000i 0.0000 + 0.0000i -0.3593 + 0.0000i 0.0982 + 0.2477i 0.0982 - 0.2477i -0.0201 + 0.0000i Make VTOL and Ship model analysis. Then press any key  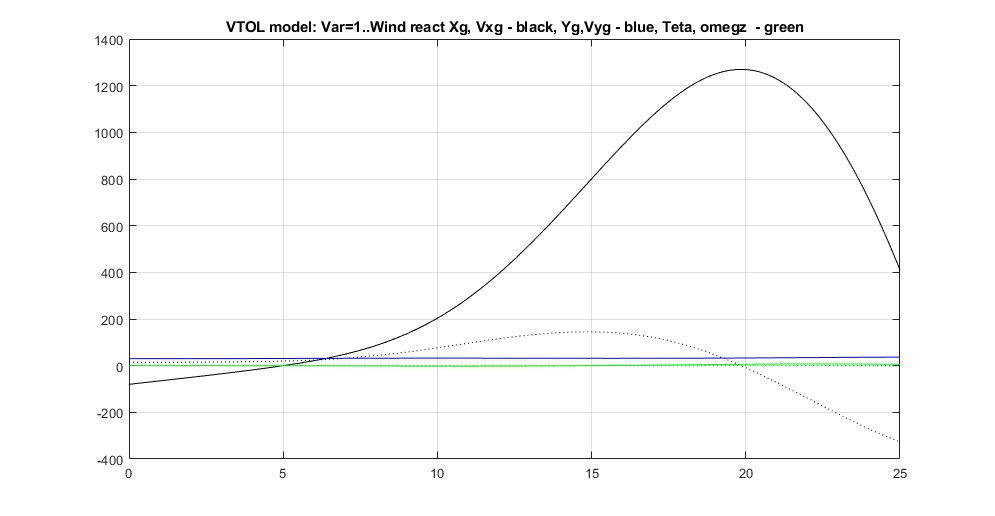 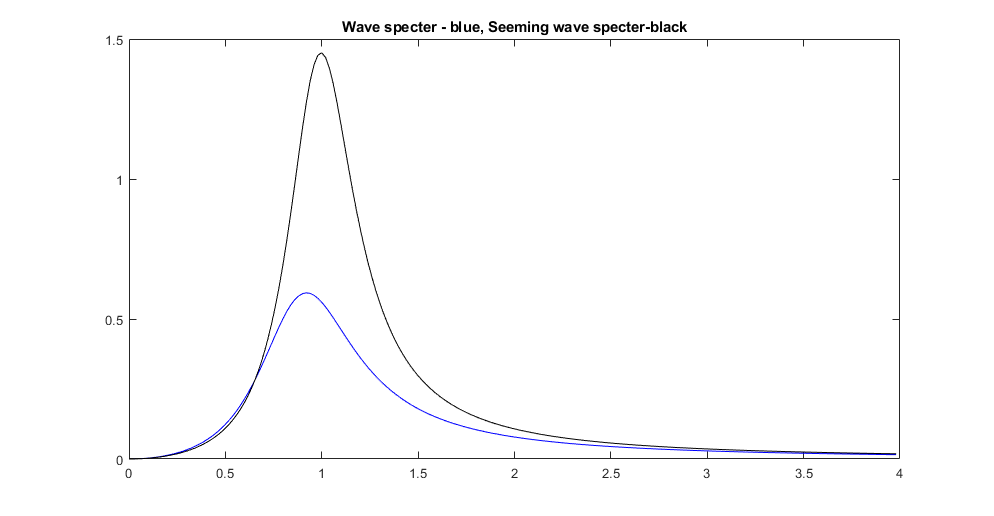  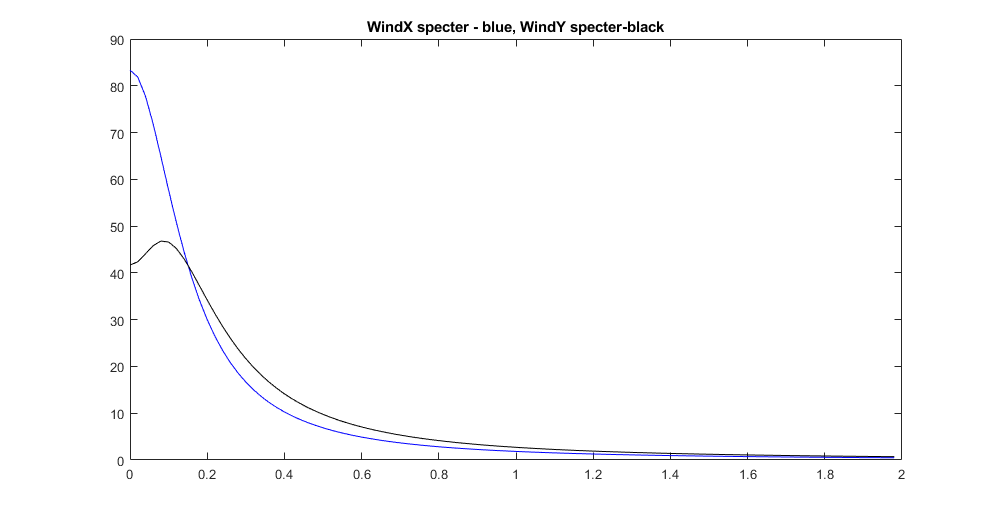 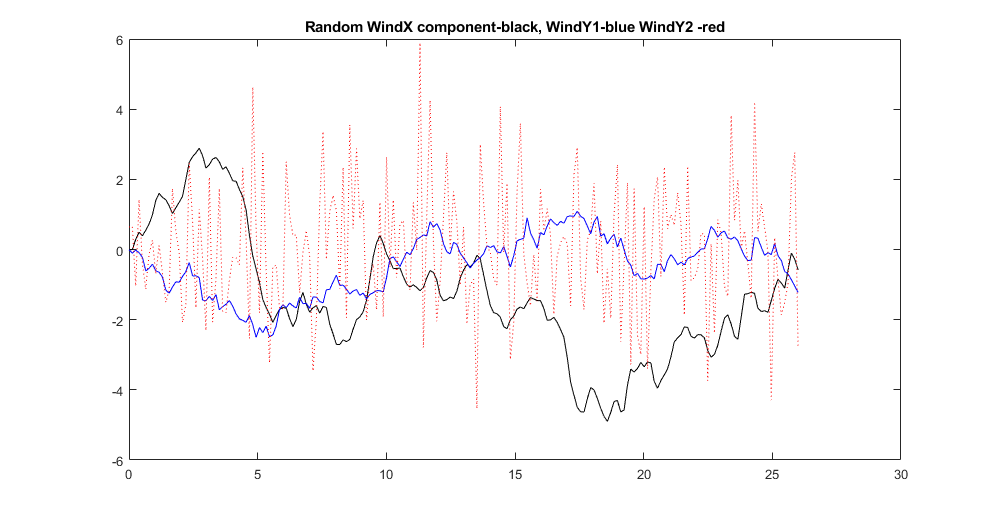 VTOL controllability matrix rank Frnk = 6 VTOL observability matrix rank Outputs: Tet and d/dt(Tet) H_TetdTetrnk = 3 VTOL observability matrix rank Outputs: Vx, Vy, Tet and d/dt(Tet) H_VxVyTetdTetrnk = 4 H_Xa_Ya_Wza = 6 VTOL observability matrix rank Outputs: Xa,Ya,Vx,Vy,Tet and d/dt(Tet) H_airrnk = 6 mev - error of Riccati equation desicion; Kfd - feedback matrix; Vr - positive Riccati matrix rnev = 1.2208e-15 Kfd = -0.6225 -0.0003 0.0933 -0.4750 -0.0023 -0.2595 -0.0007 0.0949 -0.0041 -0.0005 0.7589 0.0096 -0.1508 0.0001 2.7541 -0.1593 0.0053 1.2489 Vr = 1.9929 -0.0000 -1.2087 0.5044 -0.0009 -0.3283 -0.0000 0.8018 -0.0017 0.0001 0.1145 0.0002 -1.2087 -0.0017 35.5107 -1.2356 -0.0050 5.9941 0.5044 0.0001 -1.2356 0.4037 -0.0007 -0.3468 -0.0009 0.1145 -0.0050 -0.0007 0.9156 0.0116 -0.3283 0.0002 5.9941 -0.3468 0.0116 2.7181 Closed system matrix eigenvalues ans = -6.8746 + 0.0000i -3.3562 + 1.4481i -3.3562 - 1.4481i -2.0652 + 0.9437i -2.0652 - 0.9437i -0.1270 + 0.0000i Examine close-loop system with linear optimal controller. Make conclusions and press any key There are not wave and wind! Landing Mode IndWind = 0 IndWave = 0 Land ship time tlnd = 17.2581 Parameters ship and VTOL aircraft in land moment before engine stop. Tetair and Psi_sh deg= Tetair_lndDgr = 0.0355 Psish_lndDgr = 0 Xair_lnd = 34.5075 Xsh_lnd = 34.5163 Vertical Yair and Ysh movement Yair_lnd = 3.4159 Ysh_lnd = 4 Vxair and V_sh= Vxair_lnd = 2.0000 V_sh = 2 Vay and VYsh vertical speeds Vyair_lnd = -0.4339 VYsh_lnd = 0 Wzair and Wzsh angle speeds Wzair_lnd = -1.3040e-05 Wzsh_lnd = 0 Make examination jexam=1,2,3 results. Then press any key  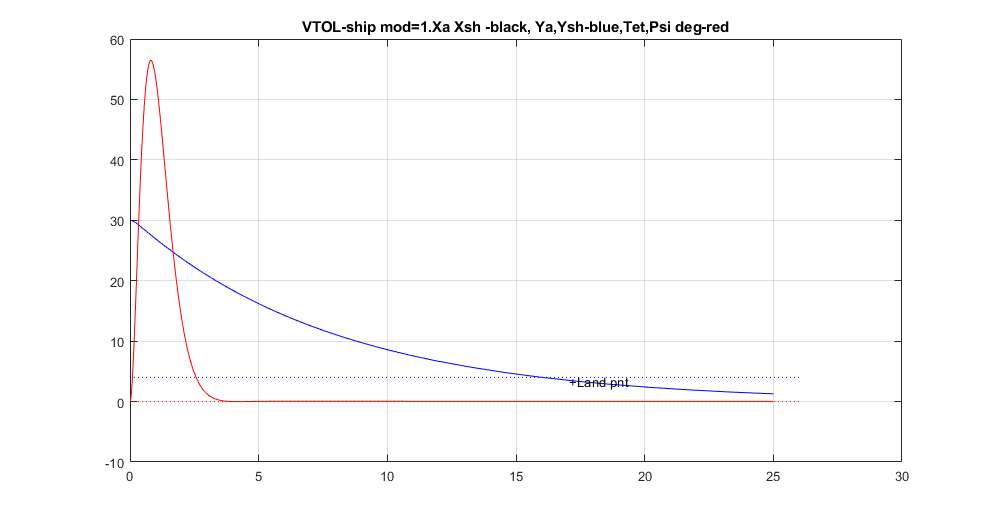 There are regular wave and wind Landing Mode IndWind = 1 IndWave = 1 Land ship time tlnd = 8.9309 Parameters ship and VTOL aircraft in land moment before engine stop. Tetair and Psi_sh deg= Tetair_lndDgr = -3.5122 Psish_lndDgr = -3.6770 Xair_lnd = 12.5529 Xsh_lnd = 11.7738 Vertical Yair and Ysh movement Yair_lnd = 5.1330 Ysh_lnd = 5.3269 Vxair and V_sh= Vxair_lnd = 0.1629 V_sh = 2 Vay and VYsh vertical speeds Vyair_lnd = 13.8014 VYsh_lnd = 14.5518 Wzair and Wzsh angle speeds Wzair_lnd = -0.5153 Wzsh_lnd = -0.5113 Make examination jexam=1,2,3 results. Then press any key 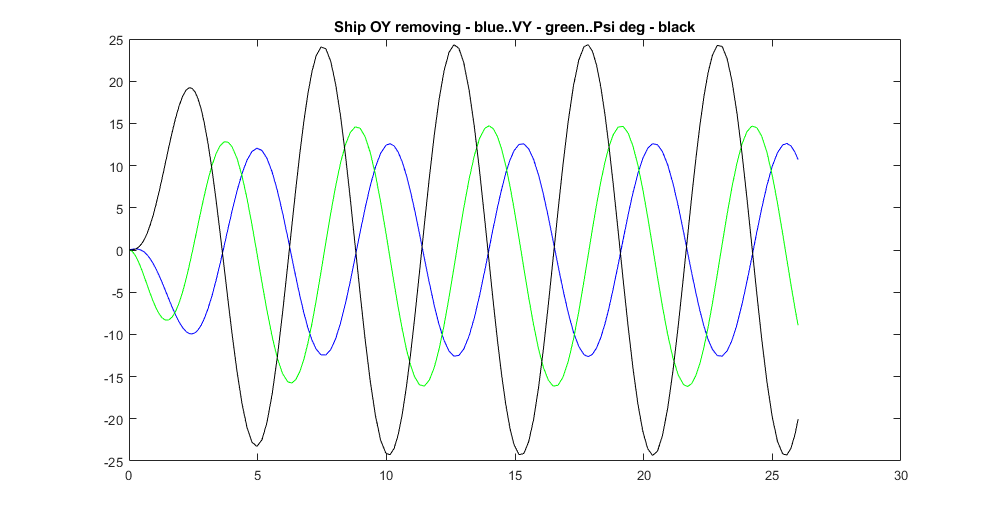  There are random wave and wind Landing Mode IndWind = 2 IndWave = 2 Land ship time tlnd = 8.8183 Parameters ship and VTOL aircraft in land moment before engine stop. Tetair and Psi_sh deg= Tetair_lndDgr = -3.1706 Psish_lndDgr = 0.2236 Xair_lnd = 12.9619 Xsh_lnd = 11.7901 Vertical Yair and Ysh movement Yair_lnd = 3.3317 Ysh_lnd = 3.3318 Vxair and V_sh= Vxair_lnd = -0.1797 V_sh = 2 Vay and VYsh vertical speeds Vyair_lnd = 12.4858 VYsh_lnd = 13.6116 Wzair and Wzsh angle speeds Wzair_lnd = -0.3720 Wzsh_lnd = -0.4833 Make examination jexam=1,2,3 results. Then press any key 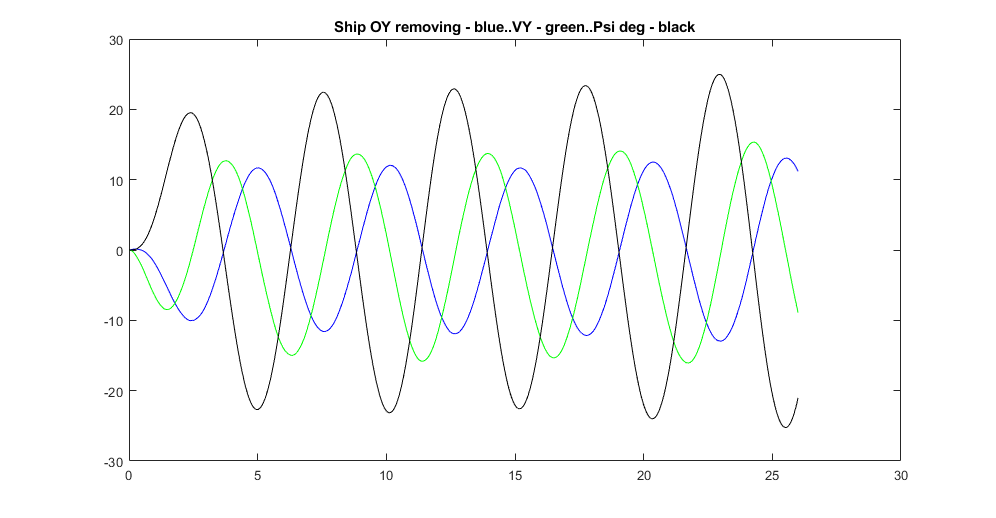 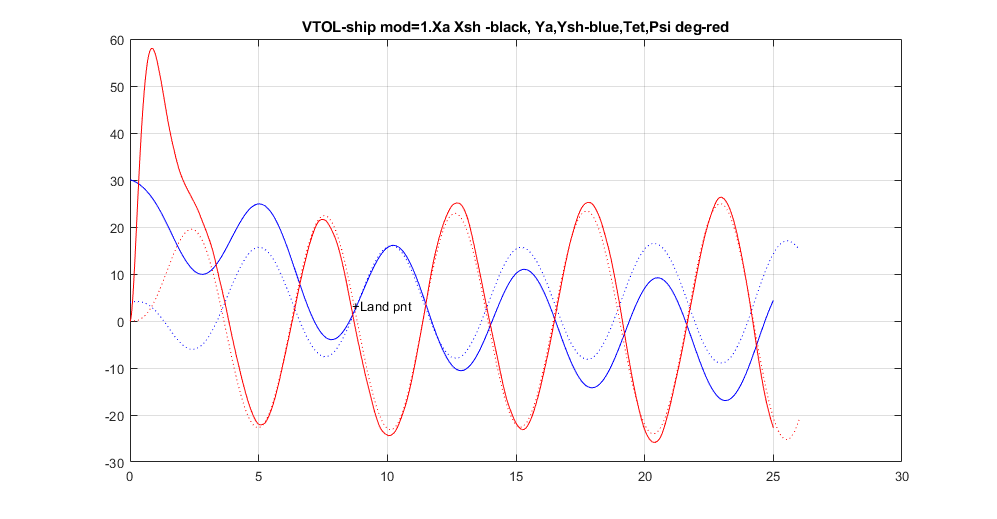 Gwdklm = 1.0000 0 0 0 0 0 0 0 0 1.0000 0 0 0 0 0 0 0 0 1.0000 0 0 0 0 0 0 0 0 1.0000 0 0 0 0 0 0 0 0 1.0000 0 0 0 0 0 0 0 0 1.0000 0 0 0 0 0 0 0 0 2.7386 0 0 0 0 0 0 0 0 1.0024 0 0 0 0 0 0 0 1.6771 Ra0 = 6.2500 0 0 0 0.2500 0 0 0 0.0100 KlmSysa = A = x1 x2 x3 x4 x5 x6 x7 x8 x9 x1 0 0 0 1 0 0 0.05 0 0 x2 0 0 0 0 1 0 0 0 -0.05 x3 0 0 0 0 0 1 0 0 0.1 x4 0 0 -9.81 -0.0201 0 0.0159 0.1 0 0 x5 0 0 0 0 -0.0201 0.1194 0 -0.2 -0.01 x6 0 0 0 0.0026 0.0203 -0.1427 0.03 0.002 0.08 x7 0 0 0 0 0 0 -0.15 0 0 x8 0 0 0 0 0 0 0 -0.15 0 x9 0 0 0 0 0 0 0 -0.15 -0.15 B = u1 u2 u3 u4 u5 u6 u7 u8 u9 u10 u11 x1 0 0 0 1 0 0 0 0 0 0 0 x2 0 0 0 0 1 0 0 0 0 0 0 x3 0 0 0 0 0 1 0 0 0 0 0 x4 -8.2 0 0 0 0 0 1 0 0 0 0 x5 0 9.2 0 0 0 0 0 1 0 0 0 x6 -1.6 0 5.1 0 0 0 0 0 1 0 0 x7 0 0 0 0 0 0 0 0 0 2.739 0 x8 0 0 0 0 0 0 0 0 0 0 1.002 x9 0 0 0 0 0 0 0 0 0 0 1.677 C = x1 x2 x3 x4 x5 x6 x7 x8 x9 y1 1 0 0 0 0 0 0 0 0 y2 0 1 0 0 0 0 0 0 0 y3 0 0 0 0 0 1 0 0 0 D = u1 u2 u3 u4 u5 u6 u7 u8 u9 u10 u11 y1 0 0 0 0 0 0 0 0 0 0 0 y2 0 0 0 0 0 0 0 0 0 0 0 y3 0 0 0 0 0 0 0 0 0 0 0 Continuous-time state-space model. Aklmest = A = x1_e x2_e x3_e x4_e x5_e x6_e x7_e x8_e x9_e x1_e -2.097 -0.6659 0 1 0 1.149 0.05 0 0 x2_e -0.02664 -1.951 0 0 1 0.3291 0 0 -0.05 x3_e 0.1112 0.1687 0 0 0 -1.06 0 0 0.1 x4_e -2.074 -1.501 -9.81 -0.0201 0 8.23 0.1 0 0 x5_e -0.03883 -1.372 0 0 -0.0201 0.6358 0 -0.2 -0.01 x6_e 0.001839 0.01316 0 0.0026 0.0203 -2.062 0.03 0.002 0.08 x7_e -0.3699 -0.7044 0 0 0 -14.44 -0.15 0 0 x8_e 0.1376 0.621 0 0 0 -5.777 0 -0.15 0 x9_e 0.1626 0.8427 0 0 0 -8.812 0 -0.15 -0.15 B = u1 u2 u3 y1 y2 y3 x1_e 0 0 0 2.097 0.6659 -1.149 x2_e 0 0 0 0.02664 1.951 -0.3291 x3_e 0 0 0 -0.1112 -0.1687 2.06 x4_e -8.2 0 0 2.074 1.501 -8.214 x5_e 0 9.2 0 0.03883 1.372 -0.5164 x6_e -1.6 0 5.1 -0.001839 -0.01316 1.919 x7_e 0 0 0 0.3699 0.7044 14.44 x8_e 0 0 0 -0.1376 -0.621 5.777 x9_e 0 0 0 -0.1626 -0.8427 8.812 C = x1_e x2_e x3_e x4_e x5_e x6_e x7_e x8_e x9_e y1_e 1 0 0 0 0 0 0 0 0 y2_e 0 1 0 0 0 0 0 0 0 y3_e 0 0 0 0 0 1 0 0 0 x1_e 1 0 0 0 0 0 0 0 0 x2_e 0 1 0 0 0 0 0 0 0 x3_e 0 0 1 0 0 0 0 0 0 x4_e 0 0 0 1 0 0 0 0 0 x5_e 0 0 0 0 1 0 0 0 0 x6_e 0 0 0 0 0 1 0 0 0 x7_e 0 0 0 0 0 0 1 0 0 x8_e 0 0 0 0 0 0 0 1 0 x9_e 0 0 0 0 0 0 0 0 1 D = u1 u2 u3 y1 y2 y3 y1_e 0 0 0 0 0 0 y2_e 0 0 0 0 0 0 y3_e 0 0 0 0 0 0 x1_e 0 0 0 0 0 0 x2_e 0 0 0 0 0 0 x3_e 0 0 0 0 0 0 x4_e 0 0 0 0 0 0 x5_e 0 0 0 0 0 0 x6_e 0 0 0 0 0 0 x7_e 0 0 0 0 0 0 x8_e 0 0 0 0 0 0 x9_e 0 0 0 0 0 0 Input groups: Name Channels KnownInput 1,2,3 Measurement 4,5,6 Output groups: Name Channels OutputEstimate 1,2,3 StateEstimate 4,5,6,7,8,9,10,11,12 Continuous-time state-space model. Laklm = 2.0965 0.6659 -1.1493 0.0266 1.9509 -0.3291 -0.1112 -0.1687 2.0600 2.0739 1.5012 -8.2141 0.0388 1.3720 -0.5164 -0.0018 -0.0132 1.9188 0.3699 0.7044 14.4435 -0.1376 -0.6210 5.7768 -0.1626 -0.8427 8.8119 Erraklm = 13.1032 0.1665 -0.6949 12.9619 0.2427 -0.0115 2.3116 -0.8602 -1.0165 0.1665 0.4877 -0.0422 0.3753 0.3430 -0.0033 0.1761 -0.1552 -0.2107 -0.6949 -0.0422 0.1357 -1.3795 -0.0643 0.0206 -0.3202 0.2755 0.3781 12.9619 0.3753 -1.3795 20.5112 0.5526 -0.0821 4.4052 -2.0343 -2.5632 0.2427 0.3430 -0.0643 0.5526 0.6339 -0.0052 0.2932 -0.2559 -0.3520 -0.0115 -0.0033 0.0206 -0.0821 -0.0052 0.0192 0.1444 0.0578 0.0881 2.3116 0.1761 -0.3202 4.4052 0.2932 0.1444 14.7827 -1.3563 -1.8165 -0.8602 -0.1552 0.2755 -2.0343 -0.2559 0.0578 -1.3563 1.5210 2.2439 -1.0165 -0.2107 0.3781 -2.5632 -0.3520 0.0881 -1.8165 2.2439 3.4000 VTOL Kalman Press key Observability matrix rank Hr = 17 R0 Choleckii factorization R0chl = 2.4698 0.0081 0 0.1620 0 0.1215 0.0162 0.0040 0 0.7000 0 -0.0019 0 -0.0014 -0.0002 -0.0000 0 0 0.1000 0.1000 0 0 0 0 0 0 0 0.5690 0.3515 -0.0346 -0.0046 -0.0012 0 0 0 0 0.7046 0.0172 0.0023 0.0006 0 0 0 0 0 1.5439 -0.0014 -0.0004 0 0 0 0 0 0 1.0487 -0.0001 0 0 0 0 0 0 0 0.2000 open loop system VTOL,Ship,Wave,Wind eigenvalues ans = 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i -0.3593 + 0.0000i 0.0982 + 0.2477i 0.0982 - 0.2477i -0.0201 + 0.0000i -0.6000 + 1.2115i -0.6000 - 1.2115i -0.2040 + 0.9716i -0.2040 - 0.9716i -0.1500 + 0.0000i -0.1500 + 0.0000i -0.1500 + 0.0000i Kalman filter coefficients Lklm = 0.7246 0.0292 -1.2752 2.1782 -0.2798 0.5161 0.1338 -0.3418 -0.0078 1.5086 -0.4905 0.0573 0.1885 0.0618 0.0858 0.1568 0.0054 -0.0659 1.7277 -0.2278 0.0585 -0.1394 -0.0184 0.3520 0.1999 0.3555 -6.1631 2.4953 -0.5104 1.4985 0.1381 -1.1080 -0.0128 0.9104 -0.6542 0.1189 0.1527 0.0778 0.1322 0.1414 0.0041 -0.0090 1.7134 -0.0380 0.0256 -0.0151 -0.0044 0.3961 0.8318 -0.0778 1.6033 -1.7227 0.3838 0.1709 0.3520 -0.5484 -0.0967 1.2503 -2.0431 0.7803 -2.7011 -0.0281 0.3069 1.5631 -0.0061 0.0027 -0.0721 0.0630 -0.0197 -0.0046 -0.0912 0.0562 0.2104 0.0571 -0.0070 -0.1573 -0.0456 -0.0246 -0.0328 0.0056 -0.0584 0.7204 -0.8240 0.7517 0.3351 0.0053 -3.1228 0.6218 0.0076 -0.0218 0.1617 -0.0750 0.1269 0.0031 0.0126 -0.1998 -0.0123 0.1850 13.0449 1.0321 0.0081 0.4988 0.0799 3.3300 0.0277 -0.3043 5.3583 -0.5109 0.0641 -0.2857 -0.0791 1.0897 0.0417 -0.4147 8.2016 -0.7012 0.0895 -0.3895 -0.1132 1.6942 -0.0111 -0.0343 0.0943 0.0447 0.1441 -0.0202 0.0946 -0.1732 0.0239 0.0397 0.1709 -0.1149 -0.0433 0.0324 0.0190 -0.0710 Dispersion estimation xklm matrix Errklm = Columns 1 through 11 5.4484 0.0288 -0.0988 2.6688 0.0177 0.0090 4.4431 -0.2334 -0.0164 1.2128 -0.1584 0.0288 0.7390 -0.0322 0.1782 0.4458 -0.0043 -0.0215 0.6107 0.0012 0.0322 0.3518 -0.0988 -0.0322 0.0641 -0.3697 -0.0428 0.0150 -0.0479 -0.0229 0.0005 -0.0369 -0.0227 2.6688 0.1782 -0.3697 4.6027 0.2108 -0.0367 1.8542 -0.0044 -0.0141 0.9463 0.0509 0.0177 0.4458 -0.0428 0.2108 0.6873 -0.0054 -0.0439 0.3274 0.0043 0.0280 0.5425 0.0090 -0.0043 0.0150 -0.0367 -0.0054 0.0168 -0.0012 -0.0126 -0.0001 -0.0016 -0.0007 4.4431 -0.0215 -0.0479 1.8542 -0.0439 -0.0012 4.6378 0.0851 -0.0320 1.1945 -0.4644 -0.2334 0.6107 -0.0229 -0.0044 0.3274 -0.0126 0.0851 2.1294 0.0008 0.0919 -0.0063 -0.0164 0.0012 0.0005 -0.0141 0.0043 -0.0001 -0.0320 0.0008 0.0094 -0.0012 0.1049 1.2128 0.0322 -0.0369 0.9463 0.0280 -0.0016 1.1945 0.0919 -0.0012 0.9423 0.0557 -0.1584 0.3518 -0.0227 0.0509 0.5425 -0.0007 -0.4644 -0.0063 0.1049 0.0557 3.9799 0.0155 -0.0105 0.0009 0.0056 -0.0109 0.0009 0.0124 -0.0742 -0.0023 -0.0040 -0.0250 0.5278 0.0904 -0.0917 1.2121 0.1790 0.1408 0.0291 -0.1210 -0.0028 0.0186 0.0915 -0.1194 -0.1486 0.1740 -0.7115 -0.2282 0.0485 -0.0130 -0.0861 -0.0012 -0.0341 -0.1423 -0.1387 -0.2024 0.2514 -0.9603 -0.3184 0.0750 -0.0029 -0.1176 -0.0020 -0.0380 -0.1955 -0.0548 -0.0170 0.0078 -0.0996 -0.0195 0.0014 -0.0961 -0.1153 0.0150 -0.0478 -0.1232 0.1105 0.0200 -0.0009 0.0475 0.0153 0.0006 0.1493 0.0698 -0.0172 -0.0375 -0.0066 Columns 12 through 17 0.0155 0.5278 -0.1194 -0.1387 -0.0548 0.1105 -0.0105 0.0904 -0.1486 -0.2024 -0.0170 0.0200 0.0009 -0.0917 0.1740 0.2514 0.0078 -0.0009 0.0056 1.2121 -0.7115 -0.9603 -0.0996 0.0475 -0.0109 0.1790 -0.2282 -0.3184 -0.0195 0.0153 0.0009 0.1408 0.0485 0.0750 0.0014 0.0006 0.0124 0.0291 -0.0130 -0.0029 -0.0961 0.1493 -0.0742 -0.1210 -0.0861 -0.1176 -0.1153 0.0698 -0.0023 -0.0028 -0.0012 -0.0020 0.0150 -0.0172 -0.0040 0.0186 -0.0341 -0.0380 -0.0478 -0.0375 -0.0250 0.0915 -0.1423 -0.1955 -0.1232 -0.0066 0.0088 0.0077 0.0046 0.0068 0.0084 0.0032 0.0077 13.6383 -0.9909 -1.3679 -0.0139 0.0160 0.0046 -0.9909 1.3489 2.0255 0.0140 -0.0027 0.0068 -1.3679 2.0255 3.1177 0.0185 -0.0026 0.0084 -0.0139 0.0140 0.0185 0.2728 -0.1165 0.0032 0.0160 -0.0027 -0.0026 -0.1165 0.3185 Closed Kalman filter eigenvalues ans = -2.0744 + 2.4410i -2.0744 - 2.4410i -2.9416 + 0.0000i -1.6950 + 0.9542i -1.6950 - 0.9542i -1.3817 + 0.2554i -1.3817 - 0.2554i -0.2770 + 0.9276i -0.2770 - 0.9276i -0.8351 + 0.9327i -0.8351 - 0.9327i -0.7768 + 0.5568i -0.7768 - 0.5568i -0.3810 + 0.2489i -0.3810 - 0.2489i -0.4978 + 0.0000i -0.0707 + 0.0000i Estimate Kalman filter construction results. Then modelling Close in VTOL-Ship with random wave and wind. Press any key 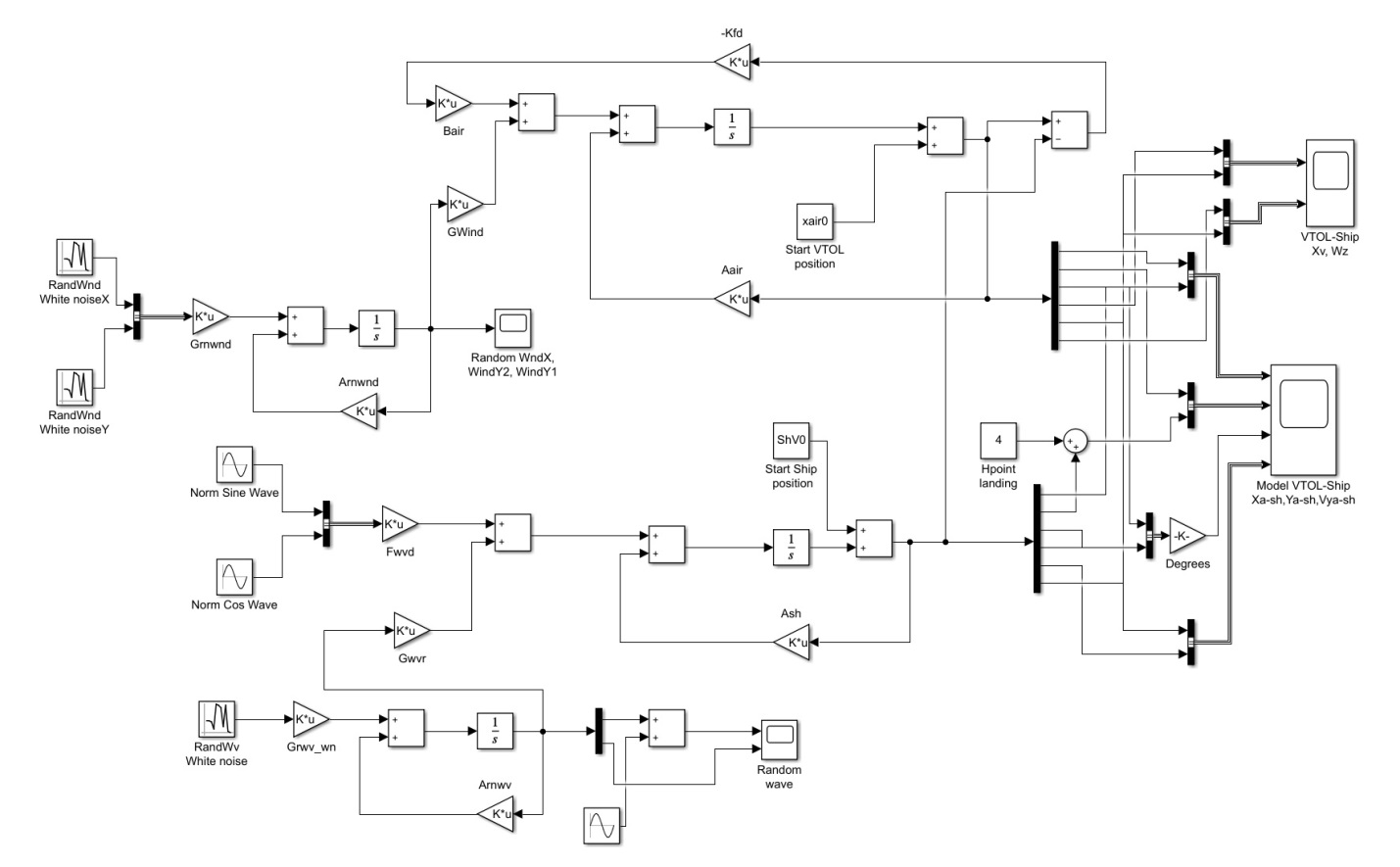 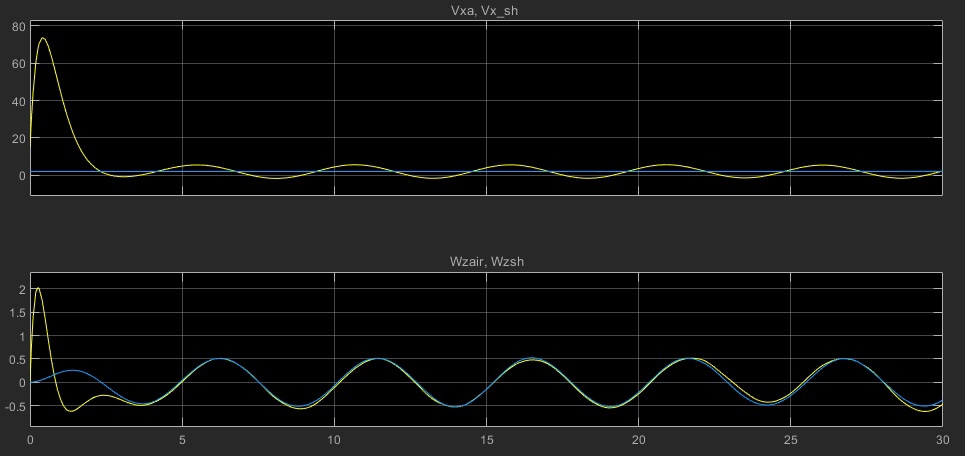 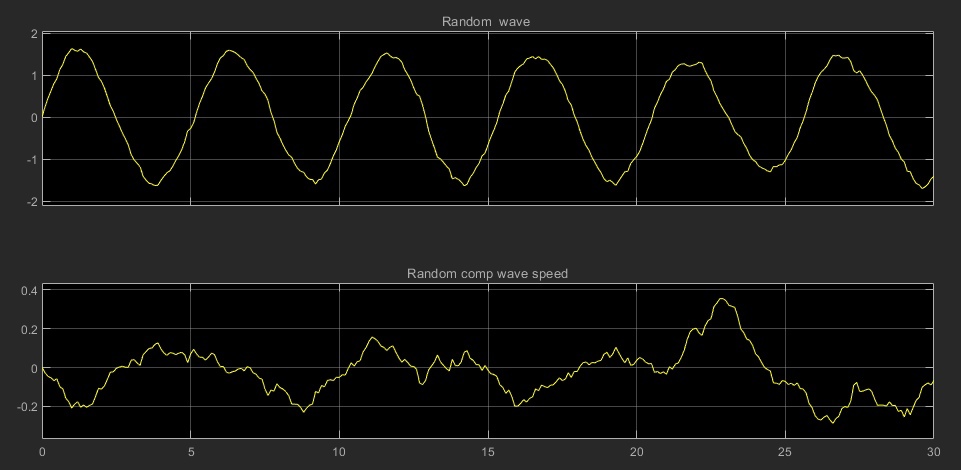 Examine Simulink close in model results. Then press any key Modelling close in model with Kalman filter 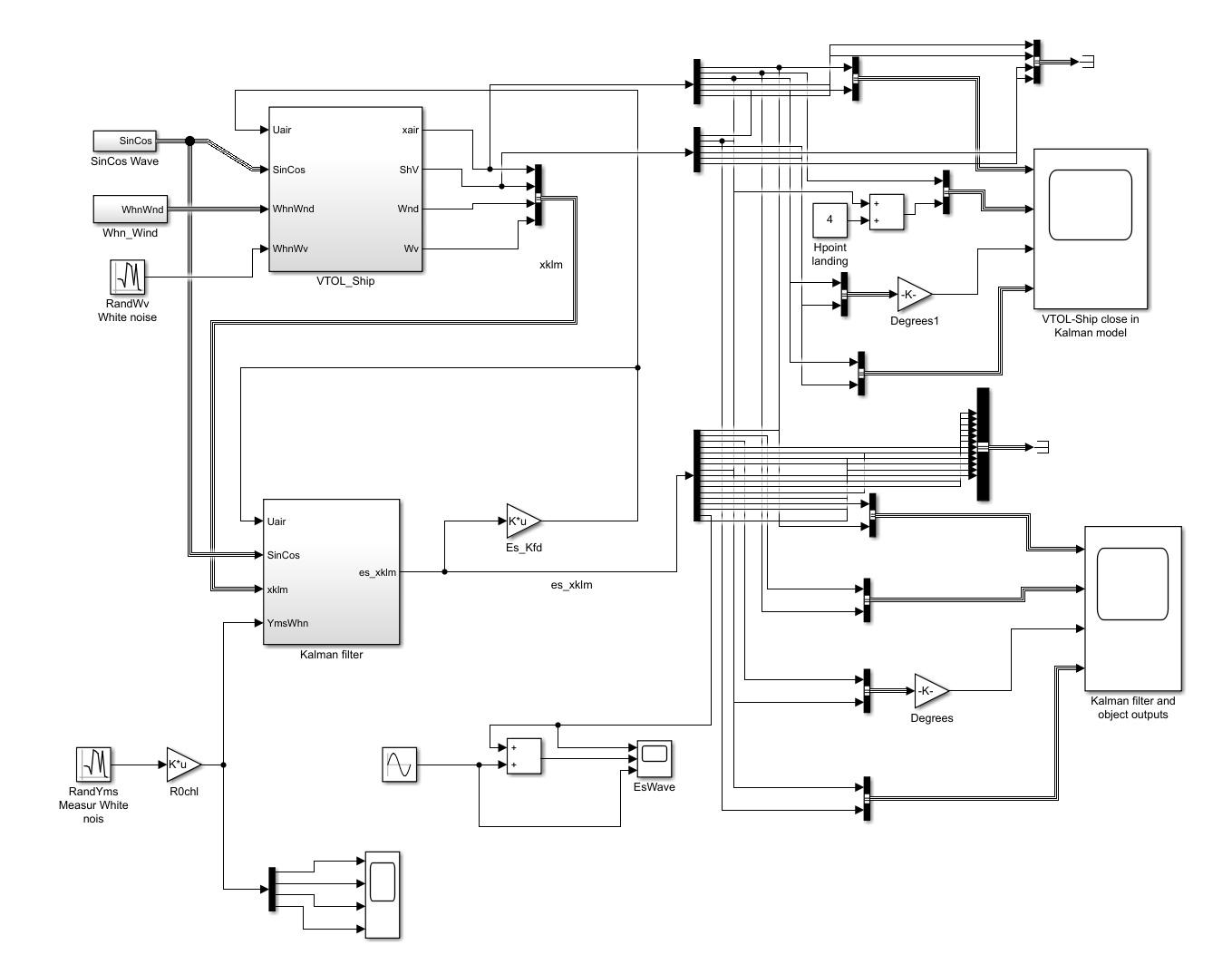 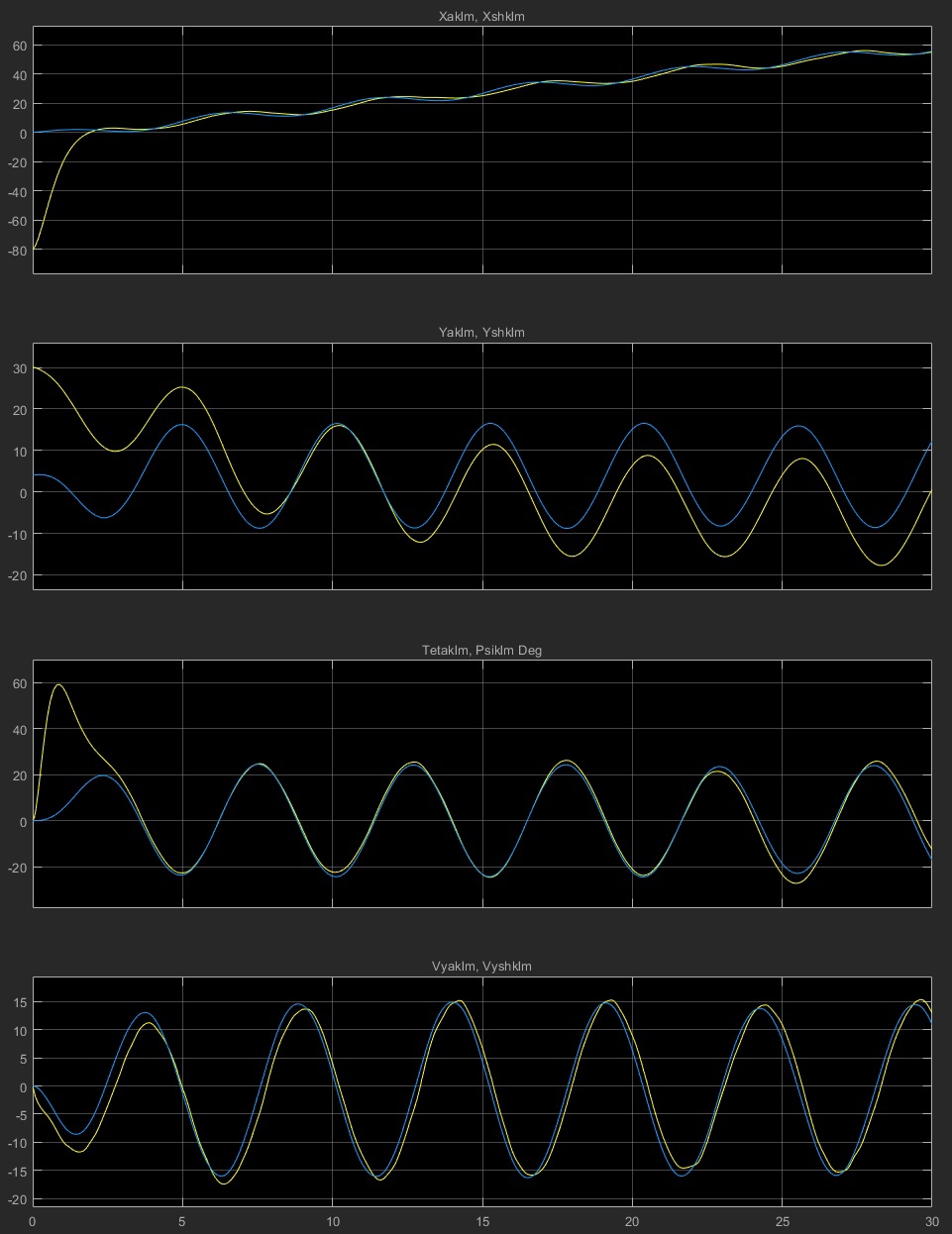 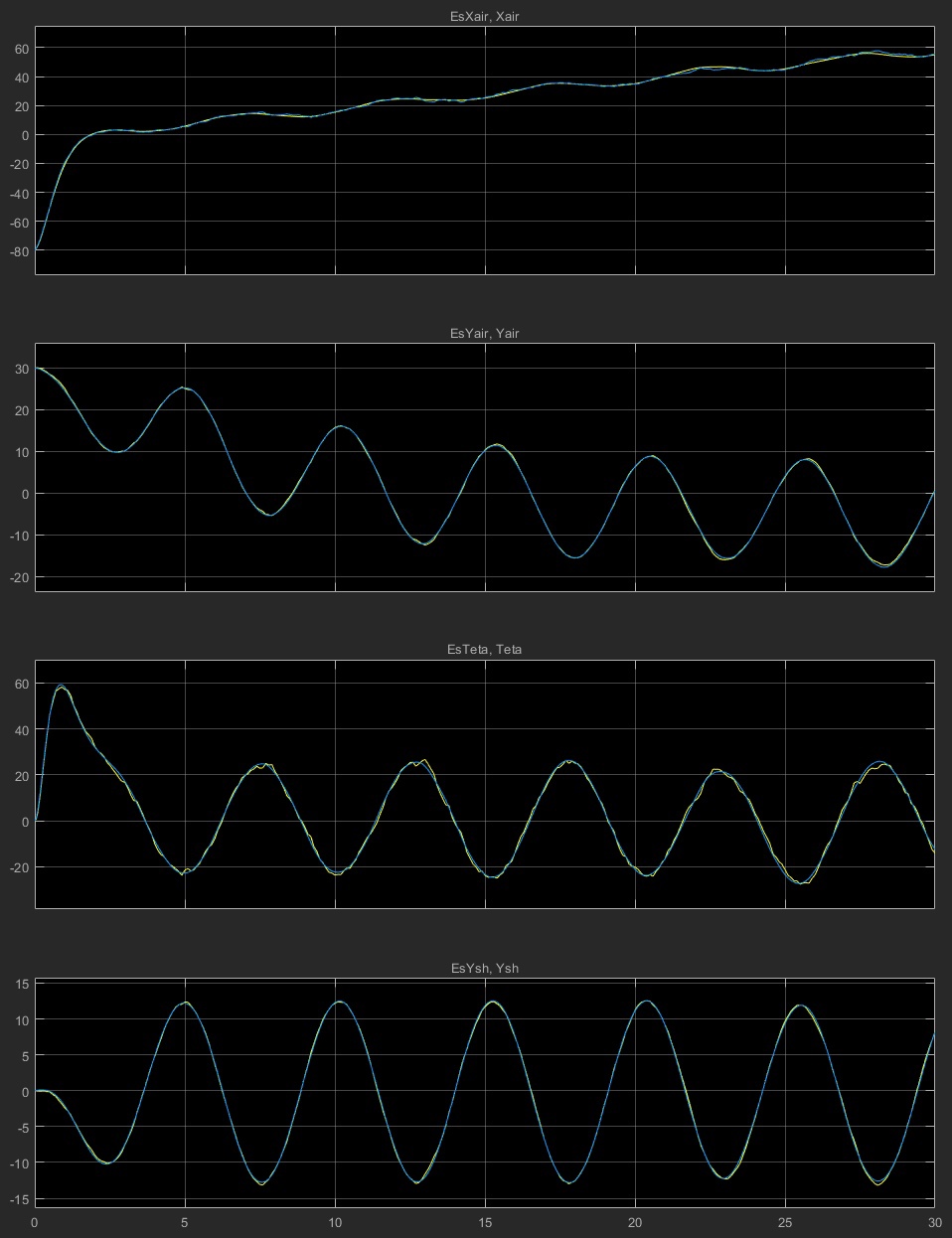 Examine Simulink close in model results. Then press any key В данной лабораторной работе рассмотрена посадка БПЛА с учетом 3 различных погодных условий: Отсутствие волнения моря и ветра. В первом случае мы видим, что БПЛА пролетел расстояние равное 34.5075,в то время как корабль прошел расстояние равное 34.5163. Скорость БПЛА и корабля по оси Х равна 2, в то время как скорость БПЛА по оси Y равна -0.4339 а корабля 0, что свидетельствует о посадке. БПЛА приземлится за время равное 17.2581. Наличие регулярного волнения моря, при отсутствии ветра. Во втором случае, мы наблюдаем на графике как БПЛА догоняет корабль, а потом начинает колебаться вместе с его кармой. БПЛА приземлится через время равное 8.9308. Наличие случайного волнения моря и случайного ветра. В третьем случае, БПЛА быстро догоняет корабль, затем зависает над кормой и начинает колебаться вместе с ней (характер похож на второй случай). В этом случае самолет приземлиться за время равное 8.8183. Вертикальные скорости БПЛА и судна также отличаются друг от друга, но после посадки, они начинают одинаково колебаться. Теперь воспользуемся фильтром Калмана. Промоделировав систему с использованием фильтра Калмана, видим, что оценка местоположения беспилотником в вертикальной и горизонтальной плоскостях совпадает с его истинным местоположением в этих же плоскостях, оценка по углу тангажа БПЛА и истинного значения – совпадают и оценка расположение кормы – совпадают. |
