Форма отчёта ЛР5. Лабораторная работа 5 Построение и исследование схем дискретной логики, используемых при создании помехоустойчивых кодеков
 Скачать 0.54 Mb. Скачать 0.54 Mb.
|
|
Московский Технический Университет Связи и Информатики Кафедра радиотехнических систем ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ Лабораторная работа №5 Построение и исследование схем дискретной логики, используемых при создании помехоустойчивых кодеков. Выполнил: Петров И. П. Гр 1111 Преподаватель: Русанов В.Э. Москва 2011 Цель работы: изучение принципа построения и работы схем дискретной логики, используемых при создании помехоустойчивых кодеков. Исходные данные по варианту №4 Закодируем две буквы моей фамилии Евдокимова согласно таблице №1 методических указаний ЕВ= 0010100010 а=0010100010 a(x)= x7+x5+x Образующий полином из таблицы №2 g(x)=478=0001001112=x5+x2+x+1 Предварительный расчёт: Умножим исходный полином на образующий c(x)=a(x)*g(x)= (x7+x5+x)*( x5+x2+x+1)= x12+x11+ x10 +x9+x7+x6+ x5+x3+ x2+x 10100010 x 100111 --------------------------- 10100010 10100010 10100010 10100010 10100010 ---------------------------- 1111011101110=C Произведём деление с(x)/g(x) 111101011101110 |_100111 100111 | 1110 110100 100111 101111 100111 010001 000000 Полученное частное равно (10100010)= a(x). Остаток равен нулю Произведём деление [с(x)+x]/g(x) 111101011101110 |_100111 100111 | 1110 110100 100111 101111 100111 010001 000000 Полученное частное равно (10100010)= a(x). Остаток равен (11011) Ход работы: Построение регистра сдвига битовых последовательностей. 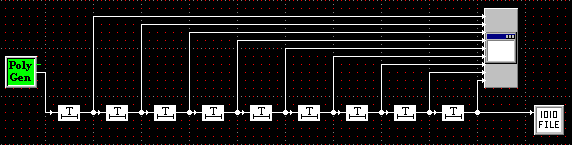 Рис.1 Регистр сдвига битовых порследовательностей Генератор полинома выдаёт исходную битовую последовательность fа затем нули 0010100010 00000000000000000, которую можно наблюдать на выходах сдвиговых регистров с помощью битовой консоли. Данные битовой консоли приведены на рис.2 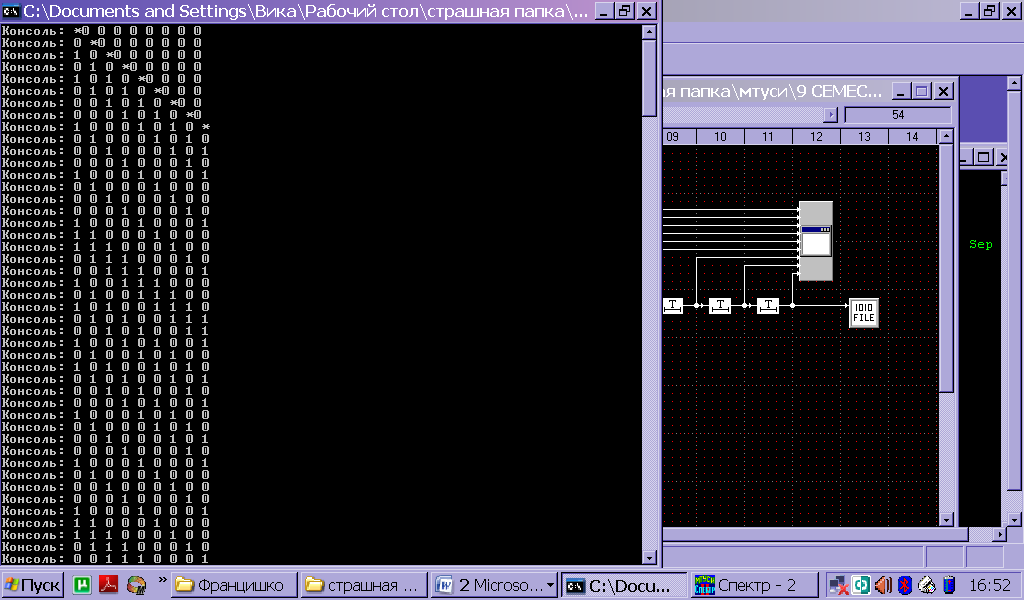 Рис.2 Данные битовой консоли для регистра сдвига Сохранённые бинарные данные представлены ниже, в них тоже видна периодически повторяющаяся входная последовательность за исключенеим того, что она выходит младшими битами вперёд, а в начале последовательности есть нулевые биты, соответствующие выходу заранее заданных нулевых состояний регистров сдвига. Построение схемы перемножения полиномов-битовых последовательностей. 2а) Перемножитель полиномов по схеме Фибоначчи примет вид, изображенный на рис.3. Отводы от регистров на элементы сложения по модулю 2 соответствуют умножению входной последовательности на полином g(x) =0001001112=x5+x2+x+1 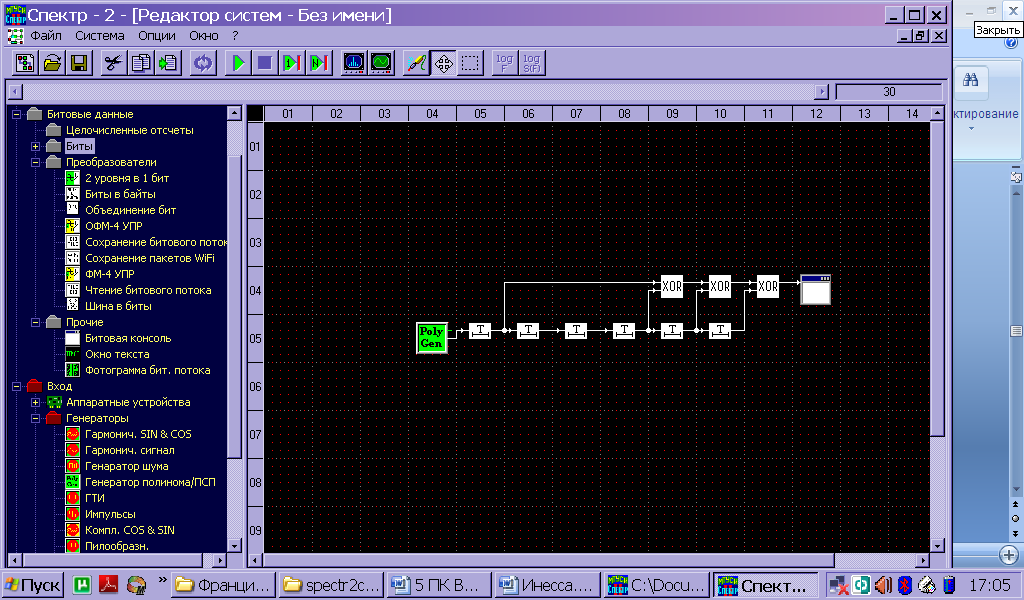 Рис.3 Перемножитель полиномов-битовых последовательностей по схеме Фибоначчи. Выходная последовательность, представленная на рис.4, соответствует предварительно рассчитанному произведению c=a*g=1111011101110 Код произведения начинается с ___ такта работы перемножителя. 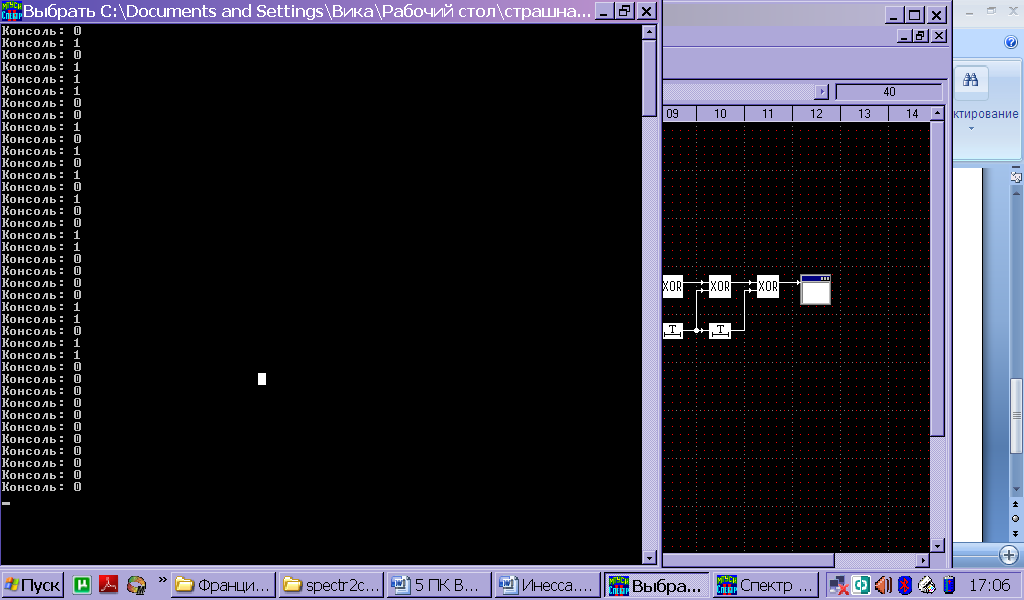 Рис.4 Данные битовой консоли при работе схемы Фибоначчи для умножения полиномов 2б) Схема Галуа для перемножения полиномов примет вид, изображенный на рис. 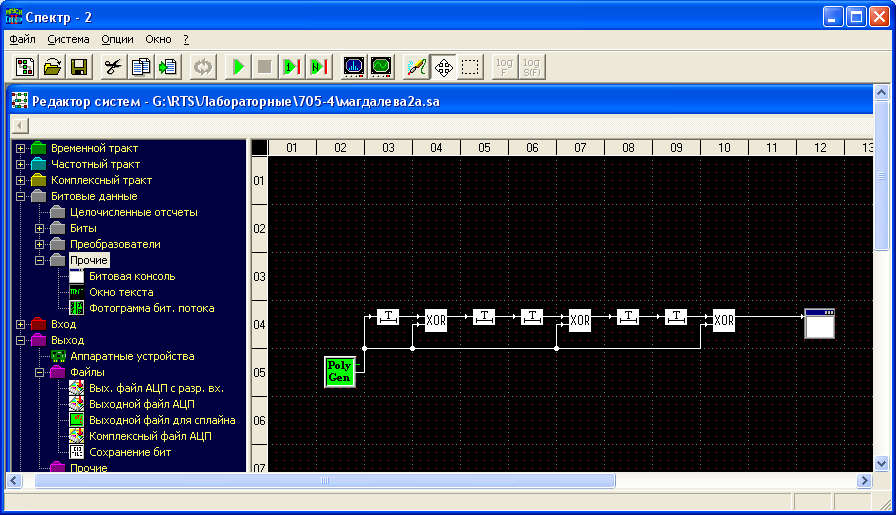 Рисунок схемы. Выходная последовательность, представленная на рис., соответствует предварительно рассчитанному произведению c=a*g=00010111001010101001100001101100 Рисунок данных консоли  Построение схем для деления полиномов. 3а) Схема Фибоначчи для деления полиномов. 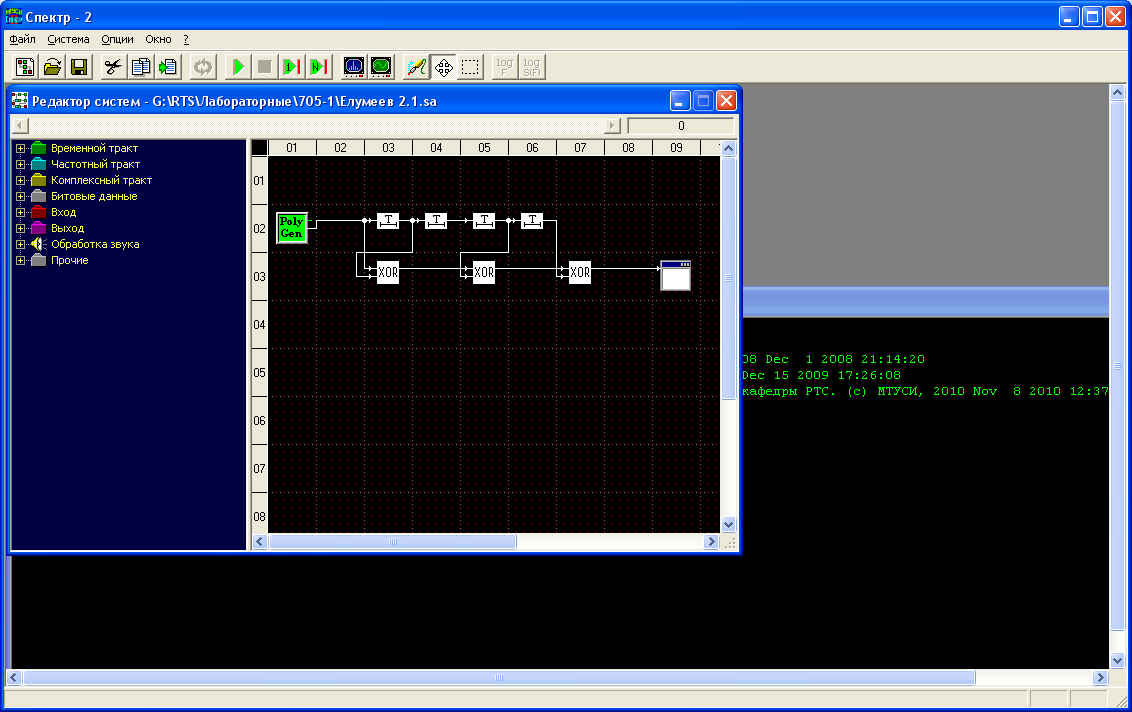 Получим схему деления полиномов, вычисляющую частное (оследовательность бит на выходе регистра) и остаток от деления c(x) на g(x) (состояние ячеек регистра делителя к моменту завершения операции деления), На шаге работы, битовая консоль выдаёт остаток вида 000000. Это означает что кратны и делятся без остатка. Как результат работы делителя на рис. представлены данные битовой консоли. (на консоль вывести выход источника, выходы ячеек регистра ) 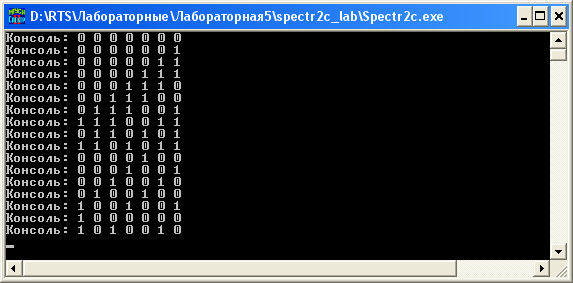 3б) Схема Галуа для деления полиномов. 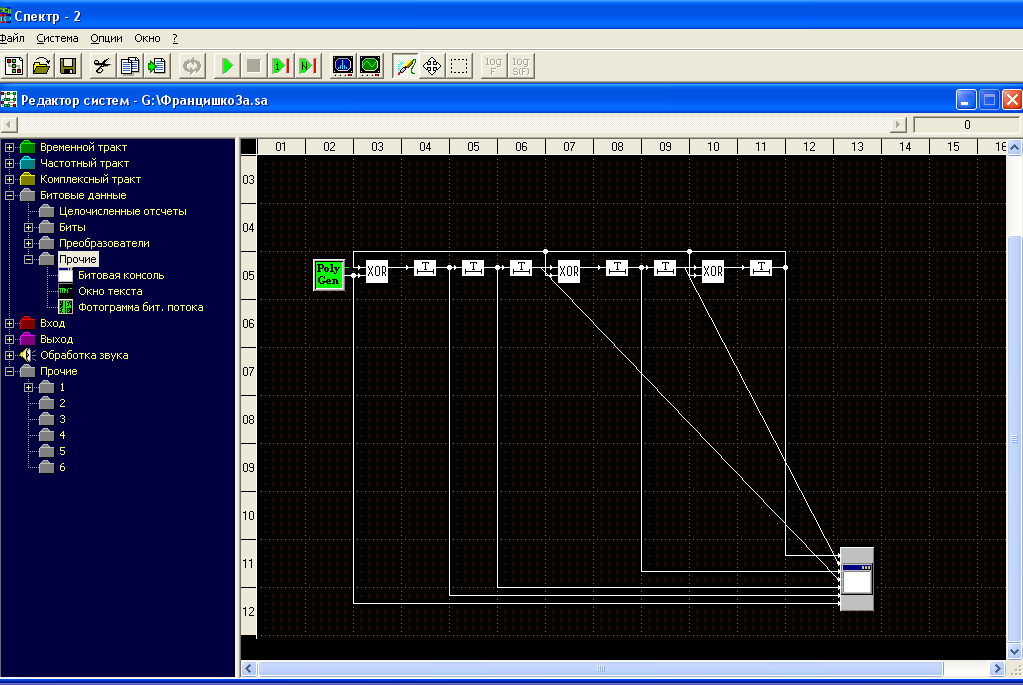 Рис.5 Схема деления полиномов, делитель – полином g(x) Получим схему деления полиномов, вычисляющую частное (оследовательность бит на выходе регистра) и остаток от деления c(x) на g(x) (состояние ячеек регистра делителя к моменту завершения операции деления), На шаге работы, битовая консоль выдаёт остаток вида 000000. Это означает что кратны и делятся без остатка. Как результат работы делителя на рис. представлены данные битовой консоли. (на консоль вывести выход источника, выходы ячеек регистра )  Рисунок Отображение результатов работы делителя на битовой консоли. Первые 6 цифр консоли в последней строке показывают остаток деления: 101001. Остаток появляется на выходах ячеек регистра на следующий такт после выхода последнего разряда частного ( оно в первом столбце 101000011) и поступления с генератора последнего разряда входного сигнала ( он в последнем столбце 111001111010010). Изменим исходные данные, заменив с(x)на C`(x)=c(x)+x, что соответствует делению с остатком. Прибавление x – это инверсия предпоследнего разряда делимого. Найдём остаток от деления с(x)+x на g(x). Он должен быть ненулевым. Индикация работы делителя представлена на рис.  Рисунок данные битовой консоли. (на консоль вывести выход источника, выходы ячеек регистра ) На шаге работы, битовая консоль выдаёт остаток. 4а) Построение схемы генератора псевдослучайной последовательности по схеме Фибоначчи. 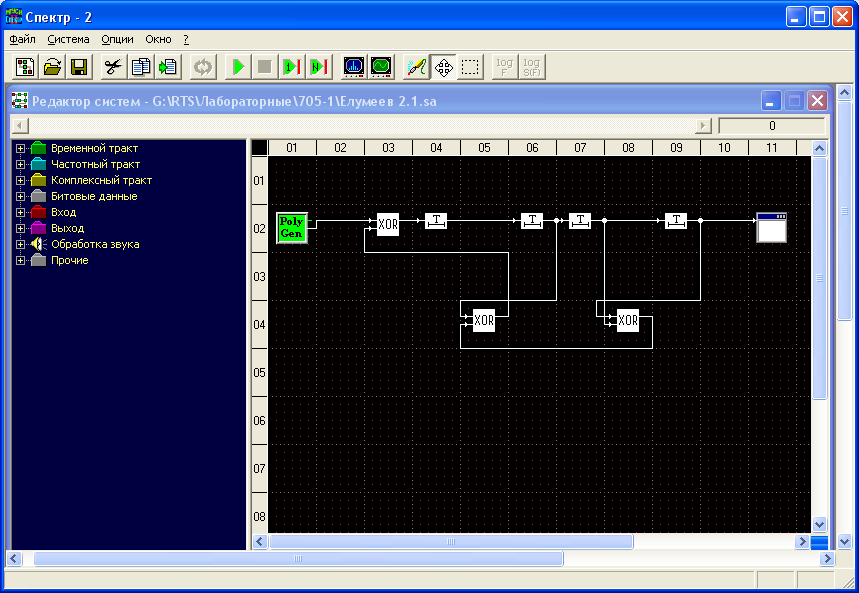 Рисунок Генератор псевдослучайной последовательности. Схема Фибоначчи.  Рисунок Фотограмма ПСП Период генерируемой ПСП равен ____. 4б) Построение схемы генератора псевдослучайной последовательности по схеме Галуа. 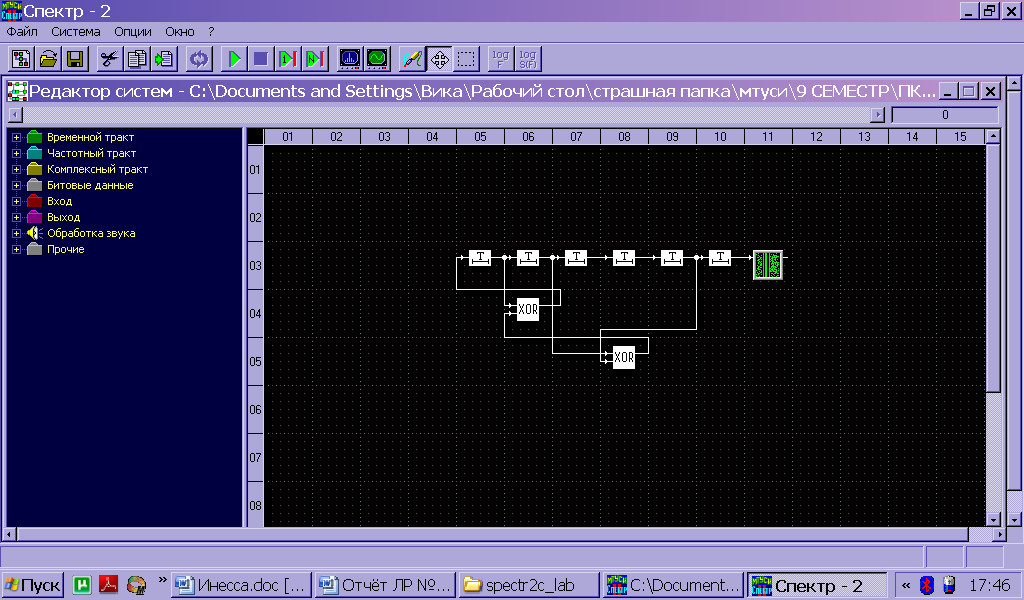 Рис.8Схема генератора ПСП Определим период генерируемой последовательности, добившись того, чтобы фотограмма (рис.9) этой ПСП представляла собой вертикальные прямые линии.  Рис.9 Фотограмма ПСП Период генерируемой ПСП равен ____. Выводы: Изучен принцип работы умножителя многочленов на элементах дискретной логики по схемам Галуа и Фибоначчи. Результаты, полученные с помощью лабораторного стенда совпали с даннвми предварительного расчёта. Изучен принцип работы делителя многочленов на элементах дискретной логики по схемам Галуа и Фибоначчи. Результаты, полученные с помощью лабораторного стенда совпали с данными предварительного расчёта На базе схем деления полиномов построены схемы генераторов псевдослучайных последовательностей. Период ПСП генерируемой по лабораторному заданию равен (не равен) максимально возможному значению 2n-1, где n –порядок образующего многочлена g(x). Причина этого в том, что g(x) …приводимый (неприводимый многочлен. |
