Давай. Лабораторная работа 6 а Определение момента инерции тел методом крутильных колебаний
 Скачать 153.5 Kb.
|
|
Лабораторная работа № 6 а Определение момента инерции тел методом крутильных колебаний Выполнил студент гр. ________________ Ф.И.О. _____________________ Подпись преподавателя _______________ Дата _____________________ Цель работы – изучить метод крутильных колебаний для расчета момента инерции тел разной формы. Сравнить экспериментальные значения моментов инерции этих тел с теоретическими расчетами. Порядок выполнения работы  Рис.22 1. Измерить линейкой радиусы верхнего и нижнего дисков R и r, а также длину нитиl. Занести данные в таблицу 1. 2. Резко повернуть рукой верхний диск Д до упора и отпустить (см. рис.22). При этом нижний диск-платформа П должен совершать крутильные колебания, а верхний диск Д должен остаться в покое из-за трения в оси. 3. С помощью секундомера определить время t1 полных n = 20 колебаний ненагруженного диска. Опыт повторить три раза. Вычислить среднее значение этого времени  и среднее значение периода колебаний  . Результаты измерений и вычислений занести в таблицу 1.
4. Положить на нижний диск первое исследуемое тело так, чтобы центры масс тела и диска были на одной оси. Величина массы нижнего диска-платформы  и массы m всех исследуемых тел указаны на установке или нанесены на этих телах. 5. Определить время  полных n = 20 колебаний нагруженного диска. Опыт повторить три раза. Вычислить среднее значение  и среднее значение периода колебаний  . Результаты измерений и вычислений занести в таблицу 2.6. Используя полученные данные, вычислить момент инерции 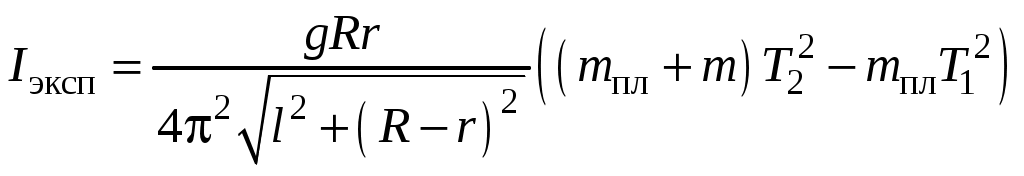 исследуемого тела по формуле  и занести полученный результат в таблицу 2.7. Измерить размеры каждого исследуемого тела. По приведенной в таблице 3 для данной формы тела формуле вычислить теоретический момент инерции  этого тела относительно той же оси, что и при эксперименте. Занести полученный результат в таблицу 2.8. Сравнить теоретическое и экспериментальное значения момента инерции. Для этого вычислить относительное отклонение этих величин по формуле  , где  .9. Повторить аналогичные измерения и вычисления с пункта 4 по пункт 8 для двух других тел, приведенных в таблице 3. Результаты занести в таблицу 2. Таблица 2.
Таблица 3. Моменты инерции плоских тел относительно оси, проходящей через центр масс перпендикулярно их плоскости.
Контрольные вопросы и задания к лабораторной работе № 6а 1. Дайте определение и объясните физический смысл момента инерции материальной точки и физического тела. 2. Сформулируйте теорему Штейнера.  Рис.А 3. Из одинаковых тонких жестяных деталей в виде ромба сделали, разрезав их на части, и раздвинув на одинаковые расстояния от оси вращения, четыре плоские фигуры (рис.А). Расставьте моменты инерции Ii этих фигур в порядке возрастания их величин и объясните свой ответ.  Рис.Б 4. Два одинаковых тонких стержня с массой m и длиной l каждый приварены концами под прямым углом друг к другу. Найти момент инерции этого угольника относительно перпендикулярной оси A, показанной на рис.Б. 5. Как вычислить момент инерции относительно оси симметрии, проходящей через центр масс плоской пластины? Проделайте этот вывод и получите расчетные формулы для моментов инерции плоской прямоугольной пластины и диска.  Рис.В 6. Получите расчетную формулу для момента инерции пластины в форме равностороннего треугольника относительно оси, лежащей в плоскости пластины и проходящей через одну из его сторон (рис.В). 7. Объясните метод крутильных колебаний, которым в данной работе экспериментально определяются моменты инерции исследуемых пластин. Как надо размещать пластины на платформе? 8. По каким причинам угол отклонения платформы от положения равновесия должен быть малым? В каком случае платформа будет совершать гармонические колебания? 9. Как максимальная угловая скорость платформы связана с амплитудой колебаний и с высотой подъёма платформы? 10. Сформулируйте закон сохранения полной механической энергии и объясните, каким образом его можно использовать в данной работе. 11. Проделайте и объясните вывод формул 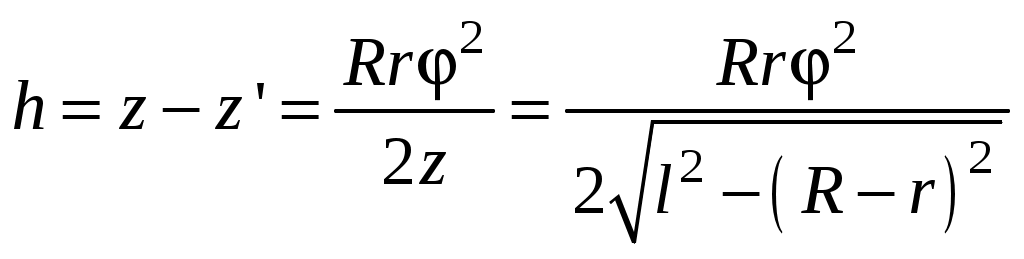 и  .12. Объясните возможные причины несоответствия величин моментов инерции, получаемых в данной работе экспериментальным способом и с помощью теоретических формул. Литература 1. Савельев И.В. Курс физики в 3-х тт.: Т. 1: Механика. Молекулярная физика - М.: Наука, 1986. - §§ 39, 41, 54. 2. Колмаков Ю.Н., Пекар Ю.А., Лагун И.М., Лежнева Л.С. Механика и теория относительности,- изд. ТулГУ. 2010, - гл.7 §1-5; гл.9 §1,2. |
, с
