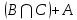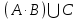Лабораторная №6 (млита) (копия). Лабораторная работа 6 Основы нечеткой логики по дисциплине Математическая логика и теория алгоритмов
 Скачать 62.94 Kb. Скачать 62.94 Kb.
|
|
Федеральное агентство связи ордена Трудового Красного Знамени Федеральное государственное бюджетное образовательное учреждение высшего образования Московский технический университет связи и информатики Кафедра «Информатика» Лабораторная работа №6 «Основы нечеткой логики» по дисциплине: «Математическая логика и теория алгоритмов» Выполнил студент группы БСТ2205 Соловьев Максим Вариант №12 Проверил проф. Семин В.Г. Москва 2023 Условие задачи 1. Нахождение основных характеристик нечеткого множестваДля заданного дискретного нечеткого множества А найти носитель, ядро, высоту, мощность, множества уровня (для заданных значений α). Указать, является ли данное множество нормальным. Если является субнормальным, преобразовать его к нормальному. Проверить является ли нормализованное множество унимодальным.
Решение задачи 1Для заданного дискретного нечеткого множества A найти носитель, ядро, высоту, мощность, множества уровня (для заданных значений α). Указать, является ли данное множество нормальным. А = {0,2/-2; 0,3/-1; 0,7/0; 1/1; 0,6/2; 0,3/3; 0,1/4}; α1=0,3; α2=0,8. Supp A = {x/µA(x) > 0} = {-2; -1; 0; 1; 2; 3; 4} - носитель, Core A = {x/ µA(x) = 1} = {1} - ядро, d = {max µA(x)}=1 - высота, т.к. верхняя граница его функции принадлежности равна 1. Card A = 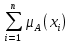 = 0.2+0,3+0,7+1+0,6+0,3+0,1=3,2 – мощность, = 0.2+0,3+0,7+1+0,6+0,3+0,1=3,2 – мощность,A0,3 = {x/ µA(x) ≥ 0,3} = {-1; 0; 1; 2; 3} – множество уровня для α1=0,3, A0,8 = {x/ µA (x) ≥ 0,8} = {1} – множество уровня для α2=0,8, d = {max µA(x)} =1, следовательно множество A нормальное или унимодальное, а так как нечеткое множество унимодальное, если µA(x) = 1 только на одном х из Е, а у нас µA(x) = 1 на одном х из Е, следовательно, заданное дискретное нечеткое множество А унимодальное. Условие задачи 2. Операции над нечеткими множествамиДано 3 нечетких множества A, B, C (заданы их функции принадлежности). Построить функцию принадлежности нечеткого множества D. Вариант 6.  Решение задачи 2Множество  , значит, последовательность операций будет следующей: , значит, последовательность операций будет следующей: 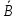 (рис. 1), (рис. 1), 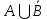 (рис. 2), (рис. 2), 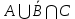 (рис. 3). (рис. 3).Построим согласно этой последовательности операций графики функций принадлежности:  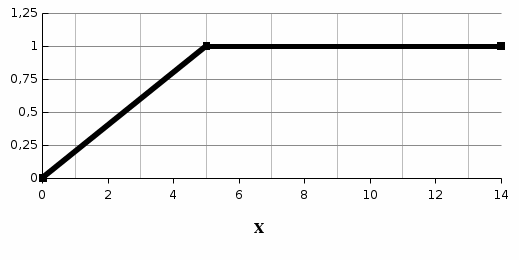 Рисунок 1 - Функция принадлежности множества 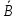 Пояснения: мы берем график B и строим новый по тем же точкам, но как бы «переворачиваем», «берем наоборот». Так, была точка (0,1), то она становится точкой (0,0), точка (5,0) станет точкой (5,1). 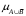  Рисунок 2 - Функция принадлежности множества 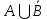 Пояснения: Объединение нечетких множеств A и 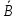 , заданных на универсальном множестве X, – это наименьшее нечеткое множество , заданных на универсальном множестве X, – это наименьшее нечеткое множество 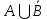 , включающеекакA, таки , включающеекакA, таки 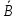 сфункциейпринадлежности. сфункциейпринадлежности.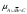 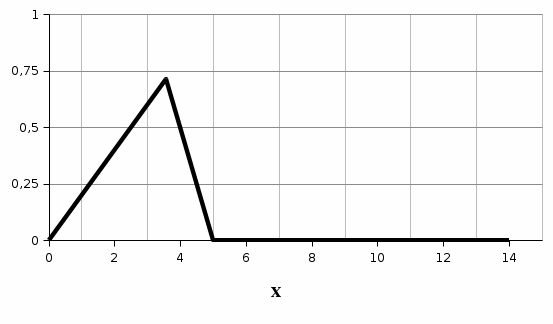 Рисунок 3 - Функция принадлежности множества 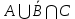 Пояснения: Пересечение нечетких множеств 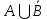 и и 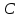 , заданных на универсальном множестве X, – это наибольшее нечеткое множество , заданных на универсальном множестве X, – это наибольшее нечеткое множество 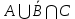 , содержащееся одновременно и в , содержащееся одновременно и в 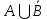 , и в , и в 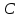 с функцией принадлежности. с функцией принадлежности.Условие задачи 3Нечеткие множества А, В и С заданы таблично. Вычислить значение выражений.
Решение задачи 3Запишем исходные данные: А= 1/х1+0,9/х2+0,7/х3+0.3/х4+0,5/х5+0,6/х6+0,7/х7+0,8/х8 В=0,3/х1+0,5/х2+ 0,4/х3+0,2/х4+0,1/х5+0,1/х6+0,5/х7+0,7/х8 С=0,1/х1+0,3/х2+ 0/х3+ 0,6/х4+0,8/х5+1/х6+0,4/х7+0,1/х8 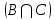 =min(μВx;μСx)=0,1/х1+0,3/х2+0/х3+0,2/х4+0,1/х5+0,1/х6+0,4/х7+0,1/х8 =min(μВx;μСx)=0,1/х1+0,3/х2+0/х3+0,2/х4+0,1/х5+0,1/х6+0,4/х7+0,1/х8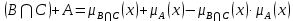 =0,1/х1+1/х1-0,1/х1 =0,1/х1+1/х1-0,1/х1 1/х1+0,3/х2+0,9/х2-0,3/x2 1/х1+0,3/х2+0,9/х2-0,3/x2 0,9/х2+0/х3+0,7/х3-0/х3 0,9/х2+0/х3+0,7/х3-0/х3 0,7/х3+0.2/х4+0,3/х4-0,2/х4 0,7/х3+0.2/х4+0,3/х4-0,2/х4 0.3/х4+0,1/х5+0,5/х5-0,1/х5 0.3/х4+0,1/х5+0,5/х5-0,1/х5 0,5/х5+0,1/х6+0,6/х6-0,1/х6 0,5/х5+0,1/х6+0,6/х6-0,1/х6 0,6/х6+0,4/х7+0,7/х7-0,4/х7 0,6/х6+0,4/х7+0,7/х7-0,4/х7 0,7/х7+0,1/х8+0,8/х8-0,1/х8 0,7/х7+0,1/х8+0,8/х8-0,1/х8 0,8/х8=1/x1+0,93/x2+0,7/x3+0.44/x4+0,55/x5+0,64/x6+0,82/x7+0,82/x8 0,8/х8=1/x1+0,93/x2+0,7/x3+0.44/x4+0,55/x5+0,64/x6+0,82/x7+0,82/x8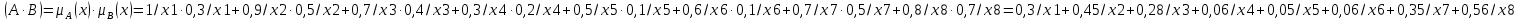 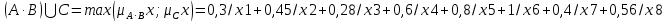 Запишем данные в таблицу
РезультатыЗадание 1: Supp A = {-2; -1; 0; 1; 2; 3; 4}; Core A = {1};Sup А = 1; Card A = 3,2; A0,3 ={-1; 0; 1; 2; 3}; A0,8 ={1}; субнормальное. Задание 2:   Задание 3:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||