Лабораторная работа №6 КГ. Лабораторная работа №6 Растровые алгоритмы_Кривая Безье. Лабораторная работа 6. Тема Базовые растровые алгоритмы. Построение кривых Безье. Закраска области

• Название: Лабораторная работа 6. Тема Базовые растровые алгоритмы. Построение кривых Безье. Закраска области
• Анкор: Лабораторная работа №6 КГ
• Дата: 02.04.2021
• Размер: 246 Kb.
• Имя файла: Лабораторная работа №6 Растровые алгоритмы_Кривая Безье.doc
• Тип: Лабораторная работа; #190511

Лабораторная работа №6.

Тема: Базовые растровые алгоритмы. Построение кривых Безье. Закраска области
1. Растровые алгоритмы

Большинство графических устройств являются растровыми, представляя изображение в виде прямоугольной матрицы (сетки, целочисленной решетки) пикселей (растра), и большинство графических библиотек содержат внутри себя достаточное количество простейших растровых алгоритмов.
Задача : создание приложения, реализующего основные алгоритмы растеризации линии и окружности

Использованный API : .NET Framework 3.5

Язык : Visual C#

Среда разработки : MS Visual Studio 2008

Описание

П 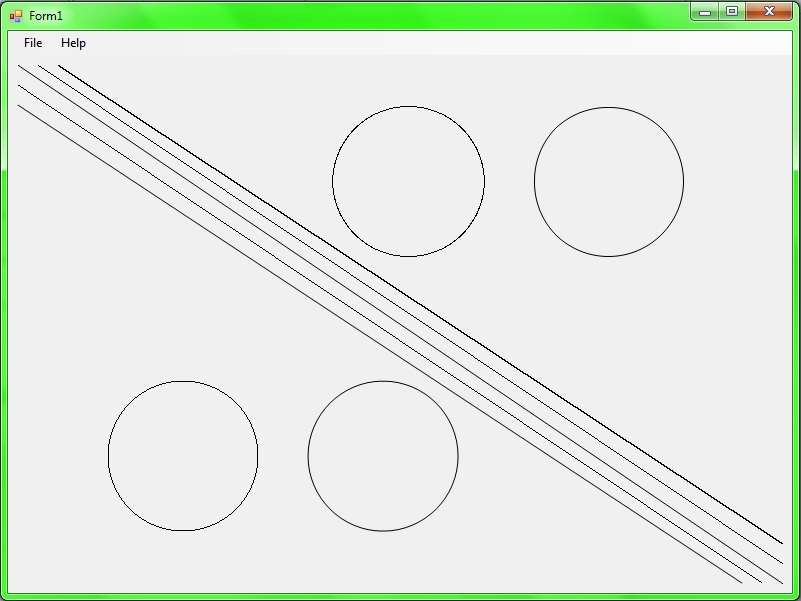редставленное приложение (Рис.4.1) реализует некоторые растровые алгоритмы. Среди них алгоритмы Брезенхема и Ву. Также для сравнения представлены аналогичные графические примитивы, встроенные в платформу .NET. В программе ведется работа с двумя классами : класс Form1, наследующий класс Form и выводящий изображения на форму, и статический класс RasterAlgorithms, содержащий реализации алгоритмов в статических методах. Далее описаны реализованные алгоритмы.

Рис.4.1 Окно приложения для реализации растровых алгоритмов

1. 
   Алгоритм Брезенхема для 4-связной линии
   

public static void Bresenham4Line(Graphics g, Color clr, int x0, int y0, int x1, int y1)
Алгоритм основан на том, что для каждой точки растра существует ровно 4 соседних точки. Это означает, что две соседние точки могут отличаться друг от друга только по одной координате и только на 1 единицу. Т. е. для точки (x, y) соседними являются точки (x+1, y), (x-1, y), (x, y+1), (x, y-1). Точка (x+1, y+1) может оказаться закрашенной только если закрашена точка (x+1, y) или (x, y+1). Алгоритм Брезенхема модифицированный по такому закону реализован в данной программе.


1.2 Алгоритм Брезенхема для 8-связной линии


static public void Bresenham8Line(Graphics g, Color clr, int x0, int y0, int x1, int y1)

Данный алгоритм предполагает, что у каждой точки растра существует ровно 8 соседних точек. Т. е. приращение абсциссы и ординаты может одновременно составлять +/- 1.

Таким образом у точки (x, y) появляется 4 новых соседки : (x+1, y+1), (x-1, y+1), (x-1, y-1), (x+1, y-1).

1.3 Алгоритм Ву Сяолиня растеризации линии с антиалиасингом


public static void DrawWuLine(Graphics g, Color clr, int x0, int y0, int x1, int y1)
Алгоритм использует механизмы сглаживания при растеризации линии. При этом ступенчатые выступы на линии становятся менее заметны. Этот эффект достигается следующим образом. На первом шаге для точки, лежащей на линии, вычисляются две ближайшие точки растра. Далее между этими двумя точками распределяется прозрачность(альфа-канал) цвета пиксела пропорционально близости пиксела к линии таким образом, чтобы суммарная яркость была равна единице. При таком распределении человеческий глаз воспринимает последовательность нескольких пикселов с взаимодополняющими значениями прозрачности как непрерывную линию, причем достаточно гладкую. В программе реализован упрощенный алгоритм, в котором некоторые вычисления производятся в вещественном формате, а также учитываются особенности платформы разработки, что замедляет работу алгоритма.


1.4 Алгоритм Брезенхема для окружности


public static void BresenhamCircle(Graphics g, Color clr, int _x, int _y, int radius)
Это реализация алгоритма Брезенхема для окружности. Вычисляется ближайший к окружности пиксел с учетом правила Брезенхема. Этот алгоритм дает возможность достаточно быстро растеризовать окружность в виде 8-связной линии.


1.5 Алгоритм Ву Сяолиня для растеризации окружности

с антиалисингом (сглаживанием)


public static void DrawWuCircle(Graphics g, Color clr, int _x, int _y, int radius)
Представляет собой измененный алгоритм растеризации линии. Для точки окружности выбираются два ближайших пиксела. между ними пропорционально распределяется прозрачность цвета. При оптимизации данного алгоритма можно учитывать, что более яркие пикселы, лежащие на внутренней части линии, придают вогнутость линии, а лежащие на внешней стороне - выпуклость.
Листинг приложения для реализации растровых алгоритмов

//file Form1.cs

 

using System;

using System.Drawing;

using System.Windows.Forms;

 

namespace RasterAlgorithms

{

public partial class Form1 : Form

{

//Метод Main() - точка входа в программу

public static void Main()

{

using (Form1 frm = new Form1())

{

 

Application.Run(frm);

}

}

 

//Конструктор пользовательского класса, наследующего класс Form

public Form1()

{

InitializeComponent();

ResizeRedraw = true;

}

 

//Обработчик события OnPaint. Отрисовывает на форме её содержимое

protected override void OnPaint(PaintEventArgs e)

{

//Устранение ошибки смещения на 1 пиксел

e.Graphics.PixelOffsetMode = System.Drawing.Drawing2D.PixelOffsetMode.HighQuality;

 

//Отрисовка 4-связной линии, построенной по алгоритму Брезенхема

RasterAlgorithms.Bresenham4Line(

e.Graphics,

Color.Black,

50, 34, ClientSize.Width - 10, ClientSize.Height - 50);

 

//Отрисовка 8-связной линии, построенной по алгоритму Брезенхема

RasterAlgorithms.Bresenham8Line(

e.Graphics,

Color.Black,

30, 34, ClientSize.Width - 10, ClientSize.Height - 30);

 

//Отрисовка линии, построенной по алгоритму Ву

RasterAlgorithms.DrawWuLine(

e.Graphics,

Color.Black,

10, 34, ClientSize.Width - 10, ClientSize.Height - 10);

 

//Обычная линия

e.Graphics.DrawLine(new Pen(Color.Black),

10, 54, ClientSize.Width - 30, ClientSize.Height - 10);

 

//Настройки сглаживания

e.Graphics.SmoothingMode = System.Drawing.Drawing2D.SmoothingMode.AntiAlias;

//Линия с установленными параметрами сглаживания

e.Graphics.DrawLine(new Pen(Color.Black),

10, 74, ClientSize.Width - 50, ClientSize.Height - 10);

 

//Отрисовка окружности, построенной по алгоритму Брезенхема

RasterAlgorithms.BresenhamCircle(

e.Graphics,

Color.Black,

400, 150, 75);

 

//Отрисовка окружности, построенной по модифицированному алгоритму Ву

RasterAlgorithms.DrawWuCircle(

e.Graphics,

Color.Black,

600, 150, 75);

 

//Окружность

e.Graphics.SmoothingMode = System.Drawing.Drawing2D.SmoothingMode.None;

e.Graphics.DrawEllipse(new Pen(Color.Black), 100, 350, 150, 150);

 

//Окружность с установленными параметрами сглаживания

e.Graphics.SmoothingMode = System.Drawing.Drawing2D.SmoothingMode.AntiAlias;

e.Graphics.DrawEllipse(new Pen(Color.Black), 300, 350, 150, 150);

}

//Описание элементов меню

private void toolStripMenuItem2_Click(object sender, EventArgs e)

{

Application.Exit();

}

 

private void toolStripMenuItem4_Click(object sender, EventArgs e)

{

MessageBox.Show(

"Линии (сверху вниз) : \n" +

"1. 4-связная линия, построенная по алгоритму Брезенхема\n" +

"2. 8-связная линия, построенная по алгоритму Брезенхема\n" +

"3. Линия, построенная по алгоритму Ву\n" +

"4. Линия, встроенная в платформу\n" +

"5. Линия с эффектом сглаживания, встроенная в платформу\n\n" +

"Окружности (слева направо сверху вниз) : \n" +

"1. Окружность, построенная по алгоритму Брезенхема\n" +

"2. Окружность, построенная по алгоритму Ву\n" +

"3. Окружность, встроенная в платформу\n" +

"4. Окружность с эффектом сглаживания, встроенная в платформу\n",

"Help");

}

}

 

//Статический класс, содержащий реализацию растровых алгоритмов

static class RasterAlgorithms

{

//Статический метод, реализующий отрисовку линии по алгоритму Ву

public static void DrawWuLine(Graphics g, Color clr, int x0, int y0, int x1, int y1)

{

//Вычисление изменения координат

int dx = (x1 > x0) ? (x1 - x0) : (x0 - x1);

int dy = (y1 > y0) ? (y1 - y0) : (y0 - y1);

//Если линия параллельна одной из осей, рисуем обычную линию - заполняем все пикселы в ряд

if (dx == 0 || dy == 0)

{

g.DrawLine(new Pen(clr), x0, y0, x1, y1);

return;

}

 

//Для Х-линии (коэффициент наклона < 1)

if (dy < dx)

{

//Первая точка должна иметь меньшую координату Х

if (x1 < x0)

{

x1 += x0; x0 = x1 - x0; x1 -= x0;

y1 += y0; y0 = y1 - y0; y1 -= y0;

}

//Относительное изменение координаты Y

float grad = (float)dy / dx;

//Промежуточная переменная для Y

float intery = y0 + grad;

//Первая точка

PutPixel(g, clr, x0, y0, 255);

 

for (int x = x0 + 1; x < x1; x++)

{

//Верхняя точка

PutPixel(g, clr, x, IPart(intery), (int)(255 - FPart(intery) * 255));

//Нижняя точка

PutPixel(g, clr, x, IPart(intery) + 1, (int)(FPart(intery) * 255));

//Изменение координаты Y

intery += grad;

}

//Последняя точка

PutPixel(g, clr, x1, y1, 255);

}

//Для Y-линии (коэффициент наклона > 1)

else

{

//Первая точка должна иметь меньшую координату Y

if (y1 < y0)

{

x1 += x0; x0 = x1 - x0; x1 -= x0;

y1 += y0; y0 = y1 - y0; y1 -= y0;

}

//Относительное изменение координаты X

float grad = (float)dx / dy;

//Промежуточная переменная для X

float interx = x0 + grad;

//Первая точка

PutPixel(g, clr, x0, y0, 255);

 

for (int y = y0 + 1; y < y1; y++)

{

//Верхняя точка

PutPixel(g, clr, IPart(interx), y, 255 - (int)(FPart(interx) * 255));

//Нижняя точка

PutPixel(g, clr, IPart(interx) + 1, y, (int)(FPart(interx) * 255));

//Изменение координаты X

interx += grad;

}

//Последняя точка

PutPixel(g, clr, x1, y1, 255);

}

}

 

//Статический метод, реализующий отрисовку окружности по алгоритму Ву

public static void DrawWuCircle(Graphics g, Color clr, int _x, int _y, int radius)

{

//Установка пикселов, лежащих на осях системы координат с началом в центре

PutPixel(g, clr, _x + radius, _y, 255);

PutPixel(g, clr, _x, _y + radius, 255);

PutPixel(g, clr, _x - radius + 1, _y, 255);

PutPixel(g, clr, _x, _y - radius + 1, 255);

 

float iy = 0;

for (int x = 0; x <= radius * Math.Cos(Math.PI / 4); x++)

{

//Вычисление точного значения координаты Y

iy = (float)Math.Sqrt(radius * radius - x * x);

 

//IV квадрант, Y

PutPixel(g, clr, _x - x, _y + IPart(iy), 255 - (int)(FPart(iy) * 255));

PutPixel(g, clr, _x - x, _y + IPart(iy) + 1, (int)(FPart(iy) * 255));

//I квадрант, Y

PutPixel(g, clr, _x + x, _y + IPart(iy), 255 - (int)(FPart(iy) * 255));

PutPixel(g, clr, _x + x, _y + IPart(iy) + 1, (int)(FPart(iy) * 255));

//I квадрант, X

PutPixel(g, clr, _x + IPart(iy), _y + x, 255 - (int)(FPart(iy) * 255));

PutPixel(g, clr, _x + IPart(iy) + 1, _y + x, (int)(FPart(iy) * 255));

//II квадрант, X

PutPixel(g, clr, _x + IPart(iy), _y - x, 255 - (int)(FPart(iy) * 255));

PutPixel(g, clr, _x + IPart(iy) + 1, _y - x, (int)(FPart(iy) * 255));

 

//С помощью инкремента устраняется ошибка смещения на 1 пиксел

x++;

//II квадрант, Y

PutPixel(g, clr, _x + x, _y - IPart(iy), (int)(FPart(iy) * 255));

PutPixel(g, clr, _x + x, _y - IPart(iy) + 1, 255 - (int)(FPart(iy) * 255));

//III квадрант, Y

PutPixel(g, clr, _x - x, _y - IPart(iy), (int)(FPart(iy) * 255));

PutPixel(g, clr, _x - x, _y - IPart(iy) + 1, 255 - (int)(FPart(iy) * 255));

//III квадрант, X

PutPixel(g, clr, _x - IPart(iy), _y - x, (int)(FPart(iy) * 255));

PutPixel(g, clr, _x - IPart(iy) + 1, _y - x, 255 - (int)(FPart(iy) * 255));

//IV квадрант, X

PutPixel(g, clr, _x - IPart(iy), _y + x, (int)(FPart(iy) * 255));

PutPixel(g, clr, _x - IPart(iy) + 1, _y + x, 255 - (int)(FPart(iy) * 255));

//Возврат значения

x--;

}

}

 

//Статический метод, реализующий отрисовку 8-связной линии по алгоритму Брезенхема

static public void Bresenham8Line(Graphics g, Color clr, int x0, int y0, int x1, int y1)

{

//Изменения координат

int dx = (x1 > x0) ? (x1 - x0) : (x0 - x1);

int dy = (y1 > y0) ? (y1 - y0) : (y0 - y1);

//Направление приращения

int sx = (x1 >= x0) ? (1) : (-1);

int sy = (y1 >= y0) ? (1) : (-1);

 

if (dy < dx)

{

int d = (dy << 1) - dx;

int d1 = dy << 1;

int d2 = (dy - dx) << 1;

PutPixel(g, clr, x0, y0, 255);

int x = x0 + sx;

int y = y0;

for (int i = 1; i <= dx; i++)

{

if (d > 0)

{

d += d2;

y += sy;

}

else

d += d1;

PutPixel(g, clr, x, y, 255);

x++;

}

}

else

{

int d = (dx << 1) - dy;

int d1 = dx << 1;

int d2 = (dx - dy) << 1;

PutPixel(g, clr, x0, y0, 255);

int x = x0;

int y = y0 + sy;

for (int i = 1; i <= dy; i++)

{

if (d > 0)

{

d += d2;

x += sx;

}

else

d += d1;

PutPixel(g, clr, x, y, 255);

y++;

}

}

}

//Статический метод, реализующий отрисовку 4-связной линии по алгоритму Брезенхема

public static void Bresenham4Line(Graphics g, Color clr, int x0, int y0, int x1, int y1)

{

int dx = x1 - x0;

int dy = y1 - y0;

int d = 0;

int d1 = dy << 1;

int d2 = -(dx << 1);

PutPixel(g, clr, x0, y0, 255);

int x = x0;

int y = y0;

 

for (int i = 1; i <= dx + dy; i++)

{

if (d > 0)

{

d += d2;

y++;

}

else

{

d += d1;

x++;

}

PutPixel(g, clr, x, y, 255);

}

}

//Статический метод, реализующий отрисовку окружности по алгоритму Брезенхема

public static void BresenhamCircle(Graphics g, Color clr, int _x, int _y, int radius)

{

int x = 0, y = radius, gap = 0, delta = (2 - 2 * radius);

while (y >= 0)

{

PutPixel(g, clr, _x + x, _y + y, 255);

PutPixel(g, clr, _x + x, _y - y, 255);

PutPixel(g, clr, _x - x, _y - y, 255);

PutPixel(g, clr, _x - x, _y + y, 255);

gap = 2 * (delta + y) - 1;

if (delta < 0 && gap <= 0)

{

x++;

delta += 2 * x + 1;

continue;

}

if (delta > 0 && gap > 0)

{

y--;

delta -= 2 * y + 1;

continue;

}

x++;

delta += 2 * (x - y);

y--;

}

}

//Метод, устанавливающий пиксел на форме с заданными цветом и прозрачностью

private static void PutPixel(Graphics g, Color col, int x, int y, int alpha)

{

g.FillRectangle(new SolidBrush(Color.FromArgb(alpha, col)), x, y, 1, 1);

}

//Целая часть числа

private static int IPart(float x)

{

return (int)x;

}

//дробная часть числа

private static float FPart(float x)

{

while (x >= 0)

x--;

x++;

return x;

}

}

}

 

 

//file Form1.Designer.cs

 

namespace RasterAlgorithms

{

partial class Form1

{

///

/// Required designer variable.

///

private System.ComponentModel.IContainer components = null;

 

///

/// Clean up any resources being used.

///

///
true if managed resources should be disposed; otherwise, false.


protected override void Dispose(bool disposing)

{

if (disposing && (components != null))

{

components.Dispose();

}

base.Dispose(disposing);

}

 

#region Windows Form Designer generated code

 

///

/// Required method for Designer support - do not modify

/// the contents of this method with the code editor.

///

private void InitializeComponent()

{

this.menuStrip1 = new System.Windows.Forms.MenuStrip();

this.toolStripMenuItem1 = new System.Windows.Forms.ToolStripMenuItem();

this.toolStripMenuItem2 = new System.Windows.Forms.ToolStripMenuItem();

this.toolStripMenuItem3 = new System.Windows.Forms.ToolStripMenuItem();

this.toolStripMenuItem4 = new System.Windows.Forms.ToolStripMenuItem();

this.menuStrip1.SuspendLayout();

this.SuspendLayout();

//

// menuStrip1

//

this.menuStrip1.Items.AddRange(new System.Windows.Forms.ToolStripItem[] {

this.toolStripMenuItem1,

this.toolStripMenuItem3});

this.menuStrip1.Location = new System.Drawing.Point(0, 0);

this.menuStrip1.Name = "menuStrip1";

this.menuStrip1.Size = new System.Drawing.Size(784, 24);

this.menuStrip1.TabIndex = 1;

this.menuStrip1.Text = "menuStrip1";

//

// toolStripMenuItem1

//

this.toolStripMenuItem1.DropDownItems.AddRange(new System.Windows.Forms.ToolStripItem[] {

this.toolStripMenuItem2});

this.toolStripMenuItem1.Name = "toolStripMenuItem1";

this.toolStripMenuItem1.Size = new System.Drawing.Size(37, 20);

this.toolStripMenuItem1.Text = "File";

//

// toolStripMenuItem2

//

this.toolStripMenuItem2.Name = "toolStripMenuItem2";

this.toolStripMenuItem2.Size = new System.Drawing.Size(152, 22);

this.toolStripMenuItem2.Text = "Exit";

this.toolStripMenuItem2.Click += new System.EventHandler(this.toolStripMenuItem2_Click);

//

// toolStripMenuItem3

//

this.toolStripMenuItem3.DropDownItems.AddRange(new System.Windows.Forms.ToolStripItem[] {

this.toolStripMenuItem4});

this.toolStripMenuItem3.Name = "toolStripMenuItem3";

this.toolStripMenuItem3.Size = new System.Drawing.Size(44, 20);

this.toolStripMenuItem3.Text = "Help";

//

// toolStripMenuItem4

//

this.toolStripMenuItem4.Name = "toolStripMenuItem4";

this.toolStripMenuItem4.Size = new System.Drawing.Size(152, 22);

this.toolStripMenuItem4.Text = "Help";

this.toolStripMenuItem4.Click += new System.EventHandler(this.toolStripMenuItem4_Click);

//

// Form1

//

this.AutoScaleDimensions = new System.Drawing.SizeF(6F, 13F);

this.AutoScaleMode = System.Windows.Forms.AutoScaleMode.Font;

this.ClientSize = new System.Drawing.Size(784, 562);

this.Controls.Add(this.menuStrip1);

this.MainMenuStrip = this.menuStrip1;

this.Name = "Form1";

this.Text = "Form1";

this.menuStrip1.ResumeLayout(false);

this.menuStrip1.PerformLayout();

this.ResumeLayout(false);

this.PerformLayout();

 

}

 

#endregion

 

private System.Windows.Forms.MenuStrip menuStrip1;

private System.Windows.Forms.ToolStripMenuItem toolStripMenuItem1;

private System.Windows.Forms.ToolStripMenuItem toolStripMenuItem2;

private System.Windows.Forms.ToolStripMenuItem toolStripMenuItem3;

private System.Windows.Forms.ToolStripMenuItem toolStripMenuItem4;

}

}
2. Построение кривой Безье
•Кривая Безье - это параметрическая кривая n-го порядка, которая задается следующей формулой:

x(t) = C_n⁰t⁰(1-t)ⁿx₀+ C_n¹t¹(1-t)^n-1x₁+ C_n²t²(1-t)^n-2x₂+ ... + C_nⁿtⁿ(1-t)⁰x_n
В этой формуле x_i - абсцисса i-ой точки, параметр t лежит в интервале от 0 до 1. Подобным образом задаются другие координаты.

Е 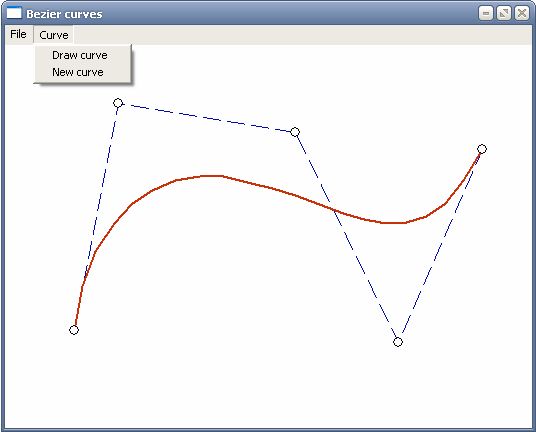сли задана последовательность, состоящая из (n-1) точек, то такая последовательность точек, называемая ломаной Безье, однозначно определяет форму кривой Безье. Изменяя положения вершин ломаной, можно управлять формой соот­ветствующей кривой Безье.

Для построения кривой Безье необходимо задать в клиентской области окна множество точек, используя мышь.

Затем, после выбора пункта меню "Draw curve" можно изменять форму кривой с помощью мыши. Пункт меню "New curve" предназначен для удаления текущей кривой и выбора точек для построения новой (рис.4.2).

Рис.4.2 Внешний вид окна приложения

Листинг программы для построения кривой Безье

#include "stdafx.h" // Заголовочный файл проекта, в который включен файл "windows.h" (#include ).

#include "Bezier curves.h"

#include

 

using namespace std; // Директива, позволяющая обращаться к

// средствам пространства имен стандартной библиотеки

// без квалификаторов доступа.

 

#define MAX_LOADSTRING 100

 

HINSTANCE hInst; // Дескриптор экземпляра приложения.

TCHAR szTitle[MAX_LOADSTRING]; // Строка, хранящая текст заголовка окна.

TCHAR szWindowClass[MAX_LOADSTRING]; // Имя класса окна.

 

ATOM MyRegisterClass(HINSTANCE hInstance);

BOOL InitInstance(HINSTANCE, int);

LRESULT CALLBACK WndProc(HWND, UINT, WPARAM, LPARAM);

 

// Функция, вычисляющая значение х и у координат точки на кривой.

POINT CalcBezierCurve(vector
, const double&);

// Процедура отрисовки кривой Безье.

void DrawBezier(HDC, vector
);

// Функция, возвращающая номер точки массива,

// по которой пользователь щелкает мышью.

int GetNumberOfPoint (int, int, vector
);

 

// Главная функция программы, в которой запускается цикл обработки сообщений.

int APIENTRY _tWinMain(HINSTANCE hInstance,

HINSTANCE hPrevInstance,

LPTSTR lpCmdLine,

int nCmdShow)

{

UNREFERENCED_PARAMETER(hPrevInstance);

UNREFERENCED_PARAMETER(lpCmdLine);

 

MSG msg;

 

LoadString(hInstance, IDS_APP_TITLE, szTitle, MAX_LOADSTRING);

LoadString(hInstance, IDC_BEZIERCURVES, szWindowClass, MAX_LOADSTRING);

MyRegisterClass(hInstance);

 

if (!InitInstance (hInstance, nCmdShow)) {

return FALSE;

}

 

while (GetMessage(&msg, NULL, 0, 0)) {

TranslateMessage(&msg);

DispatchMessage(&msg);

}

 

return (int) msg.wParam;

}

 

// Регистрация класса окна.

ATOM MyRegisterClass(HINSTANCE hInstance)

{

WNDCLASSEX wcex;

 

wcex.cbSize = sizeof(WNDCLASSEX);

  wcex.style = CS_HREDRAW | CS_VREDRAW;

wcex.lpfnWndProc = WndProc;

wcex.cbClsExtra = 0;

wcex.cbWndExtra = 0;

wcex.hInstance = hInstance;

wcex.hIcon = LoadIcon(hInstance, MAKEINTRESOURCE(IDI_BEZIERCURVES));

wcex.hCursor = LoadCursor(NULL, IDC_ARROW);

wcex.hbrBackground = (HBRUSH)(COLOR_WINDOW+1);

wcex.lpszMenuName = MAKEINTRESOURCE(IDC_BEZIERCURVES);

wcex.lpszClassName = szWindowClass;

wcex.hIconSm = LoadIcon(wcex.hInstance, MAKEINTRESOURCE(IDI_SMALL));

 

return RegisterClassEx(&wcex);

}

 

// Функция, сохраняющая дескриптор экземпляра приложения и

// создающая главное окно приложения.

BOOL InitInstance(HINSTANCE hInstance, int nCmdShow)

{

HWND hWnd;

 

hInst = hInstance;

 

hWnd = CreateWindow(szWindowClass, szTitle, WS_OVERLAPPEDWINDOW,

CW_USEDEFAULT, 0, CW_USEDEFAULT, 0, NULL, NULL, hInstance, NULL);

 

if (!hWnd) {

return FALSE;

}

 

ShowWindow(hWnd, nCmdShow);

UpdateWindow(hWnd);

 

return TRUE;

}

 

// Функция, вычисляющая значение х и у координат точки на кривой.

// Принимает в качестве параметров вектор-массив точек и

// параметр t, характеризующий положение на кривой.

POINT CalcBezierCurve(vector
pts, const double& t)

{

int i, c;

double p;

POINT np;

int n = static_cast(pts.size()) - 1;

 

c = 1;

for (i = 0; i <= n; i++) {

pts[i].x = pts[i].x * c;

pts[i].y = pts[i].y * c;

c = (n-i)*c/(i+1);

}

p = 1;

for (i = 0; i <= n; i++) {

pts[i].x = pts[i].x * p;

pts[i].y = pts[i].y * p;

p = p * t;

}

p = 1;

for (i = n; i >= 0; i--) {

pts[i].x = pts[i].x * p;

pts[i].y = pts[i].y * p;

p = p * (1-t);

}

np.x = 0;

np.y = 0;

for (i = 0; i <= n; i++) {

np.x = np.x + pts[i].x;

np.y = np.y + pts[i].y;

}

return np;

}

 

// Процедура отрисовки кривой Безье.

// Принимает в качестве параметров дескриптор контекста устройства и

// вектор-массив точек, по которым ведется построение кривой.

void DrawBezier(HDC hdc, vector
pts)

{

double t; // Параметр, по которому будет идти вычисление точек на кривой: t = [0,...,1].

 

HPEN hPen; // Дескриптор пера, которым будем пользоваться для сохранения

// разных стилей рисования линий для построения как отрезков, соединяющих

// точки массива, так и самой кривой.

 

POINT np = {0, 0}; // Точка, в которую будет заноситься результат выполнения функции CalcBezierCurve.

 

// Перемещаем текущую позицию пера в первую точку массива.

MoveToEx(hdc, pts[0].x, pts[0].y, NULL);

 

// Присваиваем перу характеристику: пунктирная линия, толщина - 1 пиксель, синий цвет.

hPen = CreatePen(PS_DASH, 1, RGB(0, 10, 170));

 

SelectObject(hdc, hPen); // Выбираем объект нашего пера в контекст устройства.

 

// Строим пунктирные линии, соединяющие точки массива.

for (int i = 0; i < pts.size(); i++)

LineTo(hdc, pts[i].x, pts[i].y);

 

// Присваиваем перу характеристику: сплошная линия, толщина - 2 пикселя, темно-красный цвет.

hPen = CreatePen(PS_SOLID, 2, RGB(200, 50, 10));

 

SelectObject(hdc, hPen); // Выбираем объект нашего пера в контекст устройства.

 

// Перемещаем текущую позицию пера в первую точку массива.

MoveToEx(hdc, pts[0].x, pts[0].y, NULL);

 

// Цикл отрисовки кривой Безье.

// Для параметра t, пробегающего от 0 до 1 с шагом 0.3 (данный шаг обеспечивает умеренную сглаженость кривой)

// вычисляем значение новой точки и строим линию, соединяющую предыдущую точку с новой.

for (t = 0.0; t < 1.0; t += 0.03) {

np = CalcBezierCurve(pts, t);

LineTo(hdc, np.x, np.y);

}

LineTo(hdc, pts.back().x, pts.back().y);

 

// Возвращаем стандартное перо в контекст устройства.

SelectObject(hdc, (HPEN)GetStockObject(BLACK_PEN));

// Рисуем окружности, выделяющие точки массива.

for (int i = 0; i < pts.size(); i++)

Ellipse(hdc, pts[i].x-5, pts[i].y-5, pts[i].x+5, pts[i].y+5);

}

// Функция, возвращающая номер точки массива,

// по которой пользователь щелкает мышью.

// Принимает в качестве параметров х и у координаты точки щелчка

// и вектор-массив точек, задающих кривую.

int GetNumberOfPoint (int x, int y, vector
P)

{

int lim = static_cast(P.size());

// Проходим по массиву точек,

for (int i = 0; i < lim; i++) {

// Если щелчок произвелся по точке или в непосредственной близости от нее, то

if ((x > P[i].x-15 && x < P[i].x+15) && (y > P[i].y-15 && y < P[i].y+15))

// возвращаем номер этой точки (индекс в массиве).

return i;

}

// Если щелчок произвелся не по точке массива, возвращаем отрицательное число.

return -1;

}

 

 // Оконная процедура, обеспечивающая обработку сообщений для основного окна программы.

LRESULT CALLBACK WndProc(HWND hWnd, UINT message, WPARAM wParam, LPARAM lParam)

{

 

static bool IsSelected = false; // Булевская переменная, служащая для распознания, выбран ли набор точек

// для кривой или еще нет. Начальное значение - "ложь", не выбран.

 

static vector
pts; // Вектор-массив точек, по которым будем строить кривую.

 

PAINTSTRUCT ps;

HDC hdc; // Контекст устройства.

 

switch (message) // Обработка текущего сообщения.

{

case WM_LBUTTONDOWN:

// Нажата левая кнопка мыши.

// Если точки еще не выбраны, заносим координаты точки в массив и

// рисуем окружность для выделения места нажатия.

if (!IsSelected) {

hdc = GetDC(hWnd);

 

POINT tmp;

tmp.x = LOWORD(lParam);

tmp.y = HIWORD(lParam);

pts.push_back(tmp);

 

Ellipse(hdc, pts.back().x-5, pts.back().y-5, pts.back().x+5, pts.back().y+5);

 

ReleaseDC(hWnd, hdc);

}

break;

 

case WM_MOUSEMOVE:

// Сообщение от перемещения мыши, обрабатывается только тогда, когда выбран набор точек и

// после отрисовки кривой (выбран пункт меню "Draw curve").

if (IsSelected) {

// Если при перемещении мыши нажата левая кнопка,

if (wParam && MK_LBUTTON) {

hdc = GetDC (hWnd);

 

// то находим номер точки массива, если щелчок произвелся по одной из его точек.

int mnp = GetNumberOfPoint(LOWORD(lParam), HIWORD(lParam), pts);

if (mnp < 0) break;

 

// Заносим в точку массива с номером выбранной точки новые координаты.

pts[mnp].x = LOWORD (lParam) ;

pts[mnp].y = HIWORD (lParam) ;

 

// Посылаем сообщение для перерисовки клиентской обдасти окна, и, следовательно, самой кривой.

SendMessage(hWnd, WM_PAINT, NULL, NULL);

ReleaseDC (hWnd, hdc);

}

}

break;

 

case WM_COMMAND:

// Обработка сообщений, поступающих при выборе пунктов меню.

 

switch (LOWORD(wParam)) // Обработка значения идентификатора пункта меня.

{

case IDM_EXIT:

// Меню File -> Exit

// Выход.

DestroyWindow(hWnd);

break;

case ID_CURVE_DRAWCURVE:

// Меню Curve -> Draw curve

// Если размер массива точек равен нулю, т. е. пользователь не выбрал ни одной точки, то

// выводим сообщение об ошибке.

if (pts.size() == 0) {

MessageBox(hWnd, "There is necessary to put at least one point to client area of window!",

"An error occured!", NULL);

break;

}

// Иначе - присваиваем переменной IsSelected значение "истина" (означающая, что пользователь выбрал набор точек)

IsSelected = true;

// и осуществляем перерисовку.

SendMessage(hWnd, WM_PAINT, NULL, NULL);

break;

case ID_CURVE_NEWCURVE:

// Меню Curve -> New curve

// Очищаем массив точек, IsSelected присваиваем "ложь" и осуществляем перерисовку.

for (int i = pts.size(); i > 0; i--)

pts.pop_back();

IsSelected = false;

SendMessage(hWnd, WM_PAINT, NULL, NULL);

break;

default:

return DefWindowProc(hWnd, message, wParam, lParam);

}

break;

 

case WM_PAINT:

// Перерисовка клиенской области окна.

  // Объявление всей клиентской области подлежащей перерисовке.

InvalidateRect(hWnd, NULL, TRUE);

  hdc = BeginPaint(hWnd, &ps);

  // Если массив точек не пуст, то рисуем кривую по данным точкам.

if (pts.size() != 0)

DrawBezier(hdc, pts) ;

 

EndPaint(hWnd, &ps);

break;

 

case WM_DESTROY:

// Выход.

PostQuitMessage(0);

break;

 

default:

return DefWindowProc(hWnd, message, wParam, lParam);

}

 

return 0;

}
3. Закраска области заданным цветом

Рассмотрим область, ограниченную набором пикселей заданного цвета и точку (x, y), лежащую внутри этой области.

Задача заполнения области заданным цветом в случае, когда эта область не является выпуклой, может оказаться довольно сложной.

Простейший рекурсивный алгоритм:

 

void PixelFill(int x, int y, int border_color, int color)

{

int c = getpixel(x, y);

if ((c != border_color) && (c != color))

{

putpixel(x, y, color);

PixelFill(x – 1, y, border_color, color);

PixelFill(x + 1, y, border_color, color);

PixelFill(x, y – 1, border_color, color);

PixelFill(x, y + 1, border_color, color);

}

}

 Этот алгоритм является слишком неэффективным, так как для всякого уже отрисованного пикселя функция вызывается ещё 4 раза и, кроме того, этот алгоритм требует слишком большого объёма стека из-за большой глубины рекурсии. Поэтому для решения задачи закраски области предпочтительнее алгоритмы, способные обрабатывать сразу целые группы пикселей, т. е. использовать их «связность». Если данный пиксель принадлежит области, то, скорее всего, его ближайшие соседи также принадлежат данной области.

Группой таких пикселов обычно выступает полоса, определяемая правым пикселем. Для хранения правых определяющих пикселов используется стек. Словесно опишем улучшенный алгоритм, использующий когерентность пикселов.

Сначала заполняется горизонтальная полоса пикселов, содержащих начальную точку. Затем, чтобы найти самый правый пиксель каждой строки, справа налево проверяется строка, предыдущая по отношению к только что заполненной полосе. Адреса найденных пикселов заносятся в стек. То же самое выполняется и для строки, следующей и за последней заполненной полосой. Когда строка обработана таким способом, в качестве новой начальной точки используется пиксель, адрес которого берется из стека. Для него повторяется вся описанная процедура. Алгоритм заканчивает свою работу, если стек пуст.
Используемые источники

http://www.opita.net/node/699

http://www.opita.net/node/50

http://compgraph.tpu.ru/region.htm