Обработка результатов косвенных измерений.. Лабораторная работа 7 Обработка результатов косвенных измерений. Никитюк М. Ю. Группа 2зк2 Проверил Норин В. А
 Скачать 53.86 Kb. Скачать 53.86 Kb.
|
|
Санкт-Петербургский государственный архитектурно-строительный университет Лабораторная работа № 7 «Обработка результатов косвенных измерений.» Выполнила: Никитюк М.Ю. Группа: 2-ЗК-2 Проверил: Норин В.А. Санкт-Петербург 2017 Цель лабораторной работы – обработка результатов косвенного измерения. Обработка результатов косвенного измерения При косвенных измерениях физическая величина Y, значение корой надо определить, является известной функцией fряда других величин – аргументов x1, x2 . . . xn. Данные аргументы находятся прямыми многократными измерениями, а величина Y вычисляется по формуле: Y = f(x1, x2, . . ., xn) В качестве результата косвенного измерения рассматривают оценку величины Y, определяемую подстановкой в (1) оценок аргументов этой функции. Каждый из аргументов измеряется в результате прямых многократных измерений с некоторой погрешностью ∆x, вносящей определенный вклад в результат косвенного измерения. Полагая, что погрешности ∆xмалы, можно записать 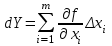 , , где каждое слагаемое 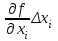 представляет собой частную погрешность результата косвенного измерения, вызванную погрешностью ∆xизмерения величины xi . Частные производные носят название коэффициентов влияния соответствующих погрешностей. представляет собой частную погрешность результата косвенного измерения, вызванную погрешностью ∆xизмерения величины xi . Частные производные носят название коэффициентов влияния соответствующих погрешностей.Результаты измерений L(длины), B( ширины), H(высоты) . L
B
H
Определяются оценки результатов измерения 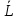 , ,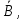 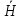 среднего квадратического отклонения результатов измерения SL , SB, SH среднего квадратического отклонения результатов измерения SL , SB, SH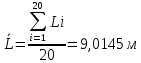 SL SL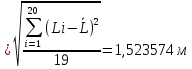 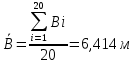 SB SB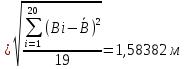 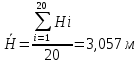 SH SH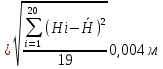 Исключаются грубые погрешности: Производим проверку наличия грубых погрешностей в результатах измерения по критерию Диксона. Составляется вариационный возрастающий ряд из результатов измерений для величины L: 8,747;8,750;8,751;8,752;8,753;8,754;8,755;8,757;8,759; 9,265;9,285. Для крайнего члена этого ряда 9,285 м расчетный критерий Диксона: Кд= 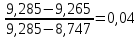 По этому критерию результат 9,265 не является промахом при уровне значимости q=0,02 и не отбрасывается . (0,04<0,3) По этому критерию результат 9,265 не является промахом при уровне значимости q=0,02 и не отбрасывается . (0,04<0,3) Составляется вариационный возрастающий ряд из результатов измерений для величины B:6,188; 6,188;6,196;6,198;6,19;6,191;6,192;6,193;6,194;6,195;6,721 Для крайнего члена этого ряда 6,186 м расчетный критерий Диксона: Кд= 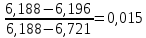 По этому критерию результат 6,188 не является промахом при уровне значимости q=0,015 и не отбрасывается . (0,015<0,3) По этому критерию результат 6,188 не является промахом при уровне значимости q=0,015 и не отбрасывается . (0,015<0,3) Составляется вариационный возрастающий ряд из результатов измерений для величины H: 3,054;3,055;3,057;3,059;3,060;3,062. Для крайнего члена этого ряда 3,062 м расчетный критерий Диксона: Кд= 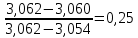 По этому критерию результат 3,069 не является промахом при уровне значимости q=0,05 и не отбрасывается . (0,25<0,3) По этому критерию результат 3,069 не является промахом при уровне значимости q=0,05 и не отбрасывается . (0,25<0,3) Проверяется гипотеза о нормальности распределения для всех серий результатов наблюдений по составному критерию. Проверяя критерий 1, вычисляются отношения: 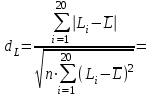 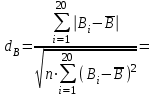 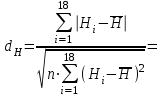 Задав доверительную вероятность P1 = 0,98 и для уровня значимости q1 = 1 – Р1=0,02, по табл. 9 определяют квантили распределения 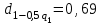 и и 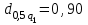 (для n=20) и (для n=20) и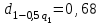 и и 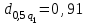 (для n=18) . Сравнивают dL,dB и dH с (для n=18) . Сравнивают dL,dB и dH с 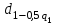 и и 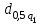 . Так как . Так как 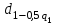 <dL, dB , dH < <dL, dB , dH < 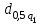 , то гипотеза о нормальном законе распределения вероятности результата измерения для обеих серий согласуется с экспериментальными данными. , то гипотеза о нормальном законе распределения вероятности результата измерения для обеих серий согласуется с экспериментальными данными.Проверяя критерий 2, задают доверительную вероятность Р2 = 0,98 и для уровня значимости q2 = 1 – Р2 с учетом n= 20(Для L и B) и n=18(для H) определяют по табл. 10 значения m1 = m2 =m3= 1 и Р1* = P2* =P3* = 0,99. Для вероятности Р* = 0,99 из таблицы 12 определяют значение Zp/2= 2,58 и рассчитывают: ЕL = Zp/2 SL = ЕB = Zp/2 SB = ЕH= Zp/2SH = Так как не более одной разности | 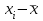 | превосходит эти значения по трем сериям, то гипотеза о нормальном законе распределения вероятности результата измерения согласуется с экспериментальными данными. | превосходит эти значения по трем сериям, то гипотеза о нормальном законе распределения вероятности результата измерения согласуется с экспериментальными данными.Следовательно, гипотеза о нормальности распределения данных подтверждается. Уровень значимости составного критерия: q≤0,02+0,02=0,04, т.е гипотеза о нормальности распределения результатов измерения подтверждается при уровне значимости не более 0,04. Определяется оценка среднего  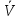  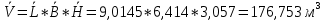 Находятся частные погрешности результата косвенного измерения 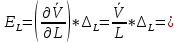 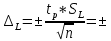 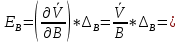 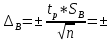 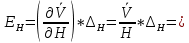 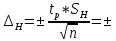 Находится суммарная погрешность результата косвенного измерения 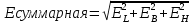 = = Записывается окончательный результат: 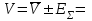 м, nL= 20, nB= 20,nH= 20 ,Pд= 0.95. м, nL= 20, nB= 20,nH= 20 ,Pд= 0.95. |

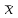 )2
)2