Главная страница
Навигация по странице:

  • Выборочное распределение служащих компании по сумме начислений на заработную плату (д.е.) представлено в таблице

  • Вариант – 2,4,7.

  • Вариант – 3,6,8,10.

  • ПРОВЕРКА ГИПОТЕЗЫ О НОРМАЛЬНОМ РАСПРЕДЕЛЕНИИ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ Задание 1.

    		•

    ПОСА_лаб.7. Лабораторная работа 7 проверка гипотезы о числовом значении математического ожидания задание Вариант 1,5,9


    Скачать 174.5 Kb.
    НазваниеЛабораторная работа 7 проверка гипотезы о числовом значении математического ожидания задание Вариант 1,5,9
    Дата13.04.2021
    Размер174.5 Kb.
    Формат файлаdoc
    Имя файлаПОСА_лаб.7.doc
    ТипЛабораторная работа
    #194126

    Лабораторная работа № 7

    ПРОВЕРКА ГИПОТЕЗЫ О ЧИСЛОВОМ ЗНАЧЕНИИ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ

    Задание 1.

    Вариант -1,5,9.

    Выборочное распределение служащих компании по сумме начислений на заработную плату (д.е.) представлено в таблице:
    3-5
    5-7
    7-9
    9-11
    11-13



    7
    26
    39
    35
    13

    На уровне значимости 0,05 проверить нулевую гипотезу о том, что средняя сумма начислений всех служащих компании равна 8,25, при альтернативной гипотезе – средняя сумма начислений больше 8,25.

    Вариант – 2,4,7.

    Выборочное распределение работников компании по показателям работоспособности (в баллах) представлено в таблице:
    5-6
    6-7
    7-8
    8-9
    9-10



    16
    39
    37
    11
    7

    На уровне значимости 0,05 проверить нулевую гипотезу о том, что средний показатель работоспособности всех работников компании равен 7,95, при альтернативной гипотезе – средний показатель работоспособности меньше 7,95.

    Вариант – 3,6,8,10.

    Выборочное распределение работников компании по показателям работоспособности (в баллах) представлено в таблице:
    4-5
    5-6
    6-7
    7-8
    8-9
    9-10



    6
    12
    24
    13
    7
     3

    На уровне значимости 0,01 проверить нулевую гипотезу о том, что средний показатель работоспособности всех работников компании равен 6,15, при альтернативной гипотезе – средний показатель работоспособности не равен 6,15.
    ПРОВЕРКА ГИПОТЕЗЫ

    О НОРМАЛЬНОМ РАСПРЕДЕЛЕНИИ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ

    Задание 1. При уровне значимости 0,05 проверить гипотезу о нормальном распределении генеральной совокупности c помощью критерия , если известны эмпирические и теоретические частоты:

    Эмпирические частоты

    6
    13
    38
    74
    106
    85
    30
    14

    Теоретические частоты

    3
    14
    42
    82
    99
    76
    37
    13

    Указание:

    1. вычислите наблюдаемое значение критерия по формуле ;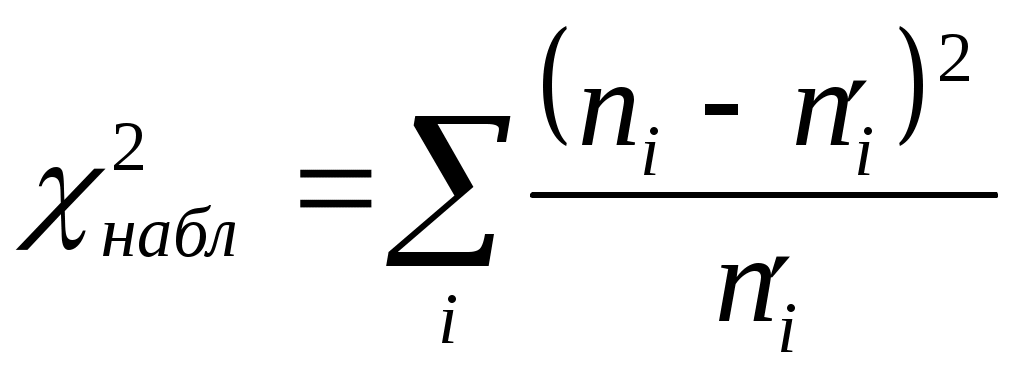

    Проверьте себя: .

    Критерий согласия Пирсона (χ2) применяют для проверки гипотезы о соответствии эмпирического распределения предполагаемому теоретическому распределению F(x) при большом объеме выборки (n ≥ 100). Критерий применим для любых видов функции F(x), даже при неизвестных значениях их параметров, что обычно имеет место при анализе результатов механических испытаний. В этом заключается его универсальность.

    Использование критерия χ2 предусматривает разбиение размаха варьирования выборки на интервалы и определения числа наблюдений (частоты) nj для каждого из e интервалов. Для удобства оценок параметров распределения интервалы выбирают одинаковой длины.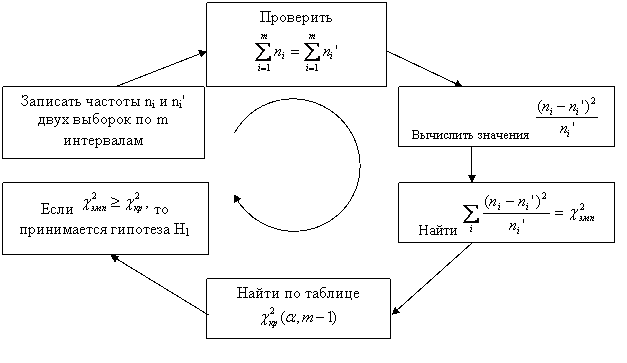



    1. найдите , где число степеней свободы , s – число групп (интервалов), r – число параметров предполагаемого распределения (для нормального распределения оценивают два параметра: математическое ожидание и среднее квадратическое отклонение) с помощью функции =ХИ2ОБР(0,05;5).

    Проверьте себя: .

    3) сделайте вывод о справедливости гипотезы о нормальном распределении генеральной совокупности.
    Задание 2. В ходе обследования состояния здоровья населения было произведено измерение роста по выборке из 250 человек. Соответствующие данные хранятся в файле Lr_7.xls  на вкладке "Рост". При уровне значимости 0,05 проверить гипотезу о нормальном распределении генеральной совокупности c помощью критерия .

    Указание:

    1. разбейте весь интервал наблюдаемых значений случайной величины Х – рост, см. на частичные интервалы одинаковой длины и вычислите число вариант, попавших в каждый интервал. Воспользуйтесь результатами лабораторной работы №3: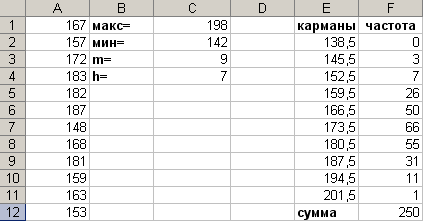



    1. поместите результаты вычислений в таблицу:

      Границы интервалов
      Частота







      138,5
      145,5
      3

      145,5
      152,5
      7

      152,5
      159,5
      26

      159,5
      166,5
      50

      166,5
      173,5
      66

      173,5
      180,5
      55

      180,5
      187,5
      31

      187,5
      194,5
      11

      194,5
      201,5
      1

    2. найдите середины интервалов ;

    3. вычислите выборочную среднюю и выборочное среднее квадратическое отклонение и (см. лабораторную работу №4). Проверьте себя: ,

    4. вычислите концы интервалов : , . Наименьшее значение z, т.е. полагают равным минус бесконечности, а наибольшее, т.е. – плюс бесконечности.

    5. вычислите теоретические вероятности попадания Х в интервалы по равенству

    ,

    где – функция Лапласа. Учтите, что , .

    Для вычисления значения необходимо вызвать встроенную функцию НОРМСТРАСП(z) и из полученного результата вычесть 0,5.

    1. найдите теоретические частоты . Если все сделано верно, у Вас получится таблица:

      Границы

      интервалов
      Частота


      Границы

      интервалов






























      138,5
      145,5
      3
      142


      -2,3952
      -0,5
      -0,4917
      0,0083
      2,08

      145,5
      152,5
      7
      149
      -2,3952
      -1,7254
      -0,4917
      -0,4578
      0,0339
      8,48

      152,5
      159,5
      26
      156
      -1,7254
      -1,0555
      -0,4578
      -0,3544
      0,1034
      25,84

      159,5
      166,5
      50
      163
      -1,0555
      -0,3856
      -0,3544
      -0,1501
      0,2043
      51,07

      166,5
      173,5
      66
      170
      -0,3856
      0,2842
      -0,1501
      0,1119
      0,2620
      65,50

      173,5
      180,5
      55
      177
      0,2842
      0,9541
      0,1119
      0,3300
      0,2181
      54,52

      180,5
      187,5
      31
      184
      0,9541
      1,6239
      0,3300
      0,4478
      0,1178
      29,46

      187,5
      194,5
      11
      191
      1,6239
      2,2938
      0,4478
      0,4891
      0,0413
      10,32

      194,5
      201,5
      1
      198
      2,2938


      0,4891
      0,5
      0,0109
      2,73









      170,53


























      10,45


















    2. вычислите . Проверьте себя: :

    3. найдите . Проверьте себя: .

    4. сделайте вывод о справедливости гипотезы о нормальном распределении генеральной совокупности.


    Задание 3. Перейдите на вкладку с номером Вашего варианта файла Lr_7.xls. При уровне значимости 0,05 проверьте гипотезу о нормальном распределении генеральной совокупности c помощью критерия .

    написать администратору сайта