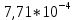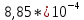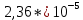Лаба 8 Маятник Максвелла. Отчет. Лабораторная работа 8 маятник максвелла цель работы определение момента инерции маятника Максвелла. Задание к работе
 Скачать 89.45 Kb. Скачать 89.45 Kb.
|
|
Лабораторная работа № 1.8 МАЯТНИК МАКСВЕЛЛА Цель работы: определение момента инерции маятника Максвелла. Задание к работе: К работе допущен: Расчеты выполнил: Работу защитил: Введение Момент инерции твердого тела – важная физическая характеристика. Он является мерой инертности тела при вращательном движении. Момент инерции твердого тела J относительно оси вращения равен сумме произведений элементарных масс Δ 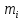 твердого тела на квадрат их расстояний твердого тела на квадрат их расстояний 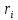 от оси: от оси: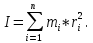 Маятник Максвелла представляет собой массивный диск 1, насаженный на стержень 2 и подвешенный бифилярно с помощью нитей 3 к горизонтальной опоре (рис. 1). Если, накрутив нити на концы стержня, поднять маятник на некоторую высоту h (рис. 1) относительно положения равновесия 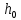 (крайнего нижнего положения) и отпустить, то маятник начнет поступательное движение вниз, одновременно вращаясь вокруг оси симметрии. При этом запасенная им потенциальная энергия будет переходить в кинетическую энергию поступательного и вращательного движения. Достигнув положения равновесия, маятник, у которого потенциальная энергия полностью перешла в кинетическую, не остановится. Он по инерции будет продолжать вращение, нити начнут наматываться на стержень, и маятник вновь поднимется вверх. Однако из-за убыли механической энергии, вследствие трения нитей о стержень и сопротивления воздуха, расстояние, пройденное маятником при подъеме, окажется меньше, чем при спуске. Поэтому колебательное движение маятника (движение вниз и вверх) оказывается затухающим. (крайнего нижнего положения) и отпустить, то маятник начнет поступательное движение вниз, одновременно вращаясь вокруг оси симметрии. При этом запасенная им потенциальная энергия будет переходить в кинетическую энергию поступательного и вращательного движения. Достигнув положения равновесия, маятник, у которого потенциальная энергия полностью перешла в кинетическую, не остановится. Он по инерции будет продолжать вращение, нити начнут наматываться на стержень, и маятник вновь поднимется вверх. Однако из-за убыли механической энергии, вследствие трения нитей о стержень и сопротивления воздуха, расстояние, пройденное маятником при подъеме, окажется меньше, чем при спуске. Поэтому колебательное движение маятника (движение вниз и вверх) оказывается затухающим.  Рис.1. Маятник Максвелла Определение момента инерции маятника Максвелла в данной лабораторной работе основано на использовании закона сохранения механической энергии. 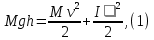 где М – масса маятника; v – скорость поступательного движения центра масс маятника;  – угловая скорость вращения маятника; I – момент инерции маятника. – угловая скорость вращения маятника; I – момент инерции маятника.Решая уравнение (1) относительно I, получаем: 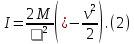 Поскольку поступательное движение центра масс маятника равноускоренное, то при нулевой начальной скорости: 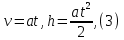 где t – время, за которое маятник опустился с высоты h до нижнего положения. Если считать, что раскручивание нитей со стержня происходит без проскальзывания, то угловая скорость связана с линейной скоростью центра масс маятника соотношением: 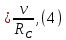 где 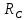 – радиус стержня. – радиус стержня.Подставляя (3) и (4) в (2), получаем выражение для определения момента инерции маятника, содержащее параметры, которые можно определить опытным путем: 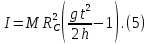 Таким образом, измерив массу маятника М, радиус стержня 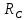 и время t падения маятника с высоты h, по формуле (5) можно экспериментально определить момент инерции маятника Максвелла. и время t падения маятника с высоты h, по формуле (5) можно экспериментально определить момент инерции маятника Максвелла.По свойству аддитивности момент инерции маятника I равен сумме моментов инерции диска 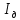 , стержня , стержня 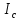 и сменных колец и сменных колец 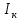 : :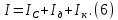 Так как маятник состоит из тел правильной формы, моменты инерции которых известны, формулу (6) можно представить в виде: 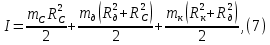 где 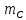 , , 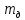 , и , и 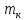 – массы стержня, диска и сменного кольца соответственно; – массы стержня, диска и сменного кольца соответственно; 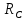 , , 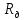 , и , и 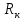 соответствующие радиусы. соответствующие радиусы.Таким образом, зная массы диска, стрежня, сменных колец и их радиусы по формуле (7) можно теоретически вычислить момент инерции маятника. 1. Описание установки Установка включает в себя маятник Максвелла, электронный блок и набор сменных колец. Общий вид установки представлен на рис.2. 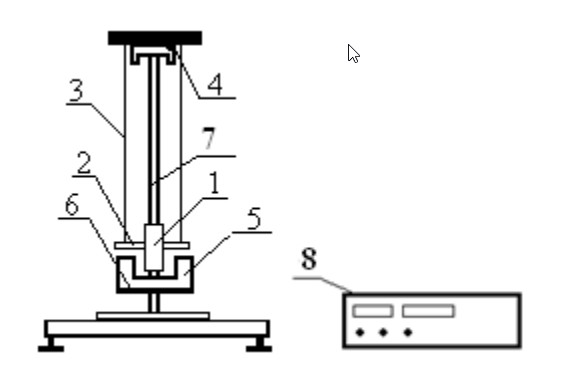 Рис.2. Общий вид установки Маятник представляет собой диск 1 закрепленный на стержне 2, подвешенный на бифилярном подвесе 3. На диск крепятся сменные кольца. Установка состоит из основания, на вертикальной стойке которого размещены верхний 4 и подвижный нижний 5 кронштейны. Верхний кронштейн 4 снабжен устройством для крепления и регулировки подвеса 3. На вертикальной стойке нанесена миллиметровая шкала 7, по которой определяют высоту h. В кронштейне 5 закреплен фотоэлектрический датчик, фиксирующий положение маятника в нижнем положении, по достижении которого останавливается счетчик времени. На передней панели электронного блока 8 имеются индикаторы единиц измерения и времени, кнопки управления: «СБРОС», «СТОП» и «ПУСК». Технические характеристики установки: Масса стержня 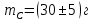 ; радиус стержня ; радиус стержня 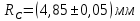 . .Масса диска 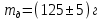 ; радиус диска ; радиус диска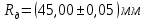 . .Массы сменных колец 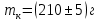 , , 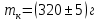 ; внешний радиус сменных колец ; внешний радиус сменных колец 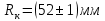 . .2. Порядок выполнения измерений Упражнение 1. Определить массу маятника без сменного кольца М. Результат записать в табл. 1. Установить между фотодатчиками, находящимися в кронштейнах 4 и 5, расстояние L заданное преподавателем при помощи шкалы 10. Вычислить расстояние h: 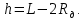 Вращая маятник, зафиксировать его в исходном верхнем положении. Одновременно отпустить маятник и нажать кнопку «ПУСК» на электронном блоке, произвести отсчет времени t. Занести результаты измерений в табл. 1. Повторить п.2 заданное преподавателем количество раз. Таблица 1
Упражнение 2. Надеть на диск сменное кольцо, масса которого задана преподавателем. Определить массу получившегося маятника М. Результат записать в табл. 2 Вычислить расстояние h: 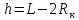 Вращая маятник, зафиксировать его в исходном верхнем положении. Одновременно отпустить маятник и нажать кнопку «ПУСК» на электронном блоке, произвести отсчет времени t. Занести результаты измерений в табл. 2. Повторить п.2 заданное преподавателем количество раз. Таблица 2
3. Обработка результатов измерений 3.1. Рассчитать среднее время движения маятника можно по формуле: 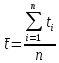 Значения времени, полученного в результате первого и второго опыта в упр. 1 считаю как промах и не учитываю при вычислении. 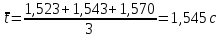 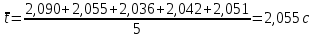 3.2. По формуле (5) можно рассчитать момент инерции маятника 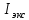 : :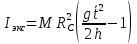 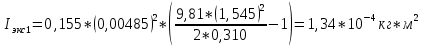 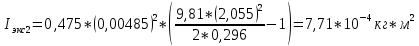 3.3. Вычислить абсолютную ошибку времени, абсолютную и относительную ошибки момента инерции можно по формулам: 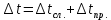 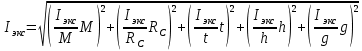 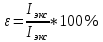 3.3.1. Сначала вычислю абсолютную погрешность времени. 3.3.1.1. Погрешность прибора можно определить по цене деления. Так как прибор измеряет время с точностью до 1 мс, то 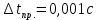 . .3.3.1.2. Случайная погрешность определяется по формуле: 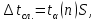 где 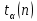 – коэффициент Стьюдента, S - средняя квадратичная погрешность среднего арифметического. – коэффициент Стьюдента, S - средняя квадратичная погрешность среднего арифметического.Следовательно, перед началом вычислений надо найти недостающие величины. 3.3.1.2.1. Коэффициент Стьюдента ( 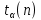 ) равен 2,9 при α=0,9 и n=3, равен 2,1 при α=0,9 и n=5. ) равен 2,9 при α=0,9 и n=3, равен 2,1 при α=0,9 и n=5.3.3.1.2.2. S вычисляется по формуле: 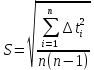 Δ 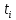 вычисляется по формуле: вычисляется по формуле:Δ 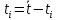 , ,следовательно: Δ 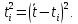 Δ 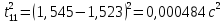 Δ 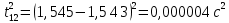 Δ 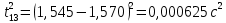 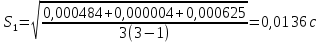 Δ 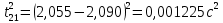 Δ 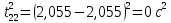 Δ 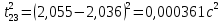 Δ 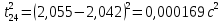 Δ 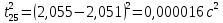 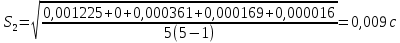 3.3.1.2.3. Теперь можно вычислить 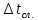 : :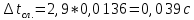 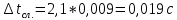 3.3.1.3. Абсолютная погрешность равна: 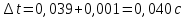 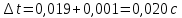 3.3.2. Теперь вычислю абсолютную погрешность момента инерции. Так как g – табличная величина, то в качестве абсолютной погрешности принимается половина разряда последней значащей цифры числа, т.е. 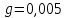 . .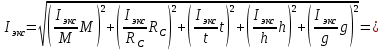 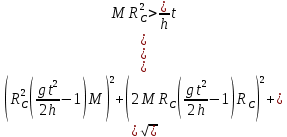 Для упр. 1: 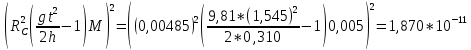 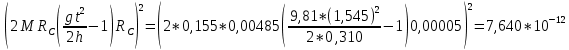 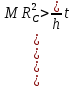 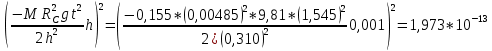 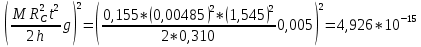 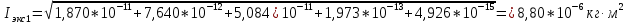 Для упр. 2: 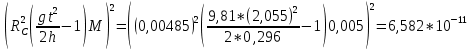 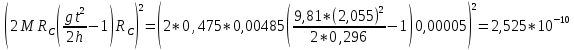 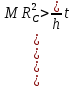 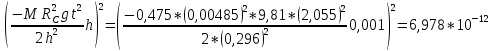 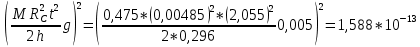 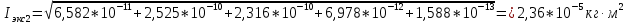 3.3.3. Теперь вычислю относительную погрешность момента инерции. 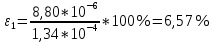 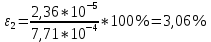 3.4. По формуле (7) можно рассчитать теоретический момент инерции маятника 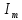 : :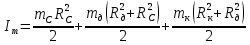 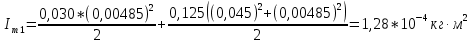 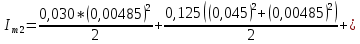 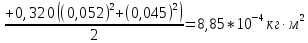 3.5. Сравниваю экспериментальное и теоретическое значения момента инерции, вычислив разницу между ними в процентах: 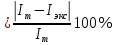 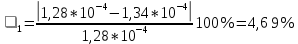 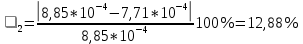 3.6. На основе полученных экспериментальных значений рассчитаю момент инерции кольца 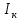 по формуле (6): по формуле (6):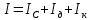 откуда 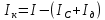 Так как значение 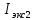 получено в ходе эксперимента с использованием кольца, стержня и диска, то его значение можно принять как I, и так как получено в ходе эксперимента с использованием кольца, стержня и диска, то его значение можно принять как I, и так как 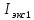 получено с использованием стержня и диска, но без кольца, то его значение можно принять как получено с использованием стержня и диска, но без кольца, то его значение можно принять как 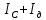 : :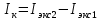 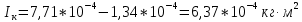 3.7. На основе полученных теоретический значений рассчитаю момент инерции кольца 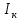 по формуле: по формуле: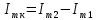 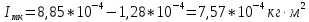 3.8. Сравниваю экспериментальное и теоретическое значения момента инерции кольца, вычислив разницу между ними в процентах: 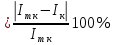 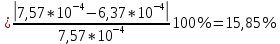 Заключение Определил момент инерции маятника Максвелла. Для этого рассчитал теоретические значения инерции и провел опыты, чтобы рассчитать экспериментальные значения: 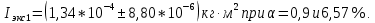 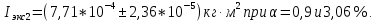 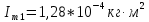 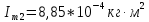 Также вычислил теоретическое и экспериментальное значение инерции кольца: 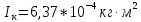 – экспериментальное – экспериментальное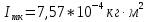 – теоретическое – теоретическое |

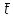 ,
,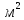
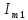 ,
,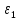 ,%
,%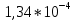
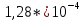
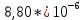
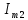 ,
, ,%
,%