Лабораторная работа 8 Популяция

Название	Лабораторная работа 8 Популяция
Дата	03.11.2021
Размер	204 Kb.
Формат файла
Имя файла	18_MaksimovDaniil_08.doc
Тип	Лабораторная работа #262591

Лабораторная работа №8

Популяция

1.Постановка задачи

Необходимо рассмотреть процесс изменения популяризации города (планеты). В изменении популяризации участвуют два процесса: гибель и рождаемость. необходимо рассмотреть несколько вариантов зависимости размера населения от различных заданных первичных параметров.

2.Идеализация

Не учитываем среду обитания
Не учитываем ресурсы
Не учитываем несистематизированное изменение популяризации, такое как, например, гибель населения от катастроф

3.Модель Мальтуса

3.1.Теория

Введём параметры:

n(t) - зависимость населения от времени.

α - характеристика рождаемости

ß - характеристика смертности

Обе характеристики таковы, что: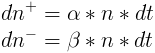

Введём зависимость dn от dt — прирост популяции за короткий промежуток времени

Для получения зависимости n(t) необходимо, очевидно, чтобы dt стремилось к нулю.

Получаем дифференциальное уравнение

Решаем его:

При решении этого уравнения мы предположили, что в начальный момент времени население составляло n0 человек. Получили экспоненциальную зависимость. Рассмотрим её влияние, смоделировав эту зависимость

3.2.Код Matlab

z1.m

global alpha betta n0 np;
np=100;
n0=100;
alpha=0.9;
betta=0.5;%n/n0;
startt=0;
maxt=7;
starty=100;
colors=['b','r','g','y','m','c','k'];
experiments=7;
alphas=alpha:-0.1:alpha-0.1*experiments;
p=zeros(experiments);
for i=1:experiments
%if (i<=experiments/2)
alpha=alphas(i);
%end;
t=[startt maxt];
[t,Y]=ode45('func',t,n0);
Y=Y(Y>=0 & Y<=1000 );
t=t(Y>=0 & Y<=1000 );

p(i)=plot(t,Y,colors(mod(i,length(colors))+1));

hold on;
end;
legend1=legend(strcat('a=',num2str(alphas')),'Location','NorthWest');
ylabel popularity;
xlabel time;
grid on;
title(strcat('Модель Мальтуса при b=',num2str(betta), ' (зависимость от a)'));
hold off;

func.m

function f=func(t,y)
global alpha betta n0;
f=(alpha-betta).*y;
end

3.3.Результат Matlab

Зависимость размера популяции от коэффициента alpha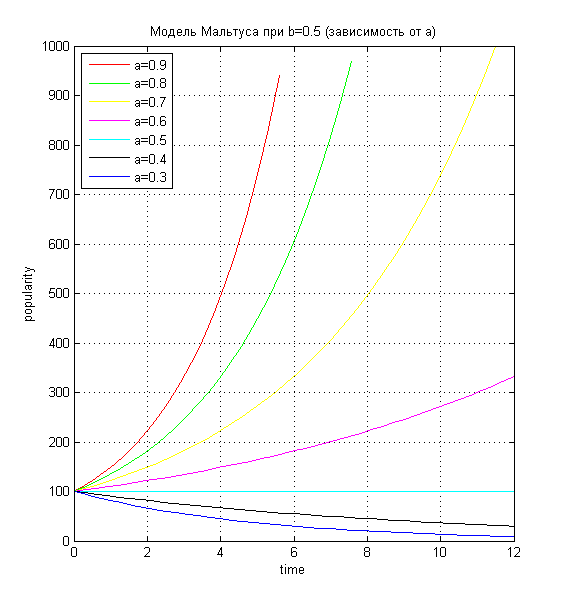

Увеличенно

ОчОчевидно, что данная модель мало похожа на реальное расположение дел на Земле: в зависимости от начальной разницы между α и ß, популяция либо растёт до бесконечности, либо опускается до нуля. Всё, что мы можем делать, это указать начальные значения α и ß.

4.Равновесная численность

4.1.Теория

Пусть у численности населения есть асимптота, равная какой-то установившейся, назовём её равновесной, численности.

Для получения такой модели установим коэффициент рождаемости α, а смертность ß сделаем равной 1-n/np, где np - равновесная численность. В таком случае, чем численность больше равновесной, тем выше смертность населения. Получаем следующее уравнение: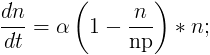

Решим его

Применим начальные условия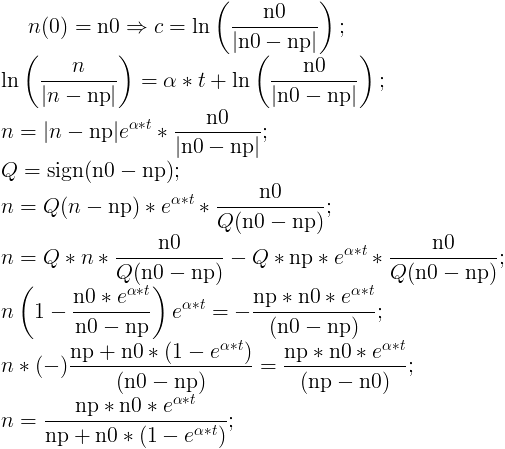

Получили общую формулу, которую можно сразу же проверить в Matlab’е

4.2.Код проверки Matlab

global alpha betta n0 np;
np=400;
n0=800;
alpha=0.2;
betta=0.5;
startt=0;
maxt=12;
colors=['b','r','g','y','m','c','k'];

t=[startt maxt];
[t,Y]=ode45('func2',t,n0);
Y=Y(Y>=0 & Y<=1000 );
t=t(Y>=0 & Y<=1000 );
plot(t,Y,'g');
hold on;
Y2=np*n0*exp(alpha.*t)./(np-n0*(1-exp(alpha.*t)));
plot(t,Y2,'+r');
ylabel popularity;
xlabel time;
grid on;
hold off;

4.3.Результат проверки Matlab

Очевидно, что теоретическое и практическое значение совпадают, однако мы будем использовать экспериментальный способ нахождения популяции (решение задачи Коши)

4.4.Зависимость популяции от α

Код задачи Matlab

func2.m

function f=func2(t,y)
global alpha betta n0 np;
f=alpha*(1-y./np).*y;
end

z2.m

global alpha betta n0 np;
np=100;
n0=400;
alpha=0.4;
betta=0.5;%n/n0;
startt=0;
maxt=12;
starty=100;
colors=['b','r','g','y','m','c','k'];
experiments=7;
alphastep=0.05;
alphas=alpha:-alphastep:alpha-alphastep*experiments;
p=zeros(experiments);
for i=1:experiments
%if (i<=experiments/2)
alpha=alphas(i);
%end;
t=[startt maxt];
[t,Y]=ode45('func2',t,n0);
Y=Y(Y>=0 & Y<=1000 );
t=t(Y>=0 & Y<=1000 );

p(i)=plot(t,Y,colors(mod(i,length(colors))+1));

hold on;
end;
legend1=legend(strcat('a=',num2str(alphas')));

%set(legend1,'Location','NorthWest');
ylabel popularity;
xlabel time;
grid on;
title(strcat('Модель с равновесной численностью, np=',num2str(np),', n0=',num2str(n0), ' (зависимость от a)'));
hold off;

Результат Matlab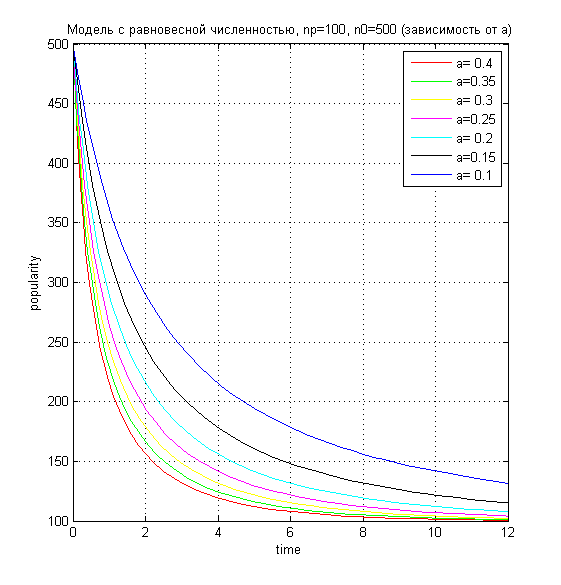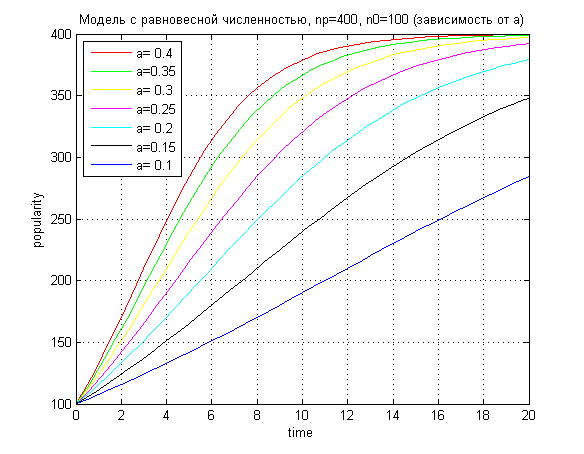

Очевидно, что в зависимости от разницы между текущей популяцией и равновесной, α либо увеличивает скорость стремления к равновесной, либо уменьшает.

4.5.Зависимость популяции от начальной

Код задачи Matlab

z3.m

global alpha betta n0 np;
np=400;
n0=800;
alpha=0.2;
betta=0.5;
startt=0;
maxt=12;
starty=100;
colors=['b','r','g','y','m','c','k'];
experiments=7;
alphastep=0.05;
n0step=100;
n0s=n0:-n0step:n0-n0step*experiments;
p=zeros(experiments);
for i=1:experiments
n0=n0s(i);
t=[startt maxt];
[t,Y]=ode45('func2',t,n0);
Y=Y(Y>=0 & Y<=1000 );
t=t(Y>=0 & Y<=1000 );

p(i)=plot(t,Y,colors(mod(i,length(colors))+1));

hold on;
end;
legend1=legend(strcat('n0=',num2str(n0s')));
%set(legend1,'Location','NorthWest');
ylabel popularity;
xlabel time;
grid on;
title(strcat('Модель с равновесной численностью, np=',num2str(np),', a=',num2str(alpha), ' (зависимость от n0)'));
hold off;

Результат Matlab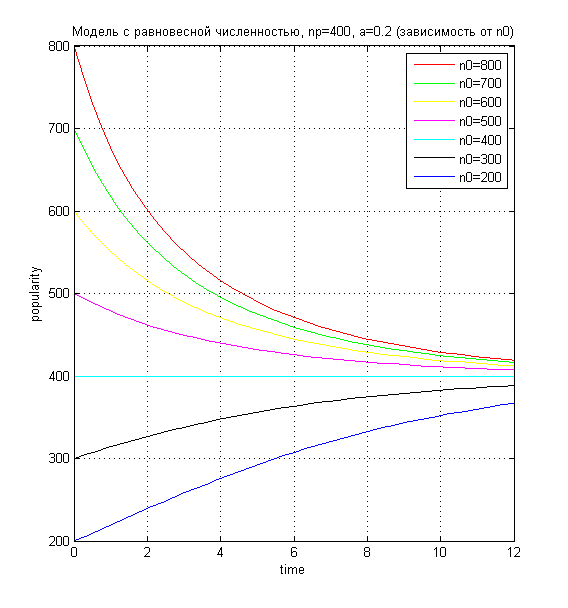

Видно, что размер популяции стремиться стать равновесным, что мы и добивались.

5.Другие распределения

5.1.Sin зависимость

Попробуем внести небольшую погрешность в равновесную модель равновесной численности. Сперва рассмотрим такую зависимость α: α(t)=α*sin(t)^2;

Код Matlab

function f=func2(t,y)
global alpha betta n0 np;
f=alpha.*(sin(t).^2).*(1-y/np).*y;
end

Результат Matlab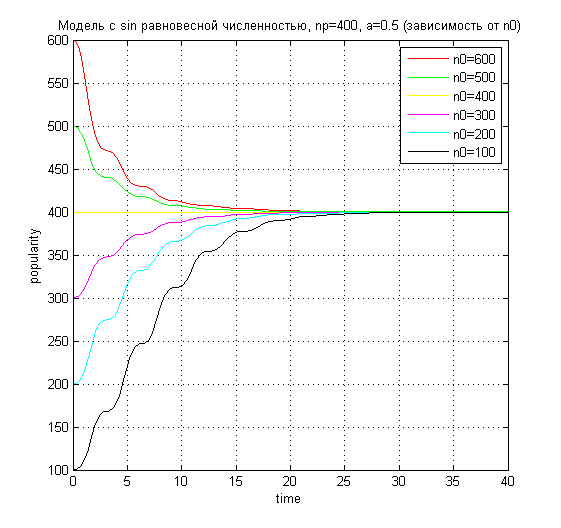

5.2.Зависимость с погрешностью

Вносим случайную погрешность и в коэффициент α, и в коэффициент ß: α(t)=α+randn(1);

ß(t)=(1-n/np)+randn(1)

Код Matlab

function f=func3(t,y)
global alpha betta n0 np;
f=(alpha+randn(1)).*(1-y/np+randn(1)).*y;
end

Результат Matlab

Зависимость от n0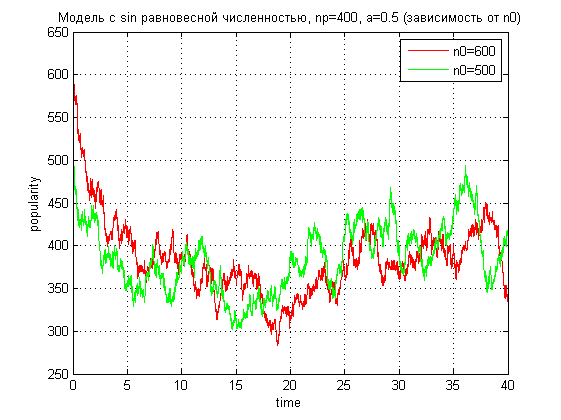

Зависимость от α

Итоги

Довольно очевидно, что смоделировать изменение популяции населения — довольно сложная задача. Все идеализированные модели довольно далеки от реальной картины постоянного изменения численности населения, даже за вычетом непредвиденных обстоятельств, резко меняющих показания. Однако модель, в которую внесён фактор случайности, приводит к довольно интересным показаниям, довольно правдиво показывая непредвиденность в численности населения.