Лабораторная работа линза. Лабораторная работа Изучение основных характеристик собирающей линзы. Цель работы
 Скачать 76.33 Kb. Скачать 76.33 Kb.
|
|
Лабораторная работа Изучение основных характеристик собирающей линзы. Цель работы:знакомство с простейшими оптическими системами, определение фокусного расстояния собирающей линзы, научиться получать различные изображения при помощи собирающей линзы. Оборудование:Собирающая линзы, источник света (свеча, лампочка), экран, линейка. Теоретические сведения: Простейшей оптической системой является линза, которая представляет собой тело, изготовленное из однородного прозрачного для света вещества и ограниченное двумя сферическими поверхностями. Если расстояние между ограничивающими линзу поверхностями в центре линзы d намного меньше радиусов их кривизны 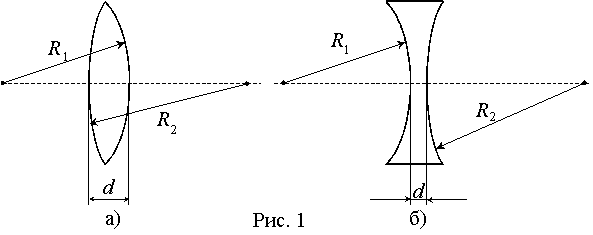 На рис. 1 изображены часто применяемые на практике двояковыпуклая (а) и двояковогнутая (б) линзы. Линия, соединяющая центрыО1и О2 ограничивающих линзу сферических поверхностей, называется главной оптической осью. Лучи, параллельные оптической оси, после прохождения через двояковыпуклую (собирающую) линзу сходятся в точке М на этой оси (рис. 2, а) (линза имеет два главных фокуса). Эта точка называетсяглавным фокусом собирающей линзы. При прохождении через двояковогнутую (рассеивающую) линзу параллельные лучи расходятся. Точка М1 на главной оптической оси, где пересекаются продолжения этих расходящихся лучей, называется главным фокусом рассеивающей линзы (рис. 2, б) (этот фокус называют также мнимым). 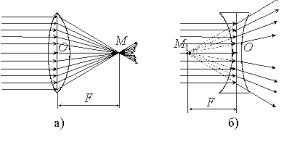 Рис. 2 Рис. 2Фокусным расстоянием линзы F называется расстояние от оптического центра линзы О до главного фокуса. Оно зависит от величины радиусов кривизны R1 и R2, ограничивающих ее сферических поверхностей и от величины показателя преломления п материала линзы. Эта зависимость имеет вид: Величина отрицательная.Одна диоптрия равна оптической силе линзы с фокусным расстоянием в один метр. Оптическая сила собирающей линзы величина положительная, а рассеивающей Основным свойством линзы является ее способность давать изображения предметов. Собирающая линза дает как действительное, так и мнимое изображение, как увеличенное, так и уменьшенное изображение, как прямое, так и обратное изображение. Это зависит от того, где расположен предмет: между линзой и фокусом, либо между фокусом и двойным фокусом, либо за двойным фокусом. Рассеивающая линза всегда дает мнимое и уменьшенное изображение. 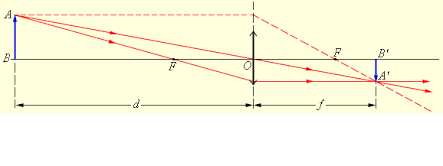 Рис. 3а Рис. 3а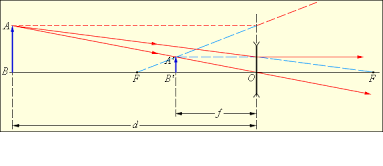 Рис.3б Рис.3бРасстояние от источника до линзы – d, расстояние от линзы до изображения - f (см. рис. 3) связаны с ее фокусным расстоянием F соотношением (формула тонкой линзы): В этой формуле знак (+) соответствует собирающей (рис. 3, а рассеивающей (рис. 3,), а знак (-) б) линзам. Если собирающая линза дает мнимое изображение, то в формуле (2) надо перед слагаемым, содержащим величину f, ставить знак (-). В 7 классе мы научились определять фокусное расстояние из свойств изображений в собирающей линзе: если источник света находится в фокусе линзы, то изображение источника отсутствует; если источник света находится в двойном фокусе линзы, то изображение становится, равным по размеру источнику света, и находится в двойном фокусе линзы по другую сторону линзы. Используя формулу (2), можно экспериментально определить фокусное расстояние Fлинзы. Этот способ состоит в следующем: определяется расстояние L между предметом и экраном, на котором получается увеличенное изображение предмета при некоторых расстояниях d и f (рис. 4, а); не трогая предмет и экран, перемещают линзу в другое положение и получают уменьшенное изображение предмета при новых расстояниях d' и f' (рис. 4, б); зная L и измерив, расстояние между двумя последовательными положениями линзы l, можно найти фокусное расстояние F линзы. 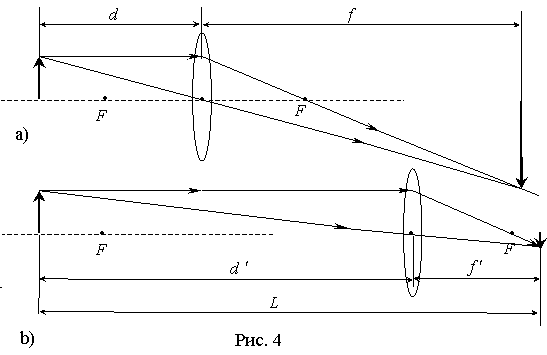 Решим поставленную задачу. Пусть (см. рис. 4) далее имеем: Представим: Поделим полученное выражение на 4Lи получим: 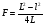 (3), (3),т.е. получили зависимость фокуса F линзы только от расстояния между источником и экраном L и расстояния между двумя последовательными положениями линзы l, которые можно померить с достаточной точностью. |
