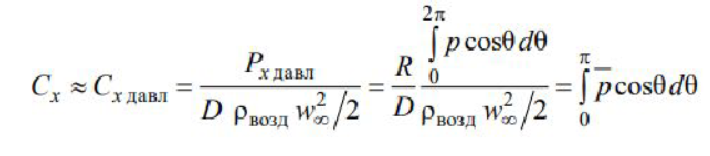Главная страница
Навигация по странице:

  • Результаты измерений

  • Результаты расчетов для 1 режима

  • Результаты расчетов для 2 режима

  • 5) Расчет коэффициента лобового сопротивления

    		•

    Лабораторная работа мжг 3 Лобовое сопротивление одиночного цилиндра при поперечном. МЖГ цилиндр. Лабораторная работа "Лобовое сопротивление одиночного цилиндра при поперечном обтекании" Студенты гр. 323140190001 Беляев Р. А, Волков П. С


    Скачать 426.65 Kb.
    НазваниеЛабораторная работа "Лобовое сопротивление одиночного цилиндра при поперечном обтекании" Студенты гр. 323140190001 Беляев Р. А, Волков П. С
    АнкорЛабораторная работа мжг 3 Лобовое сопротивление одиночного цилиндра при поперечном
    Дата07.11.2020
    Размер426.65 Kb.
    Формат файлаdocx
    Имя файлаМЖГ цилиндр.docx
    ТипЛабораторная работа
    #148672

    САНКТ-ПЕТЕРБУРГСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

    ПЕТРА ВЕЛИКОГО

    Институт Энергетики

    Высшая школа атомной и тепловой энергетики

    Лабораторная работа

    "Лобовое сопротивление одиночного цилиндра при поперечном обтекании"

    Студенты гр. 3231401/90001 Беляев Р.А,

    Волков П.С

    Григорьев А.М

    Преподаватель Кортиков Н.Н.


    Санкт-Петербург

    2020


    1. Введение



    Цель работы: экспериментальное определение лобового сопротивления цилиндра в зависимости от числа Рейнольдса.

    Объект исследования: круглый цилиндр.

    Метод исследования: экспериментальный.

    2. Описание установки



    Для проведения эксперимента используется установка, схема которой представлена на рисунке 1. Установка выполнена в виде аэродинамической трубы 1, на выходе из которой установлен вентилятор 6. Вентилятор создает разрежение в трубе, в результате чего в ней возникает движение воздуха со скоростью w∞ в направлении, указанном стрелками на рисунке 1. Значения скорости воздуха w∞ устанавливаются с помощью регулятора 5. Поскольку воздух в аэродинамическую трубу поступает из помещения лаборатории, где он практически неподвижен, для аэродинамической трубы данного типа давление торможения p* оказывается равным барометрическому давлению рб. Поперек установлен цилиндр 2 с известной высотой и длиной. Для измерения давления p на боковой поверхности цилиндра выполнено радиальное отверстие диаметром 0,5 мм, соединенное с микроманометром 4. К торцу цилиндра прикреплен диск 3 с лимбом для отсчета угла поворота цилиндра. Поворачивая цилиндр вместе с отверстием, можно измерить зависимость давления p от азимутального угла. Для измерения малых давлений в работе применен микроманометр с наклонной трубкой, схематично изображенный на рисунке 2. Наклон трубки относительно вертикали увеличивает измеряемую длину столба жидкости и, следовательно, повышает чувствительность прибора.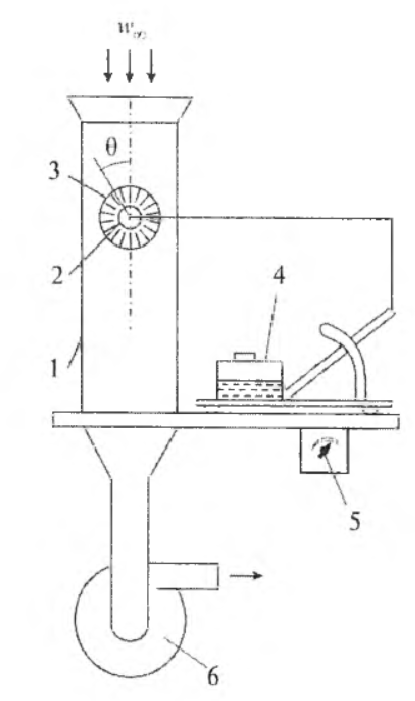



    Рис.1. Схема лабораторной установки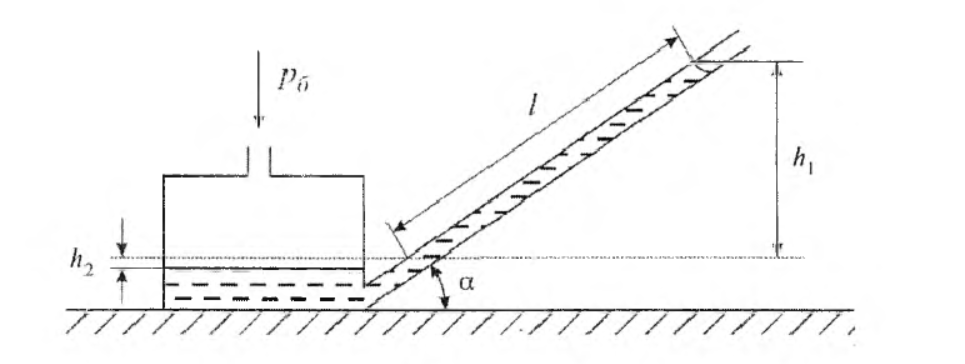



    Рис.2. Схема микроманометра с наклонной трубкой

    3. Результаты эксперимента


    Pбар = 759 мм рт. ст. = 101192 Па

    t = 22 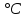=295К

    Таблица 1
    Результаты измерений

    Номер режима
    Угол θ, град

    0
    10
    20
    30
    40
    50
    60
    70
    80
    90
    100
    110
    120
    130
    140
    150
    160
    170
    180

    Показания микроманометра li, мм сп. ст.

    1
    2
    3
    5
    9
    14
    21
    24
    28
    29
    28
    27
    27
    28
    28
    29
    30
    30
    30
    30

    2
    7
    8
    11
    17
    25
    34
    46
    51
    51
    48
    47
    46
    47
    47
    47
    48
    49
    50
    41

    3
    15
    16
    21
    27
    36
    49
    56
    65
    67
    62
    61
    62
    63
    63
    64
    64
    65
    65
    65






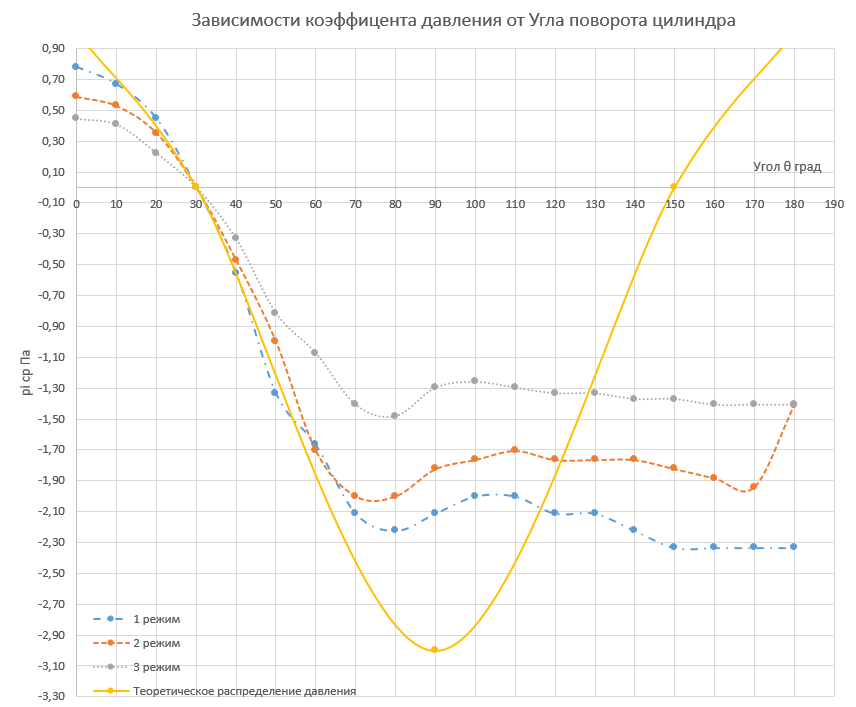
    4. Обработка результатов


    1) Расчет плотности воздуха по уравнению состояния идеального газа: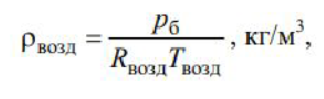



    2) Расчет скорости набегающего на цилиндр потока: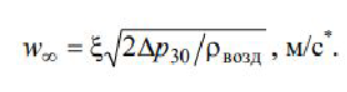



    3) Расчет числа Рейнольдса:



    4) Расчет коэффициента давления в зависимости от азимутального угла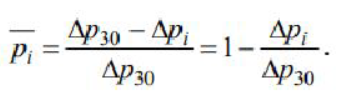


    Результаты всех расчетов по вышеуказанным формулам представлены в таблицах 2, 3 , 4, 5.

    Таблица 2


    Θ, град
    0
    10
    20
    30
    40
    50
    60
    70
    80
    90
    100
    110
    120
    130
    140
    150
    160
    170
    180

    li, мм.сп.ст.
    2
    3
    5
    9
    14
    21
    24
    28
    29
    28
    27
    27
    28
    28
    29
    30
    30
    30
    30

    Δpi, Па
    2,0
    2,9
    4,9
    8,8
    13,7
    20,6
    23,5
    27,5
    28,4
    27,5
    26,5
    26,5
    27,5
    27,5
    28,4
    29,4
    29,4
    29,4
    29,4

    p̅i
    0,8
    0,7
    0,4
    0,0
    -0,6
    -1,3
    -1,7
    -2,1
    -2,2
    -2,1
    -2,0
    -2,0
    -2,1
    -2,1
    -2,2
    -2,3
    -2,3
    -2,3
    -2,3

    p̅I *

    cos Θ
    0,8
    -0,6
    0,2
    0,0
    0,4
    -1,3
    1,6
    -1,3
    0,2
    0,9
    -1,7
    2,0
    -1,7
    0,8
    0,4
    -1,6
    2,3
    -2,2
    1,4
    Результаты расчетов для 1 режима


    Θ, град
    0
    10
    20
    30
    40
    50
    60
    70
    80
    90
    100
    110
    120
    130
    140
    150
    160
    170
    180

    li, мм.сп.ст.
    7
    8
    11
    17
    25
    34
    46
    51
    51
    48
    47
    46
    47
    47
    47
    48
    49
    50
    41

    Δpi, Па
    6,9
    7,8
    10,8
    16,7
    24,5
    33,4
    45,1
    50,0
    50,0
    47,1
    46,1
    45,1
    46,1
    46,1
    46,1
    47,1
    48,1
    49,1
    40,2

    p̅i
    0,6
    0,5
    0,4
    0,0
    -0,5
    -1,0
    -1,7
    -2,0
    -2,0
    -1,8
    -1,8
    -1,7
    -1,8
    -1,8
    -1,8
    -1,8
    -1,9
    -1,9
    -1,4

    p̅I *

    cos Θ
    0,6
    -0,4
    0,1
    0,0
    0,3
    -1,0
    1,6
    -1,3
    0,2
    0,8
    -1,5
    1,7
    -1,4
    0,6
    0,3
    -1,3
    1,8
    -1,8
    0,8
    Результаты расчетов для 2 режима Таблица 3

    Таблица 4

    Результаты расчетов для 2 режима

    Θ, град
    0
    10
    20
    30
    40
    50
    60
    70
    80
    90
    100
    110
    120
    130
    140
    150
    160
    170
    180

    li, мм.сп.ст.
    7
    8
    11
    17
    25
    34
    46
    51
    51
    48
    47
    46
    47
    47
    47
    48
    49
    50
    41

    Δpi, Па
    6,9
    7,8
    10,8
    16,7
    24,5
    33,4
    45,1
    50,0
    50,0
    47,1
    46,1
    45,1
    46,1
    46,1
    46,1
    47,1
    48,1
    49,1
    40,2

    p̅i
    0,6
    0,5
    0,4
    0,0
    -0,5
    -1,0
    -1,7
    -2,0
    -2,0
    -1,8
    -1,8
    -1,7
    -1,8
    -1,8
    -1,8
    -1,8
    -1,9
    -1,9
    -1,4

    p̅I *

    cos Θ
    0,6
    -0,4
    0,1
    0,0
    0,3
    -1,0
    1,6
    -1,3
    0,2
    0,8
    -1,5
    1,7
    -1,4
    0,6
    0,3
    -1,3
    1,8
    -1,8
    0,8
    График соответствующий данным в таблица 2, 3, 4.


    Рисунок 4 - Сравнение экспериментальных режимов с теоретической зависимостью.
    5) Расчет коэффициента лобового сопротивления




    5 Выводы


    В данной лабораторной рабы были найдены коэффициенты трения воздуха при различных скоростях потока. Построена зависимость коэффициента трения от логарифма числа Рейнольдса. Построена эпюра скорости, на ней видно, что скорость падает при приближении к стенке. Коэффициент трения, полученный

    при первом режиме, наиболее соответствует экспериментальным данным. Отклонение экспериментальных значений коэффициента трения от кривой связано с погрешностью опыта из-за не совершенности установки.

    написать администратору сайта