|
|
Проверка основного закона вращения твёрдого тела на крестообразном маятнике. Проверка основного закона вращения твёрдого тела на крестообразн. Лабораторная работа м09 Проверка основного закона вращения твёрдого тела на крестообразном маятнике Отчёт о работе Работу|
Лабораторная работаМ–09
Проверка основного закона вращения твёрдого тела на крестообразном маятнике
Отчёт о работе
Работу выполнил:
|
фамилия
|
Фецер
|
имя
|
Рашид
|
отчество
|
Каримович
|
группа
|
Д-8В31,28.1
|
Краткое теоретическое содержание работы
Основное уравнение динамики вращательного движения твердого тела:
|
М=Iε или ε=M/I
|
где
|
M —
|
Момент силы
|
I —
|
Момент инерции тела относительно оси вращения
|
ε —
|
Угловое ускорение
|
Момент силы – это ...
|
векторная физическая величина, равная векторному произведению радиус-вектора (проведённого от оси вращения к точке приложения силы — по определению), на вектор этой силы.
|
Момент инерции
|
тела относительно оси вращения равен сумме моментов инерции материальных точек, из которых состоит это тело.
|
Угловое ускорение
|
Твёрдого тела относительно неподвижной оси вращения прямо пропорционально суммарному вращающему моменту сил и обратно пропорционально моменту инерции твёрдого тела относительно оси вращения.
|
Теорема Гюйгенса-Штейнера
|
Момент инерции тела I относительно произвольной оси равен сумме момента инерции этого тела IС относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями
 . .
|
Схема установки
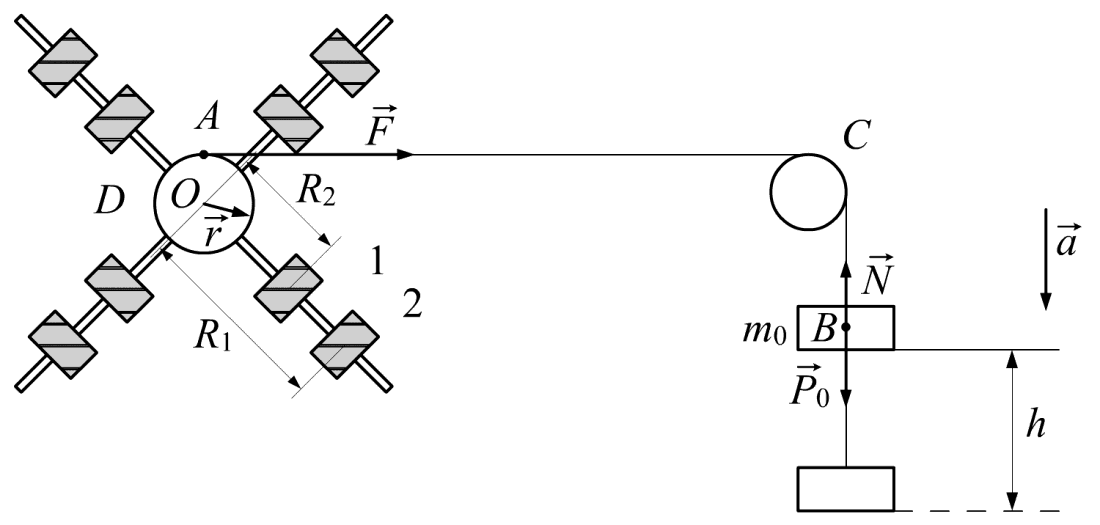
|
Обозначения
|
A —
|
Точка приложенная к валику
|
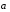 — —
|
Ускорение падающего груза
|
r —
|
Радиус валика
|
C —
|
Общая ось с маховиком
|
h —
|
Высота падения груза
|
R1 —
|
Первое расстояние груза от оси вращения маятника
|
R2 —
|
Второе расстояние груза от оси вращения маятника
|
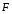 — —
|
Сила натяжения нити
|
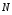 — —
|
Реакция нити приложенная к грузу
|
m0 —
|
Масса груза
|
P0 —
|
Проекция на направление движения груза по второму закону Ньютона
|
Расчетные формулы
(с пояснением величин, в них входящих)
I. Проверка соотношения
ε1 : ε2 = M1 : M2 (при I0 = const).
Момент силы
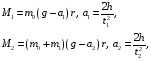
где
|
m0 —
|
Масса груза № 0
|
m1 —
|
Масса груза № 1
|
r —
|
Радиус валика
|
h —
|
Высота падения груза
|
t1 —
|
Время падения груза m0
|
t2 —
|
Время падения груза m0 +m1
|
Угловое ускорение
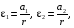
где
|
a1 —
|
Линейное ускорение падающего груза m0
|
a2 —
|
Линейное ускорение падающего груза m0 +m1
|
r —
|
Радиус валика
|
II. Проверка соотношения
ε'1 : ε'2 = I2 : I1 (при M = const).
Момент инерции
I1 = I0 + I'1, I2 = I0 + I'2,
|
I'1 =
|
Момент инерции на расстоянии R1
|
I'2 =
|
Момент инерции на расстоянии R2
|
где  — определяется по результатам таблицы 1. — определяется по результатам таблицы 1.

где
|
a'1 —
|
Линейное ускорение четырёх падающих грузов при первом времени
|
a'2 —
|
Линейное ускорение четырёх падающих грузов при втором времени
|
t1 —
|
Время первого падения грузов
|
t2 —
|
Время второго падения грузов
|
Результаты измерений
h =
|
0.75
|
m0 =
|
0.49
|
m1 =
|
0.97
|
4m =
|
0.5
|
R1 =
|
0.22
|
R2 =
|
0.11
|
Таблица 1
№
|
t1 (с)
|
t2 (с)
|
h (м)
|
m0 (кг)
|
m1 (кг)
|
d (м)
|
r (м)
|
a1 (м/с2)
(ср.)
|
a2 (м/с2)
(ср.)
|
1
|
7.4
|
4.4
|
0.75
|
0.49
|
0.97
|
0.26
|
0.13
|
0.02
|
0.07
|
2
|
7.8
|
4.6
|
3
|
7.6
|
4.8
|
ср. знач.
|
7.6
|
4.6
|
Таблица 2
№
|
t1 (с)
|
t2 (с)
|
h (м)
|
a'1 (м/с2)
(ср.)
|
a'2 (м/с2)
(ср.)
|
ε'1 (с–2)
(ср.)
|
ε'2 (с–2)
(ср.)
|
4m (кг)
|
R1 (м)
|
R2 (м)
|
1
|
16.6
|
12.2
|
0.75
|
0.005
|
0.028
|
0.38
|
0.07
|
0.5
|
0.22
|
0.11
|
2
|
16.4
|
12.6
|
3
|
16.6
|
12.4
|
ср. знач.
|
16.6
|
12.4
|
Обработка результатов измерений
I. Проверка соотношения
ε1 : ε2 = M1 : M2.
Подставим полученные экспериментальные результаты в расчётные формулы
и произведем вычисления
б) Моменты сил
|
M1 = m0 (g – a1)r =
|
0.49(9.8-0.03)0.13=0.62
|
M2 = (m0 + m1) (g – a2)r =
|
(0.49+0.97)(9.8-0.08)0.13=1.84
|
Проверим отношения (при I0=
|
I
|
):
|
ε1 : ε2 =
|
0.23:0.61=0.38
|
M1 : M2 =
|
0.62:1.84=0.34
|
Вывод
Проведя эксперимент, мы рассмотрели сложное движение тел, сочетающего вращательное движение с поступательным и рассчитали моменты силы маятника двумя способами: экспериментально и теоретически.
|
II. Проверка соотношения
ε'1 : ε'2 = I2 : I1.
a) Среднее значение угловых ускорений
|
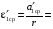
|
0.005/0.13=0.04
|

|
0.028/0.13=0.21
|
б) Моменты инерции
|
Из таблицы 1 определим 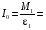
|
0.62/0.23=2.7
|
I'1 =
|
4m =0.5* =0.5*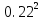 =0.5*0.0484=0.0242 кг* =0.5*0.0484=0.0242 кг*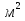
|
I'2 =
|
4m =0.5* =0.5* =0.5*0.0121=0.0605 кг* =0.5*0.0121=0.0605 кг*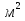
|
Найдем
|
I1 = I0 + I'1 =
|
2.7+0.0242=2.7242
|
I2 = I0 + I'2 =
|
2.7+0.0605=2.7605
|
Проверим отношения (при M =
|
Iε
|
):
|
ε'1 : ε'2 =
|
0.38:0.08=4.75
|
I2 : I1 =
|
2.7605:2.7242=1.01
|
Вывод
Проведя эксперимент, мы рассмотрели сложное движение тел, сочетающего вращательное движение с поступательным и рассчитали моменты инерции маятника двумя способами: экспериментально и теоретически.
| |
|
|
 Скачать 77.21 Kb.
Скачать 77.21 Kb.

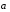 —
—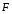 —
—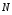 —
—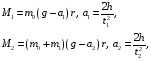
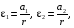
 — определяется по результатам таблицы 1.
— определяется по результатам таблицы 1.


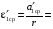

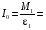
 =0.5*
=0.5*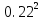 =0.5*0.0484=0.0242 кг*
=0.5*0.0484=0.0242 кг*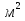
 =0.5*
=0.5* =0.5*0.0121=0.0605 кг*
=0.5*0.0121=0.0605 кг*