заочники_Л.Р.М-5к. Лабораторная работа м 5к изучение законов сохранения в механике поступательного движения цель работы
 Скачать 1.78 Mb. Скачать 1.78 Mb.
|
|
Тихомиров Ю.В., Степанова В.А. Лабораторная работа М – 5к ИЗУЧЕНИЕ ЗАКОНОВ СОХРАНЕНИЯ В МЕХАНИКЕ ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ 1. Цель работы Исследование законов сохранения импульса и энергии при упругом и неупругом соударении двух тел; экспериментальное определение зависимости тепловыделения при неупругом столкновении от соотношения масс. 2. Подготовка к работе Изучите теоретический материал по теме «Законы сохранения в механике» по материалу лекций и учебников [1, 2]. Ознакомьтесь с компьютерной моделью и методикой проведения виртуального эксперимента в разделе 4 данного описания. Подготовьте ответы на вопросы из раздела 7. Оформите проект отчета по лабораторной работе. 3. Краткая теория Закон сохранения механической энергии и закон сохранения импульса позволяют находить решения механических задач в тех случаях, когда действующие силы неизвестны. Примером такого рода задач является ударное взаимодействие тел. Механическая система тел, на которую не действуют внешние силы, называется замкнутой (или изолированной). В реальном мире такой системы не может быть, так как нет возможности убрать всякое внешнее взаимодействие. Замкнутая система тел – это физическая модель системы тел, которые якобы взаимодействуют только друг с другом, внешние силы не берутся во внимание, ими пренебрегают. В механической системе, состоящей из нескольких тел, согласно третьему закону Ньютона, силы, действующие между этими телами, равны и противоположно направлены, то есть векторная сумма внутренних сил равна нулю. В случае замкнутой системы тел справедлив закон сохранения импульса: полный (суммарный) импульс замкнутой системы тел сохраняется, то есть не изменяется с течением времени, при любых процессах, происходящих в этой системе
где υi – скорость i -той материальной точки массойmi. Для замкнутой системы двух тел закон сохранения импульса в общем виде запишется так
где 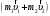 и и 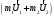 – импульс системы тел в разные моменты времени (до и после взаимодействия тел, соответственно). – импульс системы тел в разные моменты времени (до и после взаимодействия тел, соответственно).Энергия - это универсальная мера различных форм движения и взаимодействия. С различными формами движения связывают различные формы энергии: механическую, тепловую, электромагнитную, ядерную и др. В одних явлениях форма движения материи не изменяется (например, горячее тело нагревает холодное), в других - переходит в иную форму (в результате трения механическое движение превращается в тепловое). Очень важно, что во всех случаях энергия, отданная (в той или иной форме) одним телом другому телу, равна энергии, полученной последним телом. Кинетическая энергия Ек– это энергия механического движения тела или системы тел. Тело, масса которого равна m, движущееся со скоростью υ, обладает кинетической энергией
Кинетическая энергия механической системы тел равна сумме кинетических энергий тел, входящих в систему
где υi – скорость i -той материальной точки массойmi. Закон сохранения механической энергии можно сформулировать так: в замкнутой системе тел суммарная энергия остается величиной постоянной при любом взаимодействии тел между собой; энергия может переходить из одного вида в другой. Соударение (удар, столкновение) — это модель взаимодействия двух тел, длительность которого равна нулю (мгновенное событие). Такая модель применяется для описания реальных событий, длительностью которых можно пренебречь в условиях данной задачи. При соприкосновении тела обмениваются энергией и импульсом. После соударения они двигаются со скоростями, которые отличаются по направлению и величине от их скоростей до столкновения. Силы взаимодействия между сталкивающимися телами (ударные или мгновенные силы) столь велики, что внешними силами, действующими на них, можно пренебречь. Это позволяет систему тел в процессе их соударения приближенно рассматривать как замкнутую систему и применять к ней законы сохранения. Различают два типа удара: абсолютно упругий и абсолютно неупругий. Абсолютно упругий удар — столкновение тел, в результате которого в обоих взаимодействующих телах не остается никаких деформаций и вся кинетическая энергия, которой обладали тела до удара, после удара снова превращается в кинетическую энергию (подчеркнем, что это идеализированный случай, когда в обоих взаимодействующих телах не остается никаких деформаций и они не нагреваются). При таком ударе (рис.1) кинетическая энергия вначале переходит в потенциальную энергия упругой деформации. Затем тела возвращаются к первоначальной форме, отталкивая друг друга. Потенциальная энергия упругой деформации переходит в кинетическую энергию. После удара тела разлетаются.  Рис.1. Схема столкновения при абсолютно упругом ударе. Для абсолютно упругого удара выполняются закон сохранения импульса и закон сохранения кинетической энергии. Обозначим массы тел m1 и m2, их скорости до удара U10 и U20, а после удара U1 и U2. Согласно закону сохранения импульса и тому, что суммарная кинетическая энергия шаров до Ек0 и Е0 после удара одинакова, можем записать равенства
Равенства (5) и (6) запишем в виде:
Из равенств (7) и (8) следует, что:
Умножив (9) на т2и вычтя результат из (7), а затем умножив (9) на т1и сложив результат с (7), получим скорости шаров после удара:
Для численных расчетов необходимо спроецировать соотношения (10) на ось Х (рис. 1). Абсолютно неупругий удар – это столкновение двух тел, в результате которого тела объединяются, двигаясь дальше как единое целое. При таком ударе (рис.2) происходит неупругая деформация тел и их слипание. Кинетическая энергия тел полностью или частично превращается во внутреннюю энергию; после удара столкнувшиеся тела либо движутся с одинаковой скоростью, либо покоятся. Для абсолютно неупругого удара выполняется закон сохранения импульса и не выполняется закон сохранения кинетической энергии, т.к. часть её переходит во внутреннюю энергию тел. Абсолютно неупругий удар — пример того, как происходит «потеря» механической энергии под действием диссипативных сил. 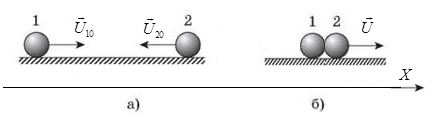 Рис.2. Схема столкновения при неупругом ударе. Рассмотрим неупругое столкновение двух шаров массами т1и m2,скорости которых до удара U10 и U20.После удара шары, объединившись, двигаются со скоростью U. Согласно закону сохранения импульса:
откуда
Для практических расчетов нужно спроецировать равенство (12) на выбранную ось Х (рис. 2). Кинетические энергии шаров до удара (Ек0) и после удара (Екʹ), соответственно, равны
Потеря кинетической энергии ∆Ек равна работе сил деформации в процессе удара и переходит во внутреннюю энергию взаимодействия (в частности, в тепловую энергию Q)
которая вычисляется по формуле
4. Методика виртуального эксперимента В данной лабораторной работе используется компьютерная модель, основанная на законах сохранения импульса и энергии при соударениях двух тел (тележек). Откройте компьютерную модель «Упругие и неупругие соударения». Внимательно рассмотрите модель, найдите все регуляторы и другие основные элементы. Компьютерная модель «Упругие и неупругие соударения» позволяет устанавливать значения массы тележек m1 и m2 и их скорости U10 и U20 до соударения регуляторами соответствующих величин, расположенными слева внизу диалогового окна модели и обозначенными как «Параметры системы» (рис.3). В модели есть кнопка управления, которой задают режимы модели. Щелкнув мышью по кнопке «Сброс» (нижняя часть кнопки управления), задают параметры величин для виртуального эксперимента. Запускают виртуальный эксперимент кнопкой «Пуск» (средняя часть кнопки управления). Кнопкой «Назад» (левая часть кнопки управления) возвращаются к ранее заданным параметрам величин виртуального эксперимента; в этом режиме также возможно задавать исходные параметры величин.  Рис.3. Диалоговое окно компьютерной модели «Упругие и неупругие соударения» в режиме «Сброс» (отдельно показаны обозначения кнопок управления режимов). В отдельном блоке модели фиксируются значения параметров системы (скорости, импульса и энергии тележек) в любой момент времени. Указываемые значения скорости, импульса и энергии тележек после удара иногда имеют вычислительные ошибки, обусловленные при моделировании математическими расчетами. Например, указанные значения импульсов тележек после их упругого столкновения на рис.4 не верны, так как  и и 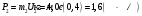 , ,а модель показывает 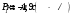 и и 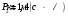 . . Рис.4. Диалоговое окно компьютерной модели «Упругие и неупругие соударения» в режиме «Пуск» В нашем виртуальном эксперименте тележка массой т1 (величина которой не меняется в данных измерениях) движется равномерно прямолинейно со скоростью U10 и сталкивается со второй тележкой, движущейся навстречу соскоростью U20 = – U10. Необходимо провести серию измерений скоростей тележек после столкновений при разных значениях массы второй тележки m2, величину которой равномерно увеличивают, начиная со значения m2 = т1. При указанных условиях эксперимента, проекция соотношений (10) на ось Х (рис. 1) дает формулы численных расчетов скоростей тележек после упругого столкновения
а проекция равенства (12) на ось Х (рис. 2) дает формулу вычисления скорости тележек после неупругого столкновения
5. Порядок выполнения работы Эксперимент 1. Исследование абсолютно упругого удара. 1. Запустите виртуальный эксперимент «Упругие и неупругие соударения». 2. В режиме «Сброс» установите метку "Абсолютно упругое" в «Тип столкновения». 3. Установите значение массы первой тележки m1 и ее начальную скорость U10, указанные в табл. 1 для вашего варианта (для определения номера варианта см. *ссылку в конце текста лабораторной работы). Массу второй тележки установите равной массе m1, а её начальную скорость установите равной U20 = – U10. 4. Нажмите мышью на кнопку «Пуск» на экране монитора. Запишите в табл. 2 результаты измерений величин скоростей тележек U1 и U2 (в столбец «модель») после столкновения (эти значения фиксируются в блоке модели «Скорости, импульсы и энергии» в момент времени остановки виртуального эксперимента). 5. Нажмите кнопку «Назад». Увеличив на 1 кг значение массы второй тележки, повторите измерения согласно п.4. 6. Увеличивая на 1 кг массу второй тележки, повторите измерения (п.4 и п.5) ещё три раза. Таблица 1. Значения исходных характеристик для экспериментов (не перерисовывать).
Таблица 2. Результаты измерений и расчетов для абсолютно упругого удара.
Эксперимент 2. Исследование абсолютно неупругого удара. 1. Запустите виртуальный эксперимент «Упругие и неупругие соударения». 2. В режиме «Сброс» установите метку "Абсолютно неупругое" в «Тип столкновения». 3. Установите значение массы первой тележки m1 и ее начальную скорость U10, указанные в табл. 1 для вашего варианта. Массу второй тележки установите равной массе m1, а величину её начальной скорости установите равной U20 = – U10. 4. Нажмите мышью на кнопку «Пуск» на экране монитора. Запишите в табл. 3 результаты измерений величин скоростей тележек U1 = U2 = U(в столбец «модель») после столкновения (эти значения фиксируются в блоке модели «Скорости, импульсы и энергии» в момент времени остановки виртуального эксперимента). 5. Нажмите кнопку «Назад». Увеличив на 1 кг значение массы второй тележки, повторите измерения согласно п.4. 6. Увеличивая на 1 кг массу второй тележки, повторите измерения (п.4 и п.5) ещё три раза. Таблица 3. Результаты измерений и расчетов для абсолютно неупругого удара.
6. Обработка результатов измерений Эксперимент 1. 1. Вычислите суммарный импульс тележек до столкновения по формуле 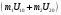 , после столкновения по формуле , после столкновения по формуле 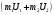 и запишите результаты в табл. 2 для пяти измерений. и запишите результаты в табл. 2 для пяти измерений.2. Для каждого измерения сравните значения импульсов до и после столкновения. В случае не совпадения чисел, вычислите для таких измерений величины скоростей тележек U1 и U2 после столкновения по формуле (17) с точностью до второго знака после запятой и запишите результаты в столбец «вычисление». Вычисленные значения скоростей будут истинными. 3. Вычислите суммарную кинетическую энергию тележек до (Ек0) удара и после (Ек) удара с учетом истинных значений скоростей для всех измерений и запишите в табл. 2. 4. Проанализируйте полученные результат и запишите вывод. Эксперимент 2. 1. Вычислите суммарный импульс тележек до столкновения по формуле 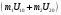 , после столкновения по формуле , после столкновения по формуле 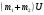 и запишите результаты в табл. 3 для пяти измерений. и запишите результаты в табл. 3 для пяти измерений.2. Для каждого измерения сравните значения импульсов до и после столкновения. В случае не совпадения чисел, вычислите для таких измерений величину скорости тележек U после столкновения по формуле (18) с точностью до второго знака после запятой и запишите результаты в столбец «вычисление». Вычисленные значения скоростей будут истинными. 3. Вычислите тепловую энергию Q по формуле (16) с учетом истинных значений скоростей для всех измерений и запишите в табл. 3. 4. Проанализируйте полученные результаты величины тепловыделения от массы тележек и запишите вывод. 7. Вопросы для подготовки к допуску 1. Дайте определение абсолютно упругого удара и абсолютно неупругого удара. При каком ударе систему двух соударяющихся тел можно считать замкнутой? 2. Сформулируйте закон сохранения импульса, запишите его математическое выражение и поясните физический смысл величин, в него входящих. 3. Какой формулой определяется кинетическая энергия? Изменится ли кинетическая энергия тела при изменении направления вектора его скорости? 4. Почему при абсолютно неупругом ударе не выполняется закон сохранения кинетической энергии? 5. Шарик массой m1 со скоростью υ1 налетает на покоящийся шарик массой m2. Считая удар центральным и абсолютно упругим, определите скорости шаров u1 и u2 после удара. 6. Два шарика 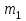 =2 кг и =2 кг и 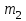 = 3 кг движутся навстречу друг другу со скоростями υ1 =8 м/с и υ2 = 4 м/с. Определите изменение энергии шаров после неупругого соударения. = 3 кг движутся навстречу друг другу со скоростями υ1 =8 м/с и υ2 = 4 м/с. Определите изменение энергии шаров после неупругого соударения. 7. На покоящийся шар налетает со скоростью υ = 2 м/с другой шар одинаковой с ним массы. В результате упругого столкновения движущийся до соударения шар изменил направление движения на угол α =300. Определите скорости шаров после удара. 8. Литература Трофимова Т.И. Курс физики. - М.: издательский центр "Академия" (или другие издательства), 2012 – 2020 г.г. Савельев И.В. Курс общей физики. Учебное пособие для втузов. В 5 кн. Кн. 1. Механика. Молекулярная физика. – Спб.: Лань (или другие издательства), 2012 – 2020 г.г. *Как определить номер варианта при выполнении лабораторной работы
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

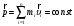 ,
,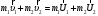 ,
,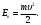
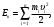
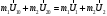 или
или 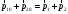
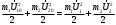
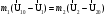
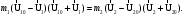
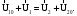
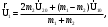

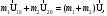
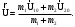
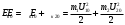 ,
,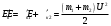 .
.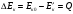 ,
,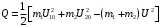 .
.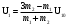 и
и 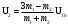 ,
,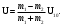
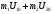 ,
,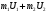 ,
,