лаб 1. Лабораторная работа Моделирование изменения денежных средств на вкладе
 Скачать 50.81 Kb.
|
|
Лабораторная работа 1. Моделирование изменения денежных средств на вкладе. 1.Общая постановка задачи на исследование. Клиент банка открывает вклад, размещая на нем денежные средства при условии начисления i сложных процентов один раз в год. Определить, как будет происходить изменение денежных средств на вкладе по истечении t лет ( 1, 2, ...t ) в двух случаях: 1. В банке при открытии вклада было размещено 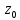 тыс. руб., пополнение счета вкладчиком в дальнейшем не производится.2. После первоначального размещения 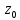тыс. руб. вкладчик ежегодно после начисления процентов вносит дополнительную сумму так, что каждый год он увеличивает дополнительно размещаемую сумму по сравнению с предыдущим годом на величину 0,1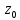 Решить задачу при следующих исходных данных: 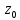=100 4p 3q1, ip+q 1 , где числа p и q задает преподаватель.Выполнить расчет изменения денежных средств на вкладе для двух рассмотренных случаев. Выяснить, через сколько лет в первом случае вклад удвоится. Определить, через сколько лет во втором случае вклад увеличится в пять раз. Изменение денежных средств проиллюстрировать таблицей. Построить графики изменения суммы вклада. В условиях второй схемы формирования денежных средств определить, какую сумму 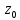необходимо разместить на вкладе, чтобы через 5 лет наращенная сумма превысила . 10(100 4p 3q1).2.Вариант студента: Номер по списку: 3 Вариант: 3, p=0; q=3 3.Задание на лабораторную работу с указанием исходных данных в соответствии с вариантом. Решить задачу при следующих исходных данных: 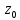=1004p3q1=123;ip+q+18; 2. Выполнить расчет и выяснить, через, сколько лет вклад удвоится без пополнения счета. 3. Рассчитать, через, сколько лет вклад увеличится в пять раз при ежегодном внесении дополнительной суммы. 4. Изменение денежных средств на вкладе для обоих случаев проиллюстрировать общей таблицей. 5. Построить графики изменения суммы вклада для обоих случаев. 6. Для задания №3, рассчитать сумму 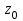 , которую необходимо разместить на вкладе, чтобы через 5 лет наращенная сумма превысила величину 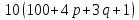 . 7. Результат расчета проиллюстрировать отдельной таблицей. Случай 1. Обозначим через 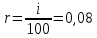 показатель, описывающий приращение вклада по сравнению с предыдущим годом за счет начисления процентовВ результате получаем: 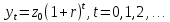 Формула задает изменение денежных средств на вкладе в случае начисления так называемых сложных процентов Случай 2. Рассмотрим теперь вторую задачу. Пусть 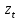 – сумма денежных средств ежегодно дополнительно размещаемых на вкладе. Согласно условию имеем: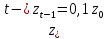 Таким образом, окончательно имеем : 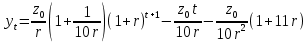 Формула описывает изменение денежных средств на вкладе по истечении t лет, 1, 2, ...t 4.Решение задачи (выполненное в соответствии с методическими рекомендациями) с подстановкой исходных данных в соответствии с вариантом. Пусть p=1; q=6, тогда исходные данные: 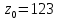 , i 8 . Показатель, описывающий приращение вклада, равен 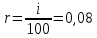. Согласно первому случаю процесс приращения вклада описывается формулой: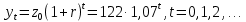 Согласно второму случаю вклад растет согласно формуле: 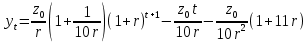Для удобства выполнения расчетов отдельно вычислим постоянные величины в формуле 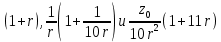 Построим расчетную область на листе Excel (рис. 1.1), где соответственно заполним ячейки. Подсчитаем величину удвоенного вклада: Е6 =2*B3. Посмотрим в столбце с данными расчета по первому случаю, когда значение 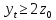 . Этому условию соответствует ячейка В17, в которой значение yt=265,55при этом t =10. Следовательно, через 10 лет вклад, рассчитываемый согласно условиям первого случая удвоится. А рассчитываемый согласно условиям второго случая увеличится в пять раз через t=3, то есть через 3 года. 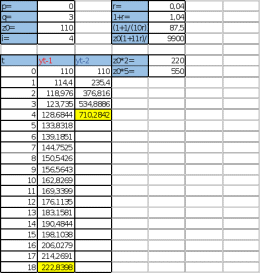 Рис. 1. Вычисление изменения вклада Построим графики отдельно для иллюстрации изменения вклада в условия первого и второго случаев. 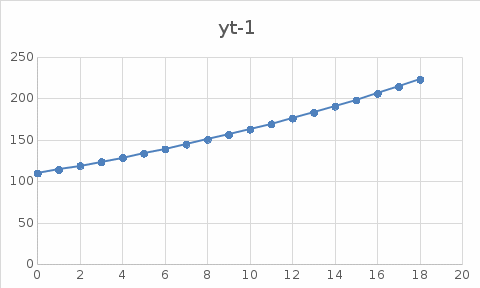 Рис. 1.2 Изменение суммы вклада в условия первого случая 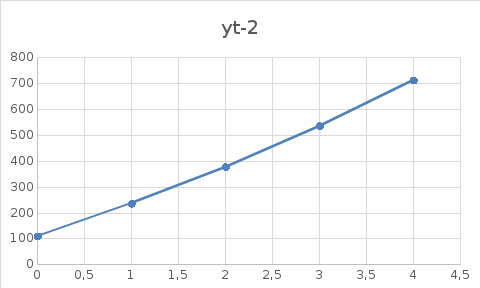 Рис 1.3 Изменение суммы вклада в условия второго случая Определим, какую сумму 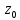необходимо разместить на вкладе в условиях второго случая, чтобы через 5 лет наращенная сумма превысила 10(1004p3q1) . 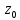Выразим при условии, что t=5, y5=1230Выполним расчет:
Рис. 1.4 Определение начальной суммы вклада Таким образом, можно сказать, что начальный вклад должен составлять не менее 136,58 тыс. руб., чтобы через пять лет сумма была не менее 1230 тыс. руб. на счете. 5. Вывод: В ходе выполнения лабораторной работы я научился определять изменения денежных средств на вкладе, составлять математические модели экономических задач в Microsoft Office Excel.
| ||||||||||||||||||||||||||||||