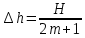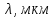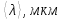Опыт Юнга.. Лабораторная работа Опыт Юнга

Название	Лабораторная работа Опыт Юнга
Дата	19.04.2023
Размер	36.5 Kb.
Формат файла
Имя файла	Опыт Юнга..docx
Тип	Лабораторная работа #1072860

Министерство науки и высшего образования Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Сибирский государственный университет геосистем и технологий»
(ФГБОУ ВО «СГУГиТ»)

Кафедра физики

ЛАБОРАТОРНАЯ РАБОТА

«Опыт Юнга»

по дисциплине: «Физика»

Студент: группа ГКз-21

Руководитель: Костюченко В.Я.

Новосибирск 2021

1.2. Компьютерная лабораторная работа «Опыт Юнга»

Цель работы:

1) изучить явление интерференции световых волн;

2) познакомится со схемой опыта Томаса Юнга;

3) определить длину волны света.

Оборудование и программное обеспечение:

1) персональный компьютер с операционной системой Windows.

2) программа «Diffraction_Young».

Ход работы

Установим флажок «Опыт Юнга», число щелей N = 2, ширину щели b = 2,5 мкм, ширину промежутка между щелями a = 7,00 мкм, при этом расстояние d будет равно 9,50 мкм. Проведем измерения и запишем в таблицу, далее дважды изменим значение a и повторим эксперимент два раза, занося данные в таблицу.

№ задачи	№ опыта	Ширина щели b = 2,5 мкм. Расстояние до экрана, L = 1,5 м
№ задачи	№ опыта	a, мкм	d, мкм	m	H, мкм				оценка	Общая оценка
I	1	7	9,5	3	0,5	0,0714	0,45	0,453	5	5
	2	7,9	10,4	4	0,58	0,064	0,444
	3	8,80	11,3	4	0,56	0,062	0,467
II	1	7	9,5	2	0,56	0,112	0,70	0,69	5
	2	7,2	9,7	2	0,54	0,108	0,69
	3	7,4	9,9	2	0,52	0,104	0,68
III	1	7	9,5	3	0,58	0,083	0,525	0,54	5
	2	7,5	10	3	0,6	0,085	0,56
	3	8,1	10,6	3	0,54	0,077	0,54

Таким образом, у каждого цвета разная длина волны.

Контрольные вопросы

1. Получите условие максимума и минимума интенсивности света при

интерференции волн от двух когерентных источников.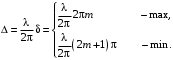

После сокращения получим условия на :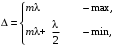

m=0, 1, 2…

2. В чем заключается явление интерференции волн?

Интерференция волн — взаимное увеличение или уменьшение результирующей амплитуды двух или нескольких когерентных волн при их наложении друг на друга. Сопровождается чередованием максимумов (пучностей) и минимумов (узлов) интенсивности в пространстве.

3. Что называется шириной интерференционной полосы?

Расстояние между двумя соседними максимумами называется расстоянием между интерференционными полосами, а расстояние между соседними минимумами – шириной интерференционной полосы.

4. Как зависит ширина интерференционной полосы от расстояния

между щелями и от длины волны?

Ширина интерференционной полосы прямо пропорциональна длине волны и расстоянию между щелями.

5. Получить расчетную формулу для определения длины волны света.

В соответствии с условием минимума имеем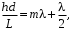

то есть для координаты m-го минимума h_m получается формула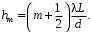

Ширина полосы равна разности координат соседних минимумов: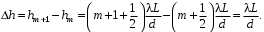

Мы видим, что в центре экрана все интерференционные полосы имеют одинаковую ширину. Измерив её, можно найти длину волны света по формуле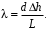

Вывод:

1) было изучено явление интерференции световых волн;

2) была рассмотрена схема опыта Томаса Юнга;

3) определена длина волны света.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Тюшев А.Н., Дикусар Л.Д. Курс лекций по физике. Ч. 3. Колебания и волны. Волновая оптика: учеб. пособие. – Новосибирск: СГГА, 2011. – С. 111, 116–122.

2. Тюшев А.Н. Физика в конспективном изложении. Ч. 2. Колебания. Волны. Волновая оптика. – Новосибирск, СГГА, 2002. – С. 63–64, 68–74.

3. Трофимова Т.И. Курс физики: учеб. пособие. – М.: Академия, 2015. – С. 331–332, 337–340.