лабораторная работа. Лабораторная работа Определение коэффициента динамической вязкости жидкости методом Стокса
 Скачать 2.41 Mb. Скачать 2.41 Mb.
|
|
Шкробит Валерия Сергеевна, вариант 69 Лабораторная работа 2.1. «Определение коэффициента динамической вязкости жидкости методом Стокса» Цель работы: изучение явления внутреннего трения в жидкостях и опытное определение величины коэффициента вязкости жидкости методом Стокса на виртуальной лабораторной установке. Теоретическая часть Различают два типа течения вязкой жидкости – ламинарное и турбулентное. Турбулентным называется такое течение жидкости, при котором её частицы совершают неустановившееся и неупорядоченные движения по сложным траекториям, приводящим к перемешиванию слоёв. Ламинарное – это упорядоченное течение жидкости, при котором траектории движения соседних частиц мало отличаются друг от друга. При ламинарном течении жидкость можно рассматривать как совокупность отдельных слоёв, движущихся с различными скоростями. Это обусловлено тем, что при движении слоев жидкости относительно друг друга с различными скоростями между ними возникает тормозящая сила, это сила внутреннего трения или сила вязкости. Вязкость – это свойство жидкости оказывать противодействие перемещению её слоёв относительно друг друга. Для перемещения пластинки необходимо приложить силу, по величине равную силе трения. Если слои жидкости находятся на расстоянии Х и движутся с различными скоростями, то верхние слои будут ускорять движение средних слоёв, а нижние – замедлять. 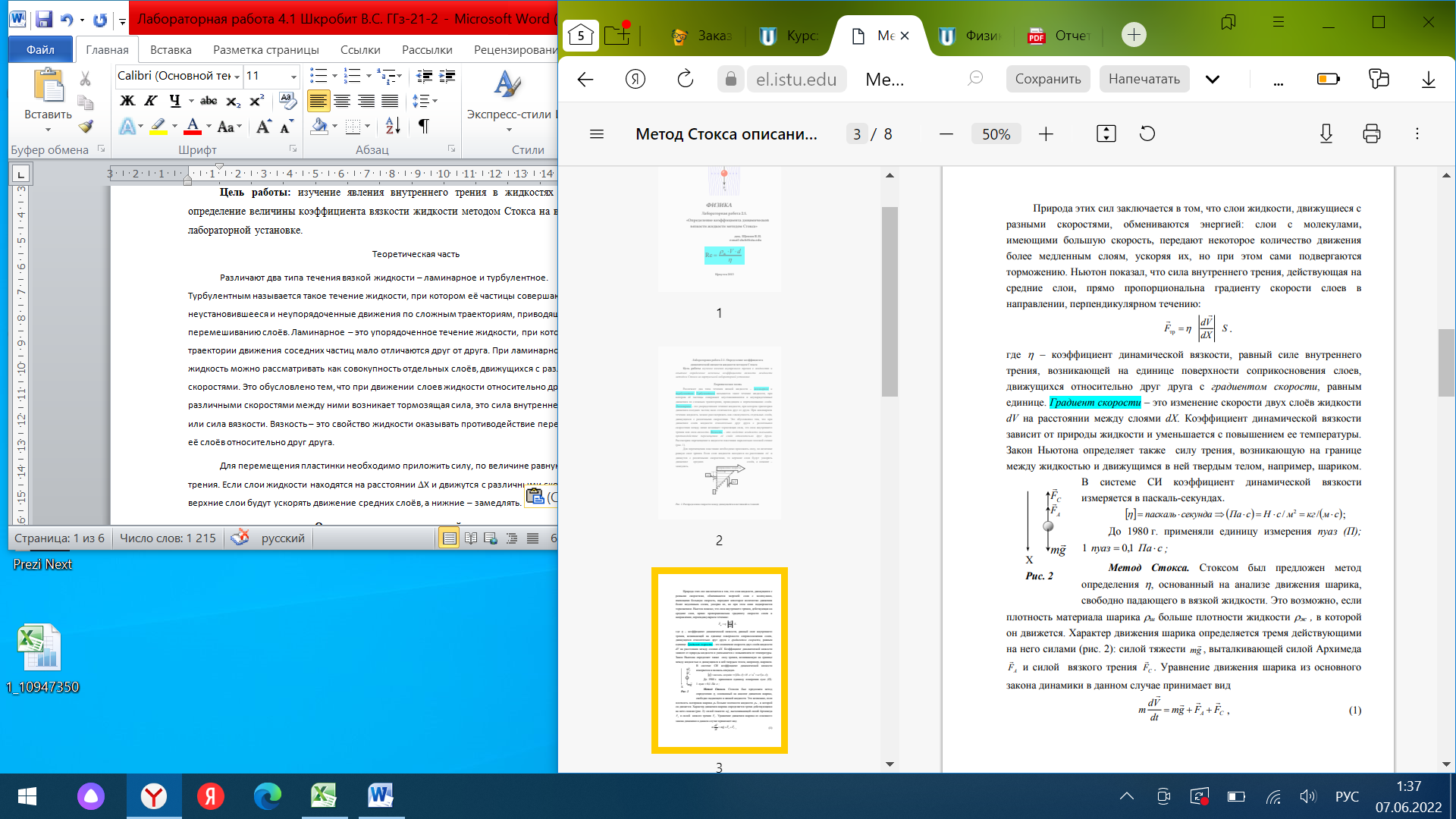 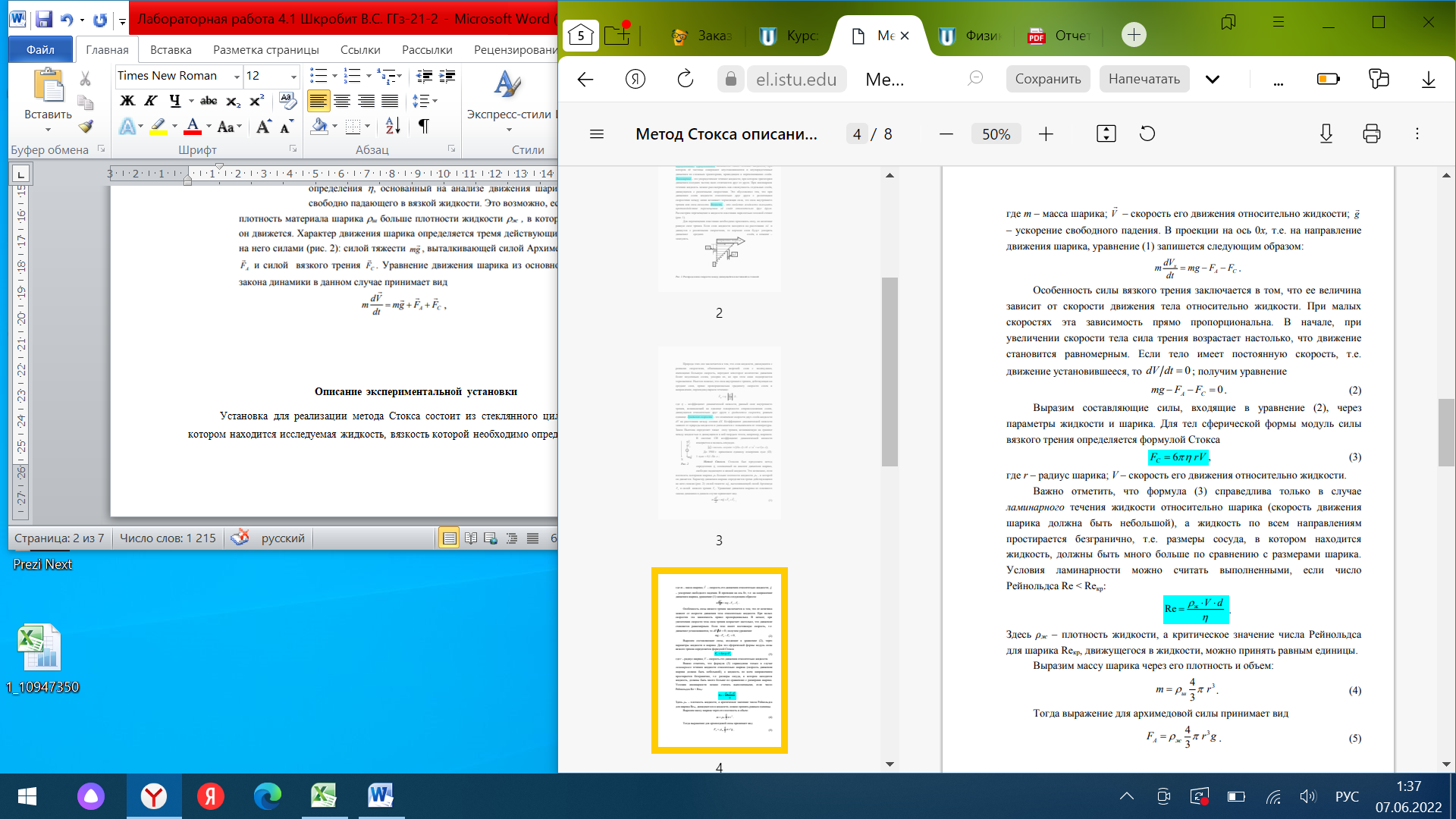 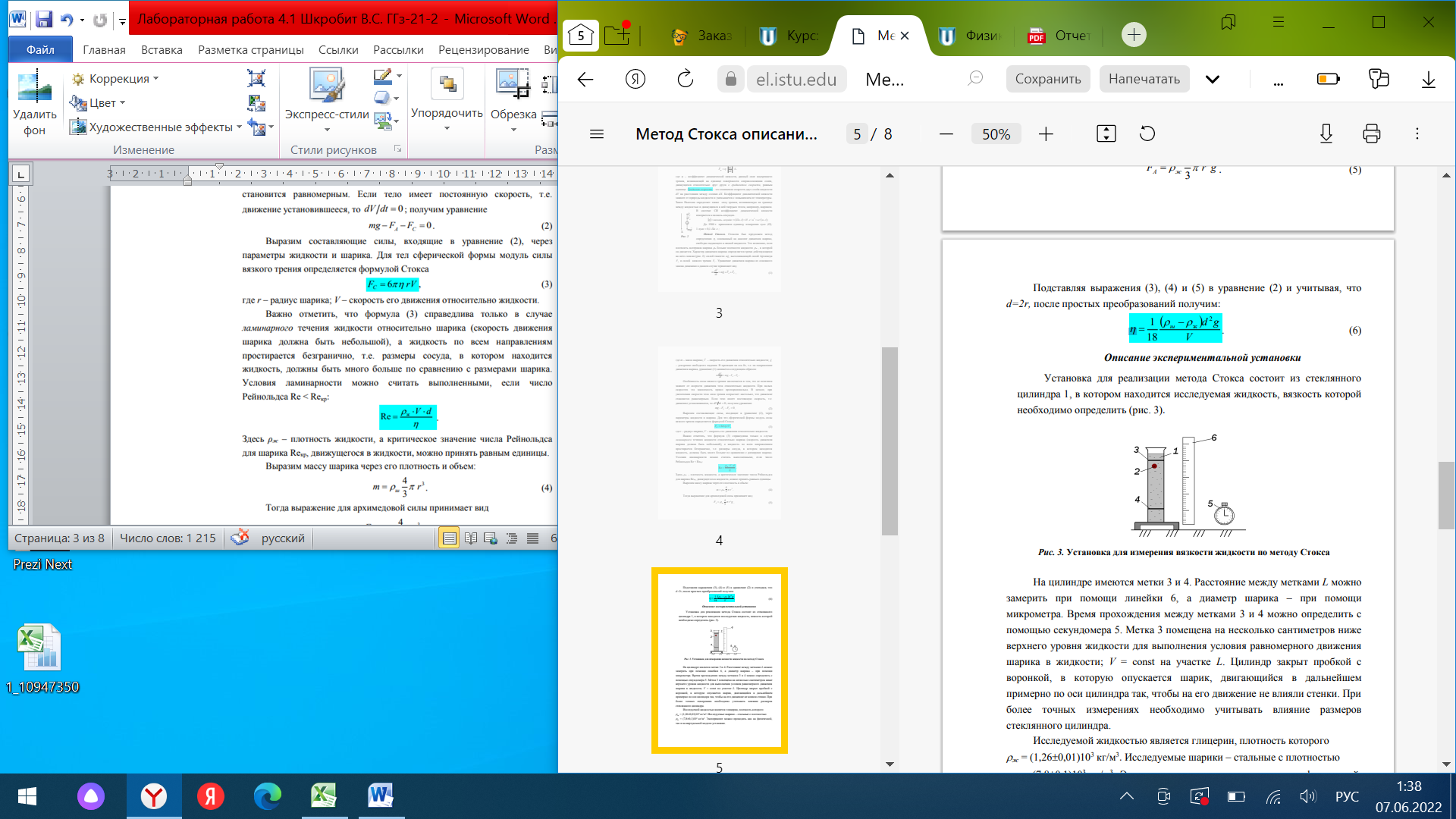 Описание экспериментальной установки Установка для реализации метода Стокса состоит из стеклянного цилиндра 1, в котором находится исследуемая жидкость, вязкость которой необходимо определить: 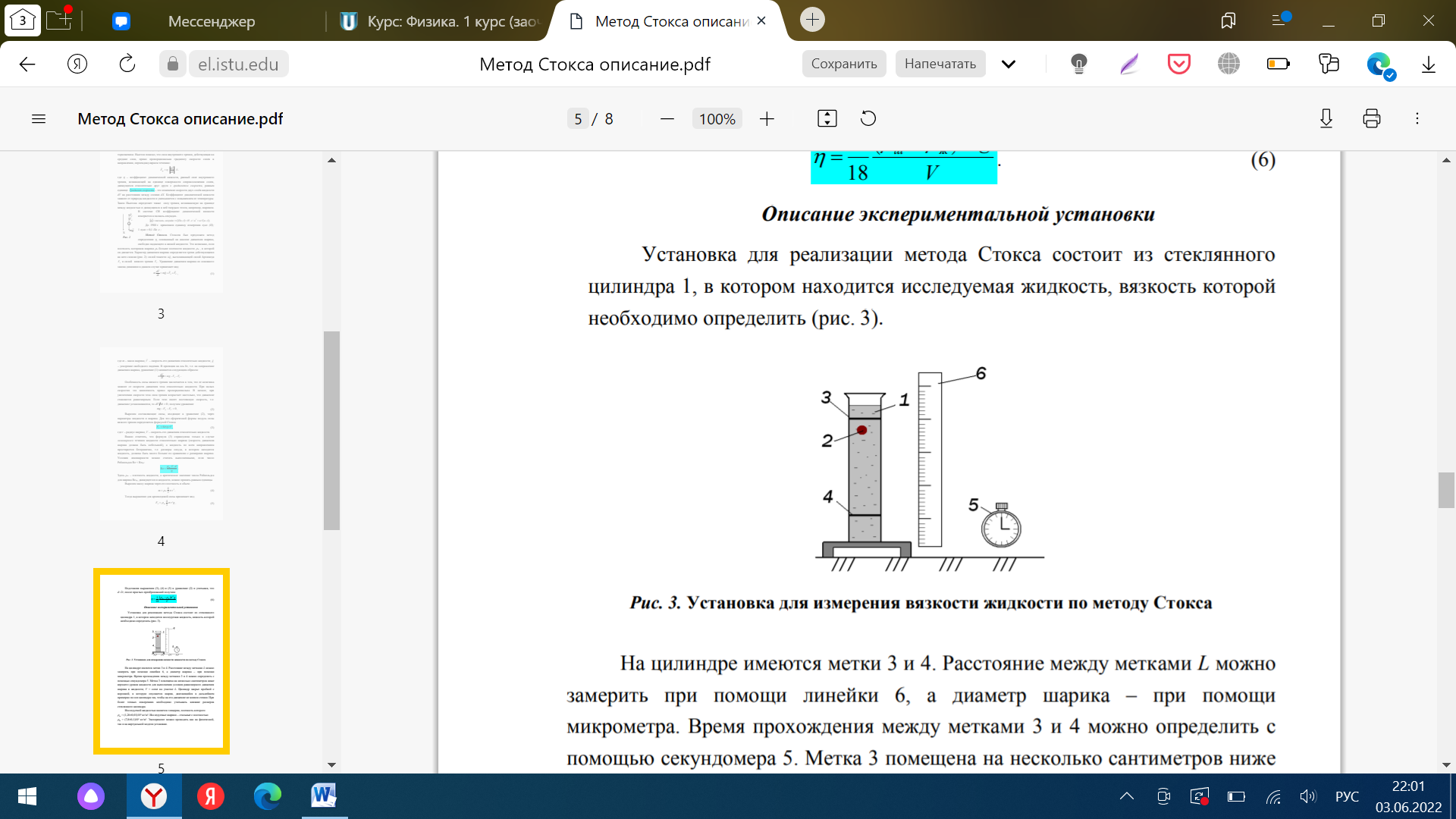 На цилиндре имеются метки 3 и 4. Расстояние между метками L можно замерить при помощи линейки 6, а диаметр шарика – при помощи микрометра. Время прохождения между метками 3 и 4 можно определить с помощью секундомера 5. Метка 3 помещена на несколько сантиметров ниже верхнего уровня жидкости для выполнения условия равномерного движения шарика в жидкости; V = const на участке L. Цилиндр закрыт пробкой с воронкой, в которую опускается шарик, двигающийся в дальнейшем примерно по оси цилиндра так, чтобы на его движение не влияли стенки. При более точных измерениях необходимо учитывать влияние размеров стеклянного цилиндра. Исследуемой жидкостью является глицерин, плотность которого ж = (1,260,01)103 кг/м3 . Исследуемые шарики – стальные с плотностью ш = (7,80,1)103 кг/м3 . Рабочая формула. Если в выражении скорость равномерного движения шарика в жидкости V заменить отношением L/t, то получим: 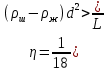 Порядок выполнения работы 1. Получить свой вариант задания и допуск к работе у ведущего преподавателя. Свой вариант (значения L и d) можно взять из таблицы в приложении по номеру зачётной книжки. 2. Познакомиться с работой виртуальной лабораторной установки. 3. Провести пробные измерения для различных значений диаметра шарика d и расстояния между метками L, определяя время прохождения между метками при помощи секундомера. 4. Занести в таблицу заданные в вашем варианте значения: расстояние Li между метками 3 и 4 (см. рис.3), диаметр шарика di и его плотность ш, а также плотность исследуемой жидкости ж. 5. Сбросить шарик в сосуд с жидкостью. В момент касания шариком верхней метки запустить секундомер, а в момент касания шариком нижней метки остановить его. Записать в таблицу показание секундомера ti. 6. Кнопкой “СБРОС” установить нуль на табло секундомера. 7. Повторить измерения пять раз, задавая различные значения диаметра шариков di и расстояние Li между метками (пункт 3 и 4). 8. Результаты опытов занесите в таблицу измерений. 9. Вычислить коэффициент вязкости для каждого из пяти опытов по рабочей формуле. 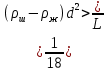 10. Найти среднее значение коэффициента вязкости : 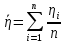 11.Определить абсолютные приборные погрешности прямых измерений (расстояния между метками L, диаметра шарика d, времени его падения t, плотности шарика ш и жидкости ж). 12.Оценить полную абсолютную . 13. Записать конечный результат в виде . 14. Сравнить полученное значение со справочными данными. 15.По результатам эксперимента сделать выводы. Таблица измерений
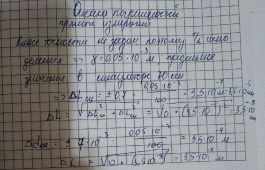 Для определения случайной погрешности измерений коэффициента вязкости составим табл. 2, в которую занесём результаты измерений, промежуточные вычисления и другие необходимые данные для подстановки их в формулу Абсолютные погрешности отдельных измерений периода, находим по формуле i = 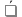 - i и заносим в табл. 2. - i и заносим в табл. 2.Таблица 2
i = 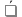 - i = 1,475-1,52= -0,045 с и тд - i = 1,475-1,52= -0,045 с и тд  tp,n* tp,n*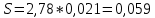 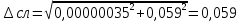 Па*с Па*с 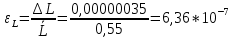 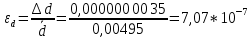 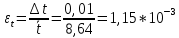 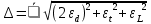 = 1,475*0,0115=0,017 = 1,475*0,0115=0,017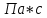 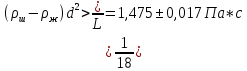 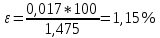 По табличным данным, вязкость глицерина 1,5 Па*с, что говорит о правильности измерения. В результате проведенного лабораторного эксперимента определили коэффициент вязкости  =1,475±0,017 =1,475±0,017 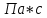 с надёжность 95 % при числе измерений n = 5 и относительной погрешности 1,15%. с надёжность 95 % при числе измерений n = 5 и относительной погрешности 1,15%. Оценка погрешностей показывает, что при использовании данного метода случайная погрешность измерений превышает погрешность средств измерений. Истинное (табличное) значение величины  1,5 1,5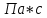 попадает в полученный доверительный интервал. попадает в полученный доверительный интервал.Контрольные вопросы Поясните сущность явления вязкого трения. Какова природа сил внутреннего трения жидкости? Вязкость или внутреннее трение – свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одной их части относительно другой. Это явление определяет диссипацию (поглощение) энергии при деформации среды. При деформации сдвига вязкость называют сдвиговой. При деформации объема (всестороннее сжатие) проявляется объемная вязкость. В данном случае мы будем касаться только вопроса сдвиговой вязкости. Суть явления состоит в том, что движущиеся слои газа или жидкости увлекают соседние слои и, наоборот, неподвижные (или движущиеся с меньшей скоростью) тормозят более быстрые соседние слои. Таким образом, между любыми соседними слоями рассматриваемой среды действуют силы внутреннего трения (или силы вязкости). Механизм возникновения этих сил заключается в переносе импульса (количества движения) от одного слоя к другому. Что такое коэффициент динамической вязкости? В каких единицах измеряется величина вязкости в системе СИ? Коэффициентом динамической вязкости называется величина, численно равная силе внутреннего трения, с которой один слой увлекает или тормозит другой слой жидкости при условии, что площадь соприкосновения слоев и градиент скорости . В системе СИ за единицу динамической вязкости принимают - вязкость такой среды, в которой один слой увлекает или тормозит другой с силой в , если площадь соприкосновения слоев и градиент скорости . Какие силы действуют на тело, движущееся в жидкости? На тело, погруженное в жидкость и остающееся в равновесии на плаву действуют две силы: сила тяжести и равная ей выталкивающая сила (и равная весу жидкости, вытесненной погруженным объёмом тела) . На тело, погруженное в жидкость и тонущее действуют три силы: сила тяжести, неравная ей (меньше) выталкивающая сила (равная весу жидкости, вытесненной погруженным объёмом тела) , а также сила трения при движении, в значительной степени зависящая от скорости погружения и вязкости жидкости. На тело, погруженное в жидкость и лежащее плотно на дне, действуют три силы: сила тяжести, неравная ей выталкивающая сила, и сила реакции со стороны дна. В данном случае выталкивающая сила уменьшается на величину, равную весу жидкости, занимаемому той частью объёма тела, под которой нет воды Дайте определение ламинарного и турбулентного течения жидкости. Турбулентным называется такое течение жидкости, при котором её частицы совершают неустановившееся и неупорядоченные движения по сложным траекториям, приводящим к перемешиванию слоёв. Ламинарное – это упорядоченное течение жидкости, при котором траектории движения соседних частиц мало отличаются друг от друга Запишите формулу Стокса и укажите условия ее применимости. Для тел сферической формы модуль силы вязкого трения определяется формулой Стокса F = 6πηrv где r – радиус шарика; V – скорость его движения относительно жидкости. Важно отметить, что формула справедлива только в случае ламинарного течения жидкости относительно шарика (скорость движения шарика должна быть небольшой), а жидкость по всем направлениям простирается безгранично, т.е. размеры сосуда, в котором находится жидкость, должны быть много больше по сравнению с размерами шарика. Определите величину силы трения, действующей на стальной шарик диаметром 3 мм, падающий со скоростью 0,75 м/с в жидкости с коэффициентом вязкости 1,5 Па. с. F=6*3.14*1.5*0.003*0. 5=0.063 Почему шарик в начале движения ускоряется, а затем движется равномерно? Что такое градиент скорости? В начале движения шарика движение будет ускоренным за счет ускорения свободного падения. С ростом скорости растет и сила сопротивления, а ускорение шарика уменьшается. Наступает такой момент, когда действующие на шарик силы уравновесятся, ускорение станет равным нулю, а движение шарика - равномерным на участке L. Градиент скорости – это изменение скорости двух слоёв жидкости dV на расстоянии между слоями dX. Запишите рабочую формулу, объясните условия её применения и причину начала измерения времени не от поверхности жидкости. dV/dX Верхняя метка помещена на несколько сантиметров ниже верхнего уровня жидкости для выполнения условия равномерного движения шарика в жидкости. |
