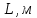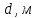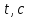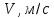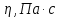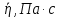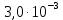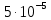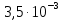Определение коэффициента вязкости жидкости методом Стокса. Лаб_Опред.коэф.вязкости.жид.м.Стокса(L=58-63см,d=3,0-3,5мм) (1).. Лабораторная работа Определение коэффициента вязкости жидкости методом Стокса
 Скачать 86.02 Kb. Скачать 86.02 Kb.
|
|
Лабораторная работа Определение коэффициента вязкости жидкости методом Стокса Цель работы: изучение явления внутреннего трения в жидкостях и опытное определение величины коэффициента вязкости жидкости методом Стокса на виртуальной лабораторной установке. Приборы и принадлежности: цилиндрический сосуд с исследуемой жидкостью, штангенциркуль, секундомер, масштабная линейка, шарики. Виртуальная установка. Теоретическая часть: 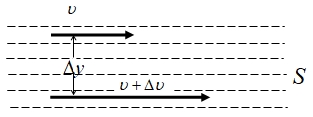 Явлением внутреннего трения (вязкости) называется появление сил трения между слоями жидкости (или газа) движущимися друг относительно друга параллельно и с разными по величине скоростями. Явлением внутреннего трения (вязкости) называется появление сил трения между слоями жидкости (или газа) движущимися друг относительно друга параллельно и с разными по величине скоростями. Рис.1 движение тела При движении плоских слоев сила трения между ними согласно закону Ньютона равна: 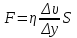 где - коэффициент пропорциональности, называемый коэффициентом вязкости или динамической вязкостью; S - площадь соприкосновения слоев, где - коэффициент пропорциональности, называемый коэффициентом вязкости или динамической вязкостью; S - площадь соприкосновения слоев,  - разница в скорости между соседними слоями, - разница в скорости между соседними слоями, 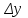 - расстояние между соседними слоями. - расстояние между соседними слоями.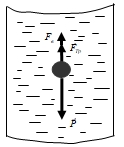 Отсюда η численно равен тангенциальной силе, приходящейся на единицу площади соприкосновения слоев, необходимой для поддержания разности скоростей, равной единице, между двумя параллельными слоями вещества, расстояние между которыми равно единице. В СИ единица вязкости - паскаль·секунда. Отсюда η численно равен тангенциальной силе, приходящейся на единицу площади соприкосновения слоев, необходимой для поддержания разности скоростей, равной единице, между двумя параллельными слоями вещества, расстояние между которыми равно единице. В СИ единица вязкости - паскаль·секунда. Рис.2 схема установки Пусть в заполненном жидкостью сосуде движется шарик, размеры которого значительно меньше размеров сосуда. На шарик действуют три силы: сила тяжести Р, направленная вниз; сила внутреннего трения 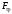 и выталкивающая сила Fв, направленные вверх. Шарик сначала падает ускоренно, но затем очень быстро наступает равновесие, так как с увеличением скорости растет и сила трения. Стокс же показал, что эта сила при малых значениях скорости пропорциональна скорости движения шарика v и его радиусу r: и выталкивающая сила Fв, направленные вверх. Шарик сначала падает ускоренно, но затем очень быстро наступает равновесие, так как с увеличением скорости растет и сила трения. Стокс же показал, что эта сила при малых значениях скорости пропорциональна скорости движения шарика v и его радиусу r:  , где - коэффициент вязкости. , где - коэффициент вязкости. Основные расчетные формулы: 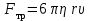 , где , где 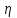 - коэффициент вязкости, r- радиус шарика, - коэффициент вязкости, r- радиус шарика,  - скорость движения шарика; - скорость движения шарика;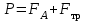 , где Р- сила тяжести, действующая на шарик, FА- сила Архимеда, Fтр- сила внутреннего трения; , где Р- сила тяжести, действующая на шарик, FА- сила Архимеда, Fтр- сила внутреннего трения;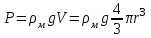 , где м - плотность материала шарика; V – объем шарика; , где м - плотность материала шарика; V – объем шарика;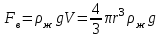 , где , где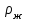 - плотность жидкости; - плотность жидкости;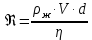 – число Рейнольдса, – число Рейнольдса, 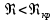 , , 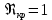 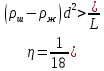 Формула расчета средней квадратичной погрешности: 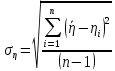 , , где  среднее значение коэффициента вязкости, среднее значение коэффициента вязкости, 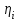 - значение коэффициента вязкости в каждом отдельном опыте, n- количество опытов. - значение коэффициента вязкости в каждом отдельном опыте, n- количество опытов.Экспериментальная часть: Выполним экспериментальную часть задания и заполним таблицу 1 измерениями и вычислениями. Даны измерения: 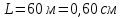 , остальные значения в диапазоне , остальные значения в диапазоне 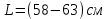 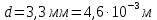 , остальные значения в диапазоне , остальные значения в диапазоне 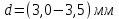 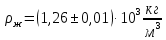 - плотность глицерина - плотность глицерина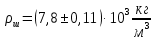 - плотность стальных шариков - плотность стальных шариковТаблица 1.Таблица измерений и вычислений
Вычислим скорость падения шарика для каждого опыта по формуле: 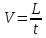 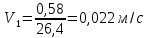     Вычислим значение коэффициента вязкости для каждого опыта по формуле: 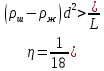 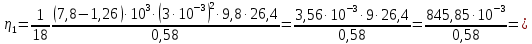 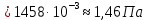 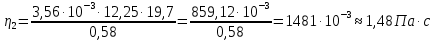  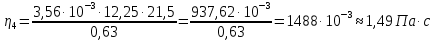 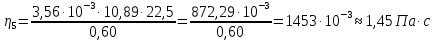 Вычислим среднее значение коэффициента вязкости по формуле: 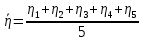 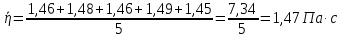 Вычислим число Рейнольдса 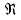 для каждого опыта по формуле: для каждого опыта по формуле: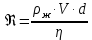 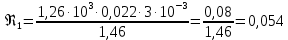  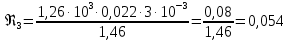 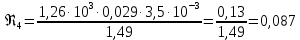 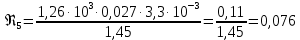 Определим абсолютные приборные погрешности прямых измерений (расстояния между метками 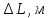 , диаметра шарика , диаметра шарика 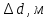 , времени его падения , времени его падения  , плотности шарика , плотности шарика 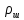 и жидкости и жидкости 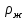 ), а также их относительные ошибки εL, εd, и εt. ), а также их относительные ошибки εL, εd, и εt. Приборная погрешность  Приборная погрешность 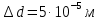 Приборная погрешность 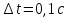 Приборная погрешность 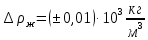 - плотность глицерина - плотность глицеринаПриборная погрешность 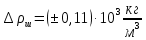 - плотность стальных шариков - плотность стальных шариковОтносительная ошибка измерений:  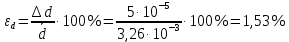 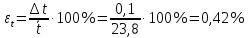  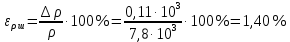 Оценим полную абсолютную 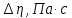 и относительную и относительную  погрешности: погрешности:Рассчитаем 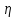 с учетом доверительных погрешностей (коэффициента Стьюдента): с учетом доверительных погрешностей (коэффициента Стьюдента):   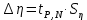 , где , где 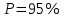 - доверительная вероятность, - доверительная вероятность,  - число опытов, - число опытов,  , ,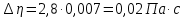 , тогда , тогда 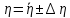 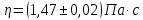 - с учетом доверительных погрешностей - с учетом доверительных погрешностейРассчитаем 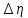 по методике расчёта погрешностей косвенных измерений: по методике расчёта погрешностей косвенных измерений:  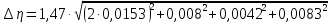 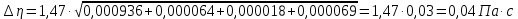 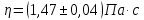 - с учетом погрешностей косвенных измерений - с учетом погрешностей косвенных измеренийВычислим относительную  погрешности: погрешности: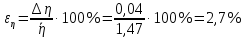 Сравним полученное значение 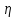 со справочными данными. со справочными данными.В соответствии с табличными данными вязкость глицерина при температуре 20°С составляет 1,48 Па·с, что с учетом приборных погрешностей является измеряемой нами величиной равной 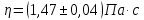 . .Вывод: в ходе выполнения лабораторной работы были изучены явления внутреннего трения в жидкостях и экспериментально определена величина коэффициента вязкости жидкости методом Стокса на виртуальной лабораторной установке. Путем постановки 5 опытов (для наибольшей точности) со стальными шариками (различного диаметра), удалось установить, что скорость шарика, движущегося в сосуде с жидкостью, зависит от размеров шарика. В результате получили среднее значение вязкости жидкости (глицерина) 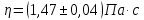 . Полученный результат имеет небольшую погрешность . Полученный результат имеет небольшую погрешность 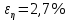 , что позволяет говорить о точности расчетной формулы и о незначительных приборных погрешностях при измерениях и вычислениях. Относительно табличных значений вязкости глицерина искомая величина вычислена верно и подтверждена экспериментально. , что позволяет говорить о точности расчетной формулы и о незначительных приборных погрешностях при измерениях и вычислениях. Относительно табличных значений вязкости глицерина искомая величина вычислена верно и подтверждена экспериментально. |