Главная страница
Навигация по странице:

  • ОТЧЕТ По лабораторная работапо дисциплине «Основы передачи данных »По теме«Исследование методов контроля и коррекции ошибок

  • Целью работы

    		•

    лаб4 Нгуен- Зунг м30-302бки. Лабораторная работа по дисциплине Основы передачи данных


    Скачать 188.47 Kb.
    НазваниеЛабораторная работа по дисциплине Основы передачи данных
    Дата26.06.2021
    Размер188.47 Kb.
    Формат файлаdocx
    Имя файлалаб4 Нгуен- Зунг м30-302бки.docx
    ТипЛабораторная работа
    #221815

    МОСКОВСКИЙ АВИАЦИОННЫЙ ИНСТИТУТ

    (НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ)

    «МАИ»

    _____________________________________________________________________________

    Институт №3 «Системы управления, информатика и электроэнергетика»

    Кафедра 301 «Системы автоматического и интеллектуального управления»


    ОТЧЕТ

    По лабораторная работа

    по дисциплине «Основы передачи данных»

    По теме

    «Исследование методов контроля и коррекции ошибок

    при передаче данных»

    Выполнил:

    студент группы М3О-302Бки

    Чинь Динь Нгуен.

    Буй Чунг Зунг

    Преподаватель:

    преподаватель каф. №301

    Макаренкова Н.А.


    Москва, 2021

    Целью работы является изучение методов и средств контроля и коррекции одиночных ошибок при передаче данных

    Варианты заданий Число информационных разрядов в слове = 11

    При заданных четырех информационных битах (d1, d2, d3, d4,...,d11) полагаем первые четыре бита кодового слова равными эти четырем информационным битам (p1, p1, p3, p4)

    p1=d1+d2+d4+d5+d7+d9+d11

    p2=d1+d3+d4+d6+d7+d10+d11

    p3=d2+d3+d4+d8+d9+d10+d11

    p4=d5+d6+d7+d8+d9+d10+d11

    Здесь + обозначает сложение по модулю 2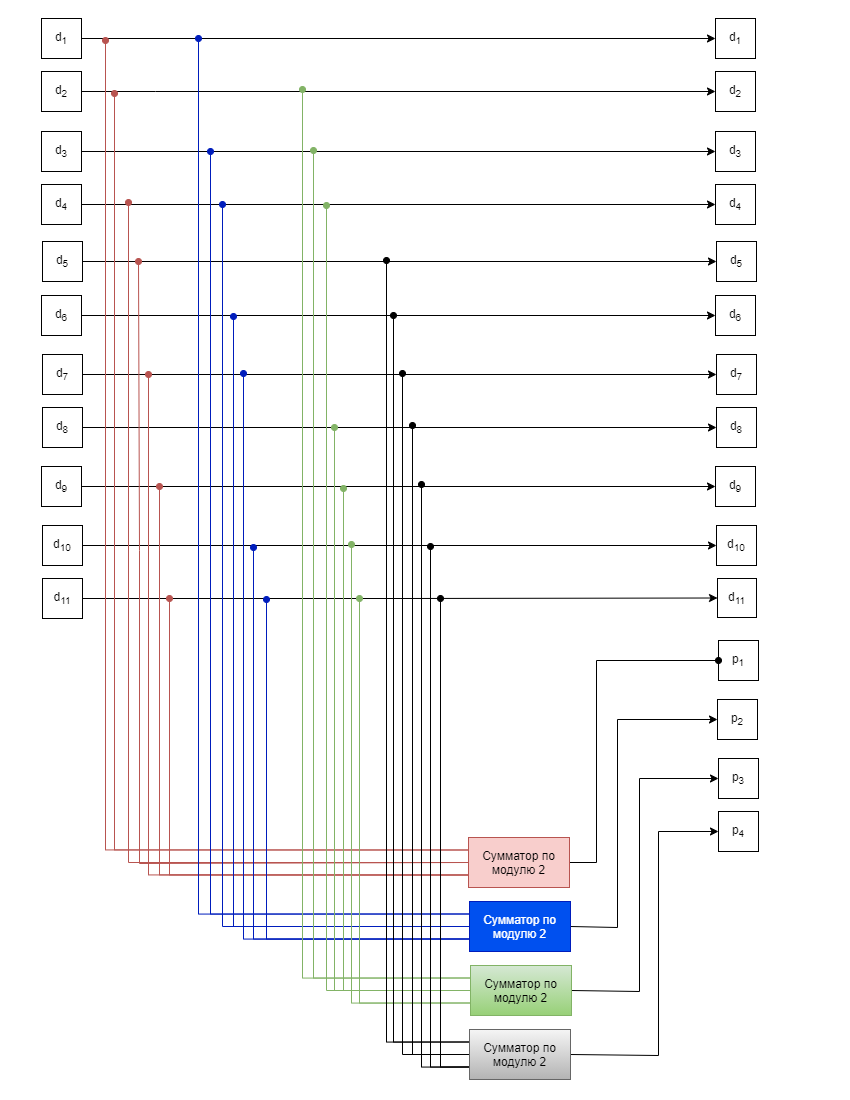



    Рис 1. Реализация (15, 11) кода Хэмминга

    При получении 15-битовое слово ( d1’, d2’, …., d11’, p1’, p2, p3’, p4’)

    Тогда получается синдром (s1,s2,s3,s4)

    s1=p1’+ d1’+d2’+d4’+d5’+d7’+d9’+d11’

    s2=p2’+ d1’+d3’+d4’+d6’+d7’+d10’+d11’

    s3 = p3’+ d2’+d3’+d4’+d8’+d9’+d10’+d11’

    s4 = p4’ + d5’+d6’+d7’+d8’+d9’+d10’+d11’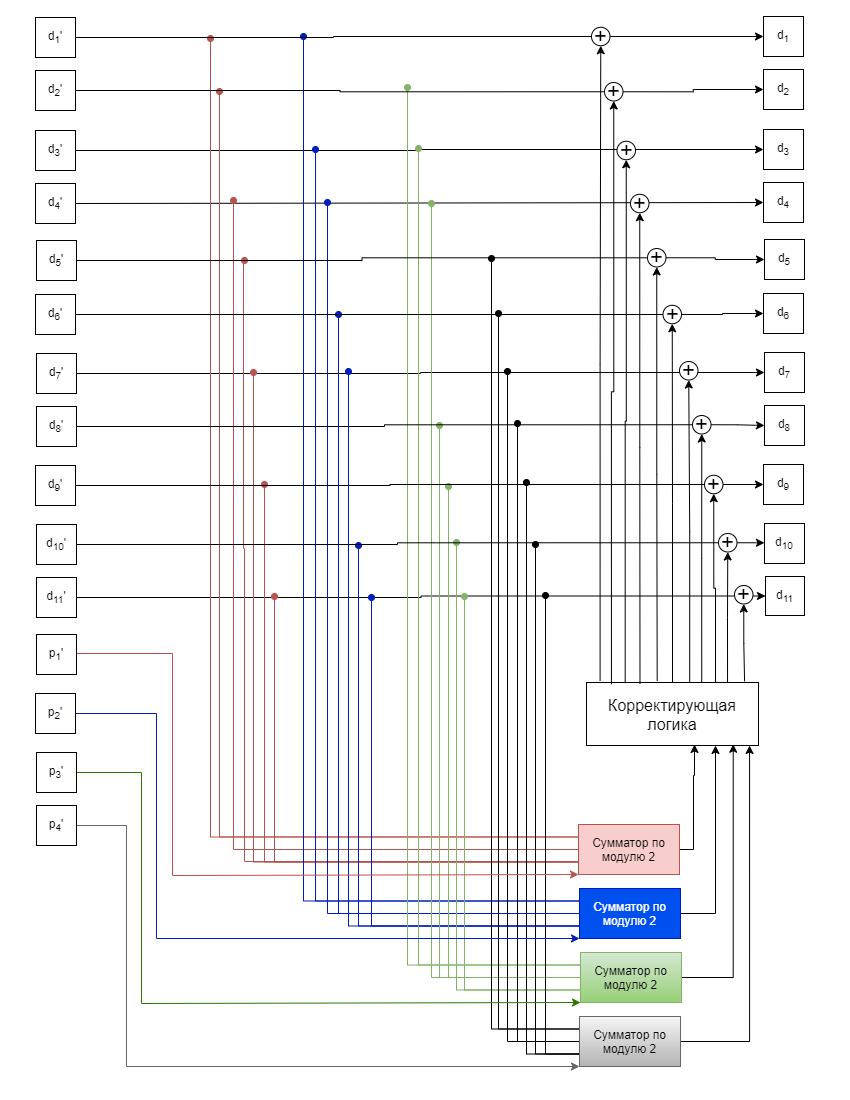



    Рис 2. Реализация (15, 11)декодера Хэмминга


    s4
    s3
    s2
    s1
    позиция ошибки

    0
    0
    0
    0
    нет



    0
    0
    0
    1
    1
    p1

    0
    0
    1
    0
    2
    p2

    0
    0
    1
    1
    3
    d1

    0
    1
    0
    0
    4
    p3

    0
    1
    0
    1
    5
    d2

    0
    1
    1
    0
    6
    d3

    0
    1
    1
    1
    7
    d4

    1
    0
    0
    0
    8
    p4

    1
    0
    0
    1
    9
    d5

    1
    0
    1
    0
    10
    d6

    1
    0
    1
    1
    11
    d7

    1
    1
    0
    0
    12
    d8

    1
    1
    0
    1
    13
    d9

    1
    1
    1
    0
    14
    d10

    1
    1
    1
    1
    15
    d11

    Таблица 1. Таблица синдромов
    Ааналог этого процесса можно сделать в среде Microsoft Excel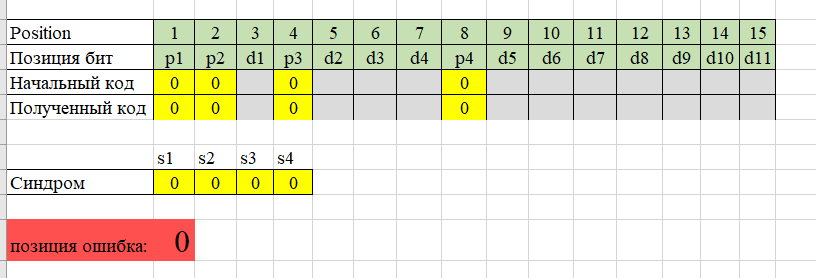



    При заданной код 10010111001 мы получим код Хемминга: 001000110111011


    Задав одну ошибку, на бите d4 (position 7), сразу получилось сообщенниеб что позиция ошибки в 7-йо (d4)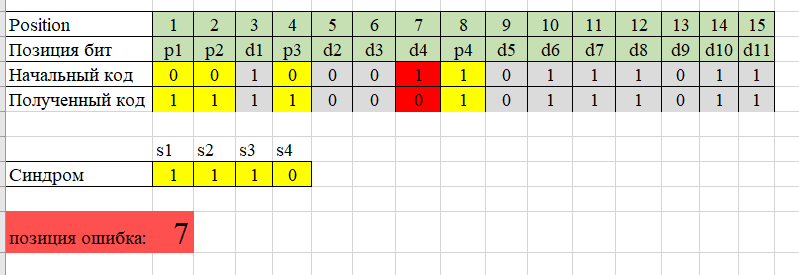



    Задав две ошибки, на битах d4, d8 ( position 7 и 12)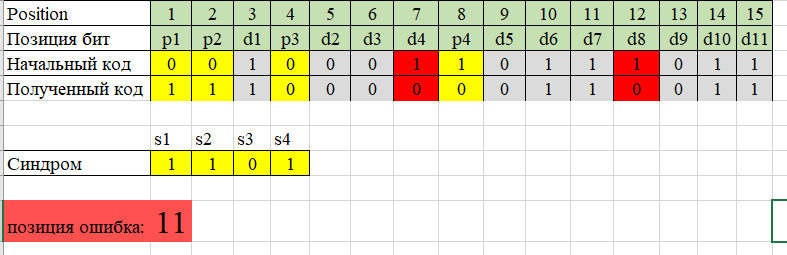



    Получим, что ошибка в 11-ой позиции. Так не верно
    Результат: код Хемминга кооректирует только 1 неправильный бит!!!!

    написать администратору сайта