5-Лабораторная работа (Физика) (Изучение затухающих электромагн. Лабораторная работа по курсу "Общая физика" изучение затухающих электромагнитных колебаний

• Название: Лабораторная работа по курсу "Общая физика" изучение затухающих электромагнитных колебаний
• Дата: 18.01.2023
• Размер: 360.5 Kb.
• Имя файла: 5-Лабораторная работа (Физика) (Изучение затухающих электромагн.doc
• Тип: Лабораторная работа; #892566

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)


Кафедра физики

ОТЧЕТ

Лабораторная работа по курсу "Общая физика"


ИЗУЧЕНИЕ ЗАТУХАЮЩИХ ЭЛЕКТРОМАГНИТНЫХ КОЛЕБАНИЙ
Преподаватель Студент группы

___________ / Васильев Н.Ф. / __________ / /
___________2007 г. 1 июля 2007 г.

Томск 2007

1. ЦЕЛЬ РАБОТЫ
Целью данной работы является изучение работы колебательного контура, свободных затухающих электромагнитных колебаний и их характеристик.
2. ОПИСАНИЕ УСТАНОВКИ И МЕТОДИКИ ЭКСПЕРИМЕНТА
С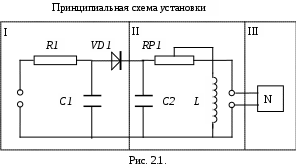
хема установки представлена на рис. 2.1.. Колебания в контуре II возбуждаются с помощью генератора импульсного напряжения, вырабатываемого в контуре I, собранного на резисторе R₁ , емкости C₁ и диоде VD₁ ( в качестве генератора импульсного напряжения можно использовать стандартный генератор импульсов или генератор релаксационных колебаний).

Схема смонтирована на съемной панели лабораторного макета. В качестве резистора RP₁ в колебательном контуре II используется переменное сопротивление, максимальное значение которого RP₁ = 400 Ом устанавливается поворотом ручки потенциометра по часовой стрелке в крайнее положение. При повороте ручки против часовой стрелки в крайнее положение значение сопротивления RP₁= 0. В этом случае активное сопротивление колебательного контура R складывается из сопротивления соединительных проводов контура и активного сопротивления катушки индуктивности. Возбуждение контура производится периодически от генератора импульсного напряжения I, регистрируются колебания на осциллографе III. Каждый импульс, подаваемый с генератора на колебательный контур, возбуждает один цуг колебаний.

Измерения амплитуды и периода колебаний осуществляются непосредственно с помощью осциллографа.
3. ОСНОВНЫЕ РАСЧЕТНЫЕ ФОРМУЛЫ
Значения логарифмического декремента затухания:

, (3.1)

где n - номер измерений амплитуды.
Среднеарифметическое значение логарифмического декремента затухания:

(3.2)

Амплитуда в момент времени

, (3.3)

где - коэффициент затухания.

Коэффициент затухания: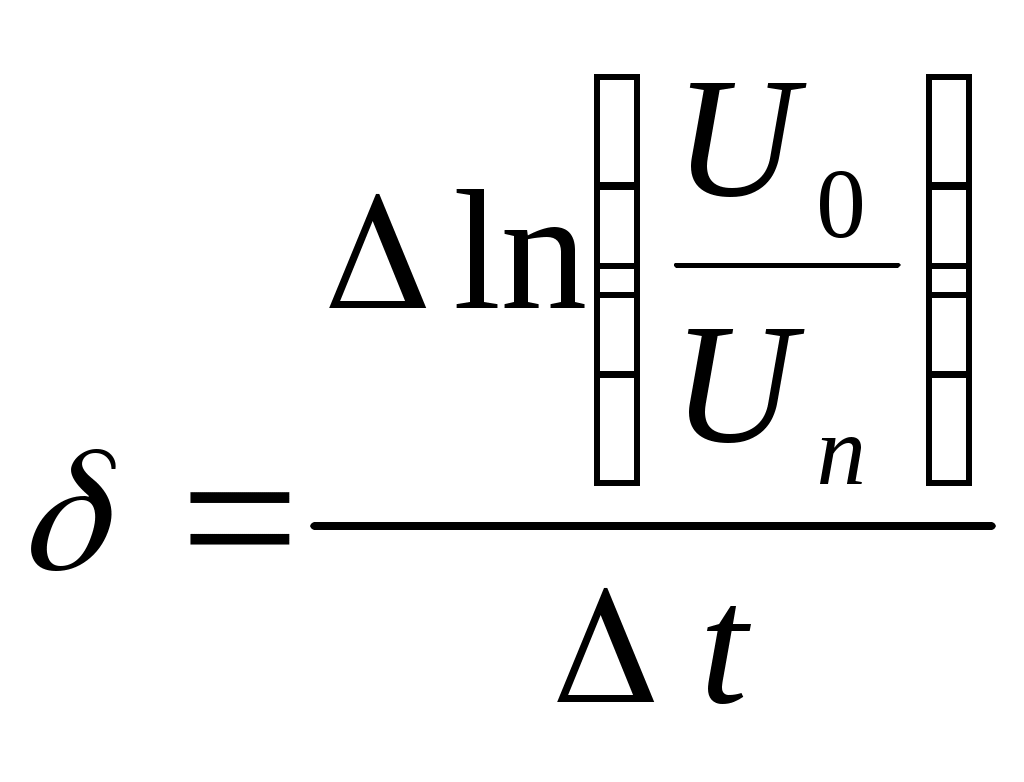

_(3.4)
Собственная частота контура:

_(3.5)

Частота затухающих колебаний контура:

_(3.6)

Период колебаний:

_(3.7)

Критическое сопротивление:

_(3.8)

Добротность контура:

_(3.9)

4. РЕЗУЛЬТАТЫ РАБОТЫ И ИХ АНАЛИЗ
Экспериментальные данные и результаты их обработки представлены в следующей таблице.

Таблица

Результаты прямых и косвенных измерений.

Значение активного сопротивления контура R	Номер измеряемой амплитуды n	Значение амплитуды Un, мм (дел.)	Значение логариф-мического декремента затухания 	Среднее значение <>		Период затухающих колебаний T, c
R = Rх	1 2 3 4 5	29,1 25,6 22,6 19,9 17,5	— 0,1282 0,1246 0,127 0,1285	0,127075	0,127 0,255 0,3798 0,507 0,6355	0.986·10-3
R = Rx+ RP1	1 2 3 4 5	26,8 17,1 11,0 7,0 4,5	— 0,4493 0,4412 0,452 0,442	0,446125	0,446 0,896 1,337 1,789 2,231	0.988·10-3

Найдем значение логарифмического декремента затухания: для этого знать значения амплитуд колебания, найдем их.

При :

1. 29.1·0.5=14.55 В,

2. 25.6·0.5=12.8 В,

3. 22.6·0.5=11.3 В,

4. 19.9·0.5=9.95 В,

5. 17.5·0.5=8.75 В.

При :

1. 26.8·0.5=13.4 В,

2. 17.1·0.5=8.55 В,

3. 11·0.5=5.5 В,

4. 7·0.5=3.5 В,

5. 4.5·0.5=2.25 В.

Теперь рассчитываем логарифмический декремент затухания по формуле 3.1:

При :

1. 0.1282

2. 0.1246

3. 0.127

4. 0.1285

При :

1. 0.4493

2. 0.4412

3. 0.452

4. 0.442

Занесем полученные данные в таблицу №1.

Теперь найдем среднее арифметическое значений логарифмического декремента затухания по формуле 3.2:

При :



При :



Занесем полученные данные в таблицу №1.

Следующая неизвестная величина – это выражение 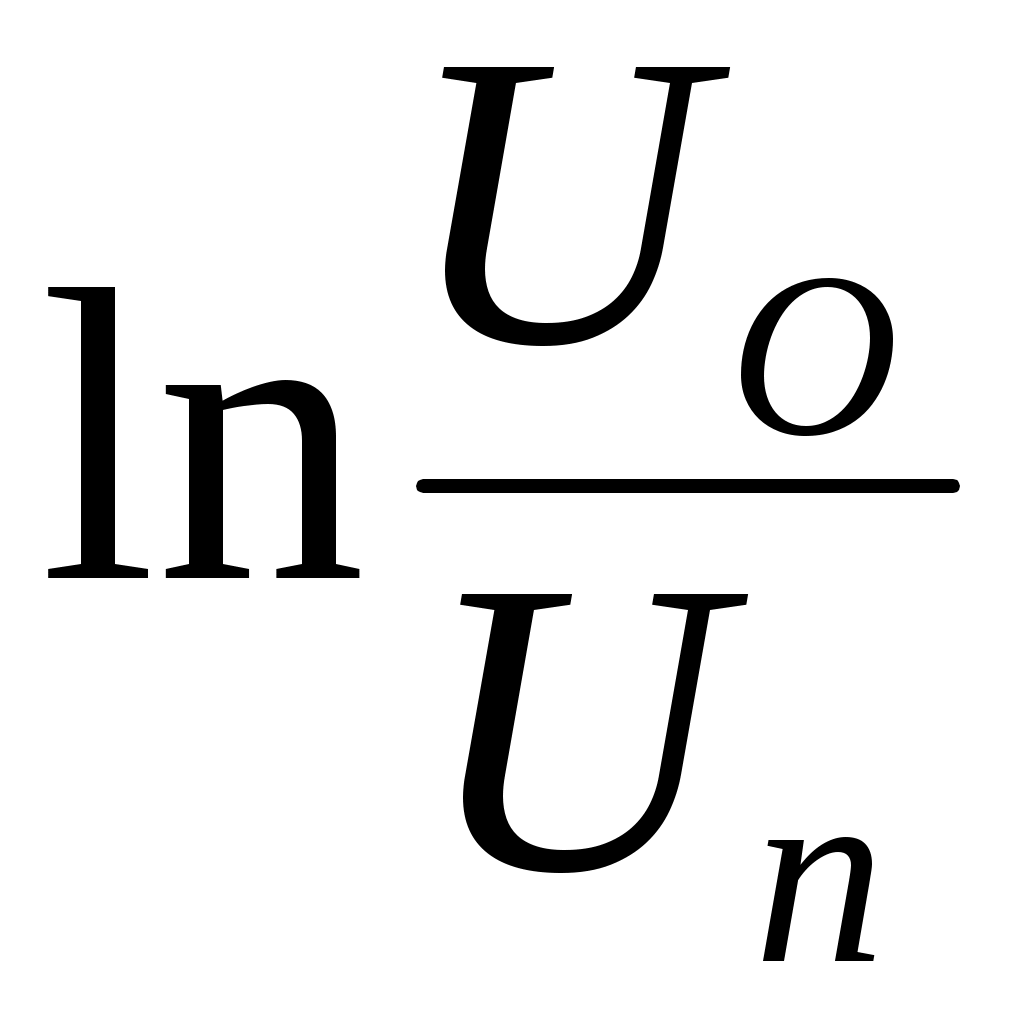, в которой нам неизвестно значение ( - это значение амплитуды в момент времени ). Найдем по формуле 3.3:

При :



При :


Теперь найдем значения выражения :

При :

1. = 0.127

2. = 0.255

3. = 0.3798

4. = 0.507

5. = 0.6355

При :

1. = 0.446

2. = 0.896

3. = 1.337

4. = 1.7889

5. = 2.231

Занесем полученные данные в таблицу №1.

Рассчитаем период затухающих колебаний:

При :



При :



Занесем полученные данные в таблицу №1.

Найдем время n-го колебания по формуле (это надо для построения графика):

При :

1. 1· = ,

2. 2· =1.972 ,

3. 3· =2.958 ,

4. 4· =3.944 ,

5. 5· =4.93 .

При :

1. 1· =0.988 ,

2. 2· =1.976 ,

3. 3· =2.964 ,

4. 4· =3.952 ,

5. 5· =4.94 .

Построим графики зависимостей для (Рис. 1) и (Рис. 2) в отдельности. Для построения графика занесем данные о точках графиков в таблицу №2.

Таблица №2

		, с
При	0,127 0,255 0,3798 0,507 0,6355	0.986·10-3 1.972·10-3 2.958·10-3 3.944·10-3 4.93·10-3
	0,446 0,896 1,337 1,789 2,231	0.988·10-3 1.976·10-3 2.964·10-3 3.952·10-3 4.94·10-3

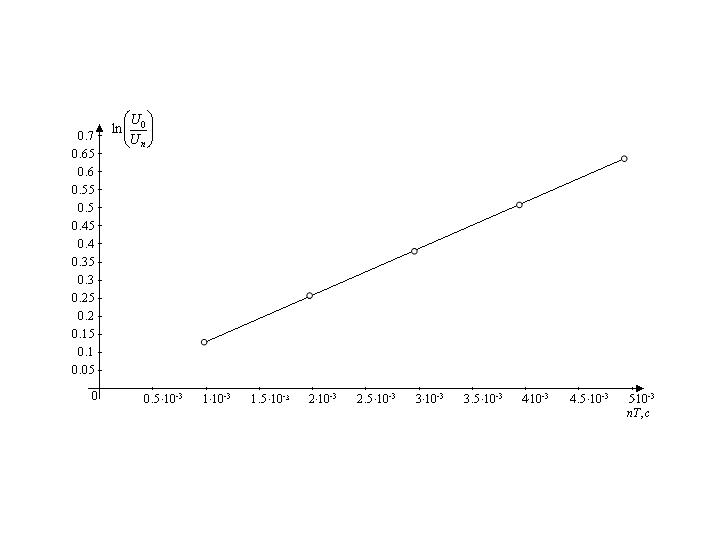Рис. 1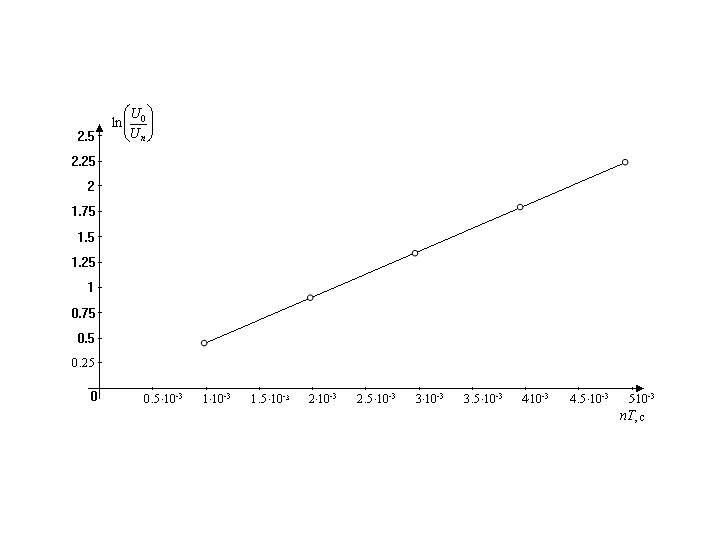


Рис. 2
Определим для каждого из графиков коэффициент затухания по формуле 3.4:

Для рис. 1: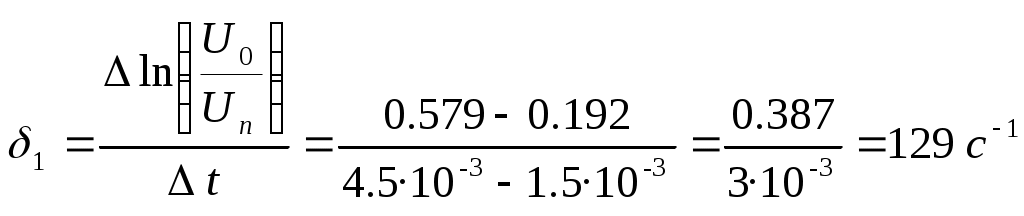



Для рис. 2: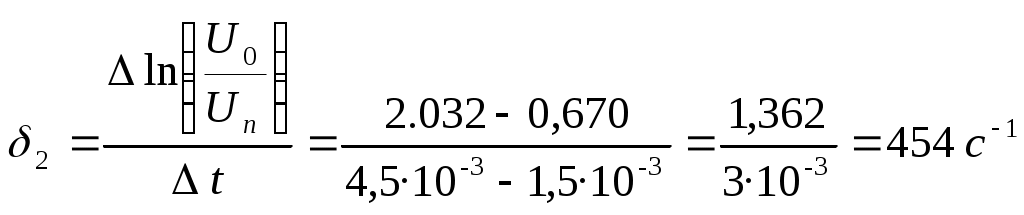



Теперь нам надо найти индуктивность L и суммарное активное сопротивление R_x. Находим их из формул для коэффициента затухания: , .



.

Теперь рассчитаем R_x по формуле :

.

Теперь рассчитаем собственную частоту контура по формуле 3.5 (учитывая, что С=0.04 мкФ):



_{Теперь найдем частоту затухающих колебаний контура по формуле 3.6:}

При :



При :



_{Рассчитаем по формуле 3.7 период колебаний:}

При :



При :



_{Теперь рассчитаем по формуле 3.8 критическое сопротивление:}

.

Рассчитаем значение добротности контура по формуле 3.9:

При :


При :

_.

5. ВЫВОДЫ

В результате проделанной работы, мы изучили работу колебательного контура и определили основные характеристики свободных затухающих колебаний, а также убедились в справедливости экспоненциального закона убывания амплитуды со временем, так как построили линеаризованные графики зависимости для двух значений активного сопротивления контура и определили из них коэффициенты затухания, равные 129с^-1 и 454с^-1. Также мы рассчитали: индуктивность ( ),собственную частоту контура ( ), частоты затухающих колебаний контура ( ), периоды колебаний ( ), критическое сопротивление ( ), добротность контура ( ).

6. 
   КОНТРОЛЬНЫЕ ВОПРОСЫ
   

6.1. Какова цель работы?

Изучение работы колебательного контура и основных характеристик затухающих колебаний; исследование влияния активного сопротивления контура на характер затухания колебаний и проверка справедливости экспоненциального закона убывания амплитуды со временем.

6.2. С помощью, какой системы можно получить свободные электромагнитные колебания?

С помощью колебательного контура.

6.3. К изменению, каких характеристик колебаний приведет увеличение активного сопротивления в колебательном контуре?

К изменению коэффициента затухания, частоты свободных затухающих колебаний, периода колебаний, добротности контура, логарифмического декремента затухания

6.4. Какое, условие необходимо выполнить при подборе элементов (R, L, С) для колебательного контура, чтобы изменение напряжения на предварительно заряженном конденсаторе осуществлялось по колебательному закону ?

, или , где – критическое сопротивление, при котором процесс становится апериодическим.

6.5. Каким образом в данной работе подтверждается правильность вывода об экспоненциальном уменьшении амплитуды напряжения со временем?

Правильность вывода об экспоненциальном уменьшении амплитуды со временем подтверждается построением линейных графиков зависимости .

6.6. Как в данной работе определяется коэффициент затухания?

Коэффициент затухания определяется из графика, как угловой коэффициент прямой, т.е. .

6.7. Какими параметрами контура определяется частота собственных колебаний?

Индуктивностью L и ёмкостью C.
6.8. Как соотносится между собой частота собственных колебаний контура и частота затухающих колебаний?



6.9. Изменение, каких физических величин осуществляется в контуре по колебательному закону?

Изменение энергии электрического поля конденсатора, энергии магнитного поля катушки индуктивности, напряжений и токов на элементах контура.

6.10. Как образуются в контуре электромагнитные колебания?

В начальный момент времени с помощью генератора одиночных импульсов конденсатор заряжается до некоторой разности потенциалов Uна его обкладках. При этом обкладкам конденсатора сообщен заряд ± q. Энергия электрического поля конденсатора We - CU²/2.Если теперь генератор отключить, а конденсатор замкнуть на катушку с индуктивностью L то начнется его разрядка и в катушке возникнет ток. Этот возрастающий от нуля ток приводит к возникновению магнитного поля. Следовательно, энергия электрического поля между обкладками конденсатора постепенно переходит в энергию магнитного поля катушки. Когда полностью разрядился конденсатор, то, казалось бы, ток в катушке должен прекратиться. Но уменьшению тока в катушке препятствует явление самоиндукции, поддерживающее ток в прежнем направлении. Этот убывающий ток продолжает переносить заряды от одной обкладки конденсатора к другой в том же направлении и перезаряжает конденсатор. Перезарядка заканчивается, когда ток становится равным нулю. В этот момент энергия магнитного поля катушки переходит в энергию электрического поля конденсатора. В следующий момент начинает разряжаться конденсатор, при этом ток течет в обратном направлении.

Разрядный ток возрастает, пока конденсатор не разрядится полностью, а затем убывает, но вследствие явления самоиндукции снова перезаряжается конденсатор и контур возвращается в исходное состояние. Этим завершается один период колебаний в контуре

6.11. Как влияет коэффициент затухания на условный период затухающих колебаний контура?

Чем больше коэффициент затухания, тем больше условный период затухающих колебаний.

6.12. Как изменяется логарифмический декремент затухания и добротность контура, если известно, что при изменении параметров контура (R, L, С) число колебаний, за которое амплитуда уменьшится в е раз, увеличилось на десять колебаний?

Происходит уменьшение логарифмического декремента затухания и увеличение добротности контура.

6.13. Чем обусловлено затухание колебаний в контуре?

Потерями на нагрев, на излучение электромагнитных колебаний.

6.14. К изменению, каких характеристик колебаний и колебательного контура приведет изменение индуктивности в цепи?

Изменение индуктивности приведёт к изменению логарифмического декремента затухания, добротности, коэффициента затухания, частоты собственных колебаний, частоты свободных затухающих колебаний, условного периода колебаний, критического сопротивления контура.

6.15. Выполняется ли в реальном колебательном контуре закон сохранения электромагнитной энергии?

Не выполняется, так как часть энергии уходит на нагревание проводников и на излучение электромагнитных колебаний.
6.16. Почему при выводе основного уравнения свободных затухающих колебаний в контуре, где протекают переменные токи, используют закон Ома и правила Кирхгофа, полученные для постоянного тока?

Так как размеры контура не слишком велики (L<C/ν), можно считать, что мгновенное значение тока практически одинаково во всех точках контура. Такие токи называют квазистационарными, для них применимы закон Ома и Кирхгофа.

6.17. Как нужно изменить параметры контура, чтобы при однократной зарядке конденсатора разрядка его осуществлялась по апериодическому закону?

Необходимо в контуре увеличить сопротивление R до , т.е. надо увеличить индуктивность, уменьшить ёмкость.

6.18. Какие колебания называются непериодическими и являются ли затухающие колебания периодическими?

Непериодические колебания – колебания, имеющие не повторяющиеся через равные промежутки времени значения физических величин, характеризующих колебательную систему.

Затухающие колебания не являются периодическими, т.к. максимальное значение амплитуды колебаний, достигаемое в некоторый момент времени, в последующем не повторяется.

6.19. Какая характеристика является количественной характеристикой убывания амплитуды затухающих колебаний?

Логарифмический декремент затухания.

6.20. Чему равно время релаксации затухающих колебаний?

Времени, в течение которого амплитуда затухающих колебаний уменьшается в e раз.