Ваа. затухающие колебания. Лабораторная работа по курсу общей физики изучение затухающих электромагнитных колебаний
 Скачать 102.14 Kb. Скачать 102.14 Kb.
|
|
Министерство образования и науки РФ Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР) Кафедра Физики ОТЧЁТ Лабораторная работа по курсу общей физики ИЗУЧЕНИЕ ЗАТУХАЮЩИХ ЭЛЕКТРОМАГНИТНЫХ КОЛЕБАНИЙ Преподаватель Студенты гр. 351-1 __________Д.Б.Золотухин. _________А.Аскаров _________А.Глухих “__” сентябрь 2022г. _________Б.Цыбенжапов 2022 ВВЕДЕНИЕ Целью данной работы является изучение работы колебательного контура, свободных затухающих электромагнитных колебаний и их характеристик. 1 ОПИСАНИЕ ЭКСПИРЕМЕНТАЛЬНОЙ УСТАНОВКИ И МЕТОДИКИ ИЗМЕРЕНИЙ Для возбуждения и поддержания электромагнитных колебаний используют колебательный контур. Принципиальная схема колебательного контура приведена на рисунке 1.1. 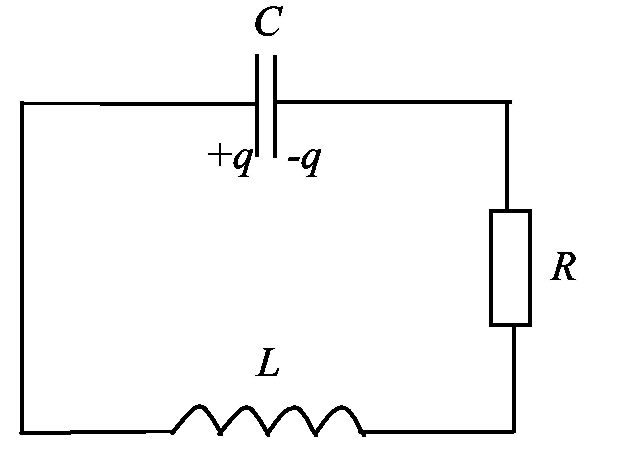 Рисунок 1.1 – Колебательный контур Схема установки представлена на (рис. 1.2). Колебания в контуре II возбуждаются с помощью генератора импульсного напряжения, вырабатываемого в контуре I, собранного на резисторе R1 , емкости C1 и диоде VD1 (в качестве генератора импульсного напряжения можно использовать стандартный генератор импульсов или генератор релаксационных колебаний). 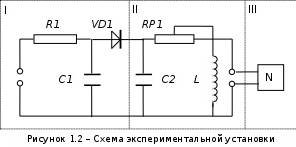 Схема смонтирована на съемной панели лабораторного макета. В качестве резистора RP1 в колебательном контуре II используется переменное сопротивление, максимальное значение которого RP1 = 470 Ом устанавливается поворотом ручки потенциометра по часовой стрелке в крайнее положение. При повороте ручки против часовой стрелки в крайнее положение значение сопротивления RP1= 0. В этом случае активное сопротивление колебательного контура R складывается из сопротивления соединительных проводов контура и активного сопротивления катушки индуктивности. Возбуждение контура производится периодически от генератора импульсного напряжения I, регистрируются колебания на осциллографе III. Каждый импульс, подаваемый с генератора на колебательный контур, возбуждает один цуг колебаний. 2 ОСНОВНЫЕ РАСЧЕТНЫЕ ФОРМУЛЫ Значения логарифмического декремента затухания: 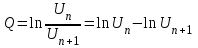  , (2.1) , (2.1) где n - номер измерений амплитуды. 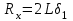  , (2.2) , (2.2)где Rx – активное сопротивление проводника; RP = 141 Ом. 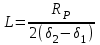  , (2.3) , (2.3)где L – индуктивность контура, 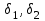  - коэффициенты затухания. - коэффициенты затухания.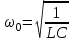  , (2.4) , (2.4)где 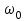  - собственная частота контура; - собственная частота контура; С – емкость конденсатора, C = 0,05*10-6Ф. 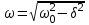  , (2.5) , (2.5)где 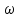  - частота свободных затухающих колебаний. - частота свободных затухающих колебаний.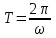  , (2.6) , (2.6)где T – период колебаний. 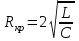  , (2.7) , (2.7)где 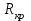  - критическое значение сопротивления. - критическое значение сопротивления.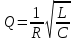  , (2.8) , (2.8)где Q – добротность контура. 3 РЕЗУЛЬТАТЫ РАБОТЫ И ИХ АНАЛИЗ Результаты прямых и косвенных измерений приведены в таблице 3.1. Таблица 3.1 – Результаты прямых и косвенных измерений
Построим графики зависимости 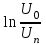  от от 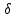  t и проверим справедливость экспоненциального закона убывания амплитуды со временем для первого и второго опыта. В данном случае время удобнее выражать в периодах t = nT. Эта зависимость приведена на рисунках 3.1 (а). t и проверим справедливость экспоненциального закона убывания амплитуды со временем для первого и второго опыта. В данном случае время удобнее выражать в периодах t = nT. Эта зависимость приведена на рисунках 3.1 (а).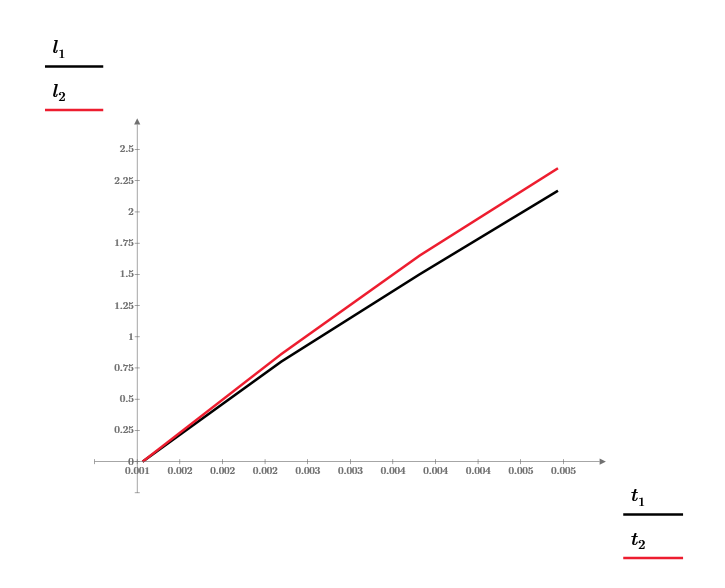 Рисунок 3.1(a) – Зависимость 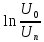 от nT от nTИз графиков определим значения коэффициентов затухания δ1 и δ2 , в которых они являются угловыми коэффициентами прямых. 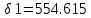 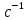 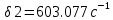 По формуле (2.3) найдем индуктивность контура: 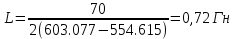 По формуле (2.2) найдем активное сопротивление проводника: 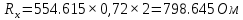 По формуле (2.4) найдем собственную частоту контура: 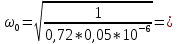 5270 рад/c 5270 рад/cРассчитаем значения частот свободных затухающих колебаний, по формуле (2.5), для двух ситуаций: 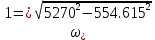 = 5240.8 рад/c = 5240.8 рад/c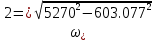 = 5235.4 рад/c = 5235.4 рад/cРассчитаем значения периода колебаний, по формуле (2.6), для двух ситуаций: 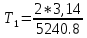 = 1.19* = 1.19*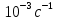 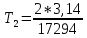 = 1.2* = 1.2*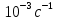 По формуле (2.7) найдем критическое значение сопротивления: 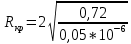 = 7589 Ом = 7589 ОмРассчитаем добротность контура по формуле (2.8), для двух ситуаций: 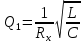 = = 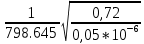 = 4,7 = 4,7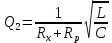 = = 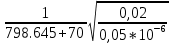 = 4.36 = 4.36ЗАКЛЮЧЕНИЕВ ходе данной работы мы исследовали влияние величины активного сопротивления контура на характер затухания колебаний. Убедились в наличии экспоненциального закона убывания амплитуды со временем. На основе экспериментальных данных определили параметры затухающих колебаний: δ, ω0, ω, T, Rх, Rкр, Q, где Rх – сопротивление соединительных проводов и катушки: 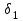  = 554.615 c-1 = 554.615 c-1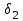  = 603.077 с-1 = 603.077 с-1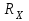  = 798.645 Ом, = 798.645 Ом,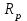  = 70 Ом, = 70 Ом,L = 0,72 Гн, 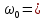 5270 рад/c 5270 рад/c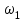  = 5 = 5 240.8 240.8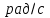 , ,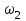  =5235.4 =5235.4 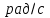  , ,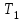  =1.19 мc , =1.19 мc ,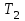  = 1.2 мc, = 1.2 мc,Rкр = 7589 Ом, Q1 = 4.7, Q2 = 4.36. |
