Мат. методы лаба. Лабораторная работа по теме Закон напряжения в проводе
 Скачать 17.14 Kb.
|
|
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Ярославский государственный педагогический университет им. К.Д. Ушинского» Кафедра физики и информационных технологий Лабораторная работа по теме «Закон напряжения в проводе» Выполнил: студент 2 курса физико-математического факультета группы 2607) Гамаев Артём Николаевич Проверил: Иродова И.А Ярославль 2018 Лабораторная работа «Закон напряжения в проводе» Цель работы: найти закон напряжения v (x, t) в любой момент времени. Задача № 164 Напряжение в проводе длинны l в начальный момент одинаково во всех точках провода и равно Е0; ток в начальный момент равен нулю. Омическое сопротивление R, самоиндукция L, утечка за единицу времени G и емкость C в данном проводе связаны соотношением 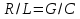 (говорят, что в таком случае мы имеем линию без искажений).Найти напряжение v (x; t) в любой точке провода в любой момент времени  , если левый конец провода (x=0) заземлён, а правый конец (x=l) изолирован.Основные понятия и формулы Провод — электротехническое изделие, служащее для соединения источника электрического тока с потребителем, компонентами электрической схемы. Электри́ческое сопротивле́ние (R) — физическая величина, характеризующая свойства проводника препятствовать прохождению электрического тока и равная отношению напряжения на концах проводника к силе тока, протекающего по нему. Вспомогательная задача № 153 Вывести дифференциальное уравнение, которому удовлетворяет сила тока в тонком проводе, если считать, что омическое сопротивление R, емкость С, утечка (проводимость изоляции) G и самоиндукция L равномерно распределены по длине провода. Здесь R, G, C, L рассчитаны на единицу дины провода; говоря, что эти величины равномерно распределены по длине провода, мы подразумеваем, что R, C, G, L не зависят от того, в какой точке провода мы их рассматриваем. Какой вид будет иметь искомое уравнение в том частном случае, когда R и G столь малы, что ими можно пренебречь (т.е. когда R=0; G=0) Решение задачи № 153 |