интерполяция. лаба-интерполяция. Лабораторная работа. Построение карт геопотенциалов на основе пространственной интерполяции данных локальных измерений

• Название: Лабораторная работа. Построение карт геопотенциалов на основе пространственной интерполяции данных локальных измерений
• Анкор: интерполяция
• Дата: 07.07.2020
• Размер: 1.45 Mb.
• Имя файла: лаба-интерполяция.doc
• Тип: Лабораторная работа; #133959

Лабораторная работа.
Построение карт геопотенциалов на основе пространственной интерполяции данных локальных измерений.
Во многих научных направлениях, занимающихся изучением геосферы Земли, а также в метеорологии, климатологии, экологии, геологии и целом ряде других наук, требуется построение непрерывных функций географических координат (геопотенциалов) по данным локальных измерений (или расчетов) значений этой функции. Примерами могут служить карты среднегодовых температур, среднегодового количества осадков и других метеорологических показателей, которые нельзя непосредственно получить по данным дистанционного зондирования. Аналогичными методами длительное время получали карты рельефа.

С появлением ГИС методы статистического пространственного анализа стали повсеместно применяться в демографических, социологических, маркетинговых и других исследованиях, связанных с анализом пространственно распределенных данных. Область применения методов интерполяции геопространственной информации настолько обширна, что в последнем столетии возникло целое научное направление – геостатистика.

Математический аппарат пространственной интерполяции локальных данных хорошо проработан и довольно разнообразен, именно из-за его повсеместного применения в геофизических исследованиях. В программном инструментарии ГИС он наиболее широко представлен как раз в продуктах линейки ArcGIS. В данной работе Вы познакомитесь с некоторыми из инструментов интерполяции, а также с процедурами, обеспечивающими по результатам интерполяции построение карт геопотенциалов, как в виде растровых слоев, так и виде векторного слоя изолиний (линий равных значений картографируемого геопотенциала).
Методы пространственной интерполяции.
В отличие от классической математики, в задачах геопространственного анализа выделяют две группы методов: точная интерполяция, когда измерения функции в заданных точках считаются точными, и сглаживающая интерполяция для случаев, когда измерения выполнены с некоторой погрешностью.

Алгоритмы интерполяции могут использовать интерполяционные узлы по-разному. Если используются одновременно все точки, такие алгоритмы интерполяции называют глобальными. В локальных алгоритмах интерполяции используются узлы из некоторой окрестности точки, в которой рассчитывается значение функции.

Ниже приводятся методы, реализованные в инструментарии ArcMap, хотя на самом деле таких методов значительно больше. В пакете ArcMap также реализованы некоторые разновидности методов, подробное описание которых не удалось найти в доступной литературе, поэтому в данной работе мы ограничимся несколькими наиболее известными вариантами интерполяции. Другие методы, при желании, можно попробовать самостоятельно.
Методы точной интерполяции.
Метод естественной окрестности. Метод использует представление растровых данных в виде треугольных нерегулярных мозаик (TIN-модель растровых данных), а именно диаграмма Вороного (многоугольники, образованные серединными перпендикулярами к линиям, соединяющим интерполяционные узлы – эту конструкцию также называют триангуляцией Делоне). Сначала строится диаграмма Вороного для всех точек (x_i,y_i) окрестности точки (x₀,y₀), в которой должно быть рассчитано новое значение. Каждой точке (x_i,y_i), таким образом, сопоставляется многоугольник M(x_i,y_i). Затем в выборку добавляется сама точка (x₀,y₀) и строится новая диаграмма Вороного. Она накладывается на предыдущую, и пересечения многоугольника M(x₀,y₀) с многоугольниками M(x_i,y_i) дают «естественную окрестность» для (x₀,y₀), состоящую из точек (x_i,y_i), соответствующих этим многоугольникам. Оценка значения в точке (x₀,y₀) рассчитывается как средневзвешенное значение по точкам выборки, где веса точек определяются через доли площадей многоугольников, попавших в пересечение. Метод может работать как глобальный интерполятор и позволяет получать хорошие результаты при неравномерном пространственном размещении интерполяционных узлов.

Метод обратных взвешенных расстояний. Оценка значения в точке (x₀,y₀) рассчитывается по значениям точек z(x_i,y_i) из окрестности следующим образом: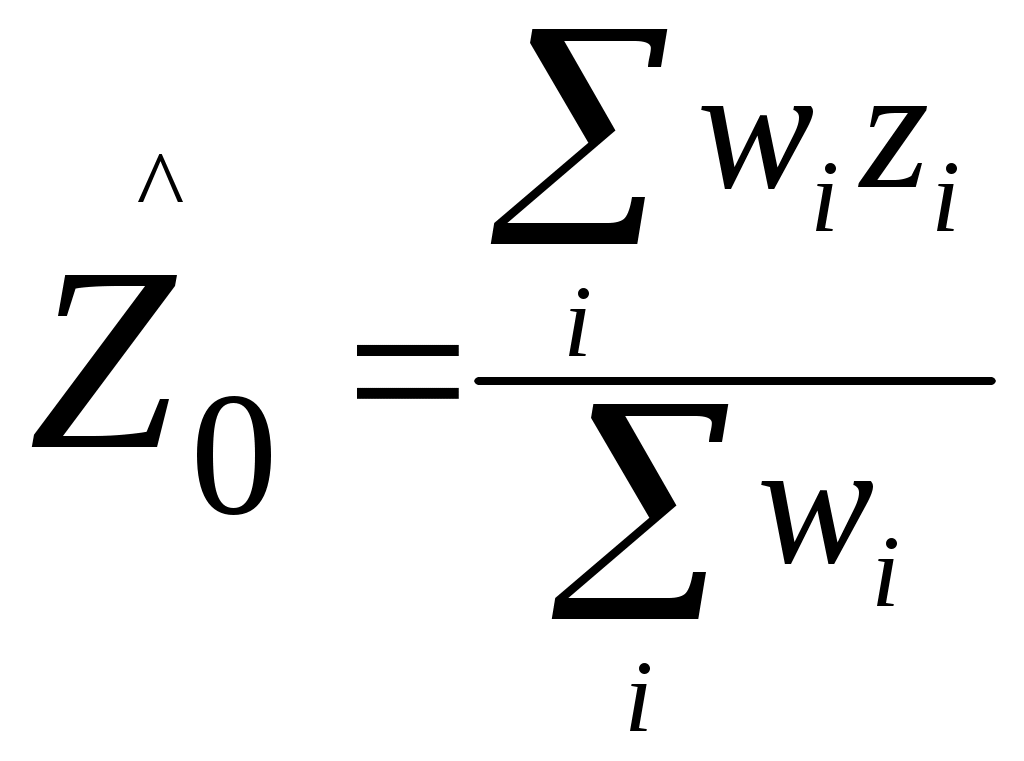

, .

Здесь d_0i – расстояние от (x₀,y₀) до (x_i,y_i),  - параметр сглаживания,  - степенной параметр, определяющий, как быстро будет убывать вес w_i с увеличением расстояния.

Метод предпочтительнее использовать как локальный интерполятор.

Полиномиальная интерполяция. В одномерном случае интерполяция алгебраическими многочленами (полиномами) предполагает решение системы уравнений вида

, i=0,1,…,n

Здесь неизвестными являются коэффициенты a_i. Определитель этой системы, известный как определитель Вандермонда, всегда отличен от нуля при попарно различных значениях x.

Очевидно, что для функции двух переменных сложность расчетов быстро растет с увеличением степени полинома, поэтому обычно для пространственной полиномиальной интерполяции используют полиномы не выше третьей степени. Метод может использоваться и как глобальный, и как локальный интерполятор.

Сплайн. Сплайном (алгебраическим) называется гладкая функция, «склеенная» из полиномов таким образом, чтобы в узлах состыковки выполнялось условие непрерывности их производных. Это условие можно обеспечить только для полиномов нечетной степени, поэтому на практике чаще всего пользуются кубическими сплайнами. Сплайн обычно используется как глобальный интерполятор. В ArcMap дополнительно может использоваться условие минимума кривизны двумерного сплайна.

Радиальные базисные функции. Оценка в точке x рассчитывается как

,

где B – базовая функция, h_i – расстояние от точки x до i-го интерполяционного узла,c_i – весовые коэффициенты.

Традиционно используются пять типов базисных функций:

-мультиквадрик ;

- обратный мультиквадрик ;

- мультилогарифмическая ;

- естественный кубический сплайн , ;

- тонкий сплайн .

Методы статистической (сглаживающей) интерполяции.
Инструменты точной интерполяции реализованы в модуле 3D Analyst пакета ArcMap и в основном используются для построения трехмерных моделей рельефа. Что же касается различных прикладных направлений использования инструментария ГИС, то здесь в основном приходится иметь дело с приближенными расчетами значений функций пространственных координат. Поэтому группа методов пространственной интерполяции для построения таких геопотенциалов находится в модуле Geostatistical Analyst. Но некоторые из методов присутствуют в обоих упомянутых модулях.

Если выражаться математически корректно, то группу методов сглаживающей интерполяции следует назвать аппроксимацией или обобщенной регрессией. То есть это методы построения тренда, наилучшим образом аппроксимирующего поведение «случайного поля» пространственных данных.

Полиномиальная регрессия. Глобальный интерполятор, в котором уравнение полинома строится по методу наименьших квадратов с использованием всех точек множества данных. В локальном интерполяторе полиномы строятся по локальной окрестности каждой точки, для которой выполняется оценка, со взвешенным вкладом точек, участвующих в процессе аппроксимации.

Кригинг (по имени применившего его впервые южноафриканского горного инженера Крига, известен также как метод Винера-Колмогорова). Кригинг является основой многих методов сглаживающей интерполяции.

В простейшем варианте кригинга оценка функции в точке вычисляется аналогично методу ОВР, однако веса рассчитываются по вариограмме – зависимости квадрата разности значений в точках от расстояния между ними. При этом вариограмма аппроксимируется функцией определенного типа. В так называемом «универсальном» кригинге дополнительно предполагается, что среднее значение m(x,y) плавно меняется во всей области исследования.

В ArcMap, кроме традиционной модели кригинга, имеется собственная разработка специалистов ESRI – эмпирический байесовский кригинг

Порядок выполнения работы.
Целью настоящей работы является общее знакомство с методами построения интерполяционных карт некоторых геопотенциалов на территорию Окского бассейна. В качестве исходных данных мы будем использовать данные по метеостанциям с центральной европейской части РФ (выборка из базы метеоданных NASA). Эти данные были собраны для моделирования биопотенциала природных экосистем Окского бассейна.

Загрузите в ArcMap карту-проект Ока-ArcMap.mxd из папки interpol. На карте представлена Ока с притоками и ее бассейн с границей. Метеостанции выбраны по расширенной территории, чтобы при интерполяции избежать неприятных «краевых эффектов». Сохраните этот проект сразу в собственной папке. Слои рек и озер можете отключить, они представлены только для ориентации на рабочей территории.

Из полного набора данных в этой таблице оставлены только высоты метеостанций над уровнем моря для моделирования рельефа и среднегодовая температура (результата расчета из данных по месяцам). Также оставлены расчетные данные по длительности вегетационного периода для хвойных лесов и средней температуре этого периода.

Методы точной интерполяции мы будем использовать для построения карты рельефа, методы статистической интерполяции – для построения карты среднегодовых температур. В данной работе заранее подобраны наиболее удачные параметры для используемых данных, но вообще в каждом отдельном случае методы и параметры нужно подбирать заново.

1. Построение карты рельефа.
В инструментарии ArcMap (кнопка ) из инструментов модуля 3D Analyst зайдите в группу Raster Interpolation. Для начала выберите метод Natural Neighbor (Естественная окрестность), не требующий настройки параметров. Выберите в окне функции поле ELEVATION и задайте файл на запись в собственной папке.

Программа сама выберет наиболее подходящее количество классов и цветовую шкалу для отображения результата, но для адекватного представления всех результатов интерполяции Вам придется отрегулировать интервалы классификации. Зайдите с правой кнопки в свойства созданного слоя и в закладке «Символы» нажмите кнопку «Классифицировать». Установите в правом нижнем окне граничные значения как показано на рис.1 слева. Нажмите ОК и в колонке «Надпись» полученной легенды наберите те же значения. Результат оформления легенды показан на рис.1 справа.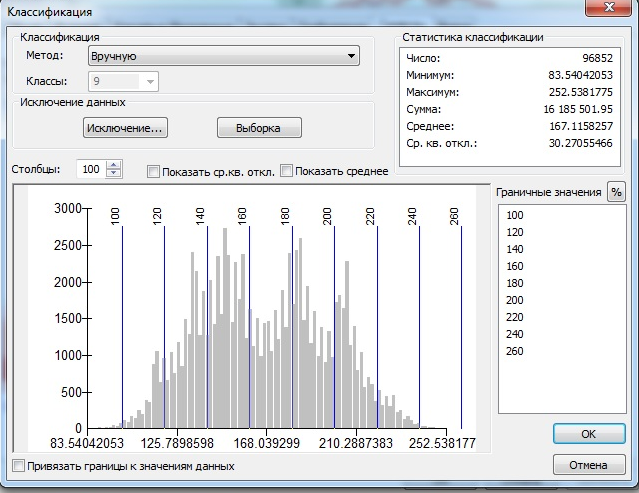


Рис.1.
В качестве второго метода, для сравнения результатов, используем обычный сплайн из той же группы инструментов. Для нашего типа данных пригоден только режим REGULARIZED, установленный по умолчанию. Вес третьей производной также менять не будем. Изменим только количество точек, участвующих в локальной интерполяции: с 12 на 8. Откройте файл на запись в своей папке и запустите процедуру. После ее выполнения установите легенду нового слоя так же, как и в предыдущем случае.

Вы, вероятно, обратили внимание, что контуры во втором случае получаются значительно более гладкие. Для этого растра мы можем построить изолинии, как показано на рис.2. Выберите функцию Contour в группе Raster Suface. Задайте в ней интервал между изолиниями 20 и базовое значение 100. Откройте файл на запись в собственной папке.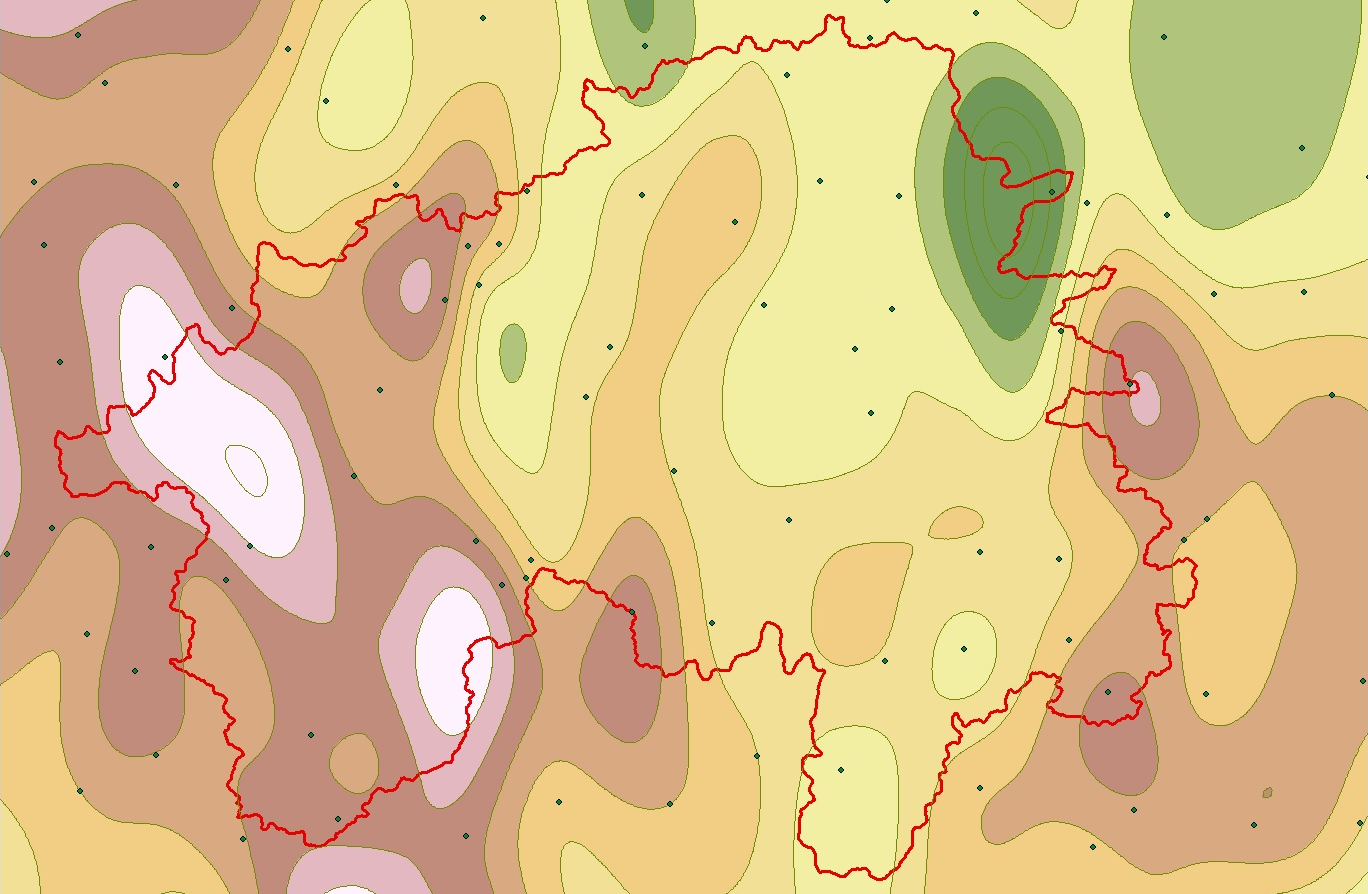

Рис.2.
Убедитесь, что полученный Вами результат соответствует показанному на рис,2.

Дополнительно можете самостоятельно попробовать метод обратных взвешенных расстояний (ОВР) и определить, в чем состоит его недостаток для наших данных.

Для выполнения следующего задания удалите созданные слои, предварительно показав их преподавателю (или сохраните результаты в виде отдельного проекта).

2. Построение карты среднегодовых температур.
Для построения карты среднегодовых температур будем использовать инструменты модуля Geostatistical Analysis. Откройте его инструментарий и в группе Interpolation для начала выберите интерполяцию по методу глобального полинома. Задайте поле значений MEAN_T, степень полинома 3 и файл на запись в своей папке. Полученный результат расклассифицируйте на 14 классов как показано на рис. 3.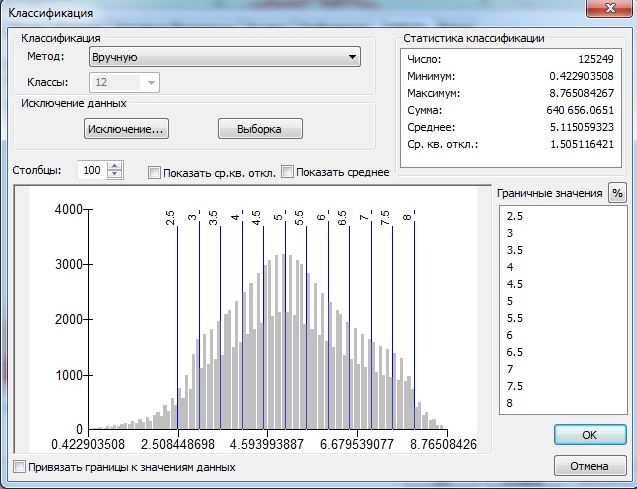

Рис.3.
Постройте для полученного растра изолинии, выбрав шаг 0.5 и базовое значение 5. Будем их использовать для сравнения с другими методами. Для удобства сравнения войдите в свойства слоя изолиний и в закладке надписи выберите поле надписи CONTOUR. Установите размер шрифта 12 или 14, чтобы Вы видели значения при подписывании.

Из других методов прежде всего попробуем интерполяцию по методу локальных полиномов. Чтобы обнаружить особенности этого метода достаточно запустить процедуру при параметрах по умолчанию. Вам нужно только установить поле значений MEAN_T и задать растр на запись результата в своей папке. Для полученного растра создайте легенду на 12 классов, чтобы цвета соответствовали нашему исходному результату.

Метод кригинга возьмем из интерполяционных инструментов модуля 3D Analyst (для наших данных подходит наиболее простой вариант). Вызовите эту функцию, установите поле значений MEAN_T, линейную модель вариограммы, число точек = 20 и задайте файл на запись нового растра в своей папке. По умолчанию в этот раз будет установлена другая шкала цветов, поэтому при создании легенды замените шкалу на идентичную предыдущим результатам по температуре. Расклассифицируйте результат на 12 классов, так же индентичных предыдущим вариантам.

Теперь повторите эту процедуру, переключившись с обычного кригинга на универсальный. Установите те же 20 точек и задайте файл на запись. Больше ничего не меняйте. Установите для результата такую же легенду, как в предыдущем случае.

Как Вы смогли убедиться, методы, использующие локальную окрестность, дают сильно различающиеся результаты. Чтобы посмотреть, насколько сильно зависит метод кригинга от числа точек в окрестности, выполним последнюю процедуру (универсальный кригинг) при числе точек = 60. Установите для него идентичную предыдущему случаю легенду и сравните результаты.

В заключение попробуем построить изолинии для одного из случаев, когда результат интерполяции недостаточно гладкий. В качестве исходных данных для такого случая используем результат интерполяции локальными полиномами. Сначала результат немного сгладим в растровом виде. Для этого используем функцию Focal Statistics из группы Neighborhood модуля Spatial Analyst. Установите в ней размер окна 5х5 и задайте файл на запись: по умолчанию там установлен простейший низкочастотный фильтр. Легенду для полученного результата не нужно классифицировать, можете только установить цветовую шкалу, аналогичную предыдущим результатам. Постройте для него изолинии так же, как и для метода глобального полинома.

Если в конкретном приложении нам не нужны детали интерполяции а требуется только «красиво» отобразить изолинии (например, те же изотермы), можно дополнительно сгладить последний результат. Зайдите в модуль Cartography Tools и там в группе Generalization выберите инструмент Smooth Line. Установите допуск сглаживания 50 км и выполните процедуру. Отключите предыдущий результат и убедитесь, что изолинии стали существенно более гладкими.