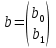Главная страница
Навигация по странице:

  • Лабораторная работа

  • 1 Анализ данных в Excel с использованием метода наименьших квадратов

  • 1.1 Решение 1

  • 1.2 Решение 2

  • 2 Реализация метода наименьших квадратов в MathCad

  • 3 Реализация метода наименьших квадратов в MATLAB

    		•

    Лабораторная Excel MathCad Matlab. Лабораторная работа Реализация метода наименьших квадратов с использованием различных программных пакетов Вариант 10 Тема (вариант) Преподаватель Т. В. Донцова Подпись, дата инициалы, фамилия


    Скачать 326.14 Kb.
    НазваниеЛабораторная работа Реализация метода наименьших квадратов с использованием различных программных пакетов Вариант 10 Тема (вариант) Преподаватель Т. В. Донцова Подпись, дата инициалы, фамилия
    Дата10.09.2018
    Размер326.14 Kb.
    Формат файлаdocx
    Имя файлаЛабораторная Excel MathCad Matlab.docx
    ТипЛабораторная работа
    #50201

    Федеральное государственное

    автономное образовательное учреждение

    высшего профессионального образования

    «СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»
    Институт цветных металлов и материаловедения
    Кафедра автоматизации производственных процессов в металлургии

    Лабораторная работа
    Реализация метода наименьших квадратов с использованием различных программных пакетов

    Вариант № 10

    Тема (вариант)


    Преподаватель ______________ Т. В. Донцова

    Подпись, дата инициалы, фамилия

    Студент ЦМ17-37М ______________ Г. А. Нестеров

    Код(номер) группы Подпись, дата инициалы, фамилия

    Красноярск 2018
    Задание в соответствии с вариантом работы:

    Определить зависимость механических свойств латуни ЛС59-1 от температуры отжига (58,5% Cu, 1,2% Pb, остальное Zn). Продолжительность отжига 1 ч. Исходный материал – прутки диаметром 5 мм, деформированные на 15%. Спрогнозировать предел прочности при растяжении в, кгс/мм2, при 800С. Построить квадратичную аппроксимирующую зависимость.

    Таблица 1 – Данные для решения задачи

    Предел прочности
    65
    64
    63
    61
    55
    52
    48
    47
    46
    46
    45
    44
    44

    Температура отжига, С
    0
    100
    200
    250
    300
    350
    400
    450
    500
    550
    600
    650
    700


    1 Анализ данных в Excel с использованием метода наименьших квадратов
    Для заданного набора значений независимой переменной и функции определить наилучшее линейное приближение в виде прямой с уравнением у=а·х+b.
    1.1 Решение 1

    – В программе Excel создана таблица заданных значений х и у (таблица 1);

    – в свободную ячейку в строке формул введена функция =ИНДЕКС(ЛИНЕЙН(значения x; значения y);1);

    – в следующей ячейке повторены операции, в итоге в этой ячейке появилась формула: =ИНДЕКС(ЛИНЕЙН(значения x; значения y);2).

    Теперь в этих ячейках вычислены соответственно коэффициенты а=-0,037и b=66,52 уравнения прямой.

    Сделана проверка графическим способом (рисунок 1): построен точечный график зависимости х и у, добавлена линейная линия тренда с выводом уравнения на диаграмме.
    Рисунок 1 – Проверка графическим способом

    1.2 Решение 2
    – меню Данные выбран Анализ данных. В открывшемся диалоговом окне выбрать пункт Регрессия;

    – введены входные интервалы Yи Х;

    В открывшемся рабочем листе Результат расчёта (рисунок 2) продемонстрированы результаты вычислений, в котором видно, что вычисленные коэффициенты совпали с полученными первым методом.


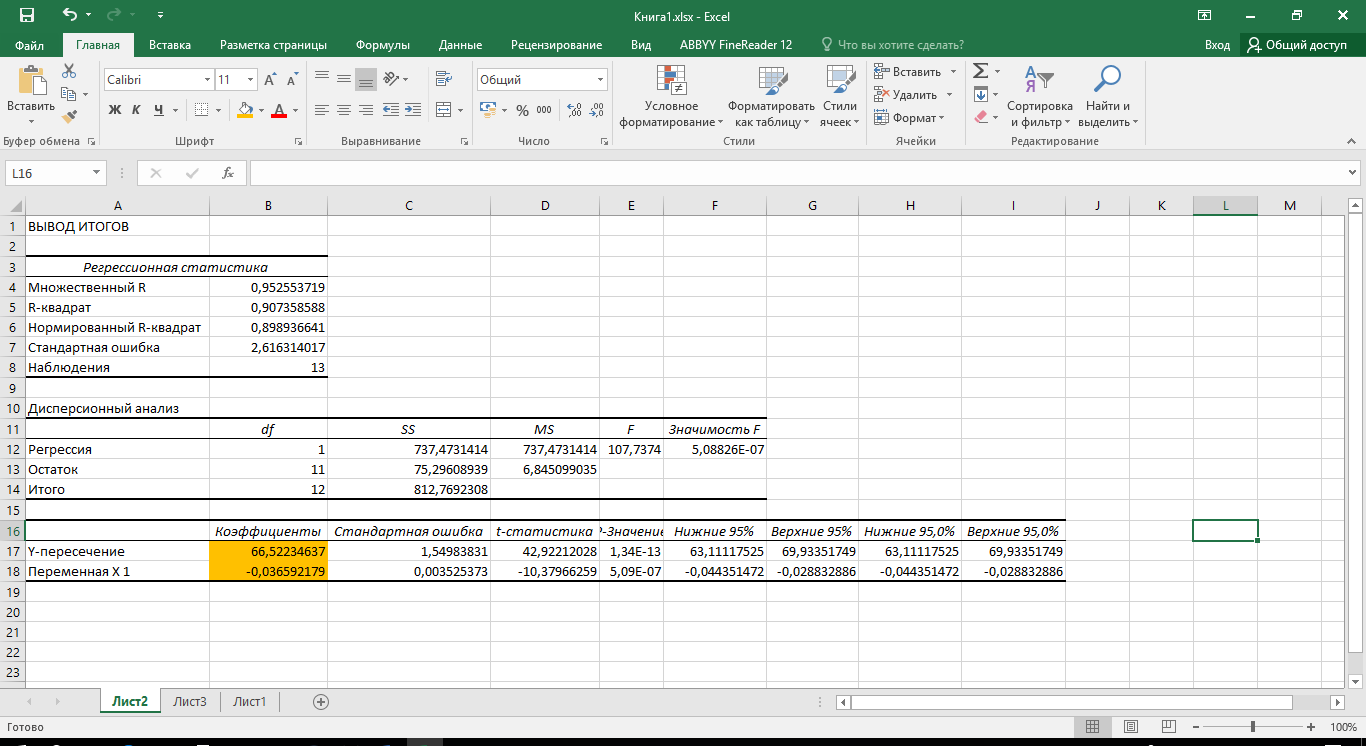
    Рисунок 2 – Расчет коэффициентов уравнения с помощью Анализа данных
    2 Реализация метода наименьших квадратов в MathCad
    Для определения коэффициентов регрессии b0, b1 в MathCad существуют следующие функции:

    • line(x, y) возвращает массив 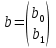коэффициентов регрессии;

    • intercept(x, y) возвращает коэффициент регрессии b0;

    • slope(x, y) коэффициент регрессии b1.

    Для вычисления коэффициента корреляции в MathCad предназначена функция corr(x, y).

    В этих функциях х – массив абсцисс экспериментальных точек, у – массив ординат экспериментальных точек.

    Результаты вычислений продемонстрированы на рисунке 3.


    Рисунок 3 – Построение линии регрессии и вычисление коэффициента корреляции
    С помощью функций regressиinterpможно подобрать коэффициенты полного полинома любой степени.

    Функция regress возвращает специальным образом сформированный массив, предназначенный для использования в функции interp, первые три элемента которого являются специальными значениями, используемыми функцией interp, а последующие элементы массива – коэффициентами подобранного полинома. Результаты вычислений продемонстрированы на рисунке 4.


    Рисунок 4 – Построение аппроксимирующих зависимостей
    3 Реализация метода наименьших квадратов в MATLAB
    Для подбора коэффициентов полинома k-ой степени методом наименьших квадратов в MATLAB есть функция polyfit(x,y,k) (х – массив абсцисс экспериментальных точек, у – массив ординат экспериментальных точек, k – степень полинома). Функция возвращает массив коэффициентов полинома.

    Затем можно вычислить значение полинома в любой точке с помощью функции polyval(k,t). В массиве kхранятся коэффициенты полинома, t – точка, в которой необходимо вычислить значение полинома. Эта функция вычисляет значение полинома в точке t по формуле k1tn+ k2tn-1+…+ knt+ kn+1.

    С помощью функций polyfitи polyval были подобраны зависимости y=a0+a1x+a2x2и y=b0+b1x+b2x2+b3x3. В нашем случае интересует полином второго порядка. Вычисление с помощью программного пакета MATLAB продемонстрированно на рисунке 5, график на рисунке 6.



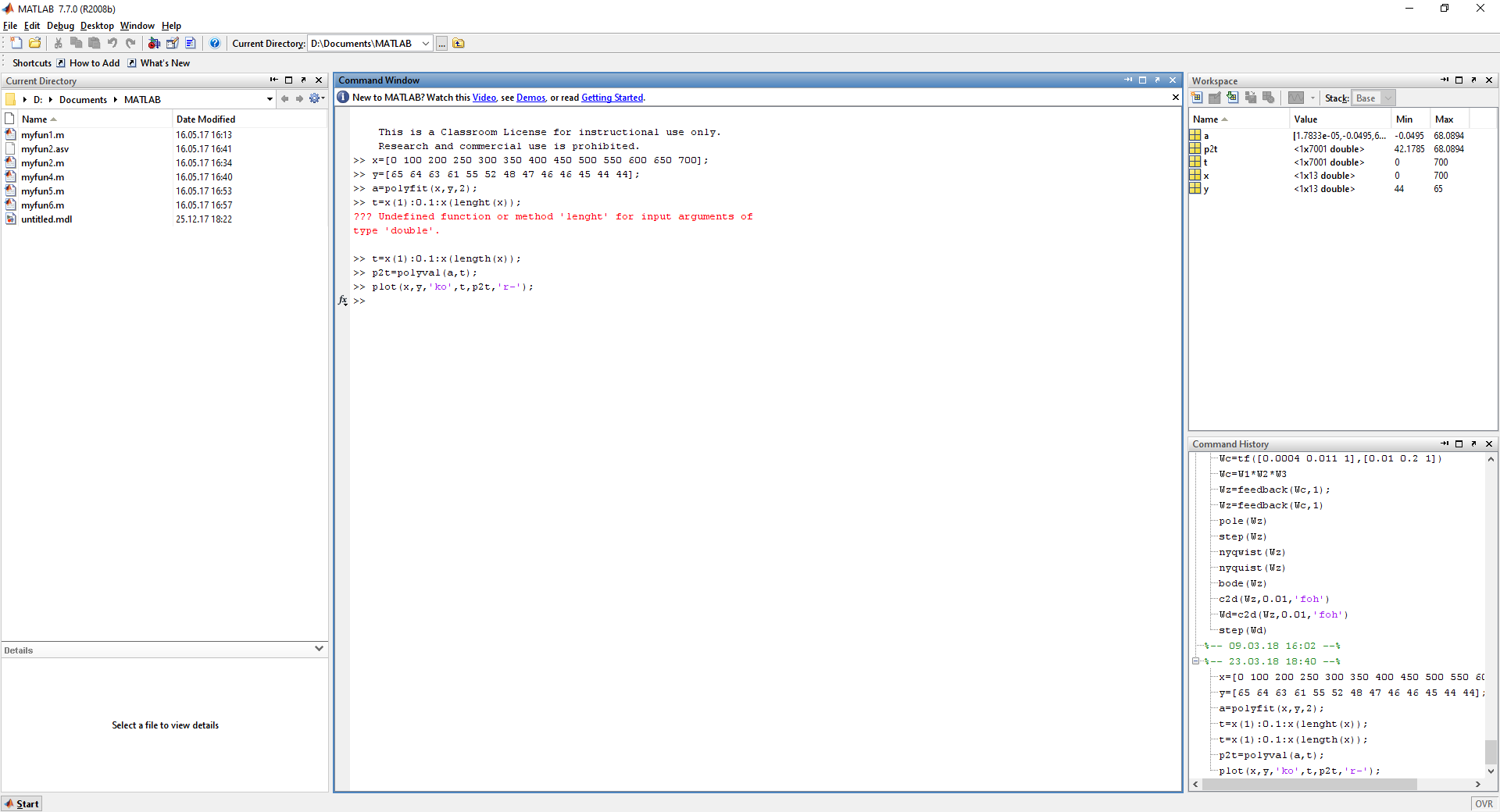
    Рисунок 5 – Листинг программы


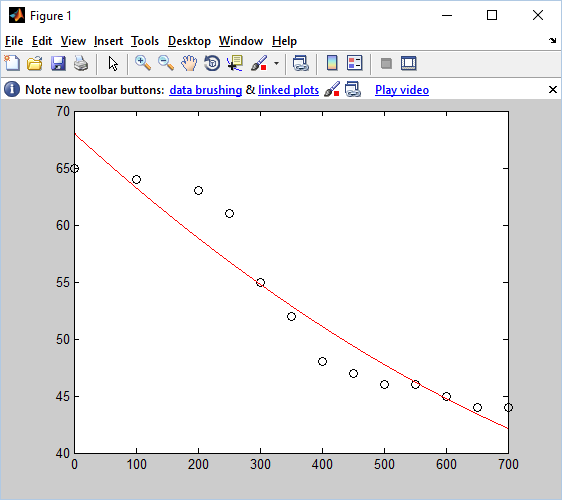
    Рисунок 6 – График подобранной зависимости

    Варианты заданий





    11
    Определить зависимость механических свойств латуни ЛН65-5 от степени деформации. Исходный материал – проволока мягкая диаметром от 0,25 мм и более. Спрогнозировать предел прочности при растяжении в, кгс/мм2, при 80% деформации. Построить кубическую аппроксимирующую зависимость.

    Предел прочности
    42
    45
    50
    55
    59
    62
    65
    69
    72
    75
    79
    82
    85
    87
    88

    Степень деформации, %
    0
    5
    10
    15
    20
    25
    30
    35
    40
    45
    50
    55
    60
    65
    70

    22
    Определить зависимость механических свойств латуни ЛН65-5 от степени деформации. Исходный материал – трубки манометрические с толщиной стенки 2 мм. Спрогнозировать относительное удлинение , % при растяжении в, кгс/мм2, при 70% деформации. Построить квадратичную аппроксимирующую зависимость.

    Относительное удлинение
    65
    55
    43
    35
    28
    20
    15
    12
    9
    7
    6
    5
    4
    4

    Степень деформации, %
    0
    5
    10
    15
    20
    25
    30
    35
    40
    45
    50
    55
    60
    65

    33
    Определить зависимость механических свойств латуни ЛН65-5 от степени деформации. Исходный материал – ленты мягкие толщиной 1,6 мм. Спрогнозировать предел прочности при растяжении в, кгс/мм2, при 75% деформации. Построить кубическую аппроксимирующую зависимость.

    Предел прочности
    30
    35
    37
    40
    43
    47
    49
    50
    52
    53
    55
    58
    59
    60

    Степень деформации, %
    0
    5
    10
    15
    20
    25
    30
    35
    40
    45
    50
    55
    60
    65

    44
    Определить зависимость механических свойств латуни ЛО90-1 от температуры отжига. Продолжительность отжига 1 ч. Исходный материал – полосы толщиной 3 мм, деформированные на 60%. Спрогнозировать относительное удлинение , % при растяжении в, кгс/мм2, при 800С. Аппроксимировать полиномом 4 степени.

    Относительное удлинение
    7
    7
    7
    10
    18
    35
    45
    55
    59
    57

    Температура отжига, С
    0
    100
    200
    300
    350
    400
    450
    500
    600
    700

    55
    Определить зависимость механических свойств латуни ЛО70-1 от температуры отжига. Продолжительность отжига 1 ч. Исходный материал – трубы конденсаторные, деформированные на 50%. Спрогнозировать предел прочности при растяжении в, кгс/мм2, при 700С. Аппроксимировать полиномом 5 степени.

    Предел прочности
    79
    80
    81
    78
    70
    50
    42
    40
    38
    36

    Температура отжига, С
    0
    100
    200
    250
    300
    350
    400
    450
    500
    600

    66
    Определить зависимость изменения механических свойств латуни ЛО70-1 при высоких температурах. Исходный материал – прутки диаметром 25 мм, деформированные на 35%. Спрогнозировать относительное удлинение , % при растяжении в, кгс/мм2, при 800С. Аппроксимировать полиномом 4 степени.

    Относительное удлинение
    12
    6
    8
    11
    15
    23
    36
    45
    32
    26

    Температура отжига, С
    150
    200
    250
    300
    350
    400
    450
    500
    600
    700




    77
    Определить зависимость изменения механических свойств латуни ЛО60-1 при высоких температурах. Спрогнозировать относительное удлинение , % при растяжении в, кгс/мм2, при 800С. Построить кубическую аппроксимирующую зависимость.

    Относительное удлинение
    21
    23
    25
    25
    24
    22
    20
    17
    12
    18
    25
    36

    Температура отжига, С
    50
    100
    200
    250
    300
    350
    400
    450
    500
    600
    650
    700

    88
    Определить зависимость изменения механических свойств латуни ЛО60-1 при высоких температурах. Спрогнозировать относительное удлинение , % при растяжении в, кгс/мм2, при 800С. Построить аппроксимирующую зависимость 4 порядка.

    Относительное удлинение
    33
    32
    25
    20
    11
    9
    16
    20
    22
    29
    30
    33

    Температура отжига, С
    50
    100
    200
    250
    300
    350
    400
    450
    500
    600
    650
    700

    99
    Определить зависимость изменения механических свойств латуни ЛО60-1 содержащей 0,4% Ni, при высоких температурах. Спрогнозировать относительное удлинение , % при растяжении в, кгс/мм2, при 800С. Построить аппроксимирующую зависимость 5 порядка.

    Относительное удлинение
    27
    29
    30
    32
    28
    26
    22
    21
    25
    35
    46
    52
    59

    Температура отжига, С
    50
    100
    200
    250
    300
    350
    400
    450
    500
    550
    600
    650
    700

    110
    Определить зависимость механических свойств латуни ЛС59-1 от температуры отжига (58,5% Cu, 1,2% Pb, остальное Zn). Продолжительность отжига 1 ч. Исходный материал – прутки диаметром 5 мм, деформированные на 15%. Спрогнозировать предел прочности при растяжении в, кгс/мм2, при 800С. Построить квадратичную аппроксимирующую зависимость.

    Предел прочности
    65
    64
    63
    61
    55
    52
    48
    47
    46
    46
    45
    44
    44

    Температура отжига, С
    0
    100
    200
    250
    300
    350
    400
    450
    500
    550
    600
    650
    700

    111
    Определить зависимость механических свойств литых оловянных бронз от содержания олова. Спрогнозировать предел прочности при растяжении в, кгс/мм2, при 15% Sn (по массе). Аппроксимировать полиномом 3 степени.

    Предел прочности
    21
    23
    28
    31
    37
    39
    38
    37
    37

    Sn, % (по массе)
    0
    2
    4
    6
    8
    10
    11
    12
    14

    112
    Определить зависимость механических свойств бронзы Бр.ОФ7,5-0,4 от температуры отжига. Продолжительность отжига 2 ч. Исходный материал – полосы, деформированные на 20%. Спрогнозировать относительное удлинение , % при растяжении в, кгс/мм2, при 750С. Аппроксимировать полиномом 2 степени.

    Относительное удлинение
    5
    5
    9
    20
    40
    55
    61
    69
    73
    79

    Температура отжига, С
    0
    100
    200
    300
    333
    366
    400
    500
    600
    700

    113
    Определить зависимость механических свойств латуни ЛС59-1 от температуры отжига (58,5% Cu, 1,2% Pb, остальное Zn). Продолжительность отжига 1 ч. Исходный материал – прутки диаметром 5 мм, деформированные на 15%. Спрогнозировать предел прочности при растяжении в, кгс/мм2, при 750С. Построить квадратичную аппроксимирующую зависимость.

    Предел прочности
    60
    62
    63
    61
    55
    52
    49
    47
    46
    45
    45
    44
    43

    Температура отжига, С
    0
    110
    210
    260
    310
    360
    400
    450
    500
    540
    600
    650
    700



    написать администратору сайта