|
|
Лабораторная Изучение последовательной RLC-цепи. Лабораторная работа Тема Изучение последовательной rlcцепи Цель Измерение параметров rlcцепи. Построение векторной диаграммы
Лабораторная работа
Тема: Изучение последовательной RLC-цепи
Цель: Измерение параметров RLC-цепи. Построение векторной диаграммы.
Оборудование: Источник питания 42В, резистор, катушка индуктивности, конденсатор, мультиметр, амперметр.
Краткая теория
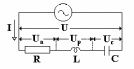 Рис. 1. Последовательное соединение R, L и C.
Наиболее общий случай неразветвленной цепи переменного тока представляет собой цепь, состоящая из последовательно соединённых участков с активным сопротивлением R, индуктивностью L и ёмкостью C (рис. 1). Приложенное к такой
цепи напряжение U составляется из трёх слагающих: активного напряжения Ua=IR, совпадающего по фазе с током I, индуктивного напряжения UL=IL, опережающего тока на 90, и емкостного напряжения 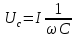 , отстающего от тока на 90 (рис. 2). , отстающего от тока на 90 (рис. 2).
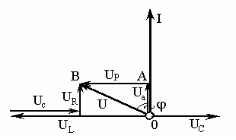
Рис. 2. Векторная диаграмма последовательного соединения.
Благодаря тому, что индуктивное и емкостное напряжения имеют противоположные фазы, их геометрическое сложение равносильно вычитанию соответствующих абсолютных величин. Если, например, индуктивное напряжение имеет большую абсолютную величину, чем емкостное, то результирующее реактивное напряжение опережает ток на 90:
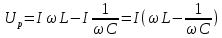 . .
Разностью 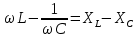 называется результирующим реактивным сопротивлением и обозначается буквой X: называется результирующим реактивным сопротивлением и обозначается буквой X:
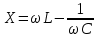 . .
Ёмкостное и индуктивное сопротивления можно рассматривать как частные случаи реактивного сопротивления, получаемые из этого общего выражения при отсутствии в цепи индуктивного (L=0) или емкостного 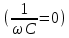 сопротивлений. В последнем случае, то есть при отсутствии в цепи конденсатора, следует считать, что С = . Действительно, для того, чтобы исключить конденсатор из цепи, нужно замкнуть накоротко его пластины, то есть сблизить их до соприкосновения, а известно, что при уменьшении расстояния между пластинами ёмкость конденсатора возрастает. сопротивлений. В последнем случае, то есть при отсутствии в цепи конденсатора, следует считать, что С = . Действительно, для того, чтобы исключить конденсатор из цепи, нужно замкнуть накоротко его пластины, то есть сблизить их до соприкосновения, а известно, что при уменьшении расстояния между пластинами ёмкость конденсатора возрастает.
При уменьшении емкости емкостное сопротивление возрастает и в пределе при С=0 становится бесконечно большим, так как в разомкнутой цепи ток не протекает. Если индуктивное сопротивление меньше емкостного или вовсе отсутствует, реактивное сопротивление становится отрицательным. Таким образом, обобщённое выражение результирующего реактивного сопротивления позволяет определять по знаку, является ли оно, в конечном счете, индуктивным или емкостным, то есть отстаёт по фазе ток в цепи от приложенного к ней напряжения или опережает напряжение.
Приложенное к цепи напряжение U представляется на векторной диаграмме (рис. 2) гипотенузой прямоугольного треугольника ОАВ и, следовательно,
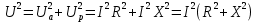 , ,
откуда
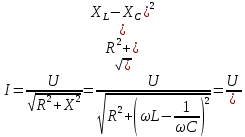 . (1) . (1)
Если в цепи имеется несколько активных, индуктивных и емкостных сопротивлений, то они группируются в соответствующие суммы и выражение закона Ома получает вид:
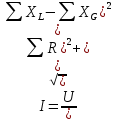 . .
Это – наиболее общее выражение закона Ома для неразветвлённой цепи переменного тока. Выражение (1) получается более компактным, если снова ввести полное сопротивление цепи:
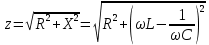 . .
Тогда закон Ома принимает знакомую форму:
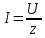 . .
Важно отметить следующее обстоятельство. С точки зрения расчёта тока в неразветвлённой цепи безразлично, в каком из её участков сосредоточена та или иная э.д.с.. Активное и реактивное напряжения могут как являются составляющими общего напряжения UL, так и могут иметь самостоятельное значение как напряжения между концами двух участков цепи.
Возможность отделения индуктивности какого-либо участка цепи от его активного сопротивления позволяет решить вопрос о расчёте тока при последовательном соединении нескольких приемников, каждый из которых обладает как активным сопротивлением, так и индуктивностью (например, трёх катушек рис. 3). В этом случае приложенное к цепи напряжение является геометрической
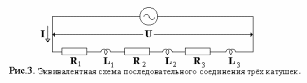
суммой всех активных напряжений, каждое из которых совпадает по фазе с током, и всех реактивных напряжений, каждое из которых опережает ток на 90. Поэтому суммарное активное напряжение будет равно арифметической сумме всех активных напряжений:
Ua=IR1+ IR2+ IR3+…=I(R1+R2+R3+…)=IR,
а суммарное реактивное напряжение арифметической сумме всех реактивных напряжений:
Uр=IXL1+ IXL2+ IXL3+…=I(XL1+XL2+XL3+…)=IXL,
которые тоже совпадают между собой по фазе.
Таким образом, активное сопротивление всей цепи R= R1+R2+R3+…
получается как сумма активных сопротивлений отдельных приемников, а индуктивное сопротивление всей цепи
XL= XL1+XL2+XL3+…
как сумма их индуктивных сопротивлений. Полное сопротивление всей цепи находится по уже известной формуле
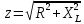
и применяется как для вычисления тока при заданном напряжении, так и для вычисления напряжения при заданном токе.
Таким образом, в общей форме закон Ома для последовательного соединения нескольких активных сопротивлений и индуктивностей может быть записан в виде формулы
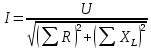 . .
Полезно заметить, что арифметическая сумма напряжений отдельных приемников может быть больше суммарного напряжения U. Это поясняет рис. 4, на котором представлена векторная диаграмма двух последовательно соединённых катушек. Напряжение U1 и U2 на зажимах каждой катушки получены путём геометрического сложения соответствующих активных (IR1и IR2) и реактивных (IL1 и IL2 ) слагающих.
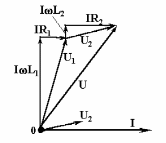
Рис. 4. Векторная диаграмма последовательного соединения катушек.
Выполнение работы
Изучив теорию, собрать цепь по схеме, рис. 5, где R и RL соответственно индуктивность и активное сопротивление катушки индуктивности.
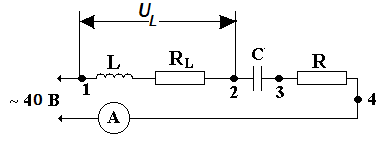
Рис. 5
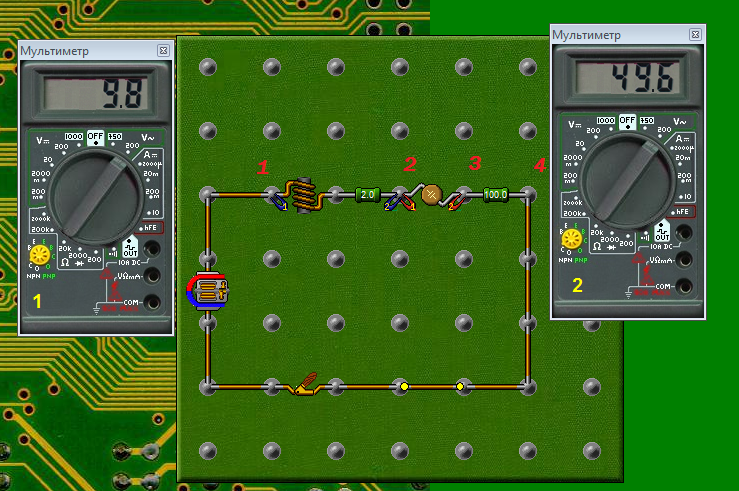
Рис. 6
2. Включив, после проверки преподавателем, схему в сеть 40В, измерить напряжение в сети U, на катушке UL, конденсаторе Uc и резисторе UR, подключив мультиметр, включённый на соответствующее положение, к нужным точкам. Так как в реальной катушке индуктивности невозможно физически отделить индуктивное XR и активноеRL сопротивление катушки, но мы можем измерить лишь общее напряжение на зажимах катушки UL между точками 1 и Записать измеренные напряжения в таблицу 1. Используя значение Rнайдите косвенным методом ток в неразветвленной RLC цепи и занесите в таблицу. Повторить измерения для других значений элементов цени.
таблица 1.
№
|
f, Гц
|
С,мкФ
|
XC, Ом
|
L,Гн
|
XL, Ом
|
R, Ом
|
UL,B
|
UC,B
|
UR,B
|
I,A
|
1
|
50
|
5
|
|
1
|
|
100
|
|
|
|
|
2
|
50
|
10
|
|
|
|
|
|
|
|
|
Отключив цепь от цепи, измерить активное сопротивление резистора R и катушки индуктивности RL. Зная индуктивность катушки L и её активное сопротивлениеRL, находим импеданс катушки для частоты =50 Гц
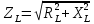
Найти сдвиг фазы между вектором тока в катушке I и напряжением UL:
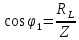 . .
Для значений 1-й строки таблицы построить топографическую векторную диаграмму цепи, аналогичную рис. 2, используя измеренные значения UL, cos1, UC, UK, U и I с учётом того, что XL диаграммы определить сдвиг фаз между током в цепи и напряжением на концах цепи. Обратить внимание на тот факт, что в реальной схеме элементы XL и RL не разделены.
На основании значений входного напряжения U, индуктивности L, активного сопротивления катушки XL, ёмкости конденсатора С, указанной на нём, и сопротивление резистора R рассчитать напряжения UL, UC, ток I и cos. Сравнить расчётные данные с измеренными. Сделать выводы.
Рассчитать на основе результатов опыта активную P, реактивнуюQ и полную Sмощность цепи.
Записать параметры приборов, используемых при измерениях.
Сделать выводы.
Контрольные вопросы
Объяснить методику построения векторной диаграммы для измеряемой цепи.
Каков физический смысл коэффициента мощности?
Чему равен сдвиг фаз между током в катушке и напряжением UL на ней?
|
|
|
 Скачать 0.59 Mb.
Скачать 0.59 Mb.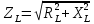
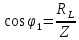 .
.

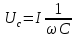 , отстающего от тока на 90 (рис. 2).
, отстающего от тока на 90 (рис. 2). 
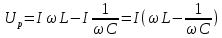 .
.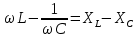 называется результирующим реактивным сопротивлением и обозначается буквой X:
называется результирующим реактивным сопротивлением и обозначается буквой X: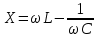 .
.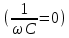 сопротивлений. В последнем случае, то есть при отсутствии в цепи конденсатора, следует считать, что С = . Действительно, для того, чтобы исключить конденсатор из цепи, нужно замкнуть накоротко его пластины, то есть сблизить их до соприкосновения, а известно, что при уменьшении расстояния между пластинами ёмкость конденсатора возрастает.
сопротивлений. В последнем случае, то есть при отсутствии в цепи конденсатора, следует считать, что С = . Действительно, для того, чтобы исключить конденсатор из цепи, нужно замкнуть накоротко его пластины, то есть сблизить их до соприкосновения, а известно, что при уменьшении расстояния между пластинами ёмкость конденсатора возрастает.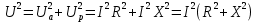 ,
,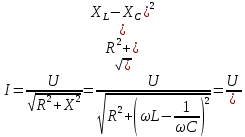 . (1)
. (1)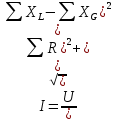 .
.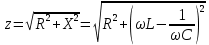 .
.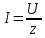 .
.
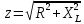
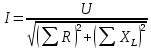 .
.

