ЛР Сапр методические реком. лаб работы САи ПР тех. Лабораторные

• Название: Лабораторные
• Анкор: ЛР Сапр методические реком
• Дата: 16.05.2022
• Размер: 167.64 Kb.
• Имя файла: лаб работы САи ПР тех.docx
• Тип: Реферат; #532655

СИСТЕМНЫЙ АНАЛИЗ

И ПРИНЯТИЕ РЕШЕНИЙ

Лабораторные работы

СОДЕРЖАНИЕ

Введение

Системный анализ — научный метод познания, представляющий собой последова- тельность действий по установлению структурных связей между переменными или посто- янными элементами исследуемой системы. В частности, системный анализ сигналов тех- нических систем позволяет установить особенности рабочих процессов.

Цифровая обработка сигналов, термин происходит от английского словосочетания DSP - digital signal processing, характеризует набор процедур по преобразованию исход- ных сигналов, как правило, полученных на приемнике по каналу передачи. Наиболее Рас- пространено представление сигнала в цифровой форме. Это справедливо, поскольку лю- бой непрерывный (аналоговый) сигнал может быть подвергнут дискретизации по времени и квантованию по уровню (оцифровке), то есть представлен в цифровой форме.

Если частота дискретизации сигнала не меньше, чем удвоенная наивысшая ча- стота в спектре сигнала (то есть ), то полученный дискретный сиг- нал эквивалентен сигналу , что полностью соответствует постулату – теореме Котельникова. При помощи математических алгоритмов преобразуется в некоторый другой сигнал имеющий требуемые свойства. Процесс преобразования сигналов называется фильтрацией, а устройство, выполняющее фильтрацию называется фильтром.

Поскольку отсчеты сигналов поступают с постоянной скоростью , фильтр дол- жен успевать обрабатывать текущий отсчет до поступления следующего отсчета. Такие устройства работают в реальном режиме времени, практически без задержки.

Для обработки сигналов, применяют специальные программы или программные модули, реализуемые как в специально создаваемых вычислительных средах, так и по- средством относительно несложных вычислительных процедур в среде типового офисно- го пакета Widows.

Данные представления позволяют, создавать вычислительные процедуры, приме- нительно не только к аналоговым, но цифровым сигналам. Различают методы обработки сигналов, как во временной, так и в частотной области. Эквивалентность частотно- временных преобразований однозначно определяется преобразованием Фурье.

В представленной подборке материалов по обработке сигналов выделены вопросы по формированию основных представлений по обработке сигналов. Следуя этим пред- ставлениям, в типовых задачах практикума предлагается найти решение, посредством об- работки исходного сигнала, указанными средствами и методами. Разработка процедур об- работки сигнала не требует обращения к специализированным пакетам анализа. Все про- цедуры по обработке сигнала – анализу, реализуются в типовой среде EXCEL, традицион- но встроенной в типовой пакет программ современного компьютера.

Принятие решений на основе проведенного анализа ответственная процедура, ко- торая должна формироваться на основе логически правильно выбранных критериев и чис- ленных показателей.

Часть 1 Исследование процессов фильтрации сигналов

Задача 1. Исследование амплитудного фильтра

Амплитуда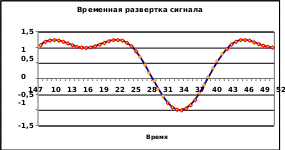
Имеется канал связи, передатчик и приемник сообщений, представленных времен- ной последовательностью амплитудных значений сигнала. Иллюстрация сигнала сообще- ния, посланного передатчиком на приемник, представлена на рис. 1.1.

Рис. 1.1 Форма сигнала принятого на приемнике
Известно:

1. передатчик формирует сигнал, описываемый выражением:


i i
x(t)  sin(t )  cos(t)²

Где:  =1

t₁  0,1,

2. t₂  0,25

t₃  0,4

и далее, при условии, что i=1,2,………,52, , а t=0,15 создать дискретный ряд амплитуд- ных значений сигнала.

Сигнал с передатчика по каналу связи поступает на приемник.

Задание 1.1
Используя типовой пакет Microsoft Office в среде Excel создать программный модуль вы- деления значений сигнала на приемнике, превышающих амплитудныйуровень 1,0.

Указание.

1. 
   При создании фильтра, выделяющего максимальные значения сигнала, использо- вать логическую процедуру «ЕСЛИ ………., ТОГДА » в среде Excel
   
2. 
   Результаты представить в среде Word с графическими пояснениями, исполненными в среде Excel.
   

Используя типовой пакет Microsoft Office в среде Excel создать программный модуль вы- деления отрицательных значений сигнала на приемнике.

Указание.

3. 
   При создании фильтра, выделяющего максимальные значения сигнала, использо- вать логическую процедуру «ЕСЛИ ………., ТОГДА » в среде Excel
   
4. 
   Результаты представить в среде Word с графическими пояснениями, исполненными в среде Excel.
   

Задача 2. Исследование полосового амплитудного фильтра

Амплитуда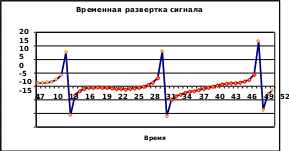
Имеется канал связи, передатчик и приемник сообщений, представленных времен- ной последовательностью амплитудных значений сигнала. Иллюстрация сигнала сообще- ния, посланного передатчиком на приемник, представлена на рис. 2.1.

Рис. 2.1 Форма сигнала принятого на приемнике
Известно:

1. передатчик формирует сигнал, описываемый выражением:

i
x(t)  sin(t

)³  cos(t)⁵  (

sin(t_i ) ₎

i
Где:  =1

t₁  0,1,

ⁱcos(t

  )

2. t₂  0,25

t₃  0,4

3.  =0,5

и далее, при условии, что i=1,2,………,52, , а t=0,15 создать дискретный ряд амплитуд- ных значений сигнала.

Сигнал с передатчика по каналу связи поступает на приемник.

Задание 2.1
Используя типовой пакет Microsoft Office в среде Excel создать программный модуль вы-

деления значений сигнала на приемнике, а диапазоне Указание.

 5 

x(t)  -5

1. 
   При создании фильтра, использовать логическую процедуру «ЕСЛИ , ТО-
   

ГДА » в среде Excel

2. 
   Результаты представить в среде Word с графическими пояснениями, исполненными в среде Excel.
   

Задание 2.2

Используя типовой пакет Microsoft Office в среде Excel создать программный модуль вы-

деления значений сигнала на приемнике, а диапазоне Указание.

 0  x(t)  12,0

3. 
   При создании фильтра, использовать логическую процедуру «ЕСЛИ , ТО-
   

ГДА » в среде Excel

4. 
   Результаты представить в среде Word с графическими пояснениями, исполненными в среде Excel.
   

Задача 3. Исследование амплитудного детектора

Амплитуда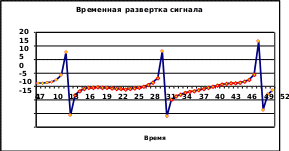
Имеется канал связи, передатчик и приемник сообщений, представленных времен- ной последовательностью амплитудных значений сигнала. Иллюстрация сигнала сообще- ния, посланного передатчиком на приемник, представлена на рис. 3.1.

Рис. 3.1 Форма сигнала принятого на приемнике
Известно:

1. передатчик формирует сигнал, описываемый выражением:

x(t)  sin(t

i
)³  cos(t)⁵  (

sin(t_i ) ₎

i
Где:  =1

t₁  0,1,

ⁱcos(t

  )

2. t₂  0,27

t₃  0,44

3.  =0,5

и далее, при условии, что i=1,2,………,52, а t=0,17 создать дискретный ряд амплитудных значений сигнала.

Сигнал с передатчика по каналу связи поступает на приемник.
Задание 3.1
Используя типовой пакет Microsoft Office в среде Excel создать программный модуль вы- деления максимальных значений сигнала на приемнике, а диапазоне

 2,0  x(t)  -2,0

По умолчанию полагаем, что в указанном диапазоне амплитудные значения сигна-ла могут принимать любые значения, как положительные, так и отрицательные, но поусловиюзадачиследуетвыделитьмаксимальныеположительныезначения.Другимисло-вами, внутри указанного интервала требуется выделить максимальные амплитудныезначения сигнала, которые могут быть зафиксированы приемником, в самом общем слу-чае, в любой произвольный момент времени. Иллюстрация на рис. 3.1 к этому заданиюпозволяетвизуальноустановитьналичиетакогоамплитудногопика,важносоздать

формализованное правило в среде Excel, обеспечивающее амплитудную селекцию значенийсигнала.
Указание.

1. 
   При создании фильтра – детектора , использовать логическую процедуру «ЕСЛИ
   

………., ТОГДА » в среде Excel

2. 
   Результаты представить в среде Word с графическими пояснениями, исполненными в среде Excel.
   

Задание 3.2

Используя типовой пакет Microsoft Office в среде Excel создать программный модуль вы- деления значений сигнала на приемнике, а диапазоне

 5,0  x(t)  -5,0

Указание.

3. 
   При создании фильтра - детектора, использовать логическую процедуру «ЕСЛИ
   

………., ТОГДА » в среде Excel

4. 
   Результаты представить в среде Word с графическими пояснениями, исполненными в среде Excel.
   
5. 
   Проиллюстрировать полученные результаты. Сопоставить результаты исполнения заданий 3.1 и 3.2, сделать выводы
   

Часть 2 Точечные оценки исследуемого процесса

Рассмотрим некоторый процесс, например, передачу сообщения, представленного набором амплитудных значений сигнала. Поскольку каждое сообщение конечно, то сле- довательно количество содержащихся в сообщении амплитудных значений ограничено. Назовем такую реализацию выборкой. Рассмотрим оценки выборки.

Точечной называют статистическую оценку, которая определяется одним числом.

Несмещенной называют точечную оценку, математическое ожидание которой равно оце- ниваемому параметру при любом объеме выборки.

Смещенной называют точечную оценку, математическое ожидание которой не равно оцениваемому параметру.

Несмещенной оценкой генеральной средней (математического ожидания) служит выборочная средняя, определяемая по выражению:


k

1
_- ^{ n}i^xi

_xвi1

n

k

^{где x}i ^{варианта выборки; n}i ^{частота встречаемости варианты x}i ^{в выборке, и количество} значений (вариант) в выборке определяется выражением:

n _n_i


2
i1
Смещенной оценкой генеральной дисперсии служит выборочная средняя, определяемая по выражению:

^k  ³

_ n_i(x_i x_в)

2

_n x²

_ nx

_{D }i1 _

в _n

i i _[


n

i i_]2

n

Несмещенной оценкой генеральной дисперсии служит исправленная выборочная диспер- сия, определяемая по выражению:


k

k

k

i

i



4
[_ nx]²

_n (x

 x)²

_{ nx}² _i1

_n i i в i i _n

s² 

_{D }i1 _i1

n 1 ^в

n -1

n 1

Задача 4. Формирование оценки выборки сигнала

В десяти независимых измерениях температуры процессора, установленного на компьютере, получены следующие значения:

Таблица 4.1

Температурные значения процессо- ра Тi	38.6	48.2	45.3
ni	2	5	3
n	10

Задание 4.1

Вычислить значение выборочной дисперсии по данному распределению выборки (таблица 4.1).

Вычислить значение выборочной дисперсии по данному распределению выборки по сле- дующим данным - таблица 4.2.
Таблица 4.2

Температурные значения процессо- ра Тi	31,1	28,6	27,2
ni	3	4	3
n	10

Указание

Воспользоваться формулой (3). Дать пояснения полученным результатам
Задание 4.2

Вычислить значение исправленной выборочной дисперсии по данному распределению выборки: таблица 4.1 и таблица 4.2.

Указание

Воспользоваться формулой (4). Дать пояснения полученным результатам Оформить отчет по заданию

Задача 5. Формирование оценки коррелированности сигналов

На приемник поступают два сообщения – два сигнала, описываемые выражениями (5.1) и (5.2). Требуется установить степень тождественности – схожести сигналов. С этой целью проводится вычисление корреляционной функции.

Корреляция — статистическая взаимосвязь двух или нескольких случайных вели- чин, составляющих выборку. Математической мерой корреляции двух случайных величин служит коэффициент корреляции.

Коэффициент корреляции обозначается латинской буквой R и может принимать значения от −1 до +1. Если значение R по модулю находится ближе к 1, то это означает наличие сильной связи, а если ближе к 0 — связь слабая или вообще отсутствует. При ко- эффициенте корреляции равном по модулю единице говорят о функциональной связи, то есть изменения двух величин можно описать математической функцией.

Задание 5.1

Вычислить значение коэффициента корреляции для выборочных значений двух сигналов, заданных выражениями:

x (t)  A

• 
  sin( t
  

)³  cos( t)⁵  (

sin(₁t_i ) ₎

5.1.1

1 i
1 1 1 i

cos(₁t_i

 ₂ )

^{При условии: А}1^{= 0 ; }1 ^{= 480 ; i= 1,2,3,……. ,52; }1 ^{= 0}

x (t)  A  sin( t )³  cos( t)⁵  (

sin(₂t_i ) ₎

5.1.2

2 i
2 2 2 i

cos(₂t_i₂ )

^{При условии: А}2^{= 50 ; }2 ^{= 240,260,280, ……520 ; i= 1,2,3,……. ,52; }2 ^{= 0}
Создать иллюстративный материал в среде EXCEL , поясняющий результаты расчетов. Оформить отчет по заданию.
Задание 5.2

Вычислить значение коэффициента корреляции для выборочных значений двух сигналов, заданных выражениями:

x (t)  A

• 
  sin( t
  

)³  cos( t)⁵  (

sin(₁t_i ) ₎

5.2.1

1 i
1 1 1 i

cos(₁t_i

 ₂ )

^{При условии: А}1^{= 0 ; }1 ^{= 480 ; i= 1,2,3,……. ,52; }1 ^{= 0}

x (t)  A  sin( t )³  cos( t)⁵  (

sin(₂t_i ) ₎

5.2.2

2 i
2 2 2 i

cos(₂t_i₂ )

^{При условии: А}2^{= 50 ; }2 ^{=480; i= 1,2,3,……. ,52; }2 ^{= 0,25;0.5;0.75;……;4.0}
Создать иллюстративный материал в среде EXCEL , поясняющий результаты расчетов. Указание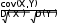

Вычисления коэффициента корреляции провести по выражению:

R(X, Y) 


N

Где:
_[( x_i x_в)(y_i  y_в)

cov( X,Y) ^i1

N -1

_(x_i x_в)



2

2
_( y_i y_в)

D( X) 

i1

N 1

D(Y) 

i1

N1

Создать иллюстративный материал в среде EXCEL , поясняющий результаты расчетов. Оформить отчет по заданию

Заключение

Анализ сигналов представляется актуальной задачей, рассматриваемой при реше- нии большого количества проблем в области создания и эксплуатации технических и эр- гатических систем. Под эрратической системой понимаем сложную техническую систему, в которой предусматривается деятельность человека. Принимая во внимание, что все со- временные сложные системы содержат элементы микропроцессоров – вычислительных модулей, возникает необходимость обработки большого количества сигналов и представ- ления их в той форме, которая наиболее полно и всесторонне отражает существо контро- лируемого или исследуемого процесса. Так, например, в технической системе «автопи- лот» происходит выделение цели, посредством обработки множества входных сигналов, а в технической системе тестирования большого тиража микросхем – отбор дефектных из- делий. И в том и другом случае, безусловно, требуется участие человека, задающего ис- ходные правила выбора правильного решения задачи и, одновременно с этим, предлага- ющим эффективные средства по достижению указанной цели.

Исполненные работы практикума способствуют закреплению основных понятий работы с аналоговыми и цифровыми сигналами. Полученные результаты практических заданий, требуют определенных знаний, чтобы сформулировать выводы, которые можно отыскать в литературе, в том числе и лекционном курсе по этой дисциплине.

Литература

1. 
   Афонский А. А., Дьяконов В. П. Цифровые анализаторы спектра, сигналов и логи- ки СОЛОН-Пресс, 2007
   
2. 
   Макаров Л.М. Курс лекций «Методы обработки сигналов» СПбГУТ 2009
   
3. 
   Оппенгейм А., Шафер Р. Цифровая обработка сигналов Техносфера, 2007