Теория массового обслуживания. лабораторная 1. Лабораторной работы 1

• Название: Лабораторной работы 1
• Анкор: Теория массового обслуживания
• Дата: 07.03.2022
• Размер: 177 Kb.
• Имя файла: лабораторная 1.doc
• Тип: Закон; #385467

Заданиелабораторной работы №1
1. Выполните имитацию работы банка, осуществляющего прием вкладов. Размер депозита является случайной величиной с нормальным законом распределения (среднее значение - МD; среднее квадратическое отклонение - SD). Время между приходом двух вкладчиков – случайная величина с показательным законом распределения (среднее значение - tz), а время обслуживания равномерно распределено на интервале [ a;b]. Пусть исходные значения равны величинам: MD=30000 руб.; SD=10000 руб.; tz=1 час (перевести в минуты) ;a=20 мин.; b=30 мин.; tn=9 ч., число заявок равно 5. Определите время прихода последнего клиента, среднее время пребывания клиента в системе. Какой общий размер вкладов будет осуществлен а) после прихода пяти клиентов; б) к моменту времени 12:00 ч.?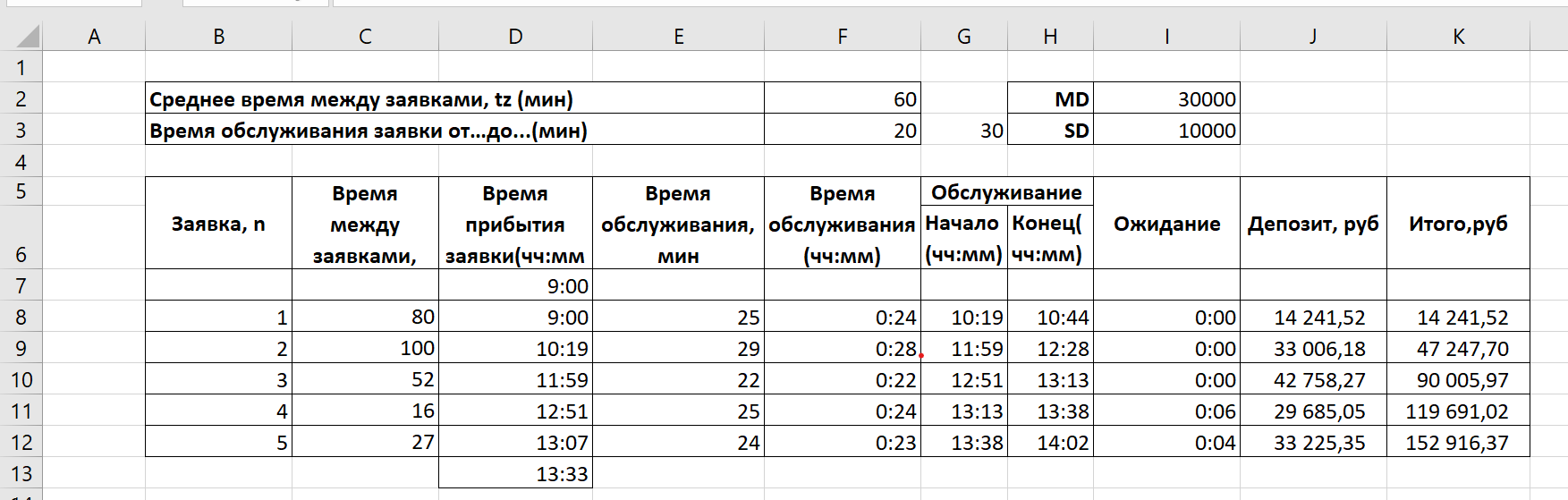




2. Проведите 10 экспериментов и рассчитайте величины:
 среднее время ожидания;
 среднее число обслуженных заявок за период с 9:00 до 15:00 ч.

3. Предположите, что tn=0 и выполните имитацию описанным на рис. Способом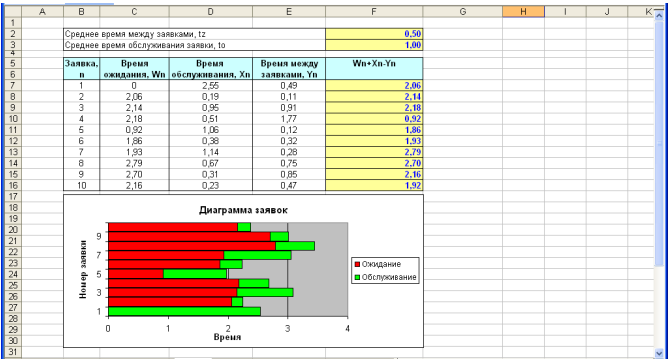




Пример смотри в лекции: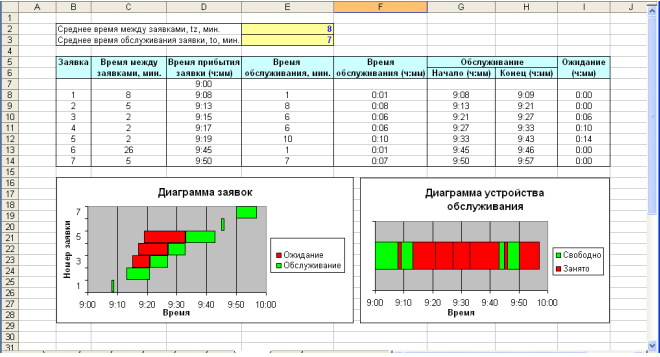