Измерение линейных размеров контактным и бесконтактным методами. лб. Лабороторная работа
 Скачать 175.03 Kb. Скачать 175.03 Kb.
|
|
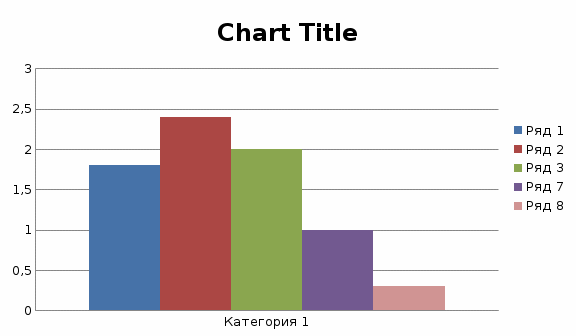
ЛАБОРОТОРНАЯ РАБОТА «Измерение линейных размеров контактным и бесконтактным методами» Цели работы: • получение практических навыков измерения линейных размеров ультразвуковым дальномером Bosch DUS 20 plus и рулеткой. • приобретение навыков обработки результатов многократных неравноточных измерений. Устройство и принцип работы ультразвукового дальномера Bosch DUS 20 plus*1 Принцип работы прибора (рис. 1.1) основан на акустическом отражении ультразвуковой волны от плоской преграды.  Элементы прибора: Элементы прибора:‒ жидкокристаллический дисплей; ‒ кнопка «измерительная функция» (длина, площадь, объем); ‒ кнопка «измерение»; ‒ кнопка «включение-выключение» (on/of); ‒ кнопка «вызов из памяти» (MR); ‒ кнопка «суммирование в памяти» (М+); ‒ кнопка «сброс» (С/МС); ‒ отверстие для выхода ультразвукового излучения; ‒ отверстие для выхода лазерного излучения; ‒ крышка батарейного отсека. Основные характеристики дальномера Диапазон измерений 0,6 ‒ 20 м. Точность измерений (+10 ‒ +40 °С) ± 0,5 % (‒5 ‒ +50 °С) ± 1 %. Рабочий диапазон температур ‒5 ‒ +50 °С. Диапазон температур хранения ‒20 ‒ +85°С. Краткие теоретические сведения Контактный метод измерений основан на том, что чувствительный элемент прибора приводится в контакт с объектом измерения (измерение температуры тела термометром, измерение линейных размеров). Бесконтактный метод измерений основан на том, что чувствительный элемент прибора не приводится в контакт с объектом измерения (измерение расстояния до объекта радиолокатором, измерение температуры в доменной печи пирометром). Погрешности измерений. По характеру проявления погрешности измерений можно разделить на систематические, случайные и грубые (промахи). Систематические погрешности постоянны по величине и по знаку или изменяются по определенному закону в зависимости от характера неслучайных факторов, их вызвавших. Постоянные систематические погрешности являются следствием неточной настройки средств измерений или условий измерения. Во многих случаях систематические погрешности могут быть сведены к нулю за счет тщательной организации и планирования измерений. Случайные погрешности ‒ это результат влияния случайных факторов, непостоянны по величине и знаку, непредсказуемы. Однако на основании предыдущих данных с помощью теории вероятности и математической статистики можно оценить пределы, в которых изменяется значение случайной суммарной погрешности. Грубые погрешности считаются следствием недосмотра. Они подлежат выявлению и исключению до обработки результатов измерений. В данной лабораторной работе влияние грубых погрешностей не учитывается. Вероятность проявления случайной величины. Действительный размер, полученный путем измерений, является случайной величиной. Обработку результатов измерений часто проводят с применением методов теории вероятностей и математической статистики. Отношение числа п случаев проявления события А к числу N произведенных испытаний, при котором это событие могло проявиться, называют частостью W события А. Если число измерений N достаточно большое, то частость проявления события становится устойчивой, и значение W(A) будет колебаться около некоторого постоянного числа. Это число является вероятностью Р проявления события А ( ) ( ) . N n P A ≈W A = Законы распределения случайных величин. Результаты измерений ‒ есть случайные величины, характеризующиеся законами распределения (функцией плотности распределения вероятности). Плотность распределения вероятности Р(Х) является пределом отношения приращения вероятности попадания случайной величины X в некоторый интервал к величине этого интервала при его неограниченном уменьшении. Характеристиками случайных величин следует полагать также математическое ожидание (или центр распределения) а и дисперсию D. Величина а характеризует среднее значение, a D ‒ разброс случайного значения. Величину σ = D называют средним квадратичным отклонением (СКО). Из числа теоретических законов распределения случайной величины наиболее часто встречается закон нормального распределения (закон Гаусса). Известно, что данному закону подчиняются случайные величины, на которые оказывает влияние большое число факторов, причем каждый из них не является доминирующим и играет малую роль в общей совокупности. Для определения характера распределения случайной величины строят гистограмму ее опытного распределения (рис. 1.2). Сначала определяют размах рассеяния результатов измерений (разность максимального и минимального значений в ряду измерений). Размах делится на равные интервалы. Определяют границы интервалов, их середину (X̅i), количество результатов измерений, попавших в каждый интервал (частота проявления ni), и частость проявления – отношение частоты проявления к общему числу измерений (ni /N). По оси абсцисс откладывают интервалы действительных размеров в миллиметрах, а по оси ординат ‒ частость проявления величины (ni /N). Ломаная линия, соединяющая середины полос гистограммы, называется полигоном распределения. 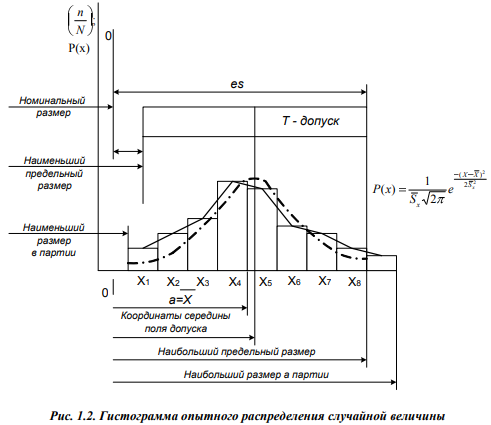 Кривые нормального распределения описываются уравнением: 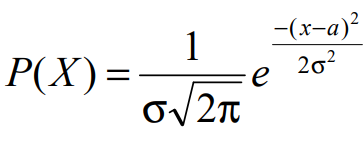 где Р(Х) ‒ плотность распределения вероятности случайной величины х; а ‒ центр группирования, определяемый математическим ожиданием; σ ‒ среднее квадратическое отклонение (СКО); X ‒ аргумент функции плотности вероятности. На практике мы имеем дело с конечным числом измерений в серии, поэтому для математической обработки результатов измерений используются точечные оценки a ≈ X и σ ≈ Sx : 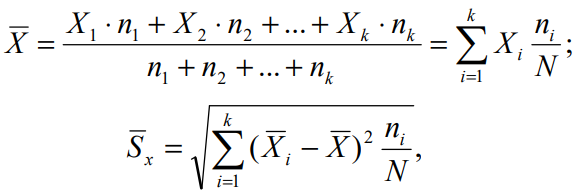 где k ‒ число равных интервалов, на которые делится размах (Хmax ‒ Хmin) действительных размеров в ряду (серии) измерений (рекомендуется принимать k = 8 ‒ 15); X i ‒ значение, соответствующее середине i-гo интервала; N ‒ общее число измерений (число измерений в серии). Полученное на основе экспериментальных данных значение x S позволяет определить наибольшее рассеяние случайной величины. Для закона нормального распределения граница поля рассеяния 99,73 % объекта измерений лежит в пределах x ± 3⋅ S . Чем меньше расчетное значение x S , тем выше действительная точность объекта измерений. Решение Результаты многократных измерений объёма помещения, полученные с помощью дальномера.
Результаты многократных измерений линейных размеров и косвенного измерения объёма помещения, полученные с помощью рулетки.
X max=147,65. X min=144,08. 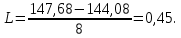
 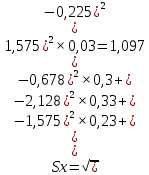 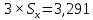 Вычисляют среднее арифметическое значение измерений объёма помещения: 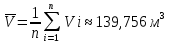 Находим среднее квадратическое отклонение: 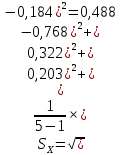 Рассчитывают предельные значения абсолютных погрешностей измерений: 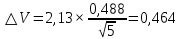 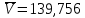 и определяют границы доверительного интервала: 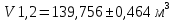 За результат неравноточных многократных измерений принимают среднее взвешенное или весовое среднее. Средневзвешенную величину объёма помещения рассчитывают по формуле: 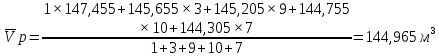 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

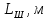
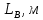
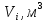
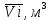
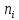
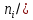 N
N