математика. Математика. Практическая работа. Лапшакова А.Б.. Лапшакова Алена Брониславовна
 Скачать 29.34 Kb. Скачать 29.34 Kb.
|
Практическое задание
дисциплине
Пермь 20___ Задание 1. Решить систему линейных алгебраических уравнений x+2y-z=2 2x-3y+2z=2 3x+y+z=8 Решение: Умножим первое уравнение на 2. Получим СЛАУ: 2x+4y-2z=4 2x-3y+2z=2 3x+y+z=8 Вычтем из первого уравнения второе. Получим СЛАУ: 7y-4z=2 3x+y+z=8 Преобразуем первое уравнение. Получим СЛАУ: y=(2+4z)/7 3x+y+z=8 Подставим y во второе уравнение. Получим уравнение: 3x+(2+4z)/7+z=8 3x+2/7+4z/7+z=8 3x+2/7+11z/7=8 3x=8-2/7-11z/7 3x=54/7-11z/7 x=18/7-11z/21 Подставим x в первое уравнение исходной СЛАУ. Получим уравнение: 18/7-11z/21+2y-z=2 2y=2-18/7+11z/21+z 2y=-4/7+32z/21 y=-2/7+16z/21 Подставим x и y в третье уравнение исходной СЛАУ. Получим уравнение: 54/7-11z/7-2/7+16z/21+z=8 -11z/7+16z/21+z=8-54/7+2/7 4z/21=4/7 z=3 Подставим значение z в уравнение для вычисления x: x=18/7-11z/21 x=18/7-11*3/21 x=1 Подставим значение z в уравнение для вычисления y: y=-2/7+16z/21 y=-2/7+16*3/21 y=2 Получаем: x=1, y=2, z=3. Проверка: подставим значения x,y,z в первое уравнение исходной СЛАУ: x+2y-z=2 1+2*2-3=2 2=2 Ответ: x=1, y=2, z=3. Задание 2. Дано z1 = 5 – 4i и z2 = –1 – i. Выполнить действия: А) z1+ z2; Б) z1 × z2; В) z1 / z2. Решение: А) z1+ z2 = 5-4i-1-i = 4-5i Б) z1 × z2 = (5-4i)*(-1-i) = -5+4i-5i+4i2 = -5-i+4*(-1) = -9-i В) z1 / z2 = (5-4i)/(-1-i) = (5-4i)*(-1+i)/((-1-i)*(-1+i)) = (-5+4i+5i-4i2)/(1-i2) = (-5+9i+4)/2 = = -0,5+4,5i Ответ: А) 4-5i; Б) -9-i; В) -0,5+4,5i. Задание 3.Найти математическое ожидание и дисперсию, заданной законом распределения:
Математическое ожидание вычислим по формуле: М[X] = ∑Xi*Pi = -5*0,4 + 2*0,3 + 3*0,1 + 4*0,2 = -0,3 Дисперсию вычислим по формуле: D[X] = ∑Xi2*Pi – M2[X] = (-5)2*0,4 + 22*0,3 + 32*0,1 + 42*0,2 – (-0,3)2 = 15,21 Ответ: математическое ожидание М[Х] = -0,3, дисперсия D[X] = 15,21. Задание 4. Вычислить предел Решение: Подставим значение x0 в выражение: 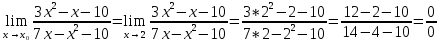 – неопределенность. Необходимо выполнить преобразования. – неопределенность. Необходимо выполнить преобразования.Разложим числитель на множители. Для этого найдем корни: 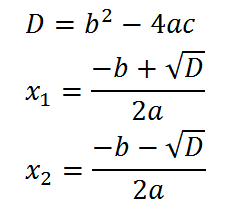 Вычислим дискриминант: D = (-1)2 – 4*3*(-10) = 1+120 = 121 Найдем корни: x1 = (-(-1) + 11)/(2*3) = 2 x2 = (-(-1) - 11)/(2*3) = -5/3 Т.о. 3х2-х-10 = 3*(x-2)*(x+5/3) = (x-2)*(3x+5) Разложим знаменатель на множители. Для этого найдем корни: 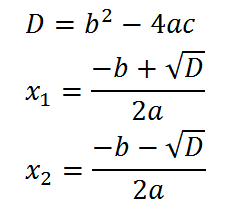 Вычислим дискриминант: D = 72 – 4*(-1)*(-10) = 49-40 = 9 Найдем корни: x1 = (-7+3)/(2*(-1)) = 2 x2 = (-7-3)/(2*(-1)) = 5 Т.о. 7x-x2-10 = (-1)*(x-2)*(x-5) = (x-2)*(5-x) Таким образом предел принимает следующий вид: 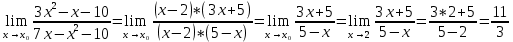 Ответ: 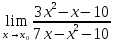 при x0 = 2 равен при x0 = 2 равен 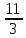 . .Задание 5.Найти производную функции Решение: 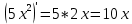 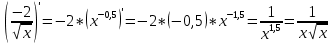 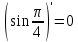 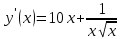 Ответ: 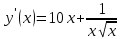 . .Задание 6.Вычислить неопределенный интеграл Решение: Воспользуемся формулой: ∫fg′=fg−∫f′g Пусть f=x, g’=cos(2x). Тогда: f’=x’=1, g=sin(2x)/2 ∫xcos(2x)dx=xsin(2x)/2−∫(sin(2x)/2)dx ∫(sin(2x)/2)dx Пусть 2х=u. Тогда: du/dx=2 dx=du/2 ∫(sin(2x)/2)dx = ∫((sin u)/2)*du/2 = (1/4)* ∫(sin u) du = ¼*(-cos u) = -¼*cos 2x ∫xcos(2x)dx=xsin(2x)/2+(cos 2x)/4+C Ответ: ∫xcos(2x)dx=xsin(2x)/2+(cos 2x)/4+C. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
