лекция 3. Лекции сформировать представление о декартовом произведении и декартовой степени множеств, раскрыть сущность понятия кортеж
 Скачать 76.48 Kb. Скачать 76.48 Kb.
|
|
Лекция 3 Кортежи и декартово произведение множеств. Декартова степень множества. цель лекции: сформировать представление о декартовом произведении и декартовой степени множеств, раскрыть сущность понятия кортеж. ключевые слова (термины): множество, кортеж, декартово произведение множеств, декартова степень множества. основные вопросы (положения) и краткое содержание: 1. Абстрактные законы операций над множествами Множество, его подмножества и законы сочетания подмножеств образуют алгебраическую систему, называемую булевой алгеброй. Ниже перечислены основные законы, действующие в булевых алгебрах. Законы для объединения и пересечения: 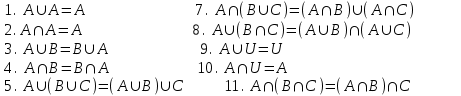 6. А 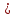 Ø = Ø 12. А Ø = Ø 12. А Ø=А Ø=АЗаконы для дополнений:  3. 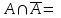 Ø 6. Ø 6. 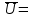 Ø. Ø.Законы для разностей множеств  Ø Ø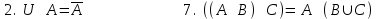 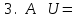 Ø Ø 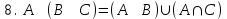 4. 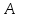 Ø = А 9. Ø = А 9. 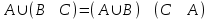 5. Ø А = Ø 10. 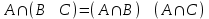 Доказательство каждого из перечисленных законов основано на определении равенства множеств и определений над множествами. 2. Кортежи и декартово произведение множеств Определение. Пусть даны множества 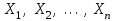 . Кортежем длины п , составленным из элементов этих множеств, называется конечная последовательность . Кортежем длины п , составленным из элементов этих множеств, называется конечная последовательность 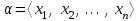 , где для всех k , где для всех k 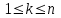 , имеем , имеем 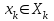 . .Элемент 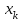 называется k-й координатой или k-й компонентой кортежа называется k-й координатой или k-й компонентой кортежа 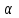 . .Два кортежа равны в том и только в том случае, когда они имеют одинаковую длину, причем их координаты, стоящие на местах с одинаковыми номерами, равны, т.е. кортежи 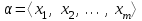 и и 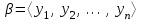 равны только в том случае, когда m = n, причем равны только в том случае, когда m = n, причем 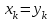 для всех для всех 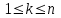 . .Кортежи длины два называются упорядоченными парами, длины три – упорядоченными тройками, … , длины п – упорядоченными п –ками. Для краткости речи слово «упорядоченные» часто опускают. Кортеж, не содержащий ни одной координаты , т.е кортеж длины 0, называется пустым. Основные отличия понятий кортежа и множества следующие: а) в множестве порядок элементов не играет роли, а кортежи, отличающиеся порядком элементов, различны, даже в случае, когда они имеют одинаковый состав; б) В множестве все элементы различны, а в кортеже координаты могут повторяться. В дальнейшем, чтобы различать множества и кортежи, будем элементы множества заключать в фигурные скобки , а координаты кортежа – в угловые. Пусть 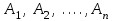 - некоторые множества. Их декартовым произведением называют множество, состоящее из кортежей вида - некоторые множества. Их декартовым произведением называют множество, состоящее из кортежей вида 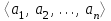 , где , где 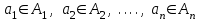 . Декартово произведение обозначается так: . Декартово произведение обозначается так: 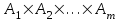 . .Произведение 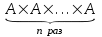 сокращенно обозначается как сокращенно обозначается как 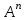 и называется декартовой п –й степенью множества А. и называется декартовой п –й степенью множества А.Декартовым произведением множеств X и Y называется множество всех пар (x; y), первая компонента которых xX, вторая компонента yY. Декартово произведение множеств X и Y обозначают XY и его можно записать: XY={(x;y)| xX;yY}. Декартово произведение можно образовывать как из элементов одного множества, так и двух множеств. Пример декартового произведения из двух множеств. . Пусть заданы два множества: X= {7, 5}, Y= {1, 4, 8}. Из этих множеств можно создать новое множество, перечислив все упорядоченные пары: XY={(7;1), (7;4), (7;8), (5;1), (5;4), (5;8)}. В полученном множестве каждый элемент является упорядоченной парой, в которой первая компонента принадлежит множеству X, вторая множеству Y. Пример декартового произведения из одного множества. Пусть на множестве Х={3, 5, 7} задано отношение «меньше» (т.е. первый элемент меньше второго, второй меньше третьего). Записать декартово произведение X Х. Решение. Декартово произведение X Х может быть записано в виде множества из упорядоченных пар: X Х ={(3;3),(3;5),(3;7),(5;3),(5;5),(5;7),(7;3),(7;5),(7;7)}. Из этого множества следует выбрать элементы, которые должны удовлетворять отношению «меньше». В результате получится новое множество из упорядоченных пар: ={(3;5),(3;7),(5;7)}. В новом множестве все пары являются элементами декартова произведения XX. Отношение «меньше» на множестве Х является подмножеством декартова произведения XX. вопросы для самоконтроля: Дайте определение кортежа. Отличие понятия кортежа от множества. критерии оценки достижения обучающимися результатов обучения: Даны в силлабусе. рекомендуемая литература: Дана в силлабусе. |
