Лекции. Лекции 4 и 5 по дисциплине (модулю) Компьютерные технологии в проектировании
 Скачать 71.96 Kb. Скачать 71.96 Kb.
|
|
МИНОБРНАУКИ РОССИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «Тульский государственный университет» ИВТС им. В.П.Грязева Кафедра «Электроэнергетики» Лекции №4 и №5 по дисциплине (модулю) «Компьютерные технологии в проектировании» основной профессиональной образовательной программы высшего образования – программы бакалавриата по направлению подготовки (специальности) 13.03.02 Электроэнергетика и электротехника с направленностью (профилем) (со специализацией) Электроснабжение Электрооборудование и электрохозяйство предприятий, организаций и учреждений Форма(ы) обучения: очная, заочная Идентификационный номер образовательной программы: 130302-01-19, 130302-02-19 Тула 2020 год Разработчик(и) методических указаний ____Горелов Ю.И., доцент каф.Э, , к.т.н, доц. ____ _______________ (ФИО, должность, ученая степень, ученое звание) (подпись) ____________________________________________ _______________ (ФИО, должность, ученая степень, ученое звание) (подпись)Операции с векторами и матрицами.По определению, если матрица квадратная и не сингулярная, уравнения АХ =I и XA = I имеют одно и то же самое решение X. Это решение называют обратной матрицей A и обозначают 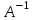 , в МАТЛАБ она может быть вычислена при помощи функции inv. Детерминант (определитель) матрицы может быть вычислен при помощи функции det. , в МАТЛАБ она может быть вычислена при помощи функции inv. Детерминант (определитель) матрицы может быть вычислен при помощи функции det.Например A = 1 1 1 1 2 3 1 3 6 d = det (A) X = inv (A) d = 1 X = 3 – 3 1 -3 5 -2 1 - 2 1 Если матрица А квадратная и не сингулярная, то без ошибки округления, X = inv (A) *B дает тот же самый результат, что и Х= A\B . Но вычисления Х= A\B, предпочтительны, потому что они требуют меньшего количества компьютерного времени, меньшего количества памяти, и имеют лучшие свойства обнаружения ошибок. Прямоугольные матрицы не имеют обратных и детерминантов. По крайней мере одно из уравнений АХ =I и XA = I не имеет решения. В математике в этом случае вместо обращения матриц используют так называемые псевдообращения матриц, которое в МАТЛАБ имеет в смысл Мура-Пендроуза и реализуется функцией pinv. Например A=[1 2 3; 5 6 7] A = 1 2 3 5 6 7 >> pinv(A) ans = -0.8333 0.3333 -0.0833 0.0833 0.6667 -0.1667 >> A*pinv(A) ans = 1.0000 -0.0000 -0.0000 1.0000 Если число строк матрицы  больше числа столбцов больше числа столбцов 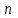 и ранг матрицы равен и ранг матрицы равен 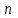 , то , то x = A\b x = pinv(A)*b x = inv(A'*A)*A'*b теоретически вычисляют одно и то же решение наименьших квадратов Х, хотя оператор наклонной черты влево делает это быстрее. Однако, если А не имеет полного ранга, то есть ее ранг меньше 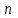 , то решение наименьших квадратов не единственно. Есть много векторов Х, которые минимизируют норму (A*x-b) , то решение наименьших квадратов не единственно. Есть много векторов Х, которые минимизируют норму (A*x-b)Решение, вычисленное x = A\b - главное решение; оно имеет в худшем случае r компонентов отличных от нуля, где r - ранг A. Решение, вычисленное по x = pinv (A) *b - решение минимизирующее нормы (A*x-b) и (Х). Попытка вычислять решение с x = inv ('*A) *A '*b терпит неудачу, потому что '*A сингулярна. Пример, А = 1 2 3 4 5 6 7 8 9 10 11 12 не имеет полного ранга. Его второй столбец - среднее число первых и третьих столбцов. Если b = 2 5 8 11 то есть является вторым столбцом, то очевидное решение A*x = b - x = [0 1 0] '. Но ни один из подходов не вычисляет этот x. Оператор наклонной черты влево дает x = A\b Warning: Rank deficient, rank = 2. x = 0.5000 0 0.5000 Это решение имеет два компонента отличных от нуля. Псевдообратный подход дает y = pinv (A) *b y = 0.3333 0.3333 0.3333 Нет никакого предупреждения о неточности ранга. Но норма (y) = 0.5774 - меньше чем норма (x) = 0.7071. Наконец z = inv(A'*A)*A'*b fails completely. Warning: Matrix is singular to working precision. z = Inf Inf Inf. Разложение на множители Холецкого выражает симметрическую матрицу как произведение 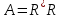 где R - верхняя треугольная матрица. Не всякую симметрическую матрицу можно представить этим способом; матрицы, которые имеют такое разложение на множители, должны быть положительно определенными. Это обычно бывает, когда все диагональные элементы положительны, а недиагональные элементы являются "не слишком большими". Например A = 1 1 1 1 1 1 1 2 3 4 5 6 1 3 6 10 15 21 1 4 10 20 35 56 1 5 15 35 70 126 1 6 21 56 126 252 R = chol (A) R = 1 1 1 1 1 1 0 1 2 3 4 5 0 0 1 3 6 10 0 0 0 1 4 10 0 0 0 0 1 5 0 0 0 0 0 1 Разложение на множители по Холецкому позволяет линейной системе 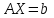 быть замененной на  Поскольку оператор наклонной черты влево распознает треугольные системы, то последнее уравнение может быть решено в MATLAB достаточно быстро при записи x = R \ (R '\b) LU разложение на множители, или Гауссовское преобразование, выражают любую квадратную матрицу как произведение некоторой матрицы, представляющей собой действие некоторой перестановки на нижнюю треугольную матрицу с единичной диагональю и верхней треугольной матрицы, 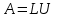 где L – перестановка нижней треугольной матрицы с 1 на ее диагонали, и U - верхняя треугольная матрица. Перестановки необходимы и по теоретическим и по вычислительным причинам. Матрица не может быть выражена как произведение треугольных матриц, не обмениваясь его двумя рядами. Например A=[1 2 3; 5 6 7; 4 11 3] A = 1 2 3 5 6 7 4 11 3 >> [L U]=lu(A) L = 0.2000 0.1290 1.0000 1.0000 0 0 0.8000 1.0000 0 U = 5.0000 6.0000 7.0000 0 6.2000 -2.6000 0 0 1.9355 LU разложение на множители позволяет линейную систему A*x = b решить очень быстро при помощи x = U \ (L\b) Например A = 1 2 3 5 6 7 4 11 3 >> [L U]=lu(A) L = 0.2000 0.1290 1.0000 1.0000 0 0 0.8000 1.0000 0 U = 5.0000 6.0000 7.0000 0 6.2000 -2.6000 0 0 1.9355 >> b=[5; 3; 7] b = 5 3 7 >> x = U \ (L\b) x = -4.0333 1.5667 1.9667 Детерминант и обратная матрица могут быть вычислены с использованием LU разложения на множители det (A) = det (L) *det (U) и inv (A) = inv (U) *inv (L) >> det (L) *det (U) ans = 60.0000 >> inv (U) *inv (L) ans = -0.9833 0.4500 -0.0667 0.2167 -0.1500 0.1333 0.5167 -0.0500 -0.0667 Графическая интерпретация вычислений.Функции одной переменной y(x) находят широкое применение в практике математических и других расчетов, а также в технике компьютерного математического моделирования. Для отображения таких функций используются графики в Декартовой системе координат. При этом строятся две оси – горизонтальная X и вертикальная Y – и задаются координаты x и y, определяющие узловые точки y(x). Эти точки соединяются друг с другом отрезками прямых линий. Поскольку MATLAB представляет собой матричную систему, совокупность точек y(x) задается векторами X и Y одинакового размера. Синтаксис: plot(x,y) plot(y) plot(x,y,’s’) plot(x1,y1,’s1’,x2,y2,’s2’,…) plot(x,y) − строит график функции y(x). Если X или Y матрица, то строятся графики по данным в матрице. plot(y) − строит график функции y(i), при этом значения берутся из вектора Y, а i представляет собой индекс соответствующего элемента. Если Y содержит комплексные элементы, то выполняется команда plot(real(Y), imag(Y)). Во всех других случаях мнимая часть игнорируется. plot(x,y,’s’) − строит график функции y(x) но с заданием типа линии графика в виде строковой константы, которая может принимать следующие значения: 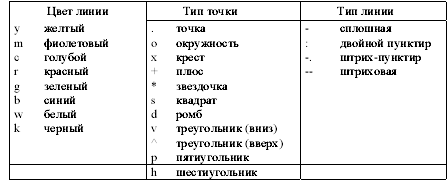 Таким образом, с помощью константы s, можно изменять цвет линии, представлять узловые точки различными знаками, менять тип линии графика. Функция plot(x1,y1,’s1’,x2,y2,’s2’,…) строит на одном графике ряд линий, представленных данными вида (x,y,’s’). При отсутствии указания на цвет линий и точек он выбирается автоматически одним из шести табличных цветов (исключая белый). Если линий больше шести, то выбор цветов повторяется. Для монохромных систем линии выделяются стилем. Пример: » %Графики трех функций со спецификацией линий каждого графика » x = - 2*pi : 0.1*pi : 2*pi ; » y1 = sin(x); » y2 = sin(x).^2; » y3 = sin(x).^3; » plot(x,y1,’-m’,x,y2,’+r’,x,y3,’- -ok’) Для построения графиков функций со значениями x и y, изменяющимися в широких пределах, нередко используются логарифмические масштабы. Для этого применяется команда loglog(…), синтаксис которой аналогичен рассмотренному для команды plot. Пример: » % График экспоненциальной функции в логарифмическом масштабе » x=logspace(-1,3); » loglog(x,exp(x)./x,'k'); » grid on Графикифункцийвполулогарифмическоммасштабе В некоторых случаях предпочтителен полулогарифмический масштаб графиков, когда по одной оси задается логарифмический масштаб, а по другой – линейный. semilogx(…) – строит график функции в логарифмическом масштабе (основание 10) по оси X и линейным по оси Y. semilogy(…) – строит график функции в логарифмическом масштабе по оси Y и линейным по оси X. Синтаксис команды аналогичен синтаксису команды plot. hist Построение графика в виде гистограммы Классическая гистограмма характеризует число попаданий значений элементов вектора Y в М интервалов с представлением этих чисел в виде столбиковой диаграммы. Получение данных для гистограммы выполняется функцией hist, имеющей синтаксис: N = hist(Y) – возвращает вектор числа попаданий для 10 интервалов. Если Y – матрица, то выдаются данные по числу попаданий в ее столбцы; N = hist(Y,M) – возвращает число попаданий для элементов вектора Y с центральными отчетами, заданными элементами вектора X; [N,X] = hist(…) – возвращает числа попаданий в интервалы и данные о центрах интервалов; hist(…) – с синтаксисом аналогичным приведенному выше, строит график гистограммы. Пример: Построим гистограмму для 1000 случайных чисел и выведем вектор с данными и числах их попаданий в интервалы, заданные вектором X. » % Построение гистограммы для 1000 случайных чисел » x=-3:0.2:3; » y=randn(1000,1); » hist(y,x); » h=hist(y,x) h = Columns 1 through 12 0 0 3 7 8 9 11 23 33 43 57 55 Columns 13 through 24 70 62 83 87 93 68 70 65 41 35 27 21 Columns 25 through 31 12 5 6 3 2 1 0 stairs - лестничный график функции Лестничные графики представляют собой ступеньки, с огибающей, представленной функцией y(x). Такие графики используются, например, для отображения процессов квантования функции y(x), представленной рядом своих отсчетов. При этом в промежутках между отсчетами значения функции считаются постоянными и равными величине последнего отсчета. Синтаксис функции: stairs(Y) – строит лестничный график по данным вектора Y; stairs(X,Y) – строит лестничный график по данным вектора Y с координатами х переходов от ступеньки к ступеньке заданными значениями элементов вектора X (они должны идти в возрастающем порядке); stairs(…,S) – аналогична по действию вышеописанным командам, но строит график линиями, стиль которых задается строками S (см. оператор plot). Пример: » % Лестничный график функции x^2 » x=0:0.25:10; » stairs(x,x.^2); polar - график в полярной системе координат В полярной системе координат любая точка представляется как конец радиус-вектора, исходящего из начала системы координат, имеющего длину RHO и угол THETA (обычно меняется от 0 до 2π). Синтаксис команды: polar(theta,rho) – строит график в полярной системе координат, представляющий собой положение конца радиус-вектора; polar(theta,rho,S) – аналогична предыдущей команде, но позволяет задавать стиль построения аналогично оператору plot. Пример: » % График функции sin(5*t) в полярной системе координат » t=0:pi/50:2*pi; » polar(t,sin(5*t)) compass построение векторов Иногда желательно построение ряда радиус-векторов в их обычном виде, то есть в виде стрелок, исходящих из начала координат и имеющих угол и длину, которые определяются действительной и мнимой частями комплексных чисел, представляющих данные векторы. Синтаксис: compass(U,V) – сроит графики радиус-векторов с компонентами (U,V), представляющими действительную и мнимую части каждого из них; compass(Z) – эквивалентна compass(real(Z),imag(Z)); compass(U,V,S) – аналогичны представленным выше командам, но позволяет задать спецификацию линий построения аналогично команде plot; H=compass(…) – возвращает значения длин радиус-векторов. Пример: » % Построение радиус-векторов для вектора Z с комплексными » % элементами » Z=[-1+2i,-2-3i,2+3i,5+2i]; » compass(Z) contour Построение контурных графиков Контурные график являются попыткой отобразить на плоскости функции двух переменных вида z(x,y). Их можно представить в виде совокупности линий равного уровня, которые получаются, если трехмерная поверхность пересекается рядом плоскостей, расположенных параллельно друг другу. При этом контурный график представляет совокупность спроецированных на плоскость y(x) линий пересечения поверхности z(x,y) плоскостями. Синтаксис: contour(z) – строит контурный график по данным матрицы z с автоматическим диапазоном изменения x и y; contour(x,y,z) – строит контурный график по данным матрицы z с указанием спецификаций для x и y; contour(z,N) и contour(x,y,z,N) – дают построения аналогичные ранее описанным, с заданием N линий равного уровня (по умолчанию N = 10); contour(z,V) и contour(x,y,z,V) – строят линии равного уровня для высот, указанных значениями элементов вектора V; [C,H] = contour(…) – возвращает дескриптор – матрицу C и вектор столбцов H. Они используются как входные параметры для команды clabel (см. далее); contour(…,S) – позволяет использовать перечисленные выше функции с указанием спецификации линий, аналогично команде plot. Пример: » % Построение контурного графика объекта peaks » z=peaks(27); » contour(z,15) comet Движение точки по плоскости Синтаксис: comet(Y) comet(X, Y) comet(X, Y, p) Для отображения движения точки по траектории используется функция comet. При этом движущаяся точка напоминает ядро кометы с хвостом. Функции comet(Y) и comet(X,Y) отображают движение “кометы” по траектории, заданной вектором Y и векторами X и Y соответственно. comet(X,Y,p) - аналогична предшествующим, но позволяет задавать длину хвоста кометы как p*length(Y) . По умолчанию значение p = 0,1. На черно-белом рисунке “хвост кометы” заметить трудно, поскольку он представляет собой отрезок линии с цветом, отличающимся от цвета линии основной части графика. meshgrid Функция создания массивов трехмерной графики Трехмерная поверхность обычно описывается функцией двух переменных z(x,y). Специфика построения трехмерных графиков требует не просто задания ряда значений x и y, то есть векторов x и y – она требует определения двумерных массивов для X и Y матриц. Синтаксис: [X,Y] = meshgrid(x,y) – преобразует область, заданную векторами x и y в массивы X и Y, которые могут быть использованы для вычисления функции двух переменных и построения трехмерных графиков. Строки выходного массива X являются копиями вектора x, а столбцы Y – копиями вектора y; meshgrid(x) – аналогична [X,Y] = meshgrid(x,x); [X,Y,Z] = meshgrid(x,y,z) – возвращает трехмерные массивы, используемые для вычисления функций трех переменных и построения трехмерных 3D-графиков. plot3 Функция построения трехмерных графиков линиями Синтаксис: plot3(x,y,z) – строит массив точек, представленных векторами x, y и z, соединяя их отрезками прямых. Команда имеет ограниченное применение, т.к. строит не поверхность , а пространственную кривую; plot3(X,Y,Z) – строит точки с координатами X(i,:), Y(i,:) b Z(i,:) и соединяет их отрезками прямой, получая таким образом трехмерную поверхность; plot3(X,Y,Z,S) – обеспечивает аналогичные построения, но со спецификацией линий и точек, соответствующих синтаксису команды plot. Пример: » x=-3:0.1:3; » y=x; » z=x.^2+y.^2; » subplot(2,1,1),plot3(x,y,z),grid on » [x,y]=meshgrid(x,y); » z=x.^2+y.^2; » subplot(2,1,2),plot3(x,y,z),grid on mesh Сеточные 3D-графики с функциональной окраской Наиболее представительными и наглядными являются сеточные графики трехмерных поверхностей с заданной или функциональной окраской. Синтаксис: mesh(X,Y,Z) – выводит в графическое окно сетчатую поверхность Z(X,Y) с функциональной окраской, при которой цвет задается высотой поверхности. Возможна также форма mesh(Z); meshc(…) – по синтаксису аналогична предыдущим, но строит график поверхности, объединенный с проекциями линий равного уровня (графика типа contour); meshz(…) – аналогичный синтаксис, но строит поверхность в виде столбиков. Пример: » [x,y]=meshgrid([-3:0.1:3]); » z=x.^2+y.^2; » subplot(2,1,1),mesh(x,y,z) » subplot(2,1,2),meshc(x,y,z) surf Затененные сеточные 3D-графики Синтаксис: surf(X, Y, Z, C) - вывод на экран сетчатой поверхности для значений массива Z, определенных на множестве значений массивов X и Y. Цвет массива определяется массивом C; surf(Z, C) - использует сетку, которая определяется одномерными массивами х = 1: n и y = 1: m; surf(X, Y, Z) и surf(Z) используют в качестве массива цвета C = Z, то есть цвет в этом случае пропорционален высоте поверхности; surf – возвращает свойства объекта surface. Благодаря функциональной окраске график поверхности гораздо более выразителен, чем при построении поверхности функцией mesh, причем даже в том случае, когда цветной график печатается в черно-белом виде (в этом случае лучше использовать функцию colormap(gray), выполняющую окраску фигуры в тонах серого цвета). Вспомогательные графические функции figure Активизация графического окна Синтаксис: figure(n) - данная команда делает активным графическое окно с номером n (если такое окно существует) или создает пустое графическое окно. axis Масштабирование осей и вывод на экран Синтаксис: axis([xmin xmax ymin ymax]) axis(‘auto’) axis(axis) axis(‘square’) axis(‘equal’) axis([xmin xmax ymin ymax]) - устанавливает масштаб по осям x, y для активного графического окна (для трехмерных графиков добавятся аргументы zmin и zmax). axis(‘auto’) - возвращает масштаб по осям к исходным значениям (принятым по умолчанию). axis(axis) - фиксирует текущие значения масштабов по осям для последующих графиков. axis(‘square’) - устанавливает одинаковый диапазон изменения переменных по осям. axis(‘equal’) - устанавливает масштаб, который обеспечивает одинаковые расстояния между метками по осям x и y. grid Нанесение сетки Синтаксис: grid on - наносит координатную сетку на текущие оси; grid off - удаляет координатную сетку; grid - выполняет роль переключателя с одной функции на другую. hold Управление режимом сохранения текущего окна Синтаксис: hold on - включает режим сохранения текущего графика и свойств объекта axis, так что последующие команды приведет к добавлению новых графиков в активном графическом окне; hold off - выключает режим сохранения текущего графика; hold - реализует переключение с одного режима на другой. subplot Разбиение графического окна Синтаксис: subplot(mnp) - данная команда выполняется перед обращение к функциям построения графиков для одновременной выдачи нескольких графиков (каждый со своим объектом axis) в различных частях графического окна. значение m указывает, на сколько частей разбивается окно по горизонтали, n - по вертикали, а р - номер позиции, куда будет выводиться очередной график. Эта же команда используется для перехода от одного подокна к другому. Пример: » x=-1:0.1:1; » y1=sin(x); » subplot(211),plot(x,y1) » y2=log(abs(y1)); Warning: Log of zero. » subplot(212),plot(x,y2) zoom Увеличение масштабов графика Синтаксис: zoom on (off) - включает (выключает) режим масштабирования активного графика. Удерживая ЛКМ вы можете выделить интересующую Вас область графика, которая будет увеличена затем до размеров текущего графического окна; zoom out - возвращает график в исходное положение. title Установка титульной надписи Синтаксис: title('<текст>') Команда title('<текст>') размещает текст над 2D- и 3D-графиком. xlabel, ylabel, zlabel Установка осевых надписей Синтаксис: xlabel('<текст>') ylabel('<текст>') zlabel ('<текст>') xlabel('<текст>') - помещает текст для двумерного графика вдоль оси х, для трехмерного графика - вдоль оси х либо под графиком. ylabel('<текст>') - помещает текст для двумерного графика вдоль оси у, для трехмерного графика - вдоль оси у либо под графиком. zlabel ('<текст>') - помещает текст вдоль оси z трехмерного графика. Повторное использование команды приводит к замене старого текста новым. clabel Маркировка линий равного уровня Синтаксис: clabel(C) clabel(C, v) clabel(C, 'manual') clabel(C) - добавляет метки к линиям уровня в случайно выбранных позициях. clabel(C, v) - маркирует линии уровня контура, заданные в векторе v. clabel(C, 'manual') - маркирует линии уровней в позициях, указываемых с помощью мыши. Нажатие клавиши Return или правой кнопки мыши завершает маркировку. Если мышь недоступна, то можно использовать клавишу пробела для перехода между линиями уровней и “клавиши-стрелки” для перемещения перекрестия. Пример: » [X,Y]=meshgrid([-3:0.1:3]); » Z=sin(X)./(X.^2+Y.^2+0.3); » C=contour(X,Y,Z,10); » colormap(gray) » clabel(C) text Ввод надписи в любое место графика Синтаксис: text(x, у, '<текст>') text(x, y, z, '<текст>') text(x, у, '<текст>') - помещает в заданной точке (х, у) двумерного графика начало текста, указанного в качестве третьего аргумента. Если х и у одномерные массивы, заданный текст помещается во все позиции, определяемые координатами [x(i) y(i)]. text(x, у, z, '<текст>') - выводит текст на трехмерный график. Приведем примеры написания команд без показа их графической реализации. Создать графическое окно и написать символ 'х' в трех точках с координатами (1, 1), (5, 10), (10, 20): plot([1 5 10], [1 10 20], 'х') Написать, начиная с позиции (5, 10), 'Action point': text(5, 10, 'Action point') Написать, в позициях (2, 10), (7, 16) 'Нет активных точек': text([2 7], [10 16], ‘Нет активных точек’) gtext Ввод текста на график с помощью мыши Cинтаксис: gtext('<текст>') Команда gtext('<текст>') высвечивает в активном графическом окне перекрестие, перемещение которого позволяет указать место ввода заданного текста; по завершении позиционирования нажатие кнопки мыши или любой клавиши вводит заданный текст. Пример. Разместим на графике функции у = sin(x)/x маркер "Скорость": » x=1e-6:0.05:10; » plot(x,sin(x)./x) » grid » gtext('Скорость') legend Вывод пояснения Синтаксис: legend('<текст1>', '<текст2> ', ‘<текст3>', ...) legend(' legend(h,...) legend(M) legend(h, M) legend off legend(..., n) legend('<текст1>', '<текст2> ', ‘<текст3>', ...) - добавляет к текущему графику пояснение в виде указанных текстовых строк. legend(' legend(h. ...) - добавляет пояснение к графику с дескриптором h. Команды legend(M) и legend(h, M), где М - массив строк, также допустимы для формирования пояснения. Следует помнить, что строки массива М должны иметь одинаковую длину. legend off - удаляет пояснение с текущего графика. legend(..., n) - устанавливает предельное количество позиций для размещения пояснения. Если оказывается, что в области графика места недостаточно, график перестраивается и пояснение размещается вне пределов графика. Если n = -1, то пояснение размещается вне области графика. Если n = 0, то пояснение размещается в области графика, если места для этого достаточно. Для перемещения пояснения следует нажать левую кнопку мыши, находясь в этой области, а затем переместить пояснение в нужную позицию. Замечание: Для того чтобы избежать пересечения пояснения с линиями графика или нанесенной сеткой, необходимо текущему графическому объекту axes присвоить дескриптор пояснения: hi = legend(....) axes(hl) print -dbitmap colorbar Вывод шкалы палитры Синтаксис: colorbar('vert') colorbar('horiz') colorbar(h) colorbar colorbar('vert') - добавляет к текущему графику вертикальную шкалу палитры. colorbar('horiz') - добавляет к текущему графику горизонтальную шкалу палитры. colorbar(h) - добавляет к графику с дескриптором h шкалу палитры. Размещение шкалы реализуется автоматически в зависимости от соотношения ширины и высоты графика. Команда colorbar без аргументов размещает на текущем графике новую вертикальную шкалу палитры или обновляет прежнюю. |
