Лабораторная. Лаб. работа 5. Лекции, либо в учебном пособии Эконометрика. Анализ временных рядов
 Скачать 1.6 Mb. Скачать 1.6 Mb.
|
|
Лабораторная работа по одномерным временным рядам Сезонная декомпозиция. Теоретическую часть этого раздела см. либо в лекции, либо в учебном пособии «Эконометрика. Анализ временных рядов» Как известно, уровни элементов временного ряда могут формироваться под воздействием трёх компонент; трендовой (Tt), сезонной (St) и случайной (It). Будем рассматривать мультипликативную модель временного ряда, когда все эти компоненты объединены знаком умножить: yt = Tt*St*It. Рассмотрим следующий временной ряд продаж за 6 лет поквартально. 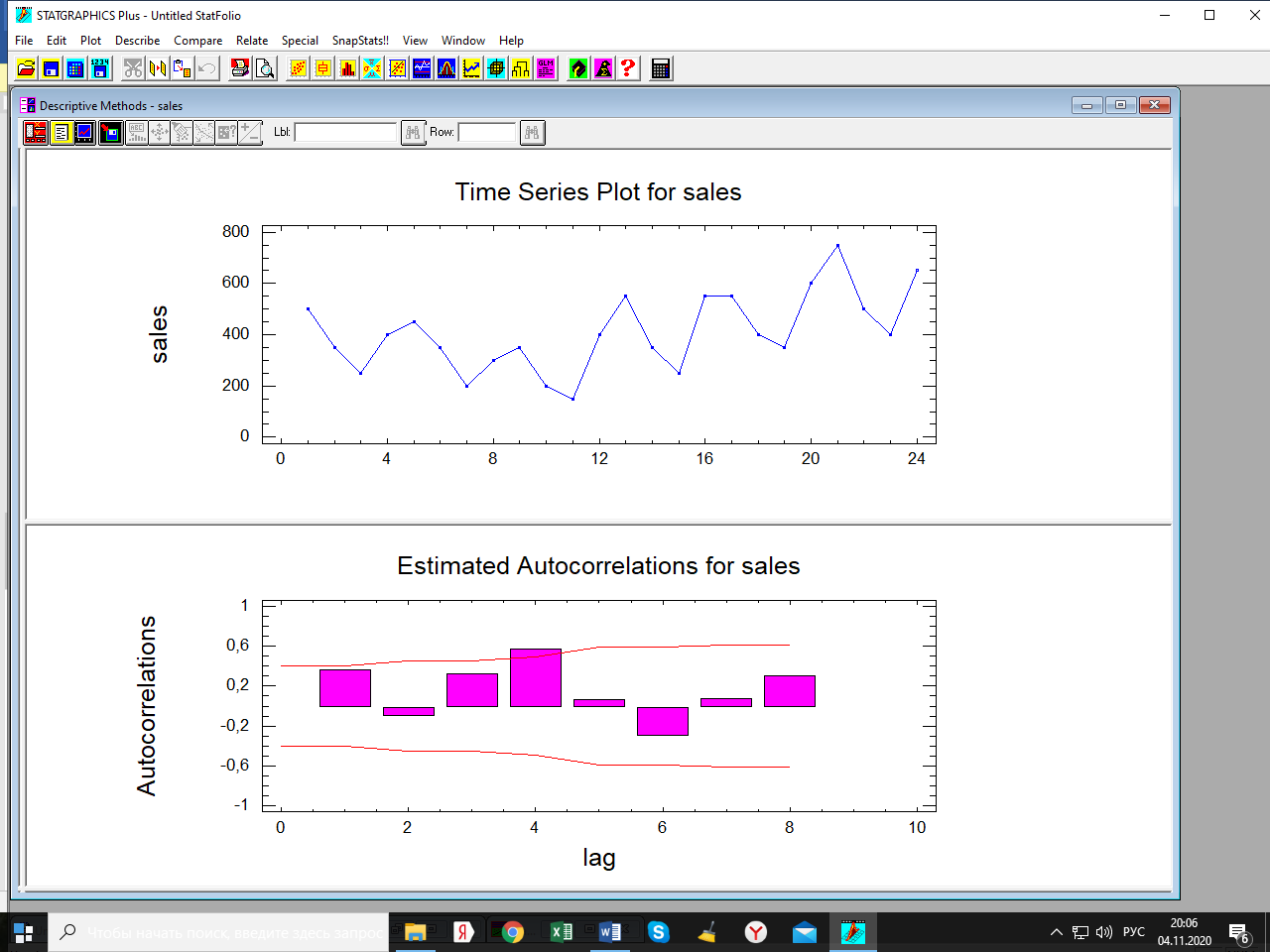 Здесь приведены горизонтальный график рада и его коррелограмма (график автокорреляционной функции). Коррелограма показывает наличие тренда (первый высокий столбик) и сезонность с длиной сезонности, равной четырём (четвёртый высокий столбик). Ниже приведена реализация этого метода программой Statgraphics. 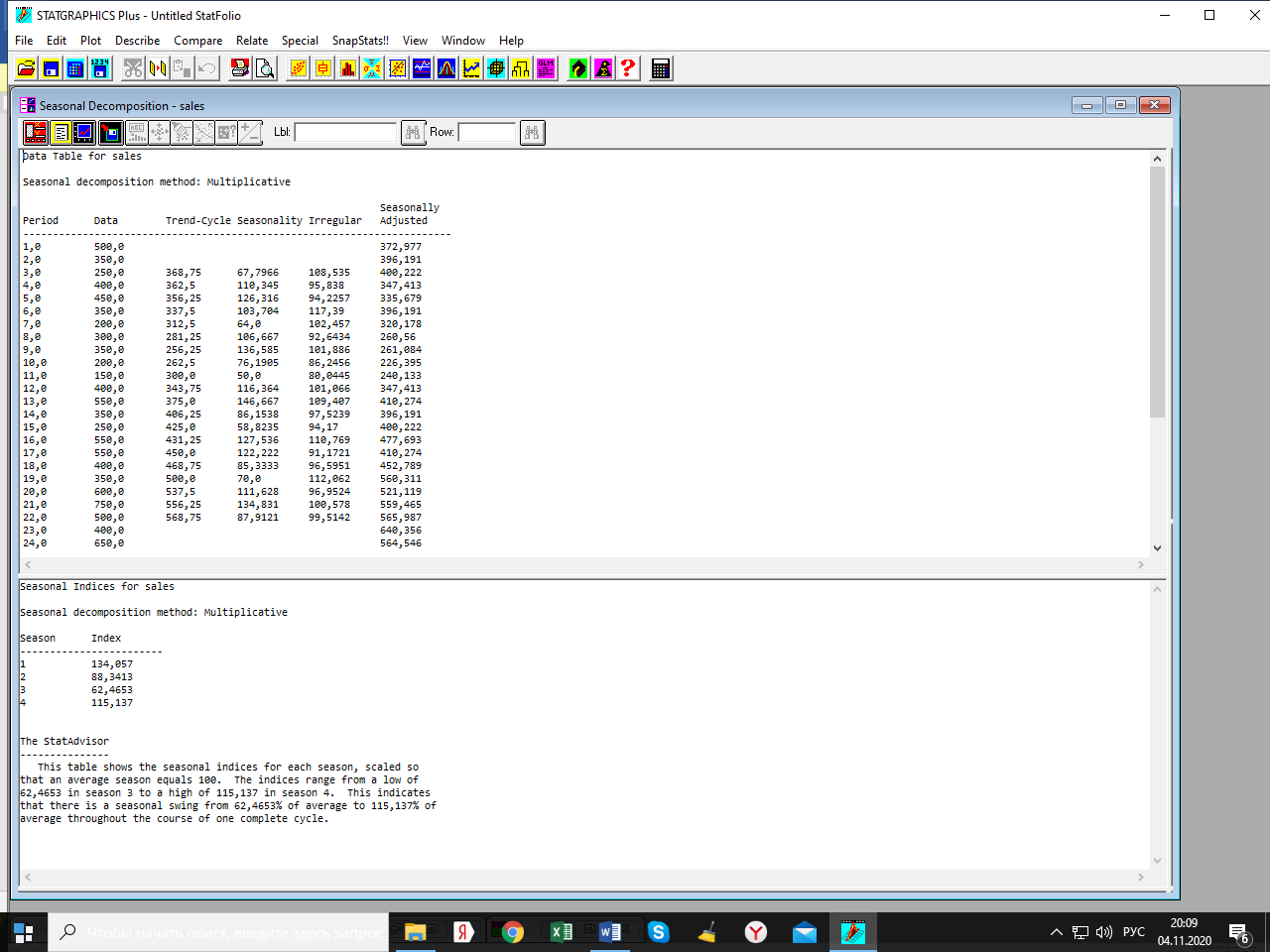 Первый столбик цифр – номера кварталов. Второй – уровни ряда, график которого – выше. Метод сезонной декомпозиции включает в себя несколько этапов: выделяется трендовая компонента путём применения центрированной скользящей средней (третий столбик цифр и первый график; точки–исходные данные, красная линия–линия тренда); затем путём деления элементов временного ряда на полученные уровни трендовой компоненты получаются уровни сезонно-случайных компонент (yt/Tt = St*It) (четвёртый столбик цифр); путём усреднения по кварталам случайной компоненты получаем индекс сезонности (нижняя часть таблицы и график индекса – второй график). Из индекса сезонности видно, что в первом квартале объёмы продаж на 34,6% выше, чем в среднем по тренду, во втором и третьем кварталам ниже соответственно на 12% и на 38% (цифры приведены с округлением); пятый столбик и третий график–это случайная компонента (yt/(Tt*St)= It): шестой столбик и четвёртый график – это данные, исправленные на сезонность (yt/ St = Tt*It). Геометрическая иллюстрация метода мезонной декомпозиции приведена ниже: 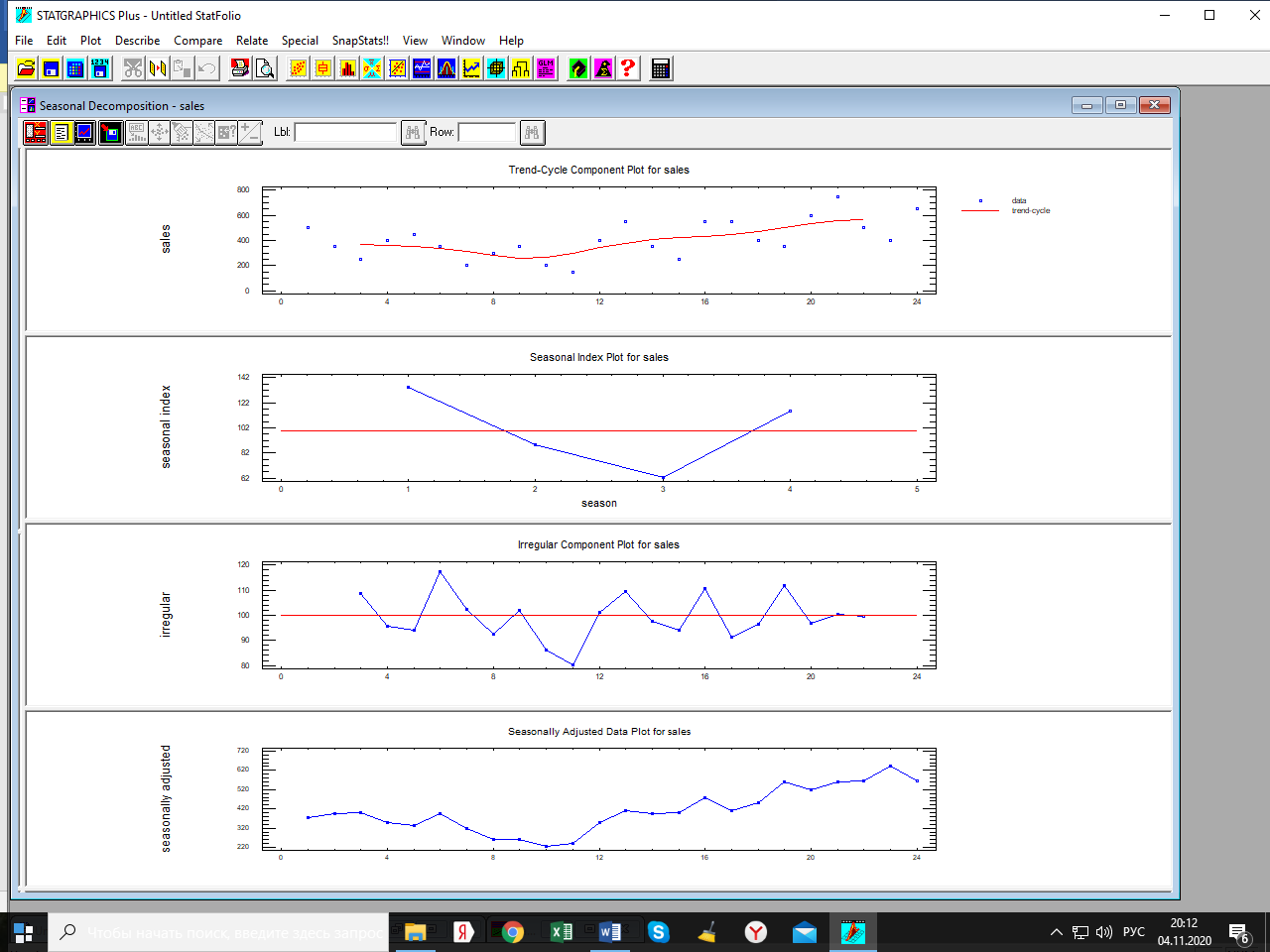 Последние данные нужны для получения линии тренда в виде функции от времени. Такая процедура называется аналитическое выравнивание уровней элементов временного ряда. Реализуется эта процедура разделом «прогнозирование» в этой программе. Сохранив эти данные под именем sadjusted, получим следующий отчёт о работе этой процедуры. 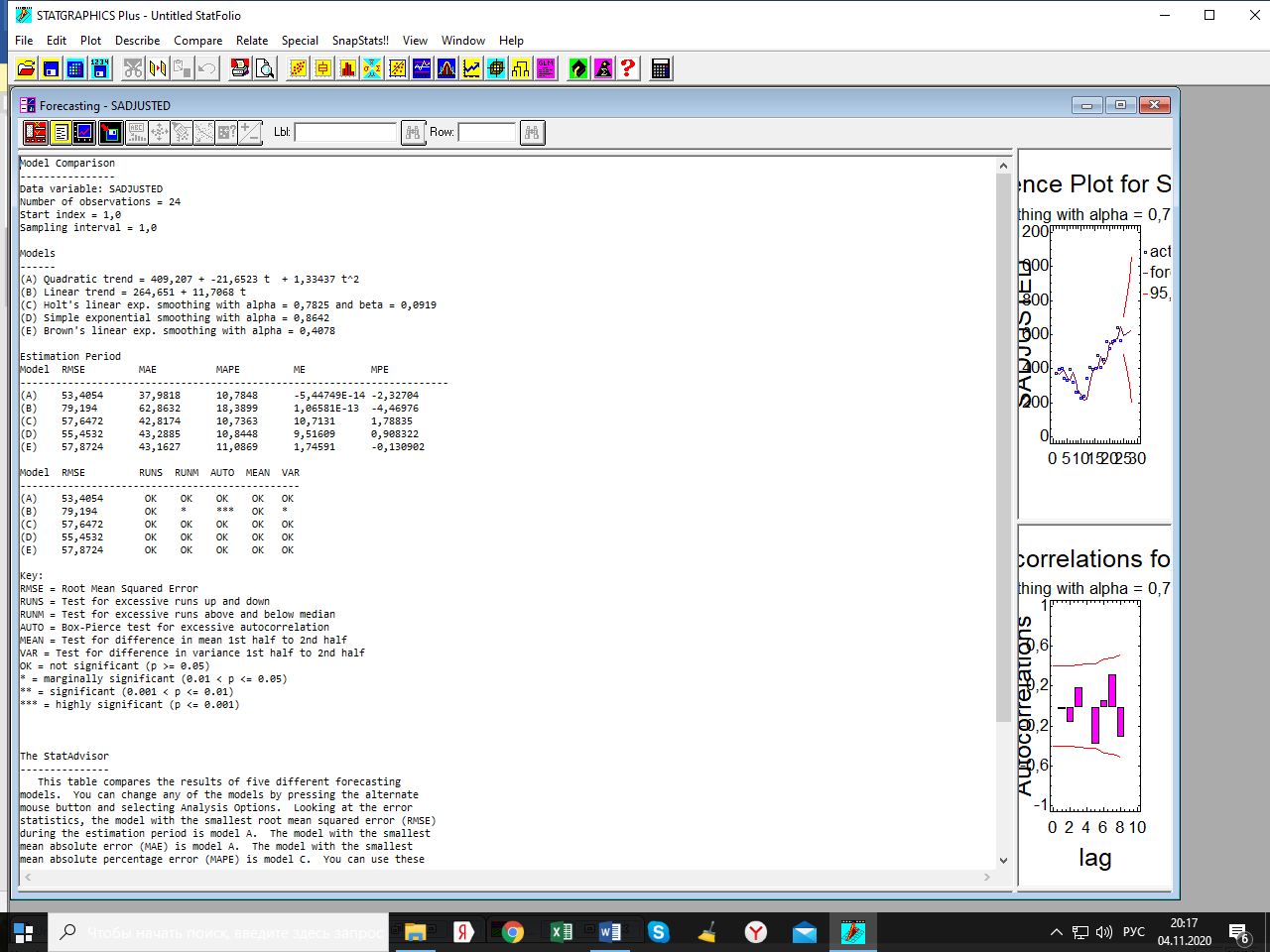 Для сравнения здесь приведены пять моделей: (А) – квадратичный тренд, (В) – линейный тренд, (С) – Хольта линейное экспоненциальное сглаживание, (D) – простая экспоненциальная сглаженная и (Е) – Брауна линейное экспоненциальное сглаживание. Ниже приведены показатели точности прогноза, по минимальному значению которых выбирается наиболее точная модель. Как видим, более точная модель – квадратичный тренд. У него наименьшая ошибка прогноза (RMSE). Выбрав эту модель, получили прогноз с доверительными границами и ниже – график прогноза и автокорреляционную функцию остатков модели. Коррелограма показывает, что модель адекватна исходным данным (данным, исправленным на сезонность), т.к. остатки модели являются «белым шумом». При защите работы надо будет проанализировать все модели. 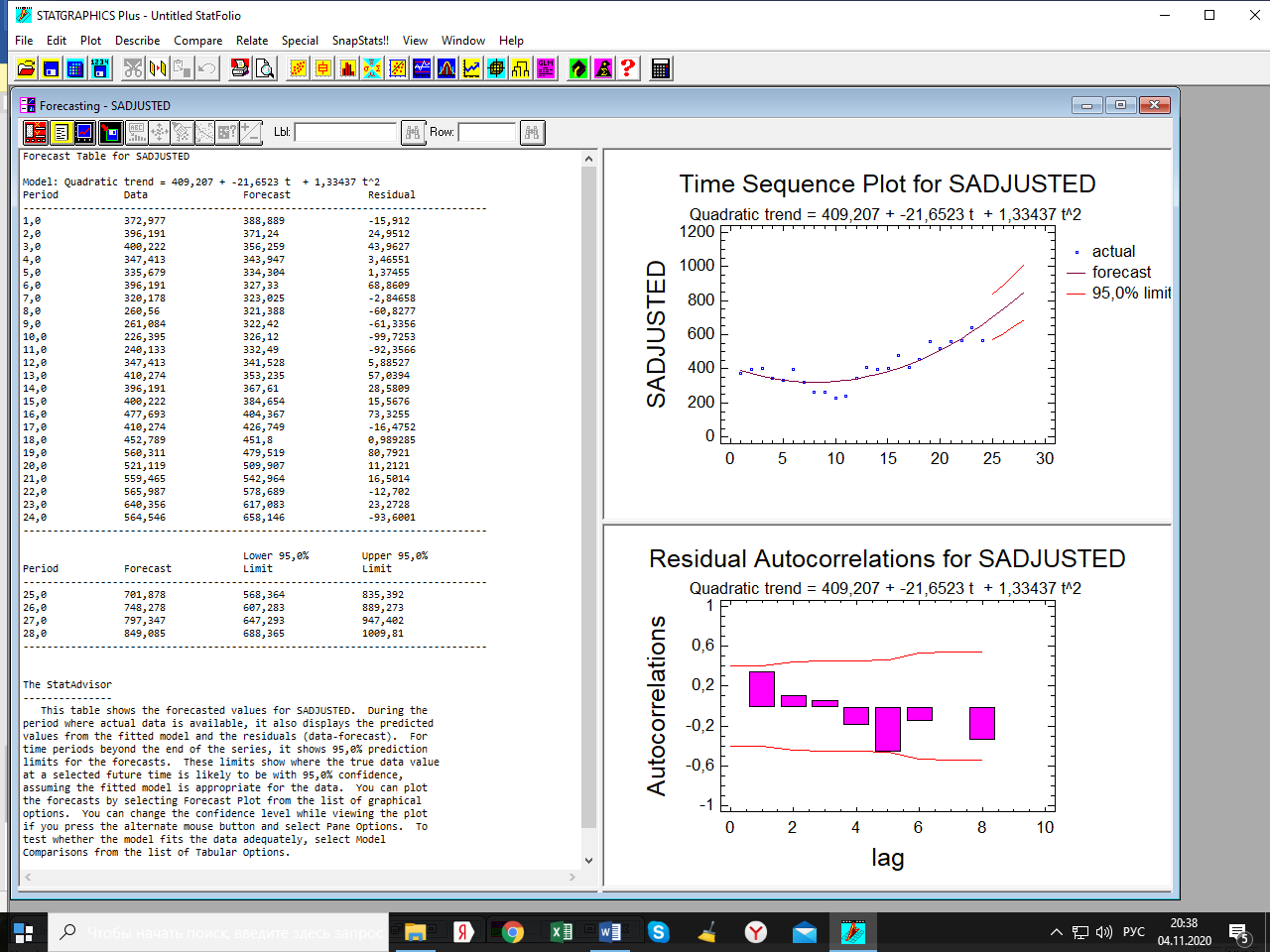 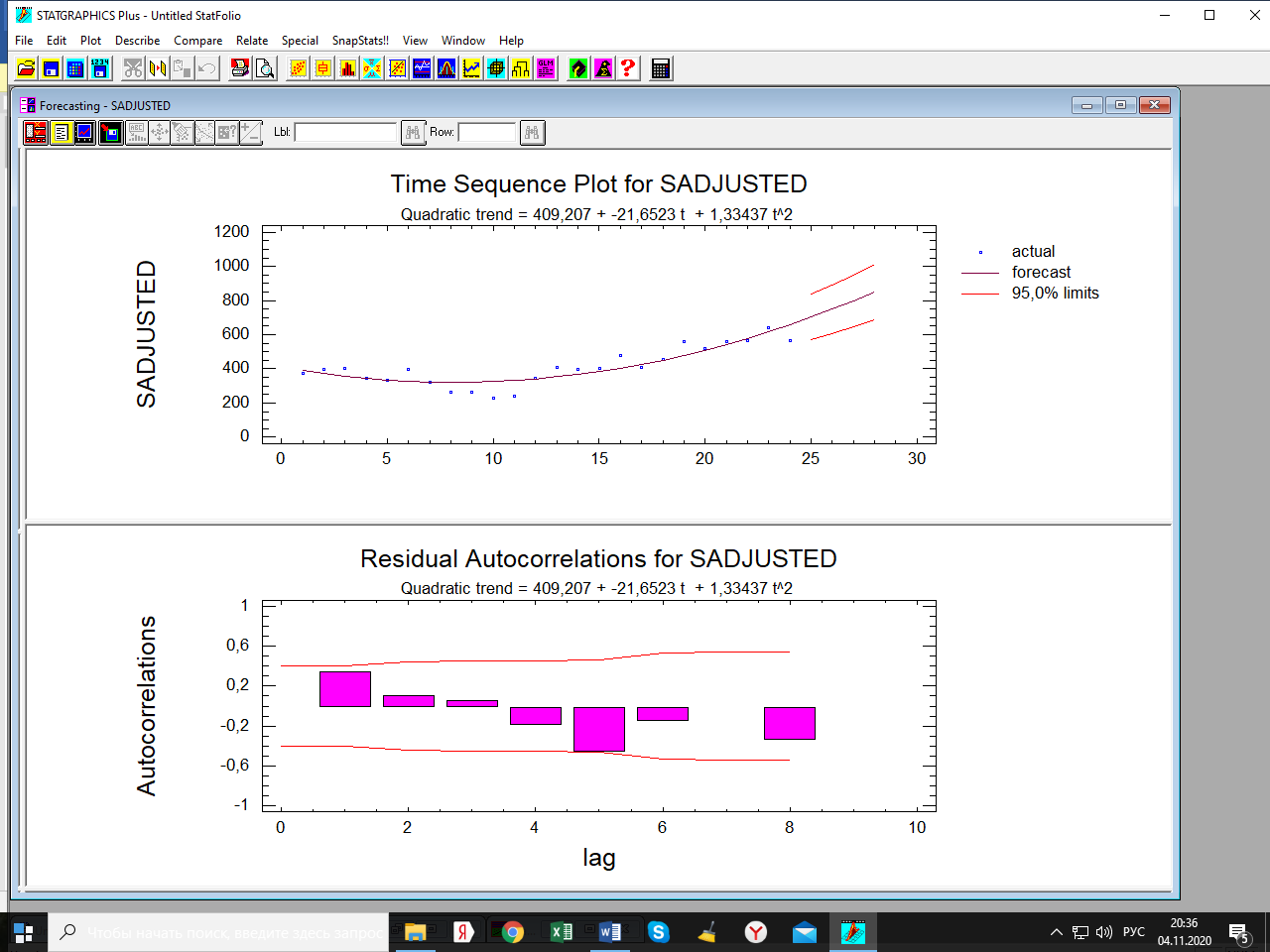 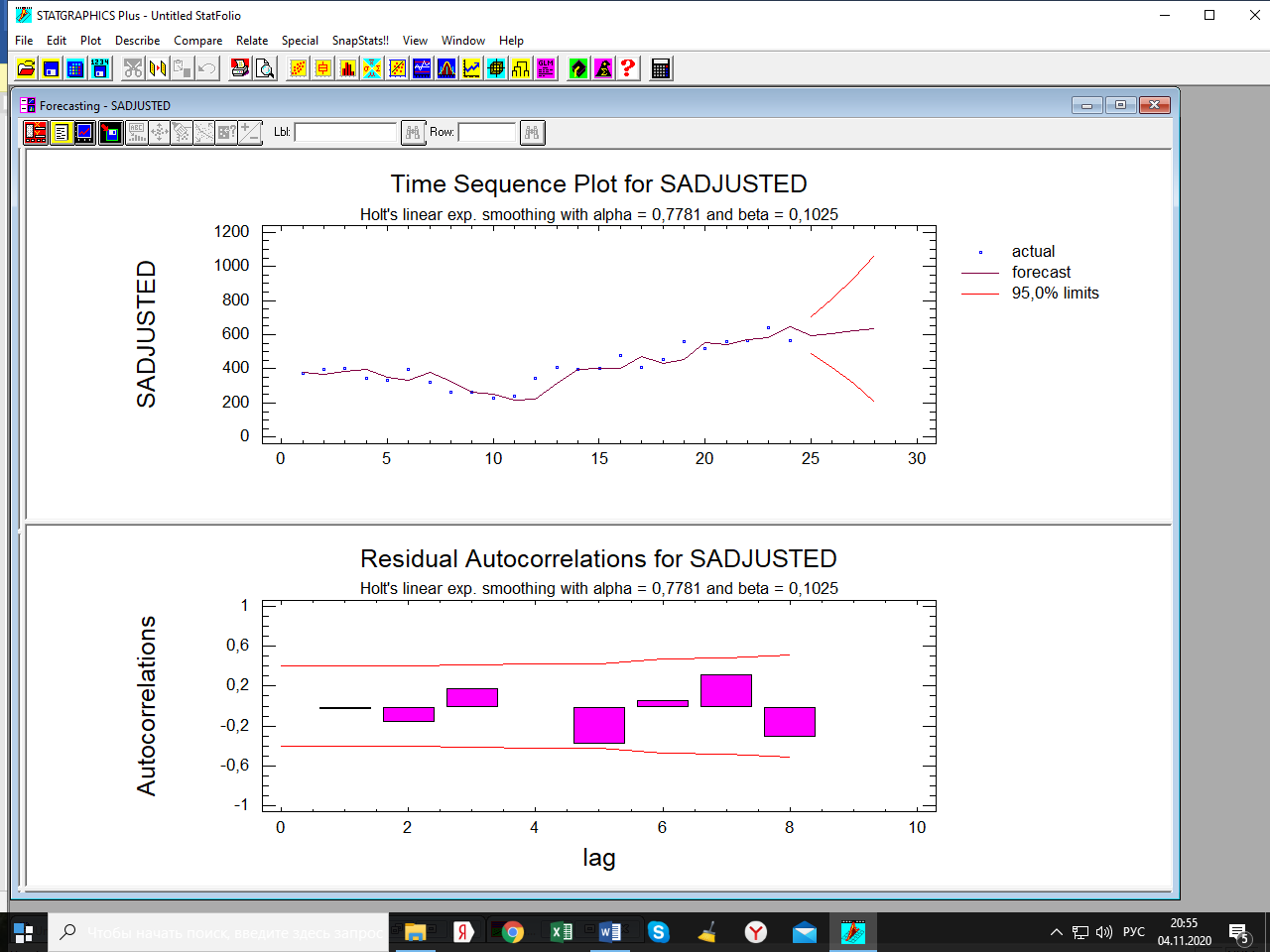 Прогноз по Хольту: 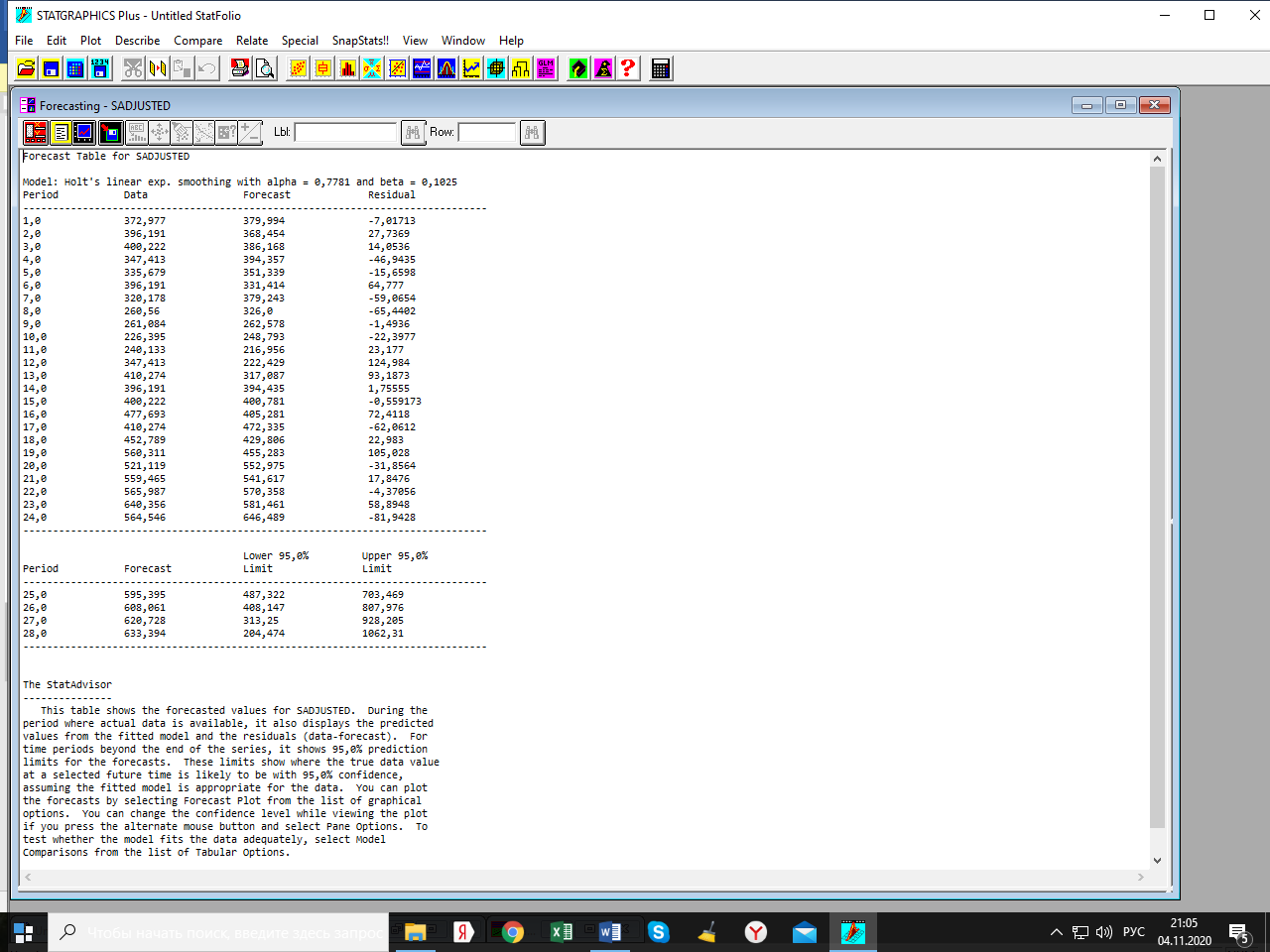 Так, например, прогноз по квадратичному тренду получился слишком оптимистичным. А по Хольта линейной модели (нижний график) – более осторожный и в большей мере соответствует реальным данным. Да и автокорреляционная функция иллюстрирует остатки, более близкими к «белому шуму». Пояснить. Прогноз получили по тренду. Теперь надо его подкорректировать с учётом сезонности, умножив каждое прогнозное значение на соответствующий индекс сезонности. Проделать самостоятельно с указанием доверительных границ. Адаптивные методы прогнозирования (экспоненциально взвешенные средние) Рассмотрим более подробно применение экспоненциально взвешенных средних к прогнозу временных рядов (теорию см. в уч. пособии). Пусть имеется след. вр. ряд (на рис. показан горизонтальный график ряда и его коррелограма). 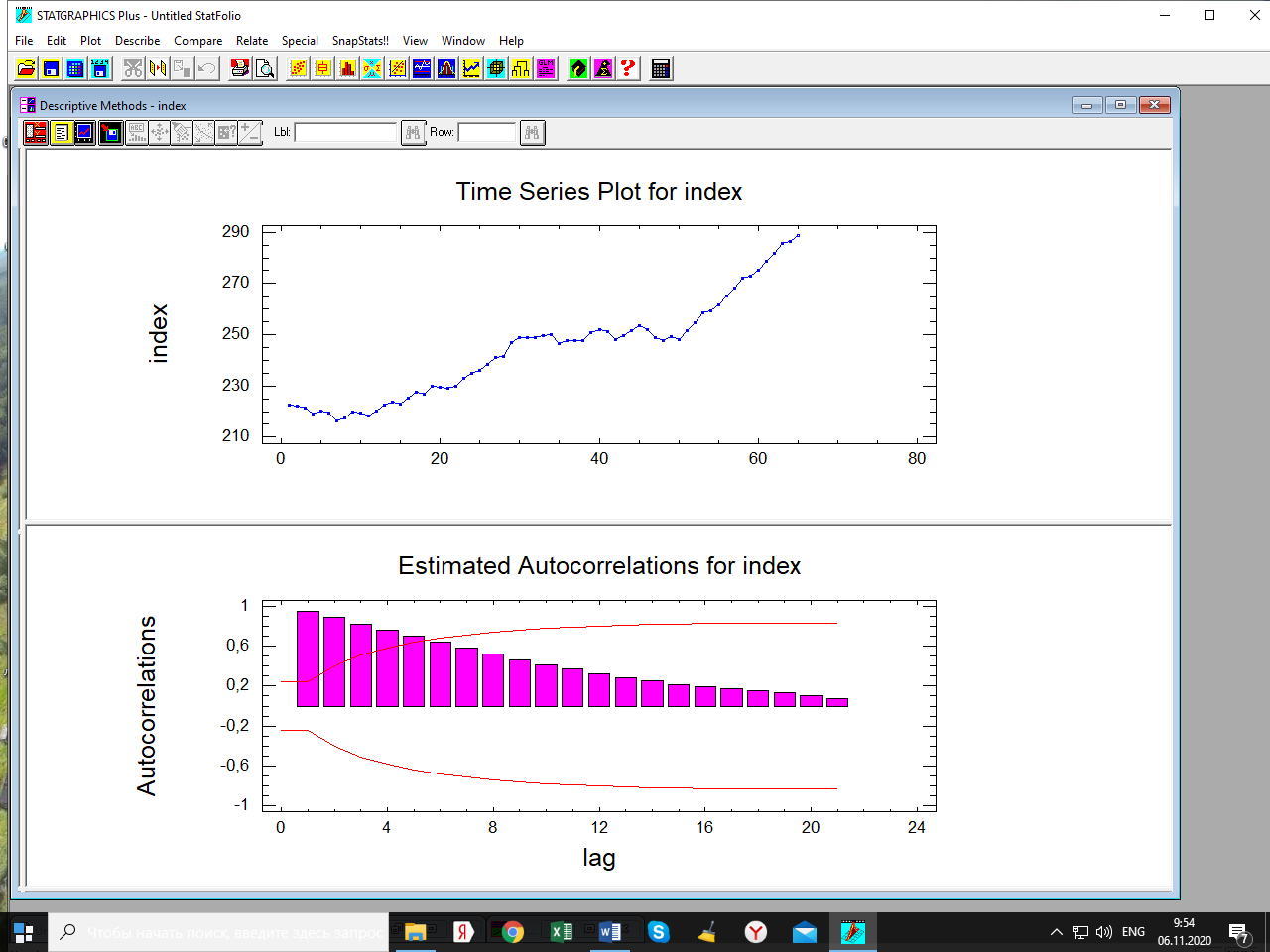 Коррелограма представляет собой типичную картину, когда временной ряд имеет только трендовую и случайную компоненты, что видно и из графика. Выберем наилучшую модель из представленных на рис. ниже по показателям точности прогноза. RMSE и MAE указывают на две модели: С и Е, т. е. на Хольта линейную и Брауна линейную. 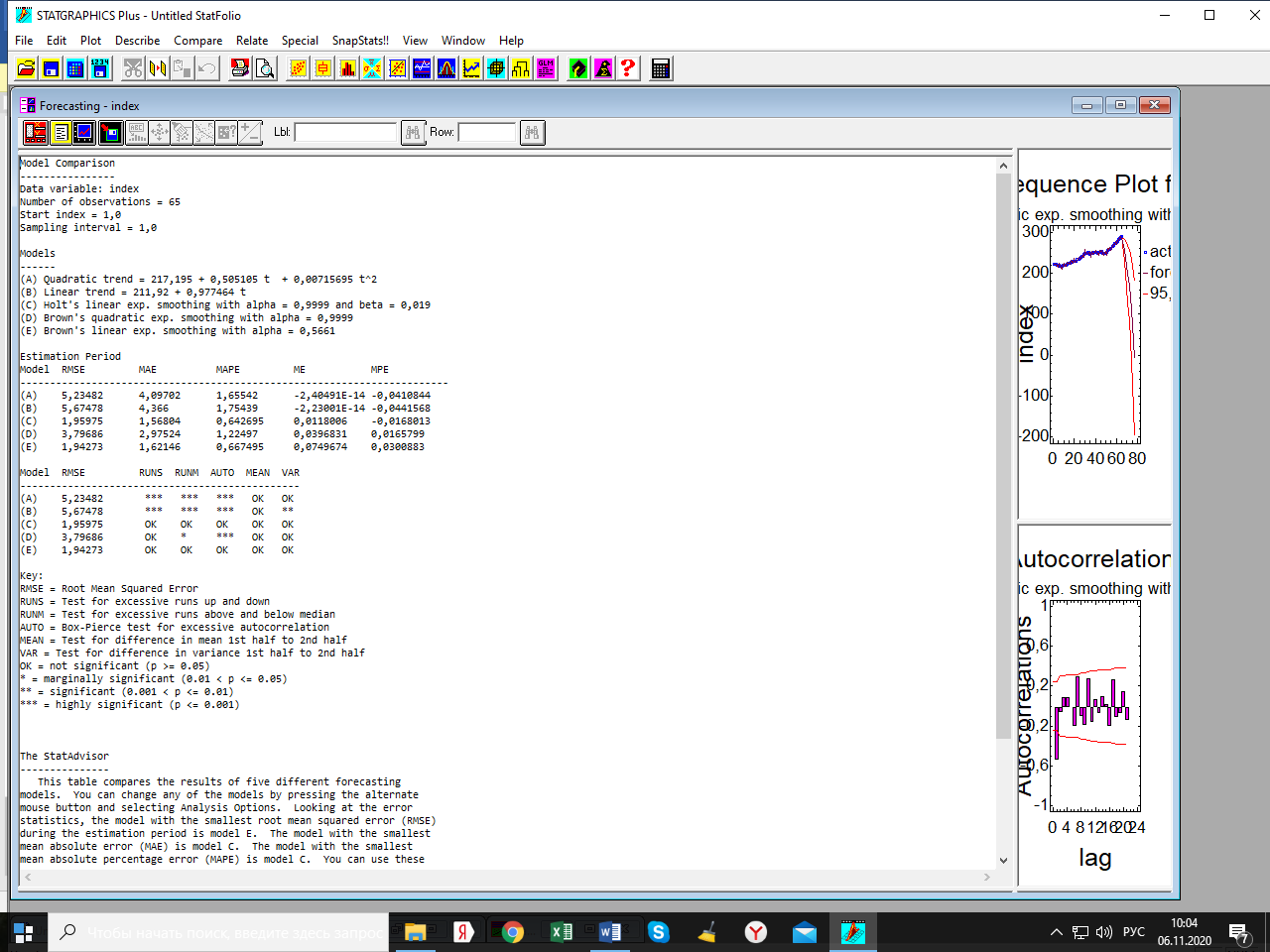 Посмотрим, какая из них лучше подходит для прогноза. Ниже представлены графики прогноза и коррелограмы остатков по обеим моделям. 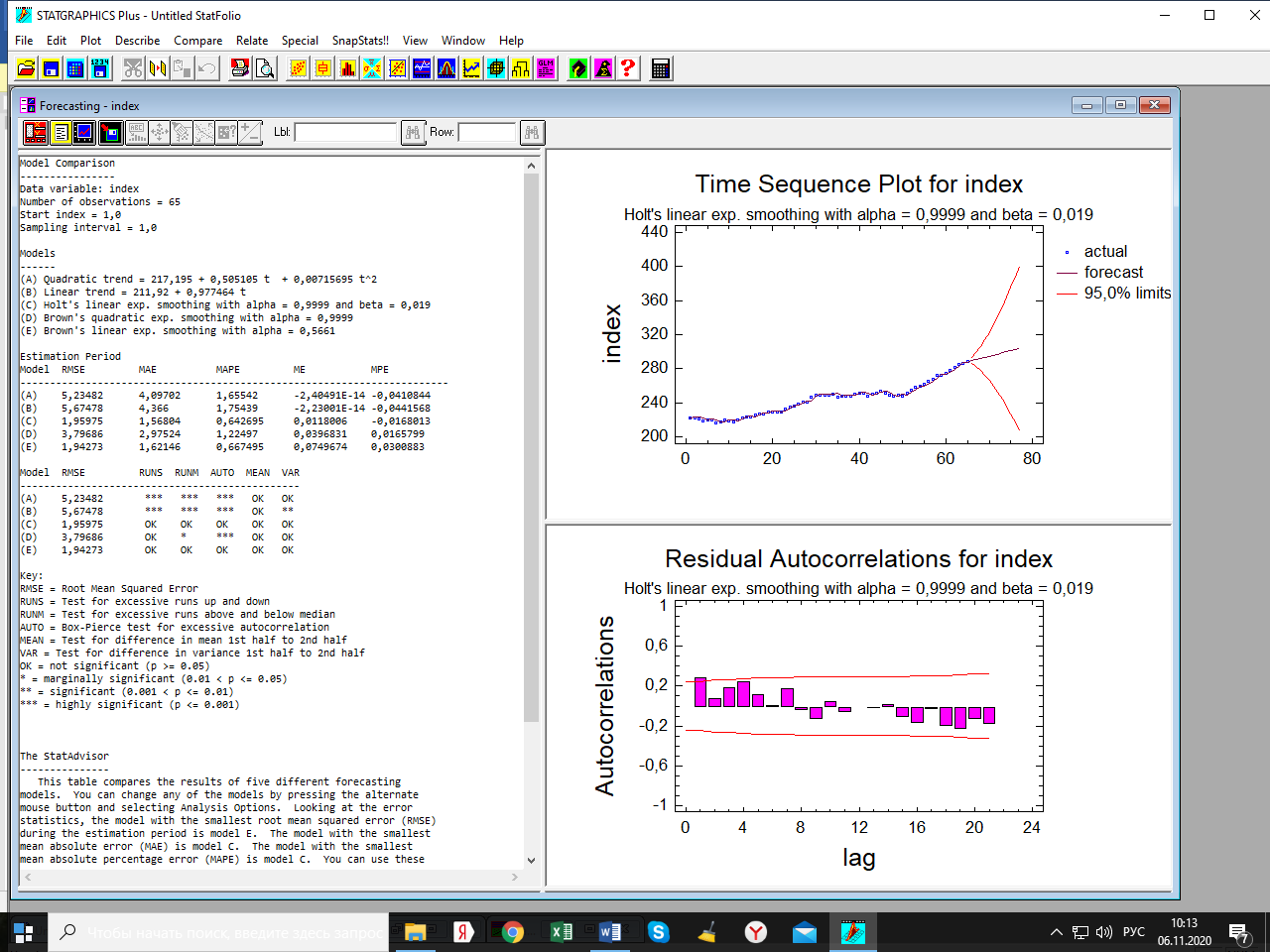 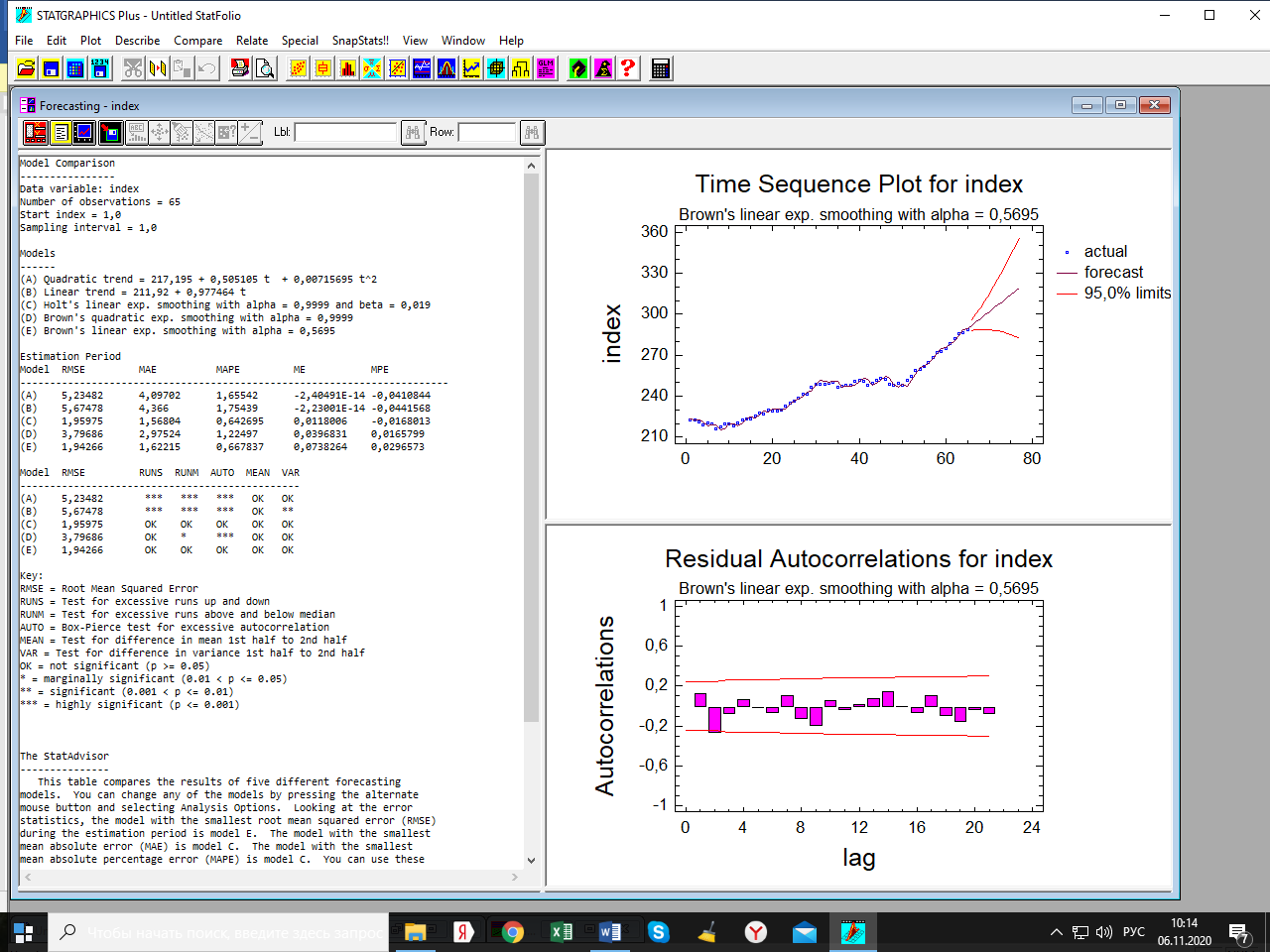 Обе коррелограмы указывают на то, что остатки моделей не являются «белым шумом» - автокорреляции выходят за пределы доверительной области нуля (особенно у модели Хольта). Да и размах доверительных границ по этой модели шире. Но зато у неё прогноз менее оптимистичен, чем по модели Брауна. Какую модель выбрать – решает исследователь. Ниже приведены прогнозы по обеим моделям на 6 периодов. 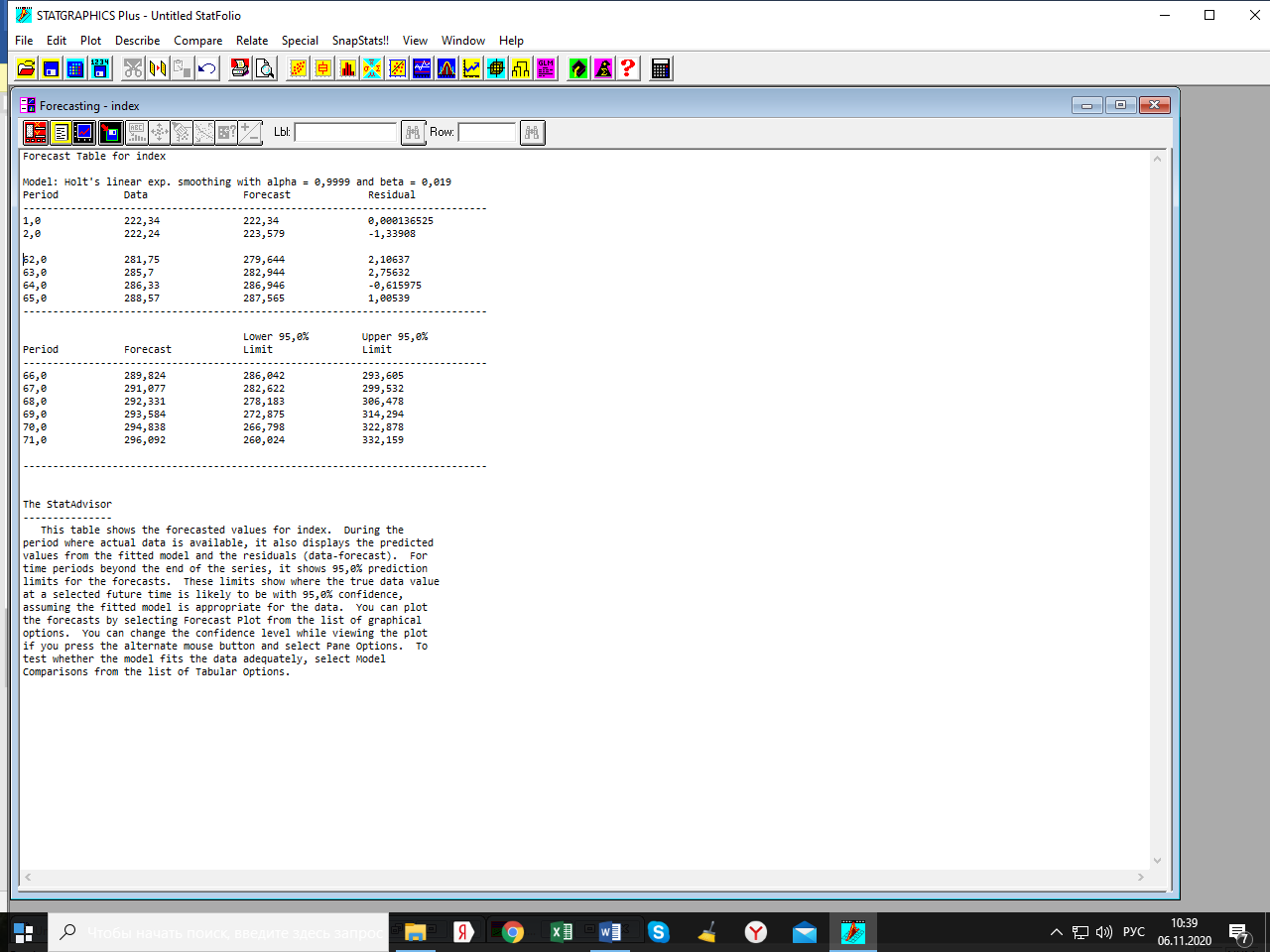 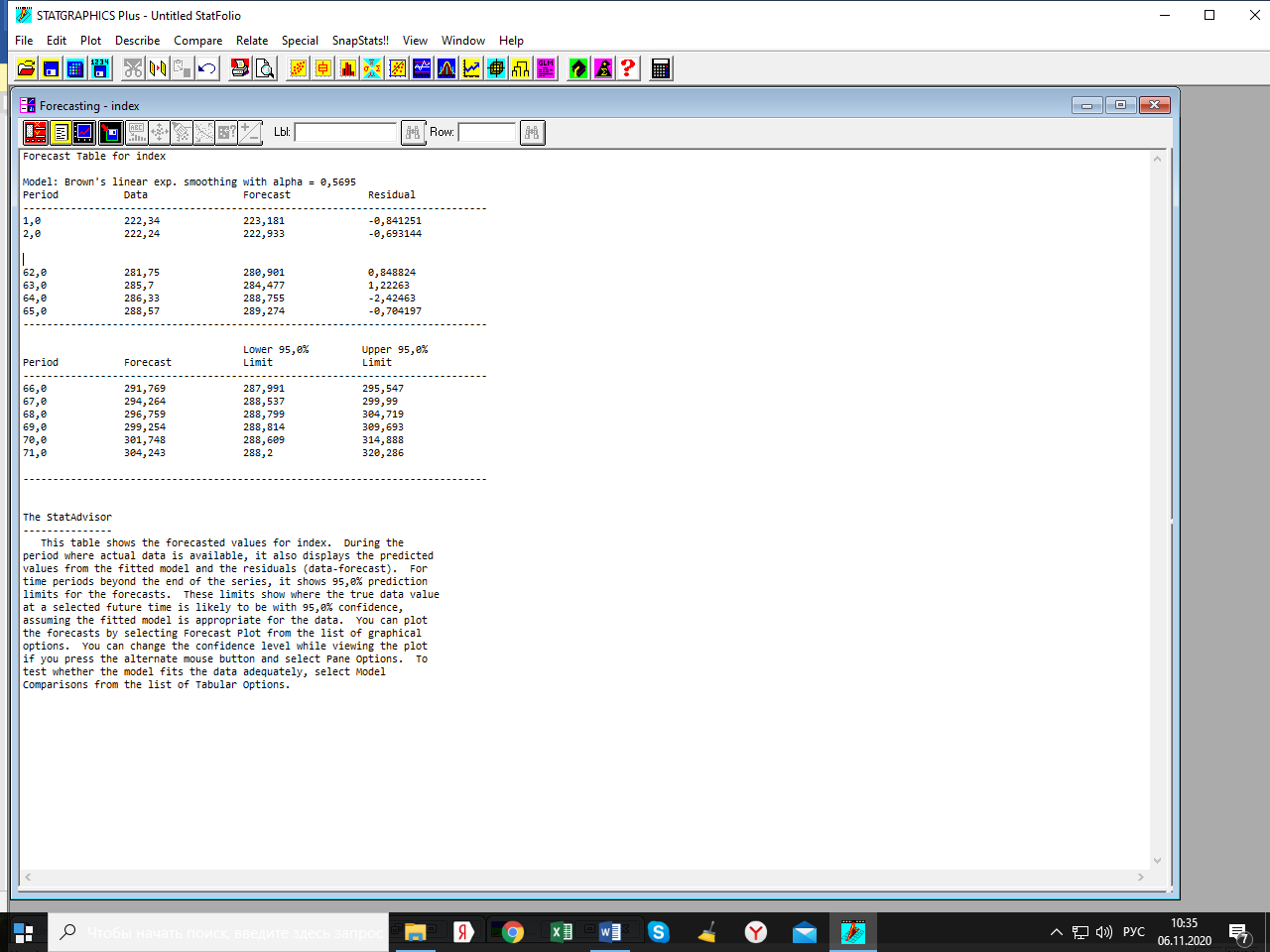 Как видим, по модели Брауна прогноз более оптимистичный. Следует иметь в виду, что прогнозирование – процесс творческий и здесь кроме формальных статистических критериев (показатели точности прогноза, поведение остатков и пр.) надо учитывать и не формальные критерии, согласующиеся с интересами аналитика. В заключение этой темы проиллюстрируем «работу» модели Винтера на ранее рассмотренном примере с сезонной составляющей. На рис. приведены прогноз и график автокорреляционной функции остатков по этой модели. 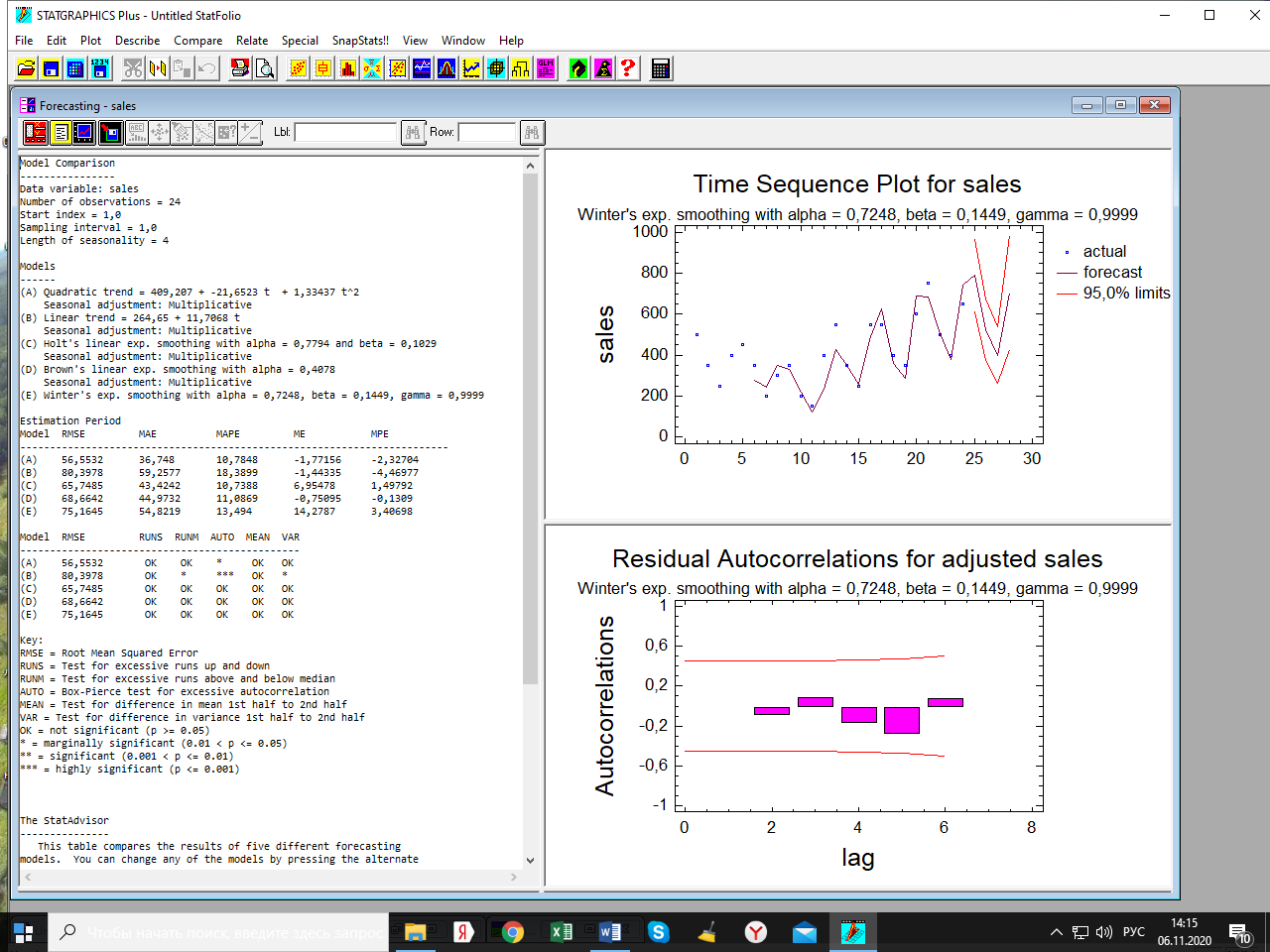 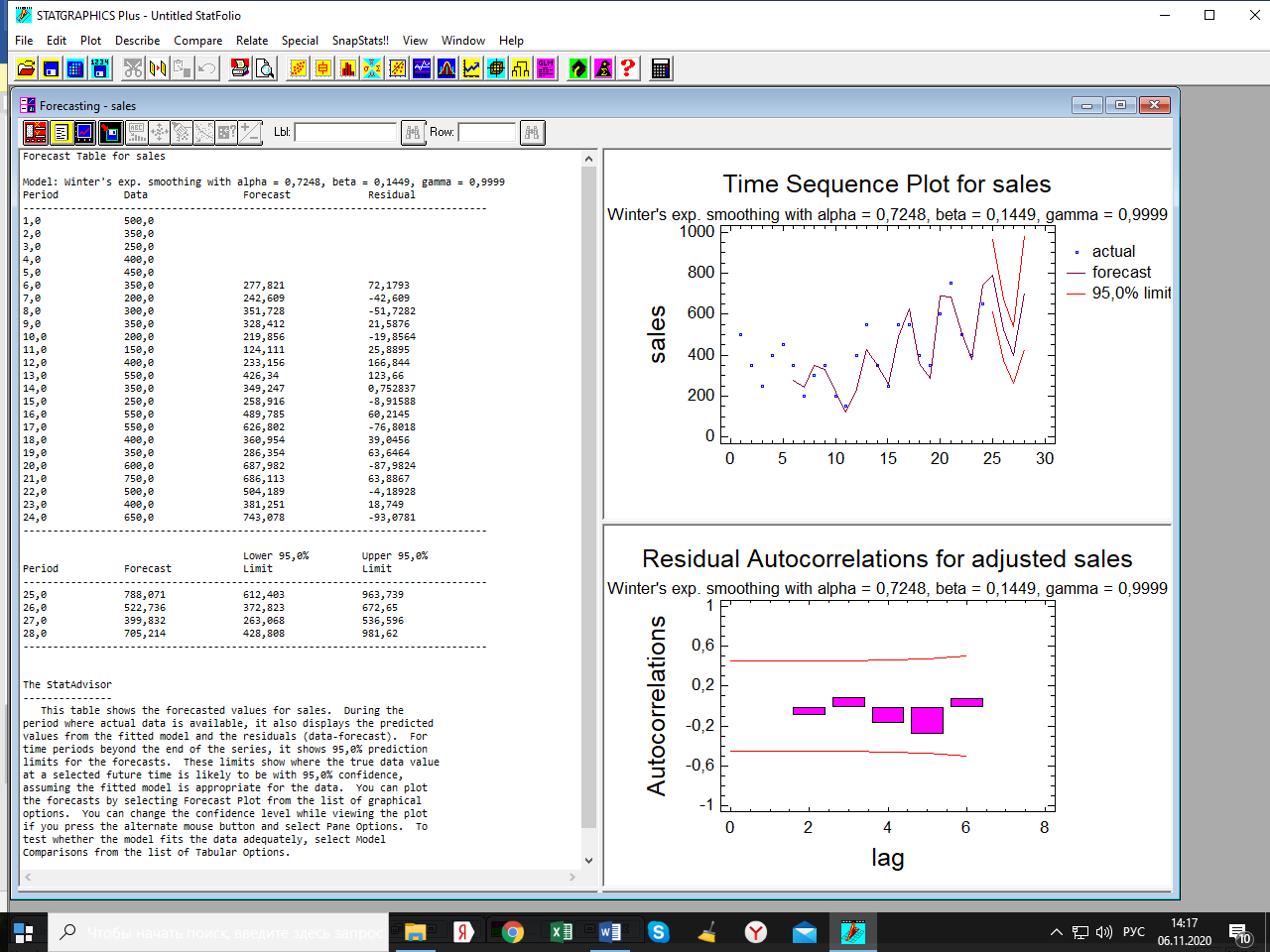 Здесь приведены данные за последний квартал исходных данных и прогноз на очередной квартал уже с учётом сезонности (сравните с прогнозом по методу сезонной декомпозиции). |
