ЛЕКЦИЯ №
Э Л Е М Е Н Т Ы К В А Н Т О В О Й М Е Х А Н И К И.
ВОЛНЫ ДЕ БРОЙЛЯ
Применение модели строения атомов, предложенной в 1913 году Н. Бором (датч.), к многоэлектронным атомам, показало, что эта теория несостоятельна и требуется новый, отличный от законов классической механики подход к изучению условий движения электронов в атоме. Первый шаг в этом направлении сделал в 1924 году французский физик Луи де Бройль. Развивая принцип корпускулярно-волнового дуализма, де Бройль утверждал: не только фотоны, но и любые другие частицы материи, в том числе и электроны, наряду с корпускулярными обладают также и волновыми свойствами.
Т.о. согласно де Бройлю с каждым микрообъектом связываются, с одной стороны, корпускулярные характеристики (энергия ε и импульс р), а с другой – волновые параметры (частота νБ и длина волны λБ). Количественные соотношения, связывающие эти величины, такие же, как и для фотонов:
ε = hνБ , р = 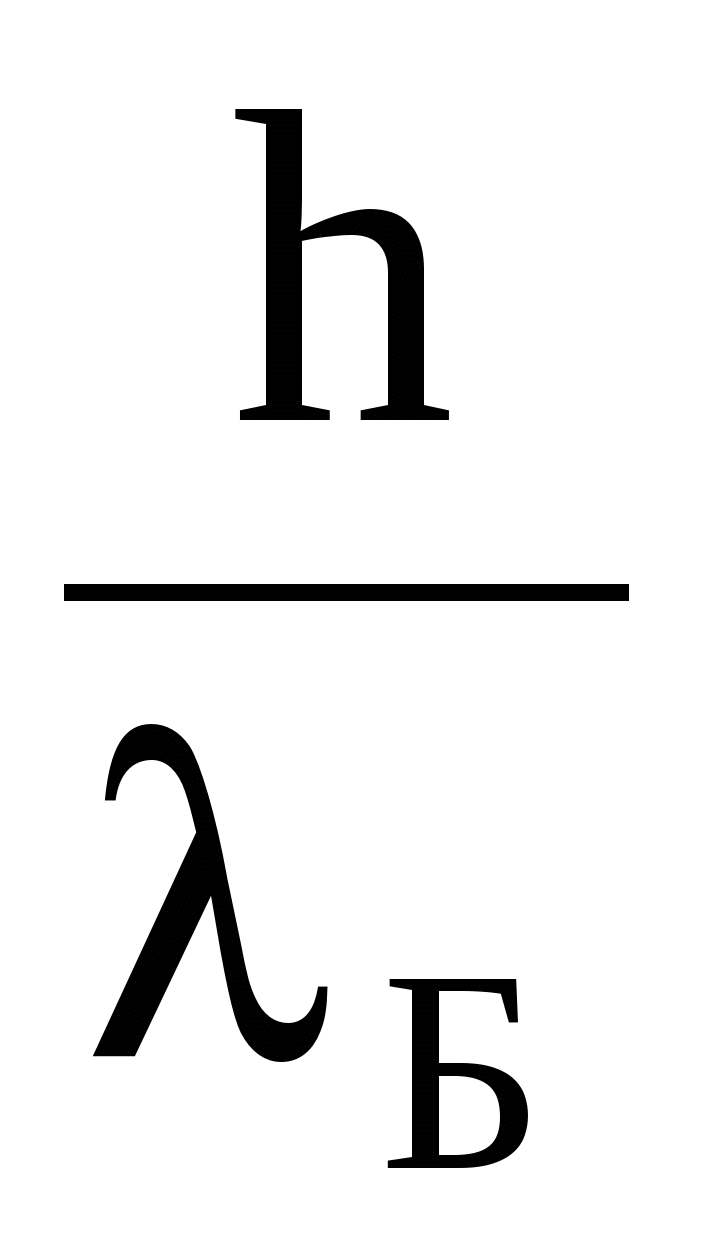 . (1) . (1)
Т.о. любой частице, обладающей импульсом р = mυ, соответствует волновой процесс с длиной волны
 . (2) . (2)
Найдём зависимость дебройлевской длины волны электрона ускоренного электрическим полем от величины ускоряющего напряжения U. Изменение кинетической энергии электрона равно работе электростатических сил:
 (3) (3)
Выразим отсюда скорость υ и подставим в (2), получим:
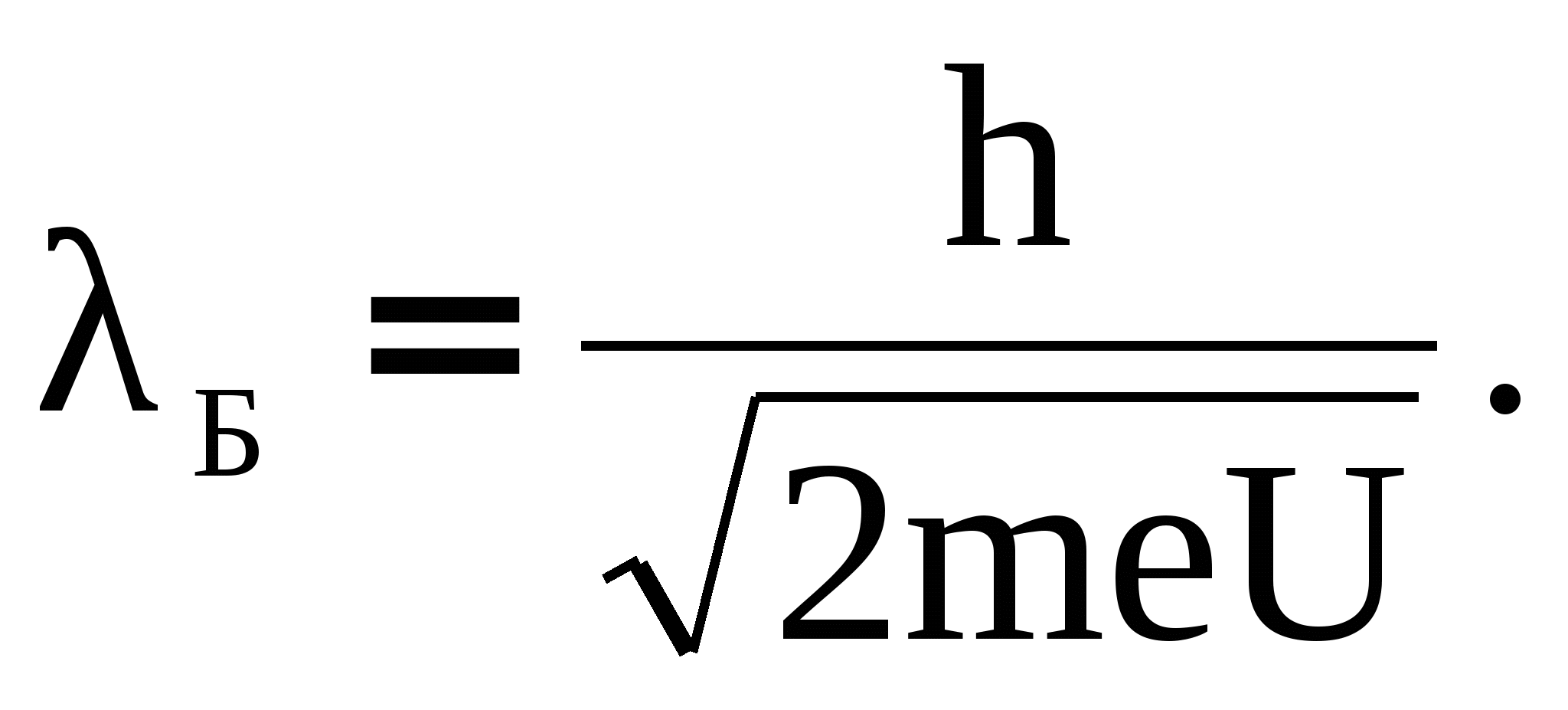 (4) (4)
Например, электронам ускоренным электрическим полем с разностью потенциалов от 1 до 104 В, что имеет место в электровакуумных приборах (электроннолучевая трубка), соответствуют дебройлевские длины волн от 1 до 0,01 нм. По шкале электромагнитных волн это диапазон рентгеновского излучения. Следовательно, если пучок таких электронов направить на кристалл, то он должен дифрагировать подобно рентгеновскому излучению. И действительно, проверяя гипотезу де Бройля, в 1927 году американские физики К. Девиссон и Л. Джермер направили на кристалл никеля пучок электронов, который после рассеяния дал четкую дифракционную картину (рис.1а). Расчет длины волны по положениям дифракционных максимумов дал значение, совпадающее с длинной волны, вычисленной по формуле (2). На рис 1б приведена полученная в аналогичных условиях рентгенограмма. Сходство обеих картин очевидно.
Следует иметь ввиду, что волны де Бройля не связаны с каким-либо колебательным процессом. Они только лишь характеризуют волновые свойства движущихся частиц, в том числе и макроскопических тел. Однако для тел большой массы длина волны де Бройля настолько мала, что ее невозможно обнаружить никакими современными приборами.
О ткрытие волновых свойств микрочастиц привело к появлению новых исследовательских физических методов. Аналогично рентгеноструктурному анализу дифракцию частиц можно использовать для оценки степени упорядоченности в расположении атомов и молекул в веществе, также для измерения параметров кристаллической решётки. В настоящее время широкое распространение имеют электронография (основана на дифракции электронов) и нейтронография (дифракция нейтронов). ткрытие волновых свойств микрочастиц привело к появлению новых исследовательских физических методов. Аналогично рентгеноструктурному анализу дифракцию частиц можно использовать для оценки степени упорядоченности в расположении атомов и молекул в веществе, также для измерения параметров кристаллической решётки. В настоящее время широкое распространение имеют электронография (основана на дифракции электронов) и нейтронография (дифракция нейтронов).
Методы электронографии широко используются при исследовании структуры поверхностей, процессов коррозии, адсорбции газов и ряда других поверхностных явлений. Это связано с тем, что наличие заряда у электронов вызывает их сильное взаимодействие с электронными оболочками атомов вещества и как следствие рассеяние электронов атомами поверхностного слоя исследуемого тела.
Нейтронография оказывается особенно полезной при изучении структур содержащих водород, в частности органических веществ. Объясняется это тем, что нейтроны сильно поглощаются атомами водорода, в то время как электроны и рентгеновские лучи слабо взаимодействуют с водородосодержащими молекулами.
ЭЛЕКТРОННЫЙ МИКРОСКОП. ПОНЯТИЕ ОБ ЭЛЕКТРОННОЙ ОПТИКЕ
Волновые свойства частиц можно использовать не только для структурного дифракционного анализа, но и для получения увеличенных изображений предмета.
Предел разрешения оптического микроскопа (Лк. №11, ) определяется в основном наименьшим значением длины волны света, воспринимаемого глазом человека. Подставив в эту формулу значение длины волны де Бройля (4), найдем предел разрешения электронного микроскопа, в котором изображение предмета формируется электронными пучками:
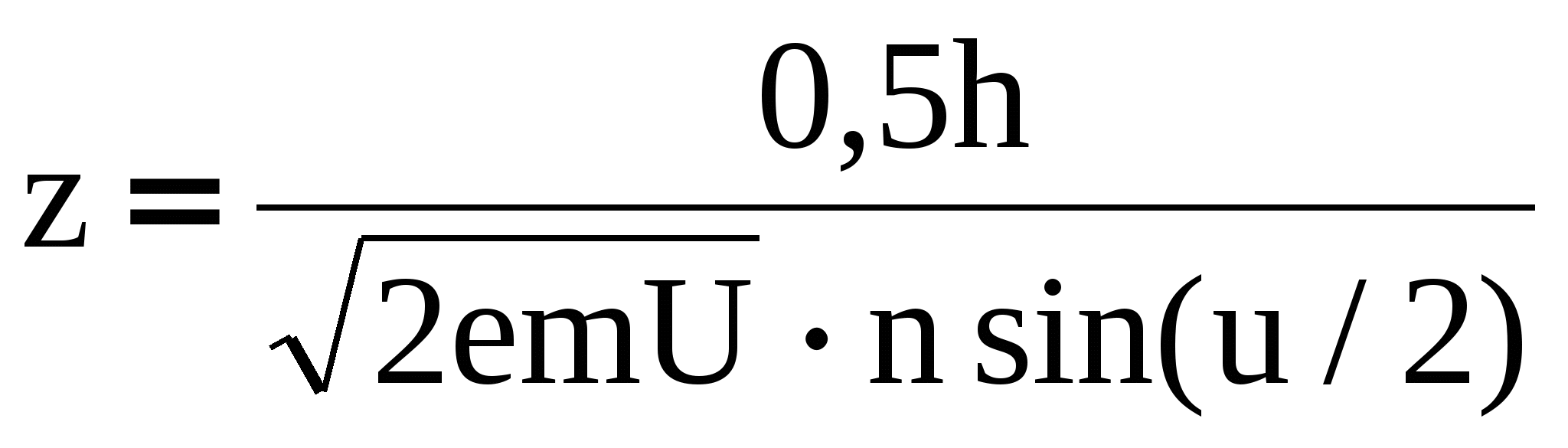 , (5) , (5)
где h – постоянная Планка; е и m – заряд и масса электрона; U – ускоряющее напряжение; n – показатель преломления среды; u – апертурный угол. Из (5) видно, что предел разрешения z электронного микроскопа зависит от ускоряющего напряжения U, увеличивая которое можно добиться, чтобы предел разрешения был значительно меньше, а разрешающая способность значительно больше, чем у оптического микроскопа. Электронный микроскоп и его отдельные элементы по своему назначению подобны оптическому (рис. 2).
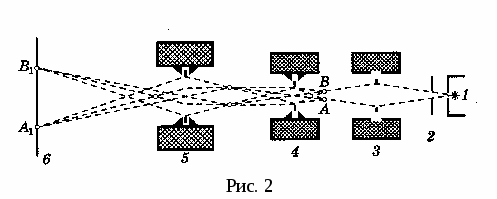
В электронном микроскопе носителем информации об образце являются электроны, а их источником — подогреваемый катод 1. Ускорение электронов и образование пучка осуществляется фокусирующим электродом и анодом — системой, называемой электронной пушкой 2. После взаимодействия с образцом (в основном рассеяние) поток электронов преобразуется и содержит информацию об образце. Формирование потока электронов происходит под воздействием электрического (система электродов и конденсаторов) и магнитного (система катушек с током) полей. Эти системы называют электронными линзами по аналогии с оптическими линзами, которые формируют световой поток (3 – конденсорная; 4 – электронная, служащая объективом; 5 – проекционная). Изображение регистрируется на чувствительной к электронам фотопластинке или катодолюминесцирующем экране 6.
Чтобы оценить предел разрешения электронного микроскопа, подставим в формулу (4) ускоряющее напряжение U = 100 кВ и угловую апертуру u 10-2 рад (приблизительно такие углы используют в электронной микроскопии). Получим z 0,1 нм; это в сотни раз лучше, чем у оптических микроскопов. Применение ускоряющего напряжения, большего 100 кВ, хотя и повышает разрешающую способность, но сопряжено с техническими сложностями, в частности происходит разрушение исследуемого объекта электронами, имеющими большую скорость. Для биологических тканей из-за проблем, связанных с приготовлением образца, а также с его возможным радиационным повреждением, предел разрешения составляет около 2 нм. Этого достаточно, чтобы увидеть отдельные молекулы.
Укажем некоторые особенности эксплуатации электронного микроскопа. В тех его частях, где пролетают электроны, должен быть вакуум, так как в противном случае столкновение электронов с молекулами воздуха (газа) приведет к искажению изображения. Это требование к электронной микроскопии усложняет процедуру исследования, делает аппаратуру более громоздкой и дорогой. Вакуум искажает некоторые свойства биологических объектов, а в ряде случаев разрушает или деформирует их.
В качестве препаратов в электронной микроскопии используются очень тонкие срезы (толщина менее 0,1 мкм) биообъектов, так как электроны сильно поглощаются и рассеиваются веществом.
Для исследования поверхностной геометрической структуры клеток, вирусов и других микрообъектов делают отпечаток (реплику) их поверхности на тонком слое пластмассы. Обычно предварительно на реплику в вакууме напыляют под скользящим (малым к поверхности) углом слой сильно рассеивающего электроны тяжелого металла (например, платины), оттеняющий выступы и впадины геометрического рельефа.
К достоинствам электронного микроскопа следует отнести большую разрешающую способность, позволяющую рассматривать крупные молекулы, возможность изменять при необходимости ускоряющее напряжение и, следовательно, предел разрешения, а также сравнительно удобное управление потоком электронов с помощью магнитных и электрических полей.
Электронные микроскопы позволяют получить увеличение порядка 105 - 106, а их предел разрешения в сравнении с оптическим микроскопом в сотни раз меньше.
СООТНОШЕНИЕ НЕОПРЕДЕЛЁННОСТЕЙ
Обнаружение волновых свойств микрочастиц означает, что классическая механика не может дать правильного описания поведения микрообъектов. Новая физическая теория, устанавливающая законы движения и взаимодействия микрочастиц и фотонов с учетом их волновых и корпускулярных свойств, была разработана, главным образом, тремя физиками: Э. Шредингером (австр.), В. Гейзенбергом (нем.) и П. Дираком (англ.) в начале ХХ века и получила название волновой или квантовой механики.
В классической механике всякая частица движется по определённой траектории, так что ее координаты и импульс могут быть точно рассчитаны для любого момента времени. Совсем по иному обстоит дело, если рассматривается вопрос о локализации волнового процесса, т.е. о месте нахождения волны в данный момент времени. Ведь волна не имеет ни определенной траектории, ни определенной координаты. Т.о. возникает необходимость внести некоторые ограничения в применении к объектам микромира понятий классической механики.
Эти ограничения сформулированы Гейзенбергом и получили название соотношений неопределенностей. Основное из них гласит: чем точнее определены какие-либо из координат частицы, тем больше неопределенность в значении составляющей импульса (или скорости) в том же направлении, и наоборот. Количественно это записывается так:
Δx·Δpx ≥ ђ Δx·Δυx ≥ ђ/m,
Δy·Δpy ≥ ђ Δy·Δυy ≥ ђ/m, (3)
Δz·Δpz ≥ ђ Δz·Δυ z ≥ ђ/m,
где Δx, Δy, Δz – неопределенности координат; Δpx, Δpy, Δpz – неопределенности проекций импульса на оси – x, y, z; Δυx, Δυy , Δυz – неопределенности проекций скоростей на соответствующие оси; m – масса микрочастицы; ђ = h/2π – постоянная Планка с крышечкой.
Из соотношения неопределенностей следует: если положение частицы точно известно (Δx=0), то в этом состоянии проекция импульса на ось х-ов совершенно не определена (Δpх→ ∞), и наоборот.
Покажем, что соотношение неопределенностей действительно вытекает из волновых свойств микрочастиц. Рассмотрим мысленный опыт по дифракции потока электронов на щели шириной Δx λ, расположенной перпендикулярно к направлению движения частиц (рис. 3).
Д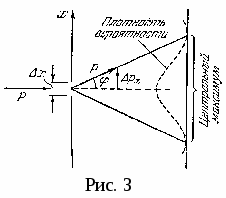 о прохождения через щель pх = 0; ∆pх = 0, а координата x не определена, т.е. ∆x→ ∞. В момент прохождения через щель координата электрона имеет неопределенность ∆x равную ширине щели. В то же время, из-за дифракции, электроны отклоняются от первоначального направления и будут двигаться в пределах угла 2φ, где φ – угол дифракции. Теперь появляется неопределенность в значении составляющей импульса вдоль оси x-ов: о прохождения через щель pх = 0; ∆pх = 0, а координата x не определена, т.е. ∆x→ ∞. В момент прохождения через щель координата электрона имеет неопределенность ∆x равную ширине щели. В то же время, из-за дифракции, электроны отклоняются от первоначального направления и будут двигаться в пределах угла 2φ, где φ – угол дифракции. Теперь появляется неопределенность в значении составляющей импульса вдоль оси x-ов:
∆pх = p∙sinφ = h sinφ / λБ . (4)
Если даже ограничиться электронами, попадающими на экран в пределах центрального максимума, то sinφ найдем из условия 1-ого минимума на щели (bsinφ = kλ, где b – ширина щели, k – порядок минимума):
∆x∙sinφ = λБ. (5)
Подставляя выражение для sinφ в (4), после преобразования получим
Δx·Δpx = h (6)
Учитывая главные max более высоких порядков, куда тоже попадают электроны, окончательно будем иметь:
Δx·Δpx ≥ h ≥ ђ (7)
Следует подчеркнуть, что невозможность одновременного и точного определения координаты и соответствующей составляющей импульса не связана с несовершенством наших знаний или неточностью приборов, а является следствием специфических и вместе с тем объективных свойств микрообъектов.
Проиллюстрируем оценку границ применимости теории на примерах.
Скорость движения электрона в электроннолучевой трубке составляет υх=106 м/с и определена с точностью до Δυх=102 м/с. Тогда неопределенность координаты:
Δx·Δυx ≥ ђ/m, 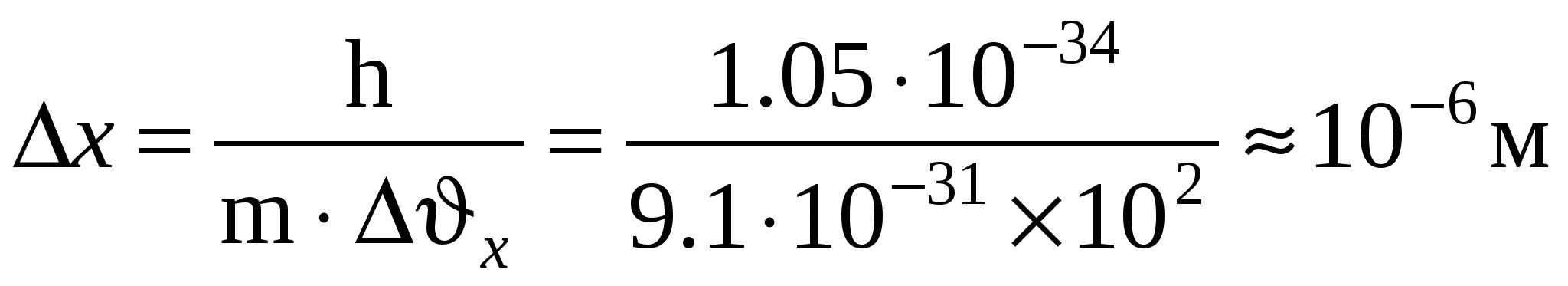 . . 
Т.е. в данном случае можно говорить о точке падения каждого отдельного электрона на экран и о траектории.
Скорость движения электрона в атоме водорода υх 106 м/с, неопределенность координаты порядка диаметра атома Δx = d 10-10 м. Тогда неопределенность величины скорости
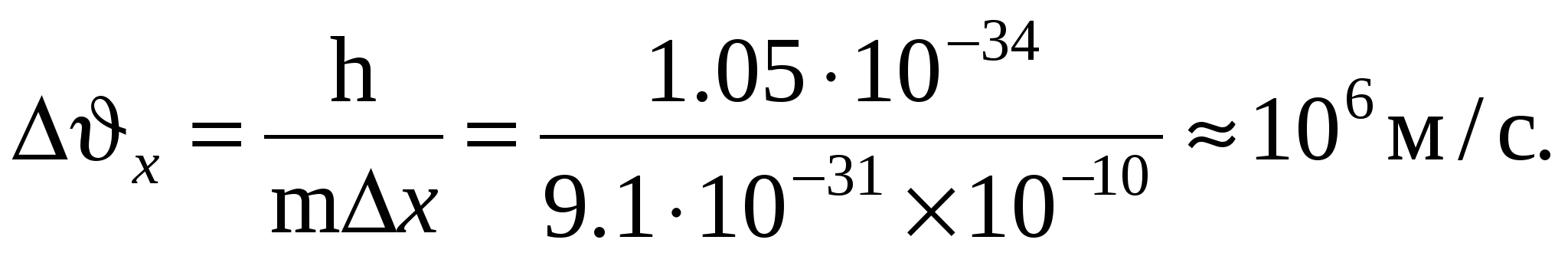
Т.е. неопределенность скорости соизмерима с самой скоростью. Это означает, что электрон не может теперь рассматриваться как дискретная частица.
Соотношение неопределенностей может быть записано для любой пары взаимосвязанных характеристик состояния микрочастиц, например, для энергии и времени пребывания в этом энергетическом состоянии:
ΔЕ·Δt ≥ ђ. (8)
Из данного соотношения видно, что разброс энергии ΔЕ = ђ/Δt возрастает с уменьшением среднего времени пребывания системы в состоянии с энергией Е. Отсюда, следует, что частота излученного фотона также должна иметь неопределенность:
Δv = ΔЕ / h, (9)
т.е. линии спектра, обусловленные переходом электронов между уровнями Е1 и Е2 с ΔЕ = Е1 – Е2, будут иметь размытие по частоте равное Δv= v0 ± ΔЕ / h, что подтверждается опытом.
ВОЛНОВАЯ ФУНКЦИЯ
Дифракционная картина, наблюдаемая для микрочастиц, характеризуется неодинаковым распределением рассеянных частиц по разным направлениям. С точки зрения волновой теории это означает, что направлениям максимумов соответствует наибольшая интенсивность волн де Бройля, а минимумам – наименьшая. Т.е. интенсивность волны де Бройля в данной точке пространства определяет число частиц, попавших в эту точку. Т.о. дифракционная картина для микрочастиц является проявлением статистической закономерности. Это означает, что описание поведения микрочастиц должно носить вероятностный характер, что и является важнейшей отличительной особенностью квантовой механики от классической. Состояние микрочастиц в квантовой механике описывается с помощью, так называемой, волновой функции вида ψ = f(x,y,z,t). Ее называют еще ψ-функция. Квадрат модуля ψ-функции определяет вероятность обнаружения частицы в момент времени t в области с координатами: x и x + dx; y и y + dy; z и z + dz – т.е. в элементе объема dV = dx dy dz: dW = | ψ |2 dV. (10)
Величина | ψ |2 = dW /dV – имеет смысл плотности вероятности, т.е. определяет вероятность нахождения частицы в единичном объеме в окрестностях точки с координатами x,y,z. Т.о. физический смысл имеет не сама ψ-функция, а квадрат её модуля – |ψ|2, которым и задается интенсивность волн де Бройля. Теперь вероятность найти частицу в момент времени t в объеме V будет:
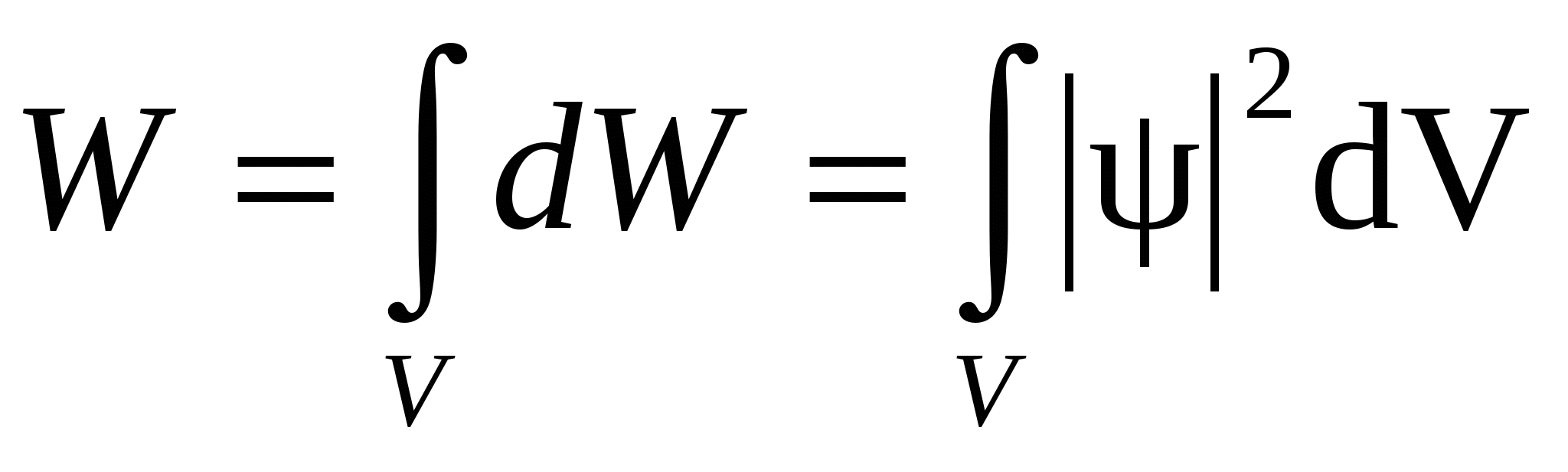 . (11) . (11)
Очевидно, что объективность существования частицы во времени и в пространстве будет выражаться вероятностью достоверного события:
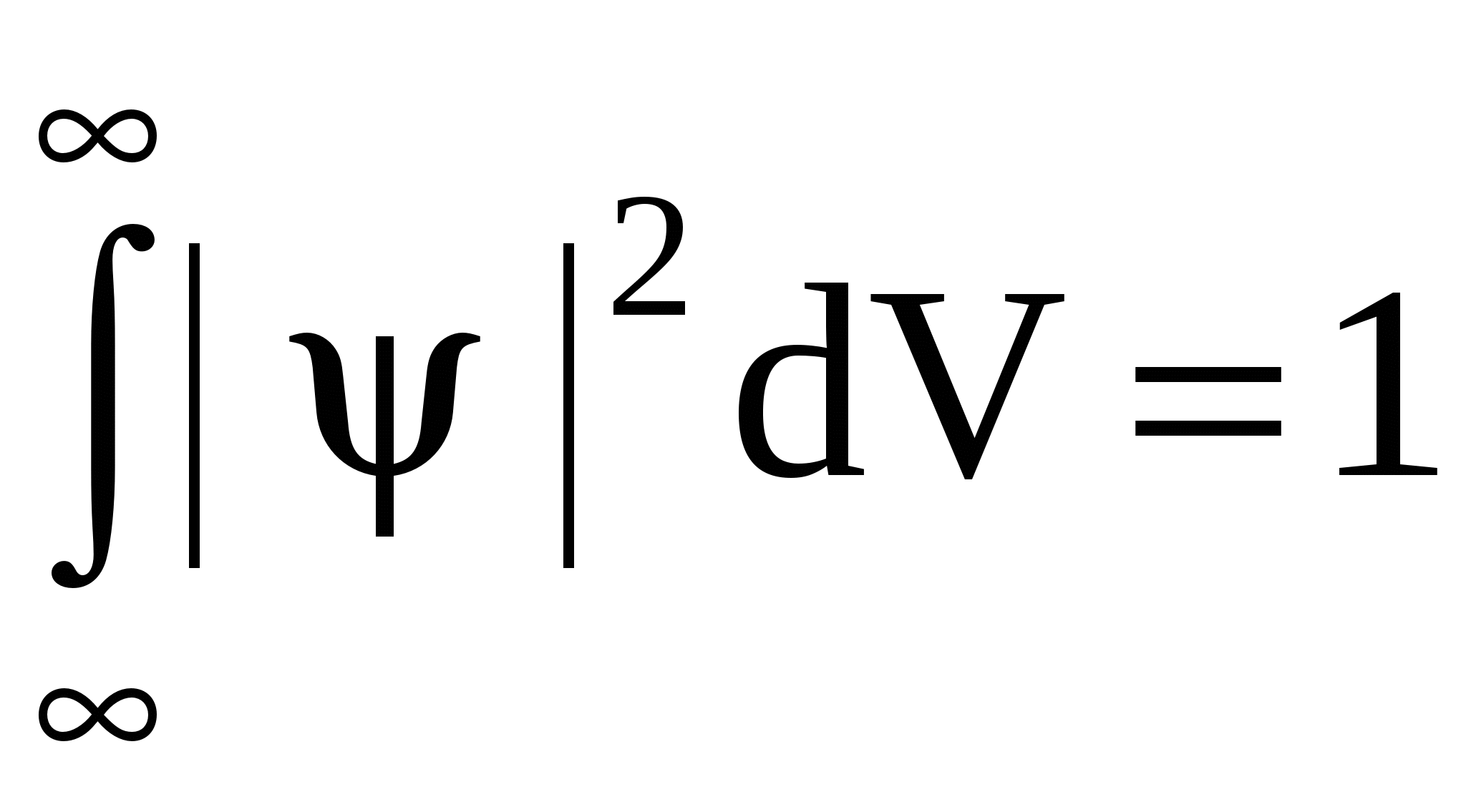 . (12) . (12)
Это соотношение является условием нормировки ψ- функции.
Волновая функция позволяет рассчитать вероятность реализации тех или иных значений параметров микрообъекта или их средние величины, например, расстояние электрона от ядра атома или вероятность перехода электрона с одного энергетического уровня на другой, что в свою очередь позволяет оценить относительную интенсивность спектральных линий.
Что бы ψ-функция являлась объективной характеристикой состояния микрочастицы она должна удовлетворять следующим условиям: быть 1) конечной, т.к. W ≤ 1; 2) однозначной, т.к. вероятность не может быть неоднозначной; 3) непрерывной, т.к. вероятность не может изменяться скачком.
УРАВНЕНИЕ ШРЕДИНГЕРА
В зависимости от конкретных условий волновая функция, как основной носитель информации о корпускулярных и волновых свойствах микрочастиц должна иметь разный вид. Соответственно, уравнение из которого определяется вид ψ-функции должно быть волновым, подобно дифференциальному волновому уравнению механических или электромагнитных волн. Такое уравнение составлено в 1926 году Э. Шредингером. В наиболее простом случае для стационарных режимов, когда состояние движущейся частицы не зависит от времени U = const, оно имеет вид:
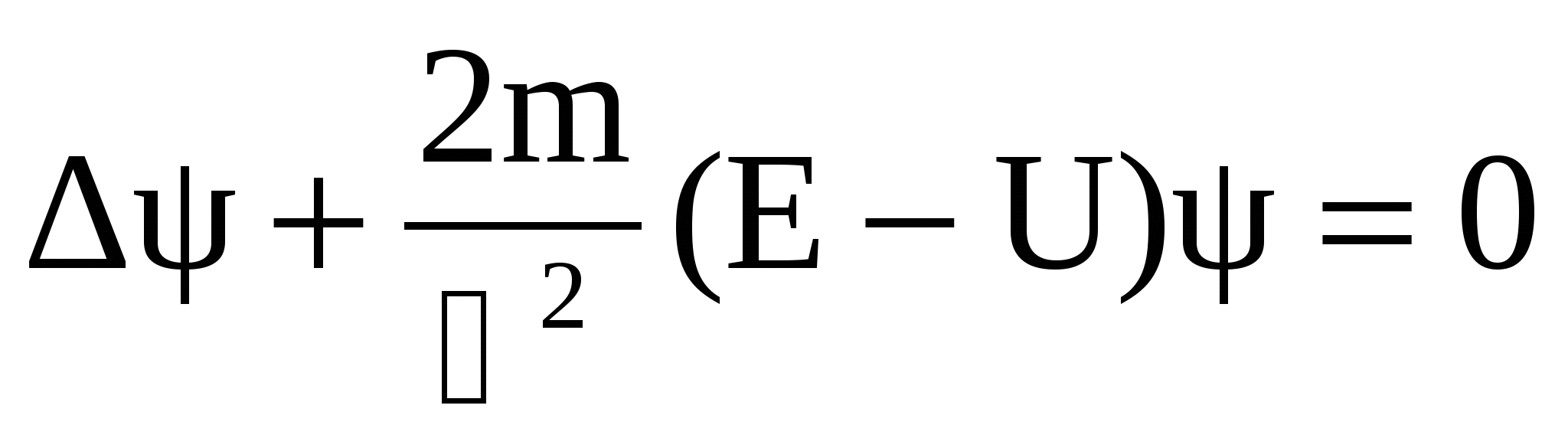 , (13) , (13)
где 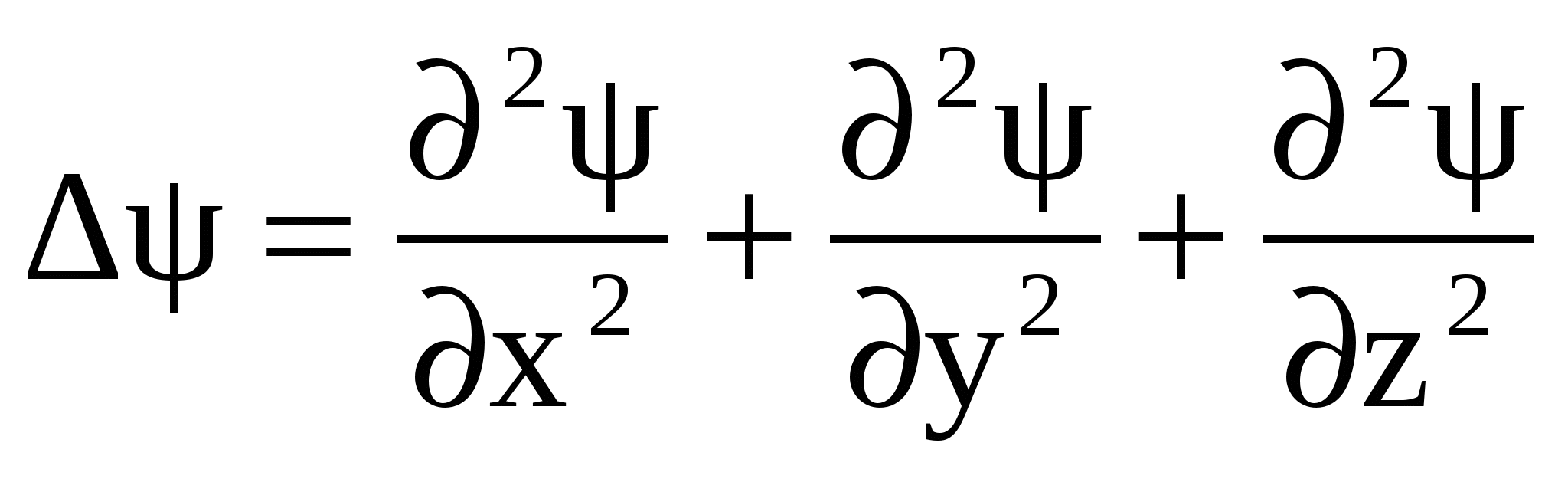 - оператор Лапласа, m – масса частицы, Е и U – полная и потенциальная энергии частицы. - оператор Лапласа, m – масса частицы, Е и U – полная и потенциальная энергии частицы.
Следует иметь в виду, что уравнение Шредингера нельзя вывести из каких-либо ранее известных соотношений. Оно постулируется на основе большого числа опытных данных, подобно тому, как это имело место с законами динамики Ньютона. Правильность этого уравнения подтверждается согласием с опытом результатов, которые получают с его помощью. Это, в свою очередь, придает ему характер закона природы.
ЭЛЕКТРОН В ПОТЕНЦИАЛЬНОЙ ЯМЕ
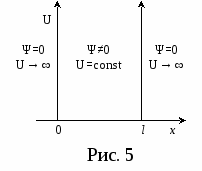
Рассмотрим, в качестве примера использования уравнения Шредингера, задачу о движении частицы вдоль оси х-ов в пределах 0 ‹ х ‹ l. Это означает, что ψ = 0, а U→ ∞ – при х ≤ 0 и при х ≥ l. Внутри заданного интервала, при 0 ‹ х ‹ l – ψ ≠ 0, а U = const. Выберем нулевой уровень потенциальной энергии так, чтобы он совпадал с осью х-ов. Тогда внутри интервала U = 0, а Е (полная энергии) в уравнении Шредингера (13) – это только кинетическая энергия частицы. Теперь (13) примет вид:
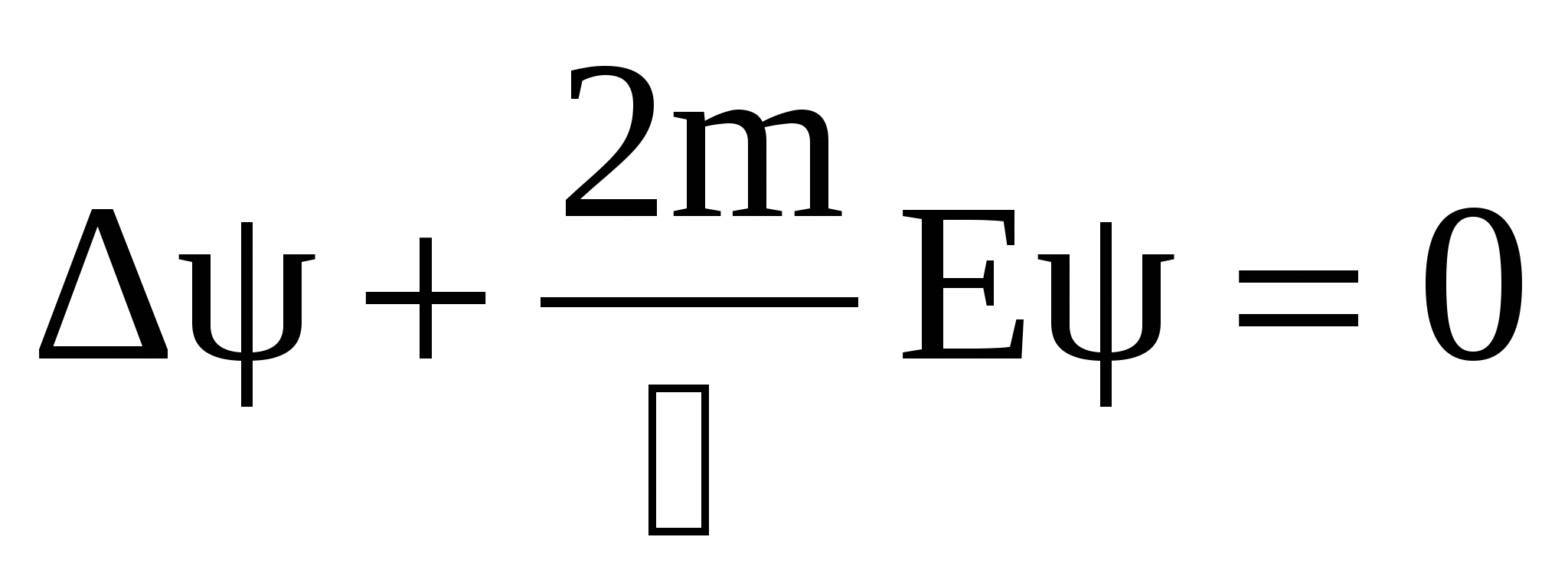 . (14) . (14)
Обозначим: 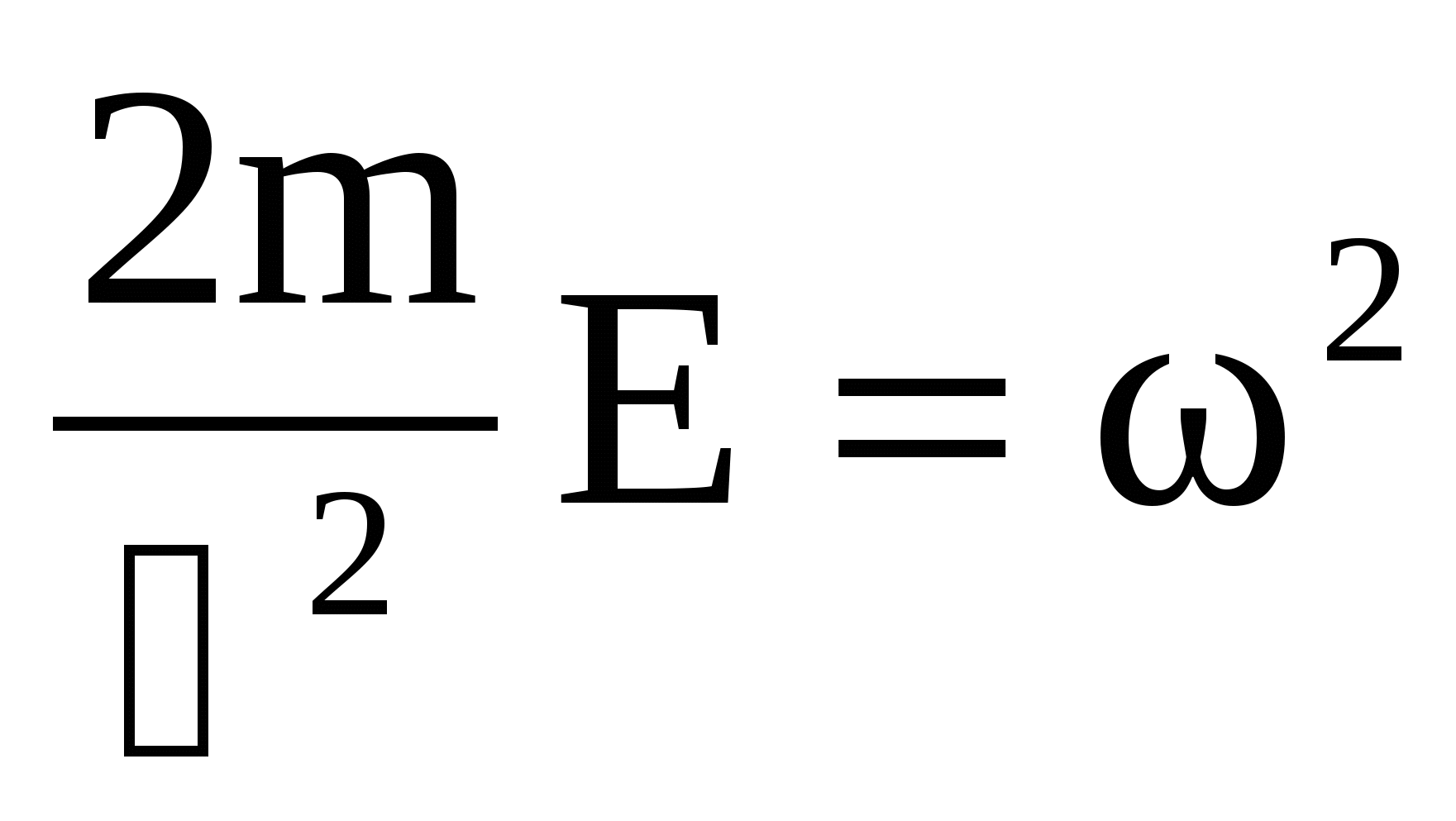 (15) (15)
С учетом (15), (14) перепишется:
Δψ + ω2ψ = 0. (16)
Это однородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Его решение имеет вид (см. Лк. №3):
Ψ(х) = А sin (ωх + α0 ). (17)
Используя граничные условия, найдем для х = 0: Ψ(0)=Аsinα0 = 0, выполняется при α0 = 0. С учетом этого факта для х = l: Ψ(l) =А sinωl = 0. Это возможно, если ωl = ± πn, где n =1,2,3…Следовательно, 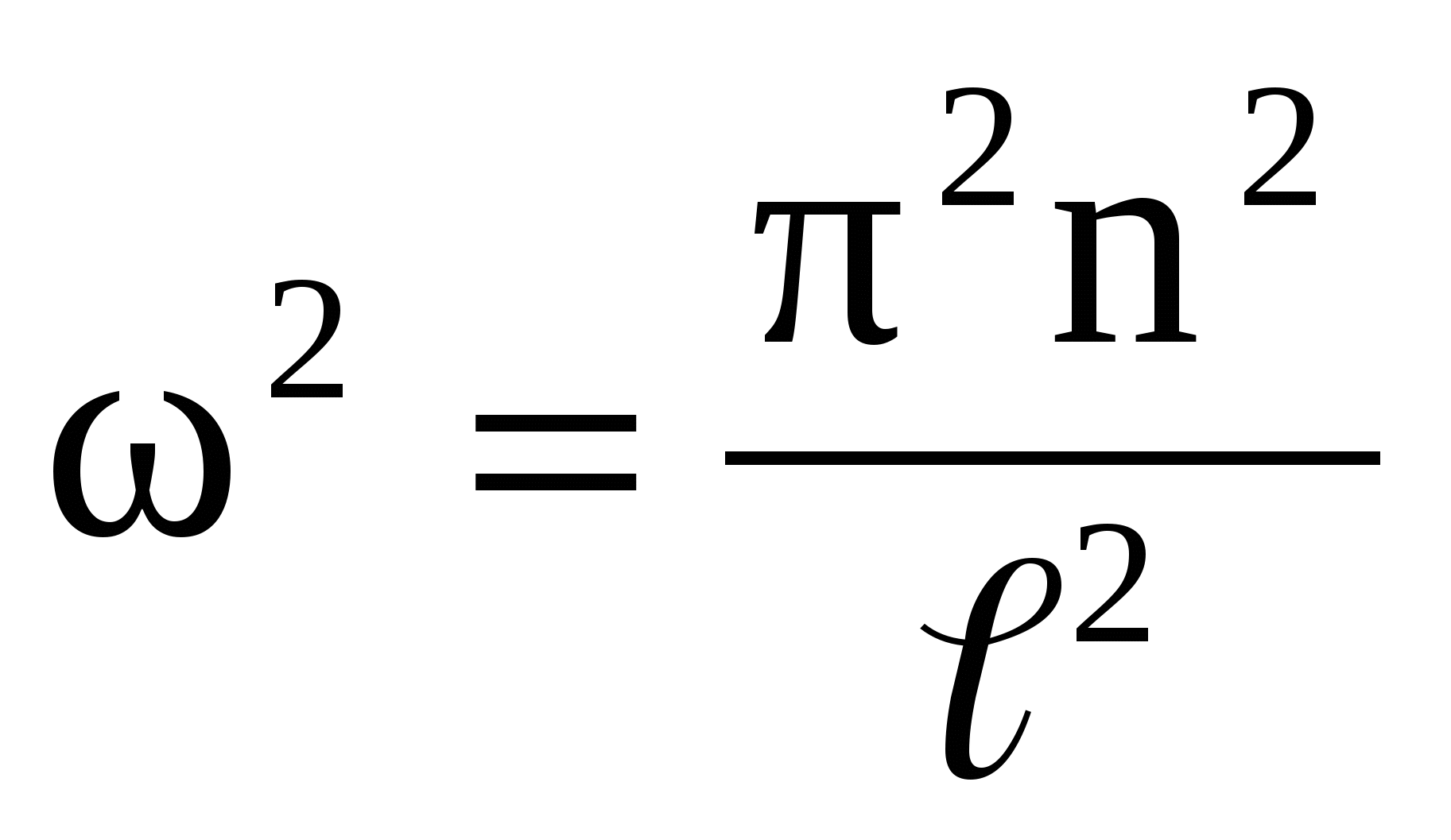 и из соотношения (15), для Е, получим: и из соотношения (15), для Е, получим:
 . (18) . (18)
Т.о., микрочастица в потенциальной яме может иметь только определенные значения энергии, т.е. энергия квантуется.
Оценим расстояние между соседними уровнями:
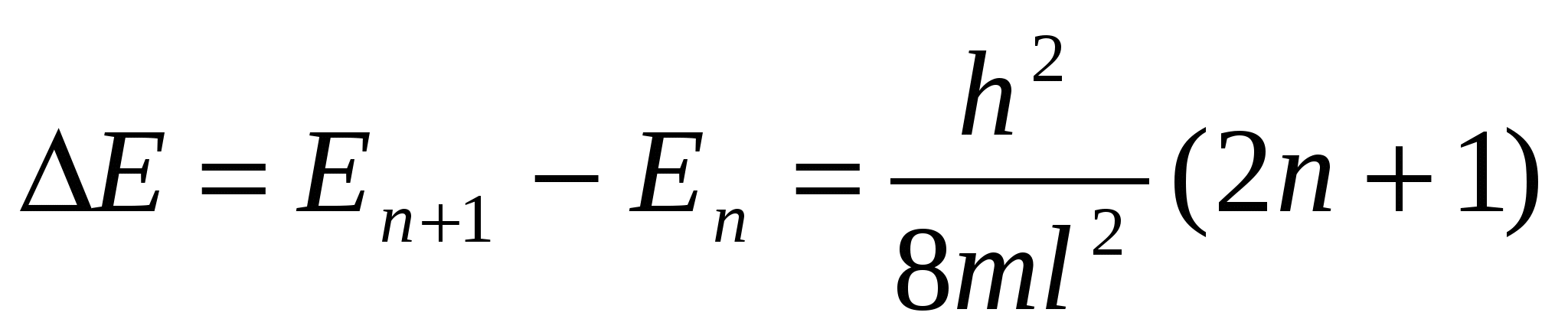 . (19) . (19)
При m 10-31 кг, n =1 и l 10-10 м – ∆Е 4,5 эВ, что хорошо согласуется с данными по водороду. Если l 10-1 м, когда электрон можно считать свободным, то ∆Е 10-16 эВ, т.е. энергетические уровни практически сольются.
Определим амплитуду А волновой функции. Воспользуемся для этого условием нормировки:
 . .
Проинтегрировав, получим 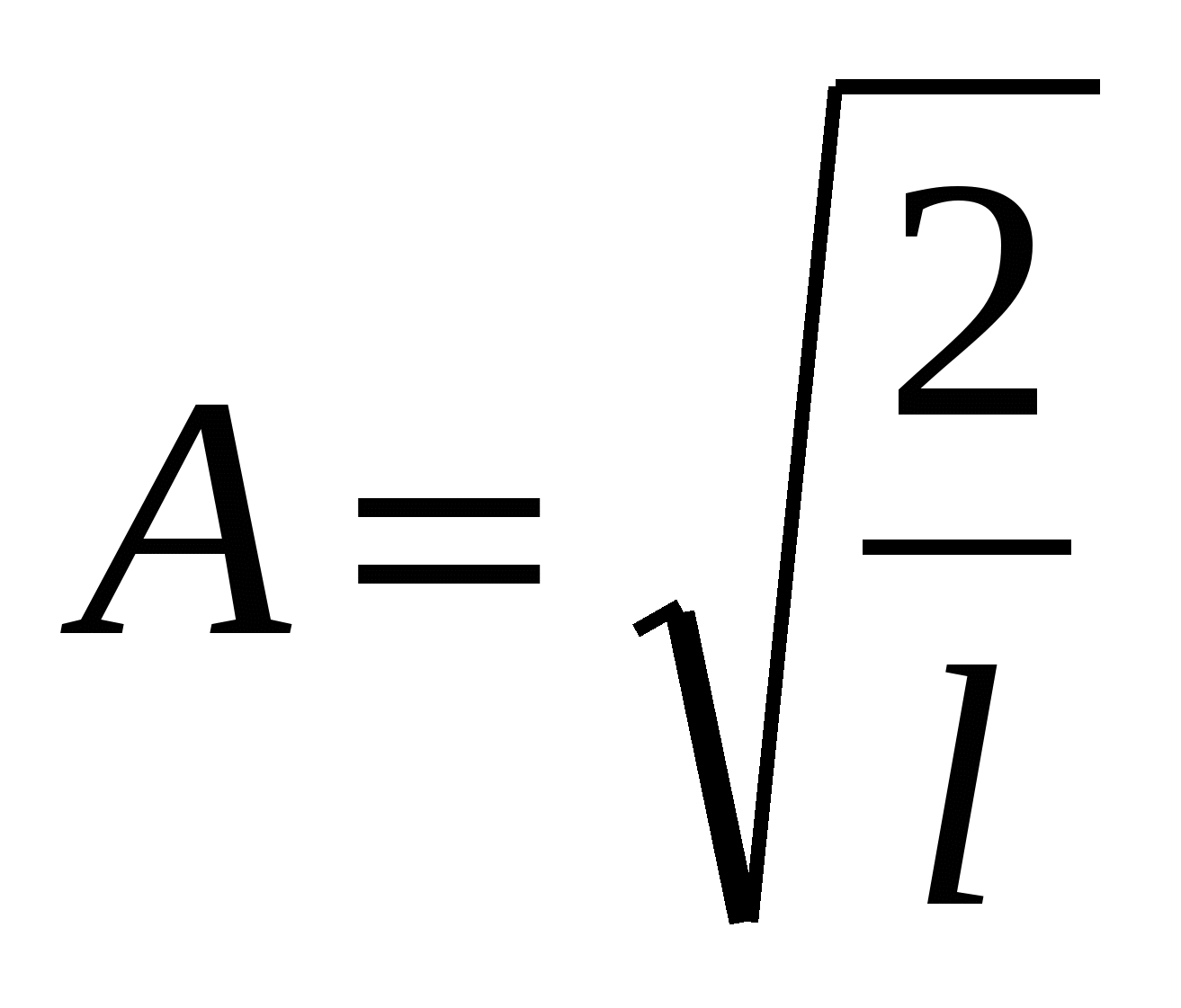 . Подставив в (17) ω = πn / l и выражение для амплитуды А, получим окончательный вид волновых функций: . Подставив в (17) ω = πn / l и выражение для амплитуды А, получим окончательный вид волновых функций:
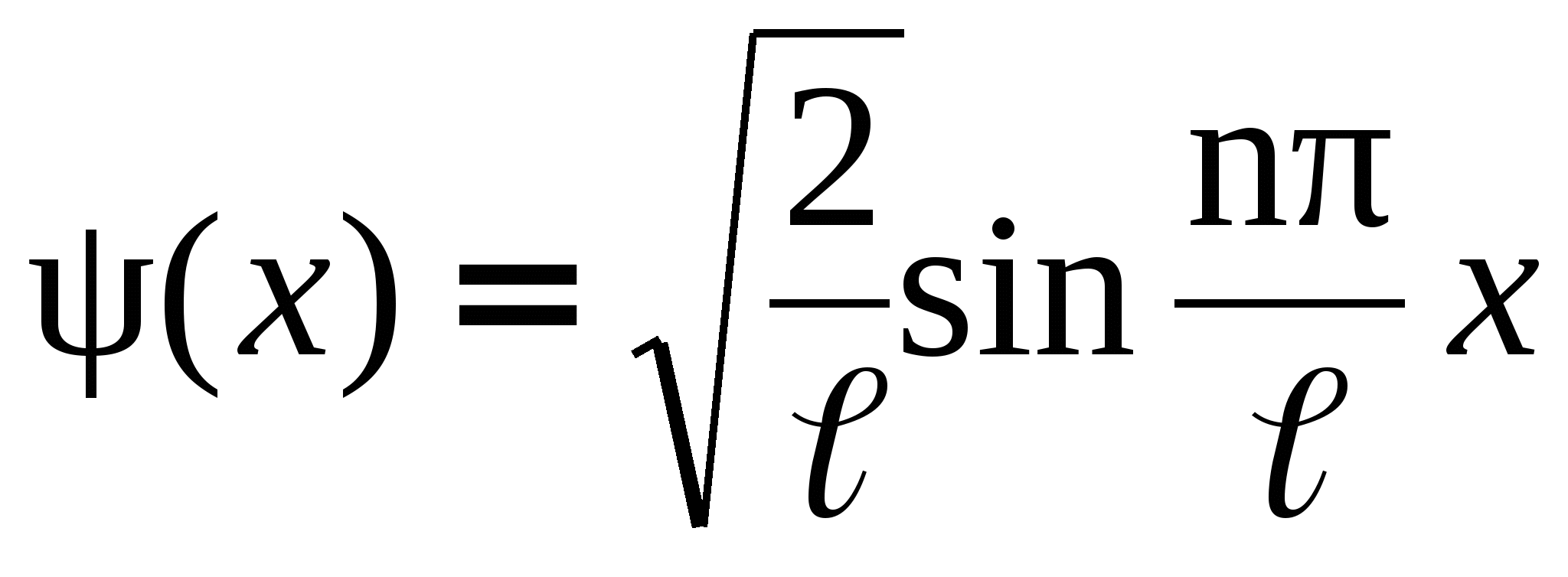 , (n = 1, 2, 3…) (20) , (n = 1, 2, 3…) (20)
 (21) (21)
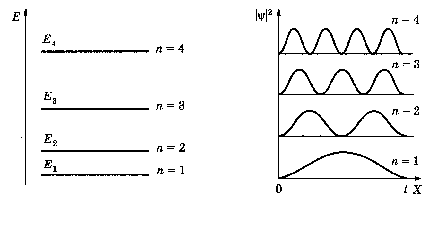
На рис.5а схематически показаны энергетические уровни Е1, Е2, Е3 и Е4, соответствующие разным квантовым состояниям электрона в потенциальной яме. На рис.5б приведены графики зависимости ψ 2 от х для n = 1, 2, 3 и 4. Как видно из графиков, вероятность нахождения электрона в разных местах потенциальной ямы, по представлениям квантовой механики, не одинакова. Есть такие точки, в которых вероятность нахождения электрона равна нулю, что противоречит представлениям классической механики.
АТОМ ВОДОРОДА
Квантовомеханическое описание состояний атомов и молекул с помощью уравнения Шредингера является достаточно сложной задачей. Наиболее просто она решается для водородоподобных атомов, электронная оболочка которых содержит только один электрон: водород, однократно ионизированный гелий, двукратно ионизированный литий и т. д.
 Атом водорода состоит из одного протона и одного электрона. Т.к. масса протона многократно больше массы электрона, то можно считать, что электрон находится в электрическом потенциальном поле ядра и его потенциальная энергия Атом водорода состоит из одного протона и одного электрона. Т.к. масса протона многократно больше массы электрона, то можно считать, что электрон находится в электрическом потенциальном поле ядра и его потенциальная энергия
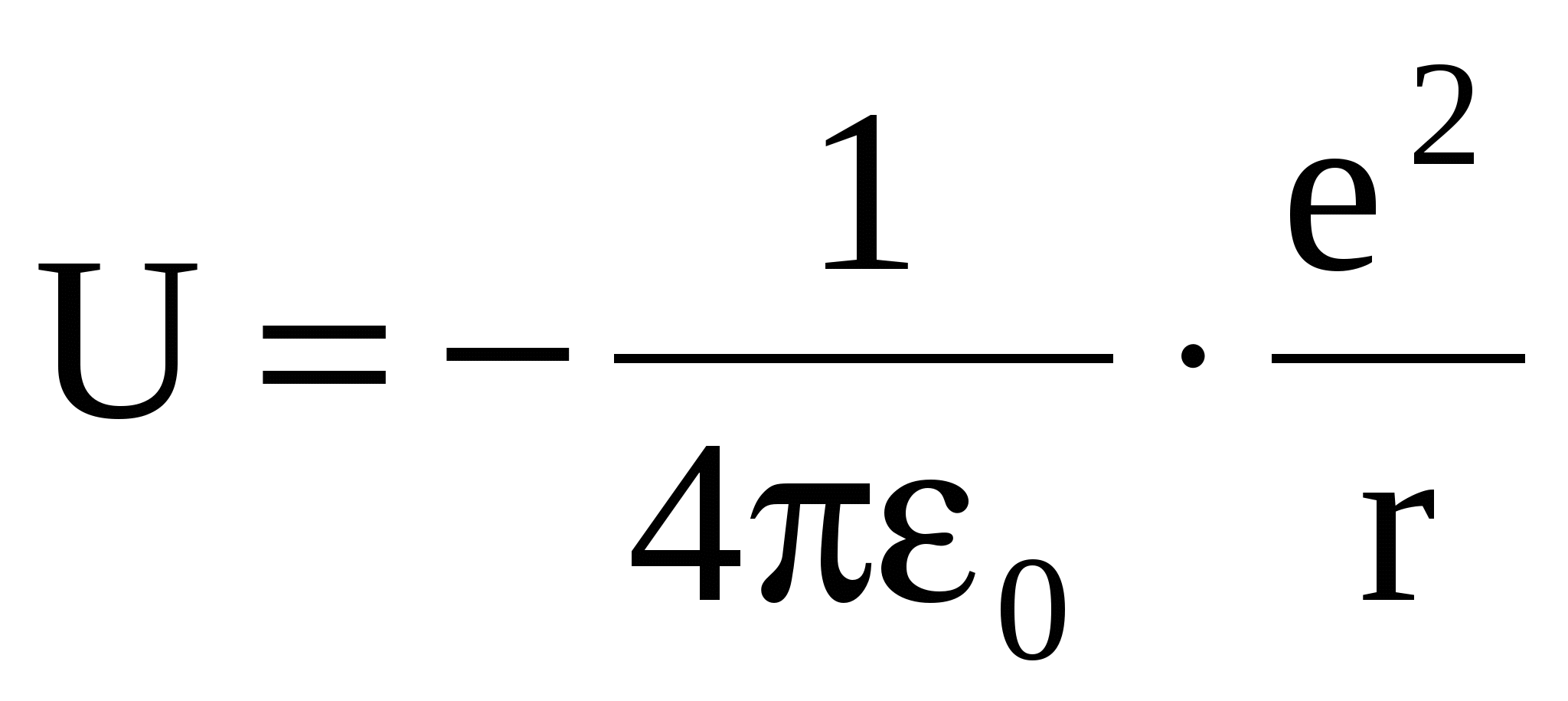 (22) (22)
Графически U = f(r) имеет вид потенци-альной ямы с гиперболическими стенка-ми и без дна. Уравнение Шредингера (13) примет вид:
 (23) (23)
Решение этого уравнения выходит за рамки наших возможностей. По этой причине ограничимся описанием результатов этого решения.
Отметим, прежде всего, что т.к. это пространственная задача, то решение можно представить в виде трех функций, каждая из которых зависит только от одной переменной – х, y или z. Каждая из них представляет собой дискретный набор решений вида (20), за который отвечает определенный набор целых чисел, которые называются квантовыми. Здесь проявляется главная особенность квантово-механических систем – дискретность физических величин, определяющих их состояние.Во-вторых,функции, удовлетворяющие требованиям однозначности, конечности и непрерывности, и, являющиеся решениями уравнения (23), существуют только в том случае, если собственные значения энергии электрона в атоме равны:
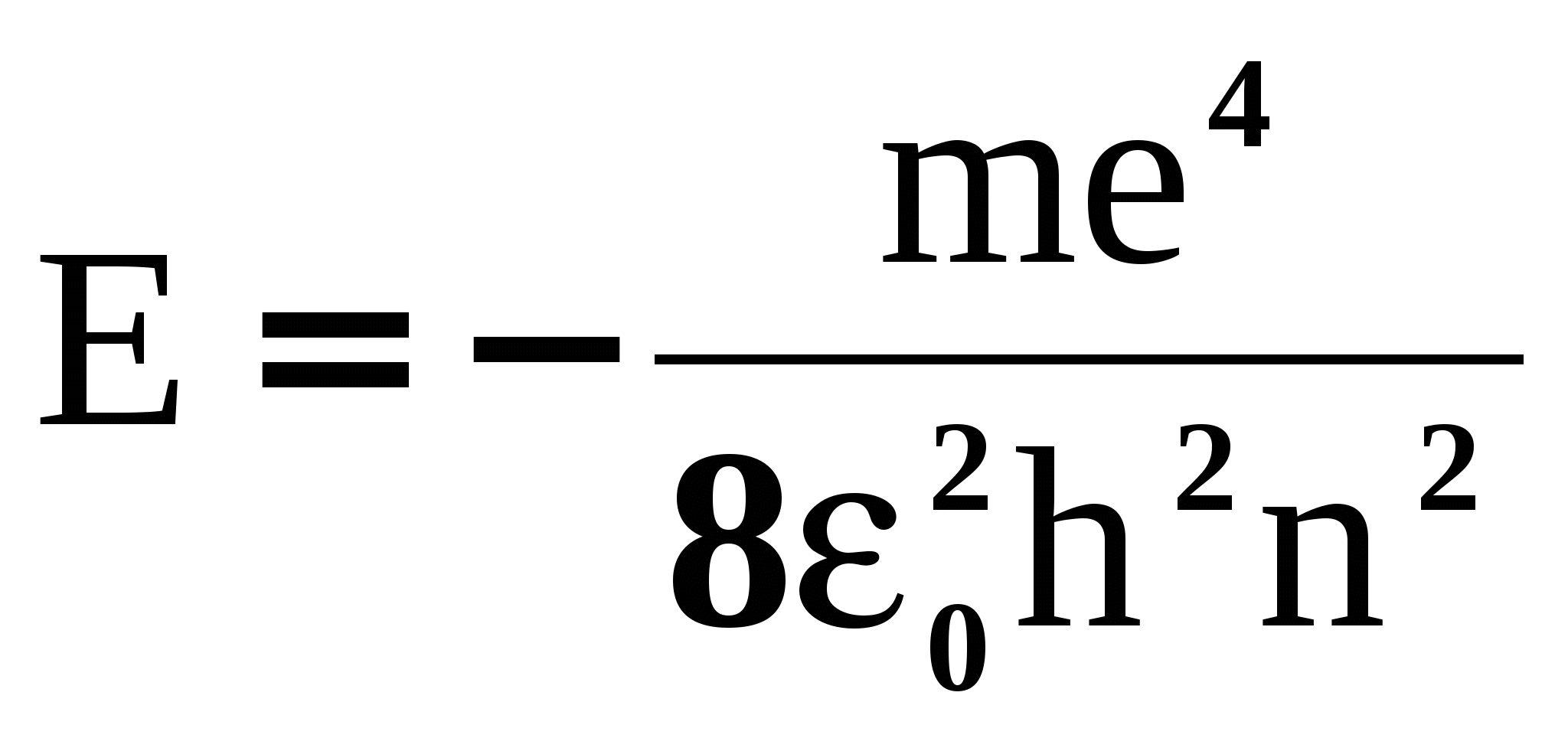 , (24) , (24)
где n – главное квантовое число (n = 1, 2, 3, 4…), которое определяет уровни полной энергии электрона.
Из решения уравнения Шредингера вытекает также, что орбитальный момент импульса электрона тоже квантуется.
Орбитальное (азимутальное) квантовое число l (или ml) определяет дискретные значения орбитального момента импульса электрона относительно ядра.
 . (25) . (25)
При заданном n, l принимает значения: 0, 1, 2, … n-1.
Магнитное квантовое число – ml определяет значения проекций момента импульса Le на любое выбранное направление Z.
Le,z=mlħ . (26)
При заданном l, ml принимает значения: 0, ±1, ±2, ±3…±l. В соответствии с этим 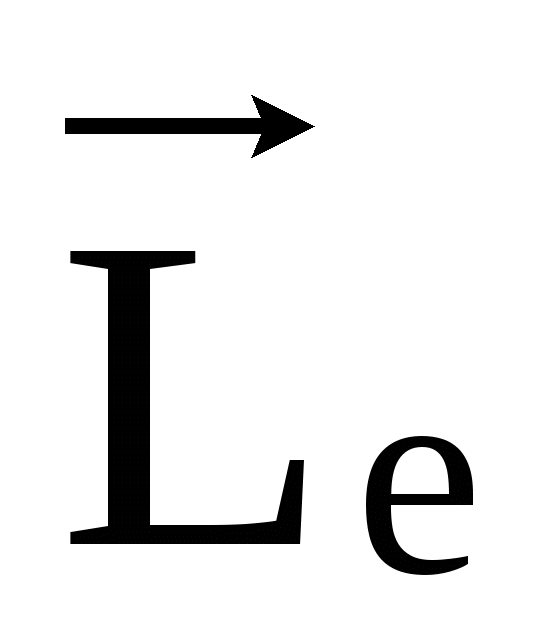 может иметь только такие ориентации в пространстве, для которых выполняется (26), т.е. Le может иметь 2l+1 ориентацию в атоме. может иметь только такие ориентации в пространстве, для которых выполняется (26), т.е. Le может иметь 2l+1 ориентацию в атоме.
Таким образом каждому En (кроме Е1) будет соответствовать несколько волновых функций ψn,l,mс разными l и ml. Это означает – атом водорода может иметь одно и то же значение энергии, находясь в нескольких различных состояниях – всего их n2.
В 1822 г. было обнаружено, что электрон обладает собственным неуничтожимым механическим моментом импульса, который не связан с орбитальным движением. Этот собственный момент назвали спином. Спин электрона и всех других микрочастиц квантуется.
Спиновое квантовое число s (или ms) собственный моментом импульса электрона:
 . (27) . (27)
По аналогии с орбитальным моментом проекция спина квантуется так, что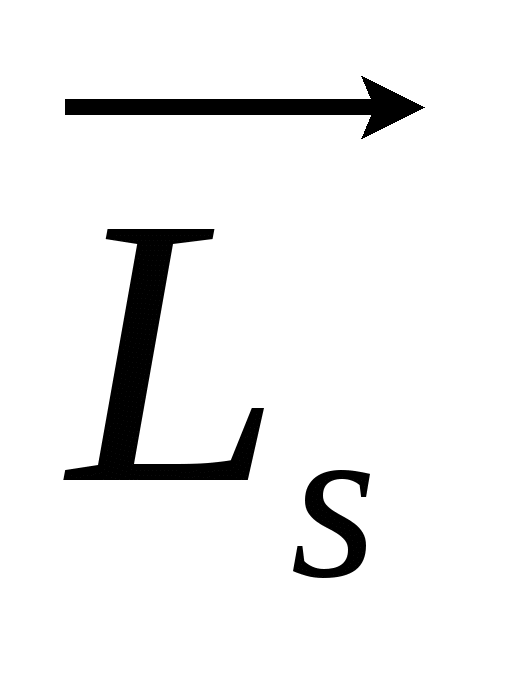 может принимать 2s+1 положение в атоме. Впоследствии выяснили, что может принимать 2s+1 положение в атоме. Впоследствии выяснили, что 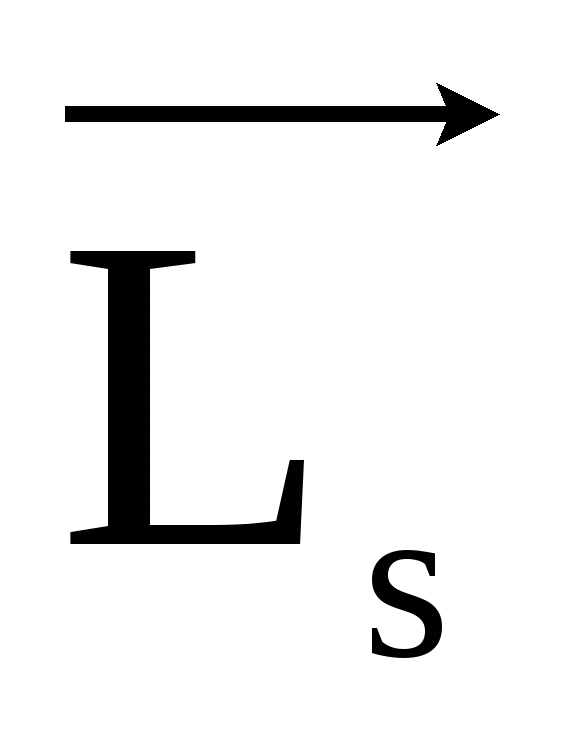 в атоме может иметь только два положения, т.е. 2s+1 = 2, тогда s, определяющее возможные значения проекции спина на направление Z будет – s = + ½ , а величина проекции в атоме может иметь только два положения, т.е. 2s+1 = 2, тогда s, определяющее возможные значения проекции спина на направление Z будет – s = + ½ , а величина проекции
Ls,z= ħs (28)
Т.о. всего оказалось четыре квантовых числа, что увеличивает число состояний электрона с одним и тем же значением En до 2n2.
С равнение показывает, что квантовая механика приводит к тем же результатам и выводам, что и теория Бора. Но в теории Бора эти результаты просто постулировались. В квантовой механике они получены логическим путем из уравнения Шредингера . равнение показывает, что квантовая механика приводит к тем же результатам и выводам, что и теория Бора. Но в теории Бора эти результаты просто постулировались. В квантовой механике они получены логическим путем из уравнения Шредингера .
Согласно квантовой механике, каждому энергетическому состоянию соответствуют волновые функции, квадрат модуля которых определяет вероятность нахождения электрона в объеме ∆V, а произведение е|ψ|2 среднее значение плотности заряда в этом элементе объема. Т. к. вероятность обнаружения электрона в различных частях атома разная, то и электронная плотность распределяется вокруг ядра атома неравномерно, т. е. электрон как бы размазывается по всему объему атома, образуя электронное облако. Причем, размер и форма электронного облака определяется квантовыми числами n и l, а его ориентацию в пространстве характеризует квантовое число – ml. На рис. 6 представлена фотомодель электронного облака. Из рисунка видно, насколько условно понятие «орбита» применительно к движению электрона в атоме.

ПРАВИЛА ЗАПОЛНЕНИЯ ЭНЕРГЕТИЧЕСКИХ УРОВНЕЙ
Распределение электронов по уровням происходит по общему правилу: электроны невозбужденного атома занимают состояния с наименьшей энергией и в соответствии с принципом Паули, который гласит: в атоме не может быть даже двух электронов с одинаковым набором квантовых чисел.
Совокупность электронов с одним и тем же n образуют слой. В каждом слое электроны с данным значением l образуют оболочку. (Примечание: иногда в литературе слой называют «оболочкой», в этом случае электроны с одним l образуют «подоболочку»).
главное квант. число - n
|
1
|
2
|
3
|
4
|
5
|
символ слоя
|
K
|
L
|
M
|
N
|
O
|
макс. число электронов в слое
|
2
|
8
|
18
|
32
|
50
|
орбитальное квант. число – l
|
0
|
0
|
1
|
0
|
1
|
2
|
0
|
1
|
2
|
3
|
|
символ
оболочки
|
1s
|
2s
|
2p
|
3s
|
3p
|
3d
|
4s
|
4p
|
4d
|
4f
|
|
макс. число электронов в оболочке
|
2
|
2
|
6
|
2
|
6
|
10
|
2
|
6
|
10
|
14
|
|
Заполнение по этому признаку идет до 18Ar (аргон). У следующих за ним атомов 19К и 20Са, заполняются оболочки 4s. Это связанно с тем, что из-за более сильного экранирования электронов оболочки 3d, оболочка 4s характеризуется более низкой энергией.
В целом заполнение слоев происходит по правилам Клечковского:
От оболочек с меньшим значением суммы квантовых чисел (n+l) к оболочкам с большей суммой (n+l).
  Пример: 18Ar 3p (3+1) = 4 Пример: 18Ar 3p (3+1) = 4
  19К 3d (3+2) = 5 19К 3d (3+2) = 5
  19К 4s (4+0) = 4 – реализуется. 19К 4s (4+0) = 4 – реализуется.
  20Са 4s (4+0) = 4, s – оболочка заполнена. 20Са 4s (4+0) = 4, s – оболочка заполнена.
  21Sc 3d (3+2) = 5 21Sc 3d (3+2) = 5
 4p ( 4+1) = 5 Какая из них реализуется? 4p ( 4+1) = 5 Какая из них реализуется?
При одинаковом значении (n+l) – от оболочек с меньшим n к оболочкам с большим n.
Это значит в 21Sc (Sc - скандий) будет заполняться 3d оболочка.
У этих правил, есть исключения, например, лантан – 57La , церий – 58Cc и элементы 7–ой группы таблицы Менделеева.
Анализ хода заполнения оболочек у разных химических элементов показывает:
Общее число электронов в атоме химического элемента, а следовательно и заряд ядра, равно порядковому номеру элемента в периодической таблице Менделеева.
Число электронных слоев равно номеру периода, к которому относится элемент.
Число электронов во внешнем слое равно номеру группы, занимаемой элементом в этой таблице.
|
 Скачать 397 Kb.
Скачать 397 Kb. ткрытие волновых свойств микрочастиц привело к появлению новых исследовательских физических методов. Аналогично рентгеноструктурному анализу дифракцию частиц можно использовать для оценки степени упорядоченности в расположении атомов и молекул в веществе, также для измерения параметров кристаллической решётки. В настоящее время широкое распространение имеют электронография (основана на дифракции электронов) и нейтронография (дифракция нейтронов).
ткрытие волновых свойств микрочастиц привело к появлению новых исследовательских физических методов. Аналогично рентгеноструктурному анализу дифракцию частиц можно использовать для оценки степени упорядоченности в расположении атомов и молекул в веществе, также для измерения параметров кристаллической решётки. В настоящее время широкое распространение имеют электронография (основана на дифракции электронов) и нейтронография (дифракция нейтронов).

 Пример: 18Ar 3p (3+1) = 4
Пример: 18Ar 3p (3+1) = 4
 19К 3d (3+2) = 5
19К 3d (3+2) = 5
 19К 4s (4+0) = 4 – реализуется.
19К 4s (4+0) = 4 – реализуется.
 20Са 4s (4+0) = 4, s – оболочка заполнена.
20Са 4s (4+0) = 4, s – оболочка заполнена.
 21Sc 3d (3+2) = 5
21Sc 3d (3+2) = 5  4p ( 4+1) = 5 Какая из них реализуется?
4p ( 4+1) = 5 Какая из них реализуется?
 о прохождения через щель pх = 0; ∆pх = 0, а координата x не определена, т.е. ∆x→ ∞. В момент прохождения через щель координата электрона имеет неопределенность ∆x равную ширине щели. В то же время, из-за дифракции, электроны отклоняются от первоначального направления и будут двигаться в пределах угла 2φ, где φ – угол дифракции. Теперь появляется неопределенность в значении составляющей импульса вдоль оси x-ов:
о прохождения через щель pх = 0; ∆pх = 0, а координата x не определена, т.е. ∆x→ ∞. В момент прохождения через щель координата электрона имеет неопределенность ∆x равную ширине щели. В то же время, из-за дифракции, электроны отклоняются от первоначального направления и будут двигаться в пределах угла 2φ, где φ – угол дифракции. Теперь появляется неопределенность в значении составляющей импульса вдоль оси x-ов: 

 Атом водорода состоит из одного протона и одного электрона. Т.к. масса протона многократно больше массы электрона, то можно считать, что электрон находится в электрическом потенциальном поле ядра и его потенциальная энергия
Атом водорода состоит из одного протона и одного электрона. Т.к. масса протона многократно больше массы электрона, то можно считать, что электрон находится в электрическом потенциальном поле ядра и его потенциальная энергия равнение показывает, что квантовая механика приводит к тем же результатам и выводам, что и теория Бора. Но в теории Бора эти результаты просто постулировались. В квантовой механике они получены логическим путем из уравнения Шредингера .
равнение показывает, что квантовая механика приводит к тем же результатам и выводам, что и теория Бора. Но в теории Бора эти результаты просто постулировались. В квантовой механике они получены логическим путем из уравнения Шредингера . 