физика. лекция 1. Лекция 1 Электростатика
 Скачать 1.03 Mb. Скачать 1.03 Mb.
|
|
Курс электричества Физика Лекция 1 Электростатика Электростатика изучает взаимодействие неподвижных точечных электрических зарядов и свойства агента, передающего это взаимодействие ,т.е свойства электрического поля, при условии, что это поле постоянное Электростатика – раздел учения об электричестве, изучающий взаимодействие неподвижных электрических зарядов и свойства постоянного электрического поля 1. Электрический заряд. Единица электрического заряда – кулон (Кл) – электрический заряд, проходящий через поперечное сечение проводника при силе тока 1 ампер за время 1 секунда. Основные понятия: Основным понятием электростатики является понятие точечного заряда. Точечный заряд - это модель, описывающая те объекты, которые мы будем рассматривать. Точечный заряд -заряженная материальная точка , т.е такой объект, размерами которого можно пренебречь в условиях данной задачи ,и который несет на себе электрический заряд Экспериментально было выяснено, что в природе существуют два рода зарядов «+» и «–» Их назвали, потому что удобно для математического описания Могли и бел/черн, вкусн/против Два рода знаков, которым приписали знаки Причем заряды одного вида отталкиваются, а заряды противоположного знака притягиваются Элементарный заряд , самый маленький из всех возможных принадлежит электрону Электрон- это отрицательная заряженная частица, его заряд равен 1,6⋅10–19 Кл. Существует элементарный (минимальный) электрический заряд e =-1,6⋅10–19 Кл. Носитель элементарного отрицательного заряда – электрон. Его масса me = 9,11⋅10–31 кг Меньше заряда в природе нет. Все остальные заряды складываются и элементарных зарядов. Носитель элементарного положительного заряда – протон. Его масса mp = 1,67⋅10–27 кг. Это элементарная частица, заряд, которого равен P=+1,6⋅10–19 Кл По модулю равны, но противоположны по знаку Массы этих частиц очень различны Масса электрона по порядку величины составляет me = 9,11⋅10–31 кг, то протон имеет массу mp = 1,67⋅10–27 кг. Кроме частиц элементарных каждой частице соответствует античастица. Античастицы – частицы, соответствующие каждой частице, например, электрон –позитрон ,все одинаково с электроном(масса покоя и т.д), но заряд положительный. Частица эта нестабильная. Если она возникает и встречается с электроном, аннигилируют и перестают существовать как частицы, превращаются в два гамма-кванта энергии , т.е, в поле – реакция аннигиляция Итоги: Основная модель –точечный заряд Носитель отрицательного знака – электрон Носитель положительного знака-протон Протон тяжелее электрона. По модулю заряд одинаковый. По знаку же отличаются. Единица электрического заряда – кулон (Кл) – электрический заряд, проходящий через поперечное сечение проводника при силе тока 1 ампер за время 1 секунда Электрический заряд инвариантен относительно любых преобразований т.е его величина не зависит от выбора системы отсчета , от того движется этот заряд или покоится, нагревают проводник или охлаждают, т.е. от внешних условий электрический заряд не зависит его величина. Электрический заряд инвариантен – его величина не зависит от системы отсчета, т.е. от того, движется он или покоится Экспериментально было выяснено что электрический заряд аддитивен, т.е заряд любой системы частиц или тел входящих в эту систему равен сумме зарядов этих частиц или тел, которые входят в эту систему Электрический заряд аддитивен – заряд любой системы тел (частиц) равен сумме зарядов тел (частиц), входящих в систему. Одним из фундаментальных законов физики является закон сохранения заряда, а именно алгебраическая сумма электрических зарядов любой замкнутой системы остается неизменной, какие бы процессы не происходили внутри данной системы Электрический заряд подчиняется закону сохранения заряда: Алгебраическая сумма электрических зарядов любой замкнутой системы остается неизменной, какие бы процессы ни происходили внутри данной системы Под замкнутой системой в данном случае понимают систему, которая не обменивается зарядами с внешними телами. Замкнутая система- система, составляющие которой взаимодействуют между собой внутри этой системы и не взаимодействуют с никакими компонентами, не входящими в эту систему. Основным законом электростатики является закон Кулона. 1)Для вакуума: если два неподвижных точечных заряда находятся в вакууме, то они взаимодействуют между собой силой, прямо пропорциональной величинам этих зарядов и обратно пропорциональной квадрату расстояния между ними. Сила эта действует вдоль прямой, соединяющей эти заряды, и направлена вдоль прямой таким образом, что если заряды одноименные, то эти силы направлены в противоположную сторону, а если разноименные, то они притягиваются друг другу, т.е силы тоже направлены противоположно другу другу. Закон кулона: два точечных неподвижных заряда в вакууме взаимодействуют между собой с силой, величина которой прямо пропорциональна величинам взаимодействующих зарядов, обратно пропорциональна квадрату расстояния между ними и действующими вдоль прямой, соединяющей эти заряды, причем одноименные заряды отталкиваются, разноименные притягиваются друг другу В формуле для выражения закона Кулона важно наличие модулей у зарядов , т.к заряды разными бывают. Коэффициент пропорциональности в СИ (1)  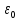 -электрическая постоянная- это фундаментальная константа, которая -электрическая постоянная- это фундаментальная константа, которая 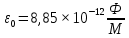 (Фарад на метр) (Фарад на метр)Если электрическую постоянную 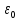 и численное значение подставить в коэффициент пропорциональности и посчитать , то получается и численное значение подставить в коэффициент пропорциональности и посчитать , то получается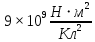 Взаимодействие может происходить и в других средах : вода, диэлектрик Выяснили опытным путем, что в любой среде сила взаимодействия двух точеных неподвижных зарядов отличается от силы взаимодействия тех же зарядов, находящихся таком же расстоянии, только в вакууме. Отношение силы взаимодействия двух неподвижных точечных зарядов в вакууме, находящихся на расстоянии r друг от друга в вакууме к силе взаимодействия этих же зарядов, находящихся на этом же расстоянии друг от друга некоторой среде, называется диэлектрической проницаемостью среды. (всегда больше 1) 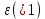 - диэлектрическая проницаемость среды - диэлектрическая проницаемость средыЕсли учесть этот факт, то в любой среде закон кулона будет выглядеть как на 4 слайде, т.е сила взаимодействия будет пропорциональна величинам этих заряда и обратно пропорциональна квадрату расстояния между ними, но коэффициент пропорциональности другим будет (формула снизу)  Так как силу взаимодействия сравнивают с силой взаимодействия в вакууме , получается, что сила взаимодействия двух зарядов, находящихся на определенном расстоянии друг от друга, является максимальной по отношению к любой другой среде. Диэлектрическая проницаемость вакуума = 1 Диэлектрическая проницаемость сухого воздуха 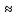 1 1Для всех остальных веществ 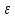 >1 >1У воды 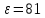 , вода ослабляет силу взаимодействия зарядов в 81 раз. Керосин , вода ослабляет силу взаимодействия зарядов в 81 раз. Керосин 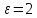 , стекло , стекло 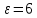 , парафин , парафин 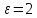 , масло , масло 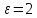 Закон Кулона можно записать в векторной форме Сила взаимодействия- это вектор Для этого нужно определить направление действии силы Если рассматриваем силу, действующую на один из зарядов, то для этого заряда можем провести радиус-вектор, он будет иметь направление, длина равна расстоянию между зарядами. В таком случае достаточно радиус-вектор разделить на его модуль, и мы получим направление действия силы.  Закон Кулона как и все фундаментальные законы получен результатом обобщения большого числа экспериментов. Эксперимент, который привел к пониманию формы взаимодействия зарядов, был сделан с помощью крутильных весов- это маленькое коромысло, подвешенное на упругой тонкой невесомой нити , нерастяжимой нити, по углу закручивания которого можно судить о том, какое взаимодействие получает , какую силу получает то или иное взаимодействие. Такие весы были использованы для гравитационной постоянной Кавендиш. Формула Кулона напоминает закон всемирного тяготения. Закон всемирного тяготения выражает гравитационное взаимодействия, а закон Кулона - электромагнитное Должен существовать такой единый закон, который описывал бы все типы взаимодействия. Вид этого закона Эйнштейн искал, когда теорию относительности выводил. Как взаимодействуют заряды? Можно обнаружить заряд еще одним зарядом По силе взаимодействия между ними можно узнать, что в пространстве существует заряд По поведению пробного заряда можно судить, есть ли в пространстве еще заряды и какого они знака. Как они чувствуют? Это взаимодействие осуществляется посредством некоторого агента – электрического поля Про электростатическое поле будем говорить –поле неподвижного заряда. Любой заряд всегда окружен электростатическим полем. Существуют телевизоры –приборы, которые визуализируют тепловые излучения Все теплокровные существа излучают тепло, поэтому видны через прибор ночного видения. Они видят это тепловое излучение. Источник электрического поля – это электрический заряд Электрические заряды взаимодействуют посредством электрических полей, которые они сами создают в пространстве. Для того, чтобы оперировать этим понятием, ввели понятие напряженности электрического поля. Напряженность поля – это силовая характеристика электрического поля. Пробный заряд – единичный положительный заряд, который будем помещать в какую-то точку поля. Если величина этого заряда равна 1,то сила взаимодействия характеризует не столько оба этих взаимодействующих заряда, сколько пространства, в котором находится этот единичный заряд. Как возникла эта характеристика? У нас есть заряд в пространстве, зафиксированный с величиной и положением. На расстоянии r от этого заряда выберем точку, и в эту точку по очереди будем приносить разные заряды, которые будут разными по величине. Каждый раз будем измерять силы взаимодействия между нашим первым зарядом и теми зарядами, которые будем приносить в исследуемую точку. Каждый раз мы будем получать будем разные результаты, т.к разные заряды будем приносить. Если возьмем отношение силы взаимодействия с первым зарядом к величине этого пробного заряда, то будем получать одну и ту же величину – это и есть напряженность электростатического поля. Напряженность электростатического поля в некоторой точке равна силе действующей на единичный положительный заряд, помещенный в данную точку поля. 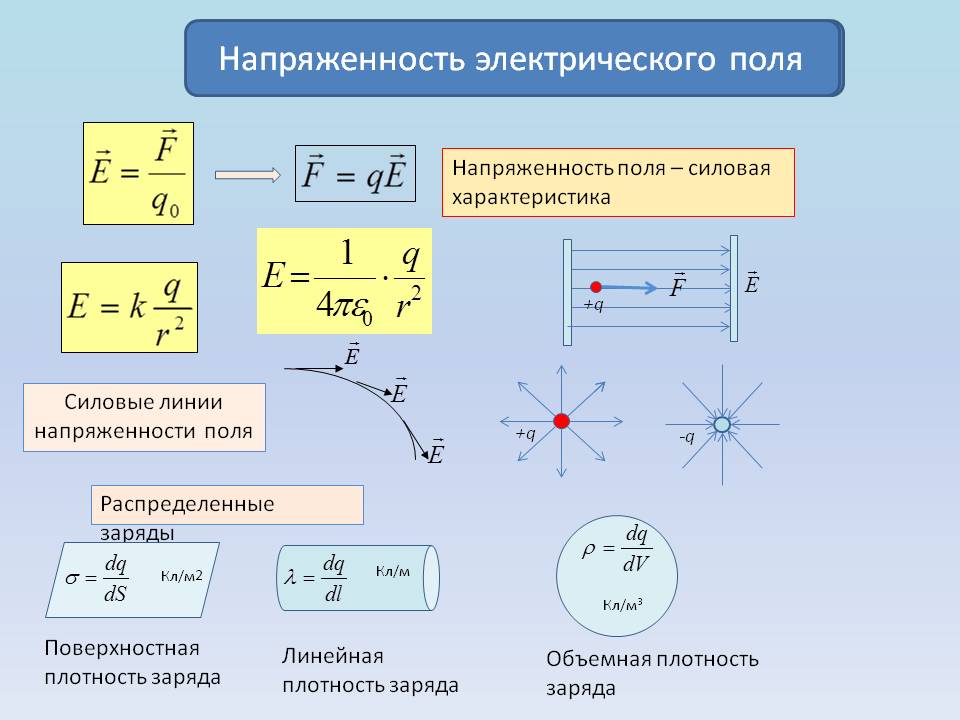 Линии напряженности электростатического заряда. Любой заряд окружен электростатическим полем, линии напряженности которого начинаются на положит зарядах и заканчиваются на отрицательных. В качестве пробного заряда удобно брать положительный заряд, т.к положительный заряд будет отталкиваться от положительного заряда создающего поля, и сила будет направлена по направлению линии поля, уходящего от положительного заряда. Если же заряд, который создает поле отрицательным, то линии напряженности направлены к нему, но положительный заряд будет притягиваться к нему, значит, сила, действующая на него, тоже будет направлена в сторону отрицательного заряда. Можем определить вектор напряженности поля как отношение силы взаимодействия двух зарядов, заряда, создающего поля, и пробного заряда, к величине этого пробного заряда.  Если сила F может быть рассчитана по Закону Кулона, то напряженность электростатического поля пропорциональна заряду, которая создает это поле и обратно пропорциональна квадрату расстояния от этого заряда до выбранной точки пространства. Как и в законе Кулона если эта ситуация развивается в вакууме, то коэффициент пропорциональности равен 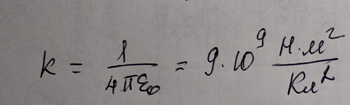 В любой среде: 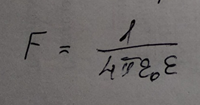 Зная электрическое поле (может однородным/неоднородным, однородное - напряженность поля во всех точках пространства одинаковая, неоднородным – в разных точках пространства напряженность поля может быть различной), напряженность поля в данной точке пространства характеризует эту точку полностью, т.е, если мы в эту точку пространства помещаем заряд и знаем напряженность поля в этой точке, то всегда знаем какая сила со стороны действует на этот заряд. Эта сила взаимодействия равна6  ,где ,где q- заряд данной точки поля, Е – ее напряженность. При этом неважно какой конкретно заряд создает это поле, так как поле может быть создано не одним зарядом, а целой системой зарядов, распределённым зарядом Заряды могут быть распределены в пространстве по- разному. Н-р, есть бесконечная длинная нить, на нее поместили эл.заряды равномерно, тогда можем говорить о линейной плотности заряда, т.е весь заряд можно разделить на длину этой нити. Если же не удалость равномерно распределить заряды, то можно выделить бесконечно малый участок этой нити, в пределах которого можно считать, что равномерность достигнута , и тогда линейная плотность заряда  Аналогично с поверхностной и объемной плотностями заряда. Заряд может быть, как размазан по поверхности или распределен по объему. Плозадь поверхности где он распеределен ,а чтобы найти объемный Может быть заряд распределн и по поверзности и в длину равномерно и это поле однороное Если напряженность различны то должны выбрать такой бесконечно малый обьем в пределах котрой можем считать однорожной тогжаповерхностн плосктсть Принцип суперпоизиции( независимости) эд.полей Предположим что в прост-ве есть несколько которые создаю Есть точка в которой хотели бы знать чему равно поле Эти два заряда внекоторй точке создабт кадлой свое собственное поле.положит создает напряденность Е1 , вектор которого красным обозначен, отриц заряд создает поле Е2, вектор голубой Т.к в этой тчоке есть два ветокра силовых, можем их векторно сложить , это черный вектор, который явялеся резульирубщим веткором Е1 и Е2, это выражае суперпоизицюб полей Если в прост-ве сущ система зарядов, каждый из которлых в неткорой точке созает свое собственное поле то резултирующие поля этой системы зарядов в выбраной тчок равно векторной сумме напряенностей полей создаваемых зарядами этой системы в выбранной точке т.к если бы остальных харядов не было. Т.е каждый заряд создаетс вое собстсвено поле и оно не зависит есть в жтой системе … Предсиавиь можно как цыт кожи Поток вектора напряженности Поток вектора через площадку какую-то – скалярное произведение двух векторов, этого вектора и вектора площадки ……… По положению этой нормали можно суить об ориентации этой плозадки Вектор площади будем определтяь как производенчи е велчиины площадки на навпрябщий вектор нормали к этой плозадки Обычно этот напрявющий вектор едичиный Вектор площади как величина площакди умн… Поток вектора через площадку какую-то – … Произвдеение модуля вектора напряженности поля на величину этой площакди9 модуль) на косинус угла между этими веткорами (вектор напряденности вектор нормали к этой площалке) Нормальной состаябщей на величину этой площадки Единциа измерения потока – В м Напраяженность – В/м Теорме астргарц гауса для расчет полей распределнных обхектов ….. У нас есть заряды в прос-ве, есть поврезность которые эти заряды внутрь себя включает Есть сфера с зарядами Заряд ку1 Тогда модем сказать поток векора напряденности элекростат.поля сквозь таую сферическую поверхность равен этому заряду окторый находится внутри этого поля деленного на эпсилон 0 Теорема. Поток вектора напряженности электростат.поля в вакууме через произвольную замкнутую поверхность равной алгебраической сумме зарядов заключенных внутри этой поверхности деленной на эл.постоянную-эпсилон 0. Поврезность может быть гладкой как сфера , может и быть складчатой как шукра щарпея Перерчение нечентное кол-во Четн кол-во будет давать другой знак Линия напряденности выходит из этой поверности, нормаль в внешней поверзности будет напрялена в ту же сторону чо и линии напряденности Когда выходит то нормаль в противполодную Внутри поверхноси нет зарядов тогда потомк равен 0, т к нет источника поля и …. Теорема Гаусса для электростатического поля в вакууме Поток ..равны инетгральному замнктуой поверхности S От вектора напряженности умноженного на веткор площадки ерез которую прпотом равен алгебраической сумме заряжов заключенных между деленной на жпсилон нулевое Нить на котрой с линейно плотностью Тао , пусть с линейной получился заряденная нитка. В прост-ве получает поле – неоднородное. Каждый заряд на этой нитке создает в прост-ве свое поле- радиалььное ( направлено во все стороны от этого заряда) Если посмотрим эти линии напряженности то похожит на ершик …… Напряженность поля щара заряженного по объему Шар с радиум Р распределен по обьему с обьемноц плотнотью зарядо ро вспомогате проведем поверхнось радиусом l тогжа потомк вектора напряженности поля по теорме гаусса будет равен тому заряду окторый находится внтури этой поверхности деленное на эпислон 0 поверзность определяется радиусом меньшим чем радиус щара т.е эта поверхность внутри шара поверхность ограничивает объем, считаем как объем шара если посчитаем этот же поток веткоры напряженности эл.поля через вспомогат поеврехность по поерделению то получим произведение e на 4/2… приравняв получем напряденность поля создаваемного обьемно заряженным щаром внутри этого шара если оказываемч в этой точке центре щара раиус повезнности равен 0 и напряженность поля 0, то внтури напряженность поля возрастаетл линейнно от 0 до величины пропорц r акой рост будет до тез пор пока r не станет R Если окажется на поверхности этого объемнозраяженного шара то напряженность поля становится равной напряженности полю точченчного заярда расположенного внутри, в центре этого заряженного щара . q получает равным обьем на объем всего шара Этот заряд распологается вцентре шара Если выходим за рамки этого шара Возьмем Чем радиус шара то получем поле точечного заряда коорый находится в центре заряденного щара Если построить график щависимость напояженности поля жто бущет неплавная кривая . Эта точка будет соотвествовать повехрност радиуса щара и что внутри щара будет линенйно возрастать от 0 до момента е сотвестующего радиуса жтого шара Вне напряженность поля будет уменьщатья обратно пропорциональном квадрата …до бесконечности, до БМВ Напряженность поля сферы ведет себя иначе Нужно выбрать три возмодных варианта вспомогательных поверхностей , внутри сферы ( Внутри сферы нет зарядов то поток веткора напряденности поля равен 0 , Если выбрать поверхность равную =/>R , то содной стороны заряд равен жпсилон деленное на …. С другой- напраяжнности поля на площадь поверхности вспомогат. При р =>R это поле точченого щаряда располоден в центре этой поверхности , заряженной сферы Если < расстояние до выбранно точки радиуса заряден поля то напряженность – 0 Если расстояние ьольше иили равен радиусу сферы это уменьшаеся ……. Поле равномерно заряденной плоскости Плоскость не имеет толщины Чтобы это поле найти надо воспользоваться теорме гаусса Нажо выьрать поврхность вспомогат – цилиндр образущая которого паралельна нрмали к этой поверхности Плоклсть заряденно полодитльено то в обе стороны ………… Электрическое смещение Когда веткор эл.поля прохожит через границы диэлектриков этот вектор перетерпевает скачок , скачкообразно изменяется. При этом Напряженность электростатического поля зависит от свойства среды. Вектор переходя через границу диэлектриков, претерпевает скачок. Поэтому вводят новую величину, называемую электрическим смещением (электрической индукцией) Элетричская индукция – это произведени Поток вектора эл.смещения через проивзольную замкнутую поверхность равен алгебраической сумме зарядов заключенных внутри этой поверхности. Эл.смещение равен интегралу по обьему от объема Это 3 уравение Максвелла , постулат выраюазих закон эл.полей действием зарядов в среде По сути теорме гаусса уверждает что источником эл.поля являются эл.заряды Циркуляция вектора напряженности эл.поля Интеграл равен 0 Если циркуляция =0 , то поле потенциальное Н-р для магнитного поля , нулю не равна циркуляция |
