Уравнения параболического типа. Лекция 10 Уравнения параболического типа
 Скачать 62.29 Kb. Скачать 62.29 Kb.
|
|
Лекция 10 Уравнения параболического типа Ключевые слова: уравнения параболического типа, уравнение теплопроводности, уравнение диффузии, интеграл Фурье, одномерное уравнение, двумерное уравнение. Уравнения параболического типа получаются при исследовании таких физических явлений, как теплопроводность, диффузия, распространение электромагнитных полей в проводящих средах, движение вязкой жидкости. К уравнениям параболического типа относятся уравнения теплопроводности, уравнения диффузии. Они могут быть одномерными, двумерными или трехмерными, однородными или неоднородными. Одномерная задача о распределении температуры в стержне приводится к исследованию уравнения теплопроводности, которое в общем виде может быть представлено в виде: 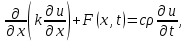 где 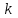 - коэффициент теплопроводности, зависящий от свойств материала, - коэффициент теплопроводности, зависящий от свойств материала,  - удельная теплоемкость и плотность вещества, - удельная теплоемкость и плотность вещества, 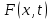 - функция плотности тепловых источников. - функция плотности тепловых источников. Если стержень однородный, это уравнение примет вид: 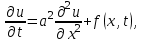 где 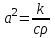 - коэффициент температуропроводности, - коэффициент температуропроводности, 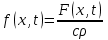 . .Если объемные источники тепла отсутствуют, то получим  Для нахождения единственного решения уравнения теплопроводности или диффузии необходимо задать начальные и граничные условия. Так как в уравнении теплопроводности содержится только первая производная по времени, начальное условие будет одно - оно будет определять значение искомой функции в начальный момент времени. Существует множество граничных условий. Основными видами являются граничные условия краевых задач первого, второго и третьего типа. Первая краевая задача поставлена, если на конце стержня поддерживается температура, изменяющаяся по определенному закону: 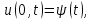 где 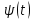 - заданная функция времени. - заданная функция времени.Вторая краевая задача поставлена, если на конце стержня задан тепловой поток 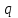 . Например: . Например: Тогда граничное условие примет вид: 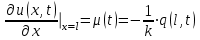 В случае теплоизолированного конца тепловой поток через него отсутствует и 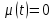 Третья краевая задача поставлена, если на конце стержня происходит теплообмен с окружающей средой. Граничное условие в этом случае имеет вид: 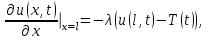 где 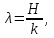 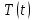 - температура окружающей среды, - температура окружающей среды, 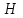 - коэффициент теплообмена. - коэффициент теплообмена.Также существуют и другие граничные условия. Например, если процесс теплопроводности изучается на ограниченном участке, находящемся достаточно далеко от концов стержня, что их влияние практически не будет сказываться, то стержень можно считать бесконечным и задать только начальное условие 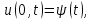 где 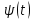 - заданная функция времени. - заданная функция времени.В случае, когда изучаемый участок стержня находится вблизи от одного его конца и далеко от другого конца, то можно ставить задачу для полубесконечного стержня, формулируя начальное и одно граничное условие. Можно рассмотреть еще один предельный случай, когда процесс теплопроводности изучается в течение длительного времени. В этом случае влияние начальных условий будет с течением времени ослабевать и распределение температуры будет определяться только граничными условиями. Рассмотрим простейший процесс такого типа – охлаждение бесконечного стержня. В начальный момент времени температура неравномерно нагретого длинного стержня задана функцией  . Требуется найти распределение температур для любого . Требуется найти распределение температур для любого  . Стержень очень длинный, поэтому температурные условия на его концах можно не учитывать. При отсутствии тепловых источников температура различных точек стержня определяется уравнением . Стержень очень длинный, поэтому температурные условия на его концах можно не учитывать. При отсутствии тепловых источников температура различных точек стержня определяется уравнением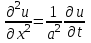 . .Для решения задачи воспользуемся методом разделения переменных. Представив решение в виде  , получим , получим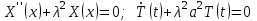 . . Решение этих уравнений имеет вид: 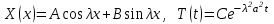 . .В результате получаем следующее семейство частных решений уравнения  . .Так как с течением времени температура стержня не может возрастать, показатель экспоненты в 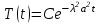 должен быть отрицательным. Следовательно, должен быть отрицательным. Следовательно, 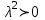 и и 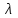 - вещественное число. Причем - вещественное число. Причем  . Чтобы получить решение, удовлетворяющее начальному условию, надо взять суперпозицию частных решений, соответствующих различным значениям . Чтобы получить решение, удовлетворяющее начальному условию, надо взять суперпозицию частных решений, соответствующих различным значениям 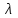 . Но так как в рассматриваемом случае . Но так как в рассматриваемом случае 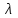 изменяется непрерывно, сумму нужно заменить интегралом: изменяется непрерывно, сумму нужно заменить интегралом: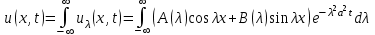 , ,Неизвестные функции 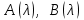 должны быть такими, чтобы выполнялось условие должны быть такими, чтобы выполнялось условие  : :  Это интеграл Фурье. Используя теорию интегралов Фурье, найдем 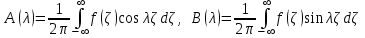 . . |
