Лекция №11. Лекция 11 Расчет сечений проводов по допустимой потере напряжения План. Общие положения методов
 Скачать 170.5 Kb. Скачать 170.5 Kb.
|
|
Лекция № 11 Расчет сечений проводов по допустимой потере напряжения План.
Общие положения методовСтрого говоря, методы выбора сечений по допустимой потере напряжения, разработаны для проводников, выполненнных из цветного металла в сети нап-ряжением до 35 кВ включительно. Методы разработаны исходя из допущений принятых в сетях такого напряжения. В основу методов определения сечения по допустимой потере напряжения положено то обстоятельство, что величина реактивного сопротивления проводни-ков x0 практически не зависит от сечения провода F:
Величина допустимой потери напряжения в ЛЭП рассчитывается по мощностям и сопротивлениям участков по формуле: 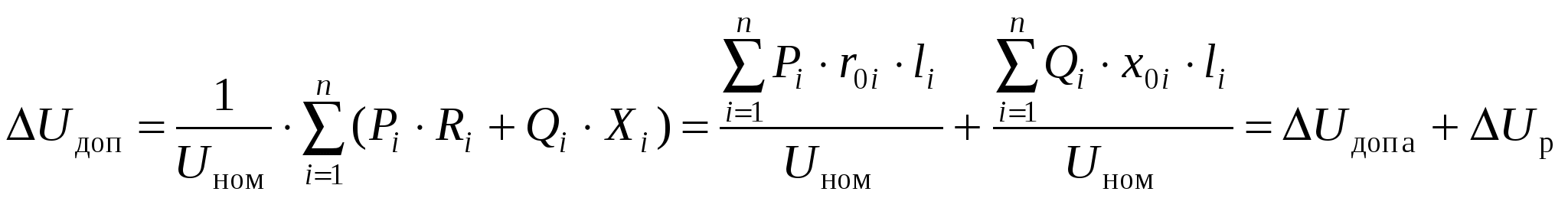 и складывается из двух составляющих – потери напряжения в активных сопротивлениях Учитывая обстоятельство, что x0 практически не зависит от сечения провода, величину По заданной величине допустимой напряжения в ЛЭП рассчитывают долю потери напряжения в активных сопротивлениях: В выражении для расчета потери напряжения в активных сопротивлениях от сечения зависит параметр где Если ЛЭП состоит только из одного участка, то величину сечения можно определить из выражения для При большем количестве участков ЛЭП, для расчета сечений проводников нужны дополнительные условия. Их три:
Расчет сечений проводов из условия постоянства сечений на участках Часто из практических соображений для однотипности проектируемой ЛЭП ее участки выполняют проводом одной марки. В этом случае формула для расчета величины потери напряжения в активных сопротивлених может быть представ-лена следующим образом: Откуда находится величина сечения провода: 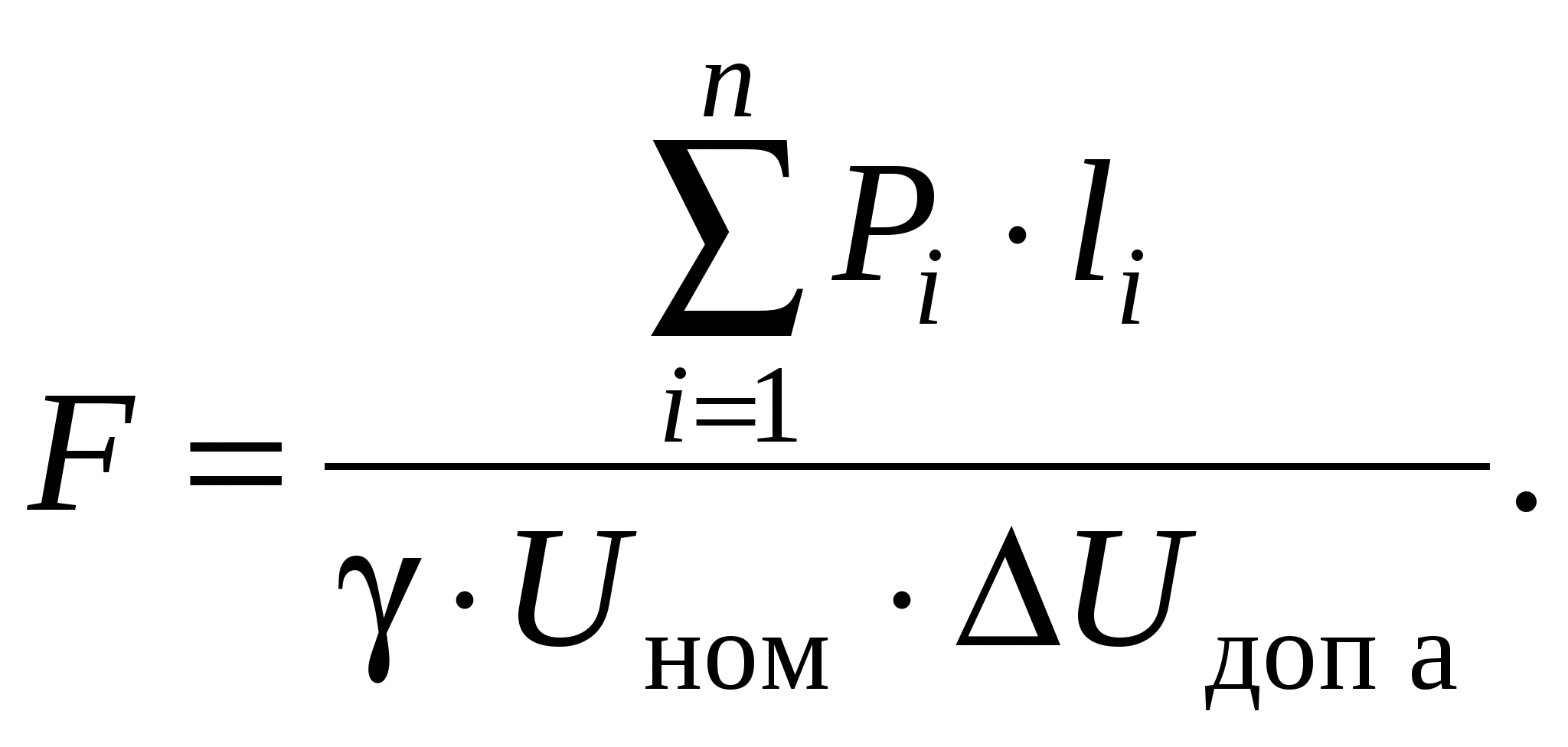 Полученную величину сечения округляют до ближайшего стандартного. Для него по справочнику определяют значения r0 и x0. Проверочным расчетом определяют действительную потерю напряжения и сравнивают ее с допустимой. Если действительная величина потери напряжения больше допустимой величины, то сечение увеличивают до следующего стандартного и расчет повторяют. Проверочный расчет не выполняется, если сечение округляют до ближайшего большего значения, а действительная величина x0 этого провода меньше x0 ср. Окончательно выбранное сечение проверяют по нагреву: Расчет сечений проводов из условия минимального расхода проводникового материала У ЛЭП, которые питают несколько потребителей, нагрузка уменьшается по мере удаления от источника питания. Применение на ЛЭП проводов одного сечения, хотя и выгодно в эксплуатационном и строительном аспектах, не всегда выгодно экономически. На последних участках провод всегда недогружен. Это приводит к перерасходу проводникового материала. Таким образом, необходимо знать как должны уменьшаться величины сечений по мере удаления от источника питания, чтобы не превысить величину Рассмотрим ЛЭП с двумя нагрузками (рис. 11.1). 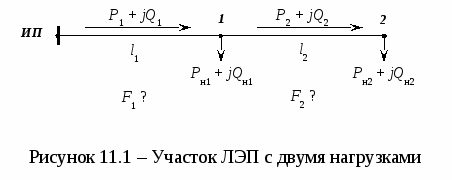 В приведенной сети известными являются:
Необходимо определить сечения проводов на участках из условия Мощности участков сети определяются по I закону Кирхгофа, начиная от конечной точки (точки 2): Задавшись x0ср, рассчитаем потерю напряжения в реактивных сопротивлениях: и долю потери напряжения в активных сопротивлениях: Предположим, что нам известна величина потери напряжения в активном сопротивлении 1-го участка В этом случае сечения на участках будут равны: Расход проводникового материала в сети на фазу составит: В этой формуле все величины известны, кроме 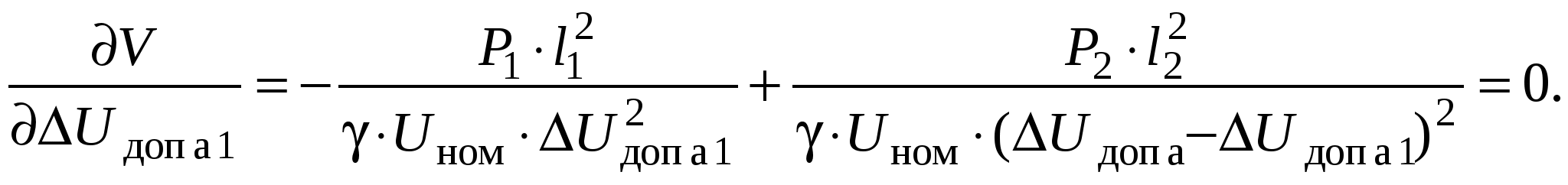 Получим равенство: 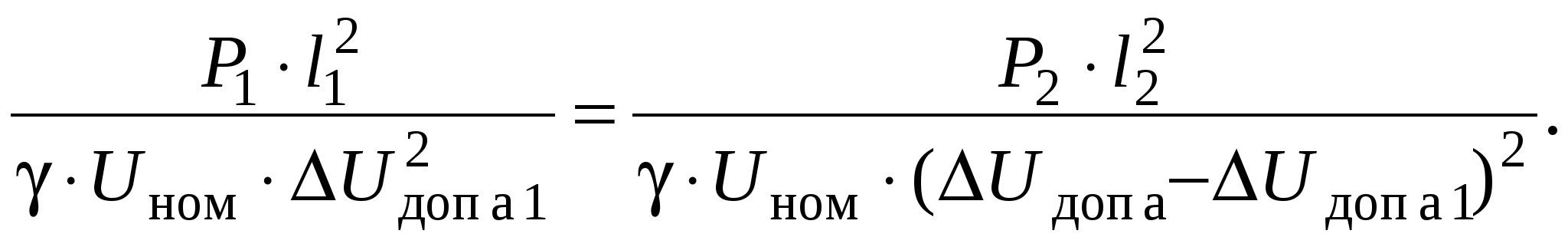 Умножим и разделим левую часть равенства на P1, а правую часть – на P2. Получим выражение: 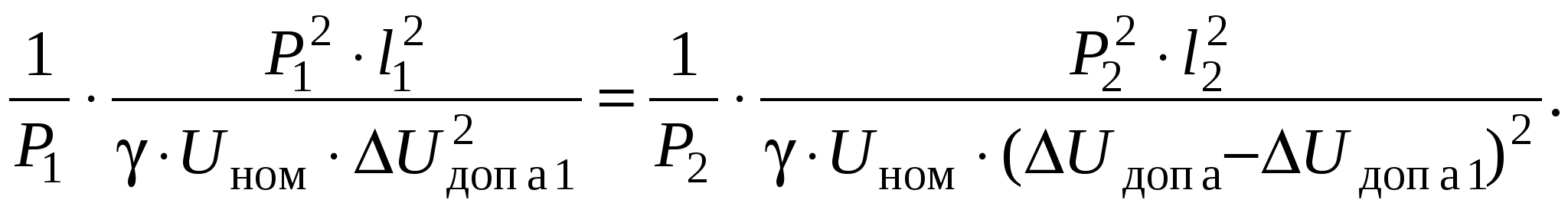 Умножим обе части равенства на 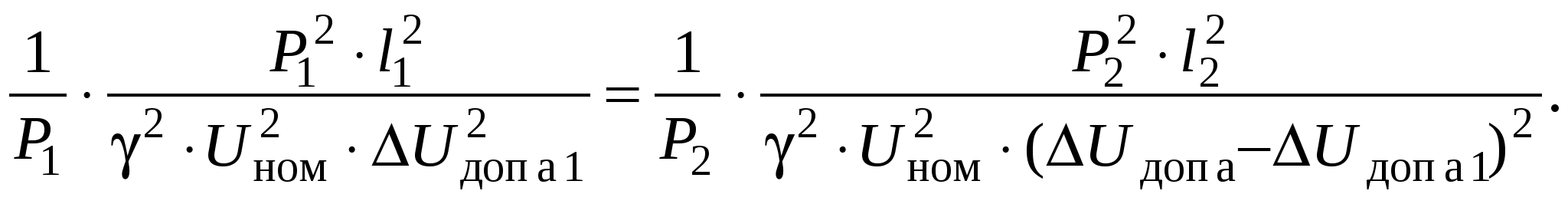 (11.1) (11.1)В этой формуле выражения 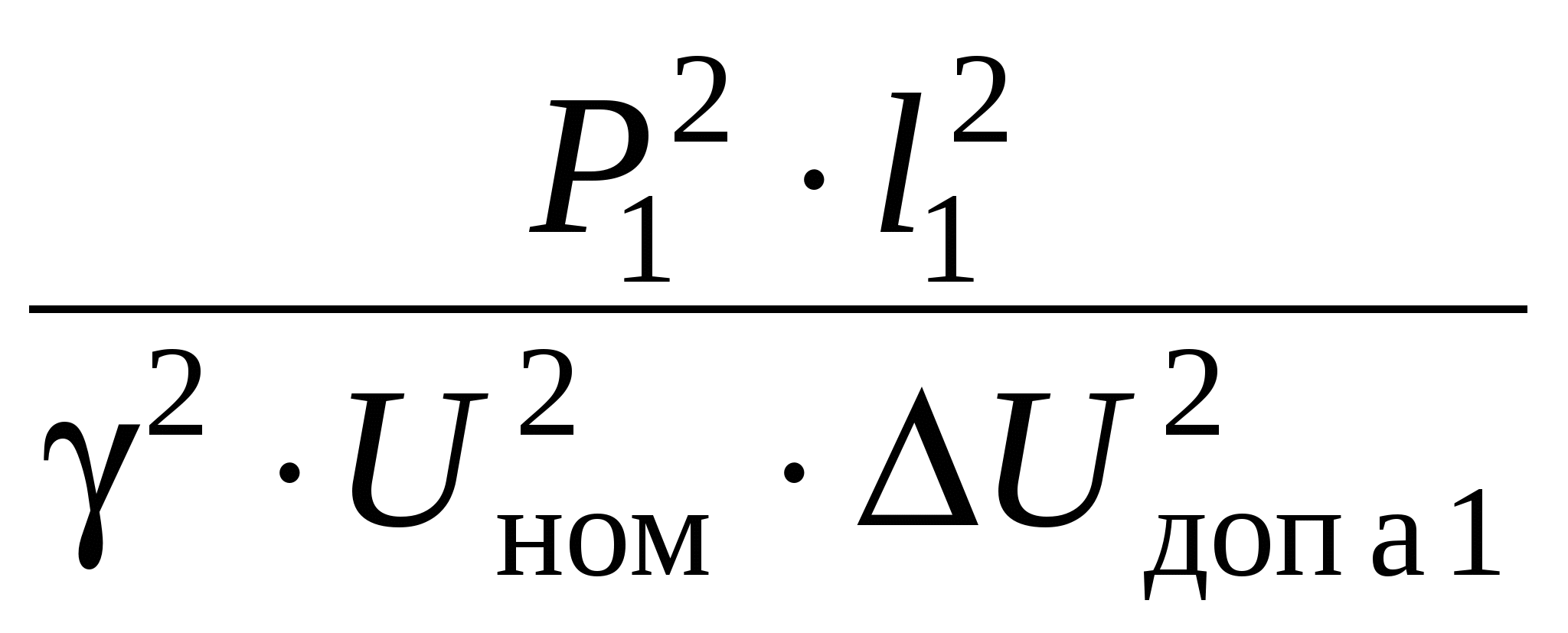 и и 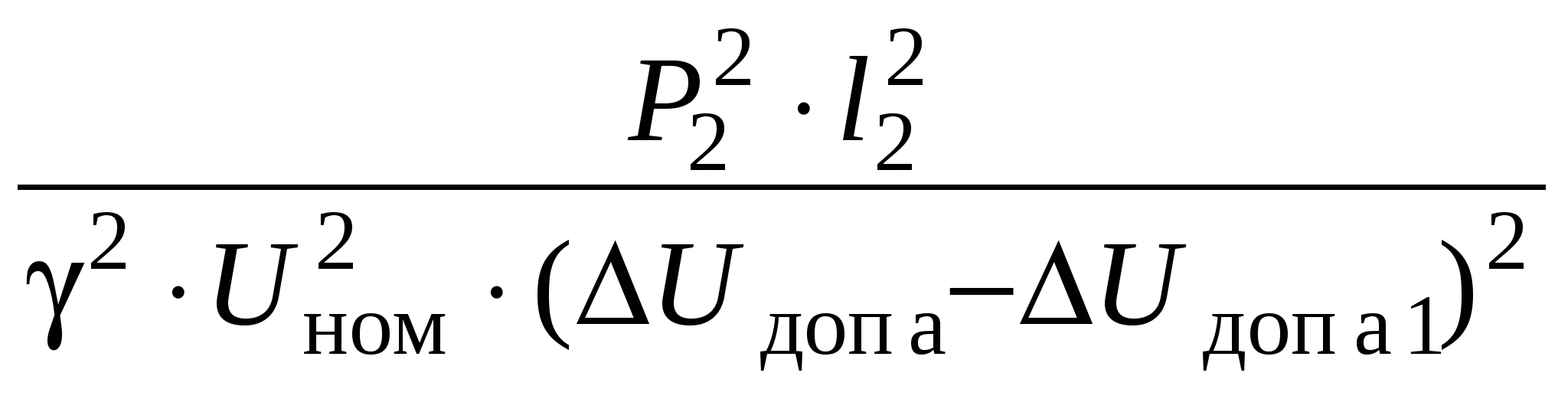 представляют собой квадраты сечений участков ЛЭП. Формулу (11.1) можно представить следующим образом: Таким образом, мы получили условие, при соблюдении которого при расчете сечений участков ЛЭП, потеря напряжения не превысит допустимой величины при минимальном расходе проводникового материала. Этот вывод можно распространить на любое количество участков ЛЭП. Величина 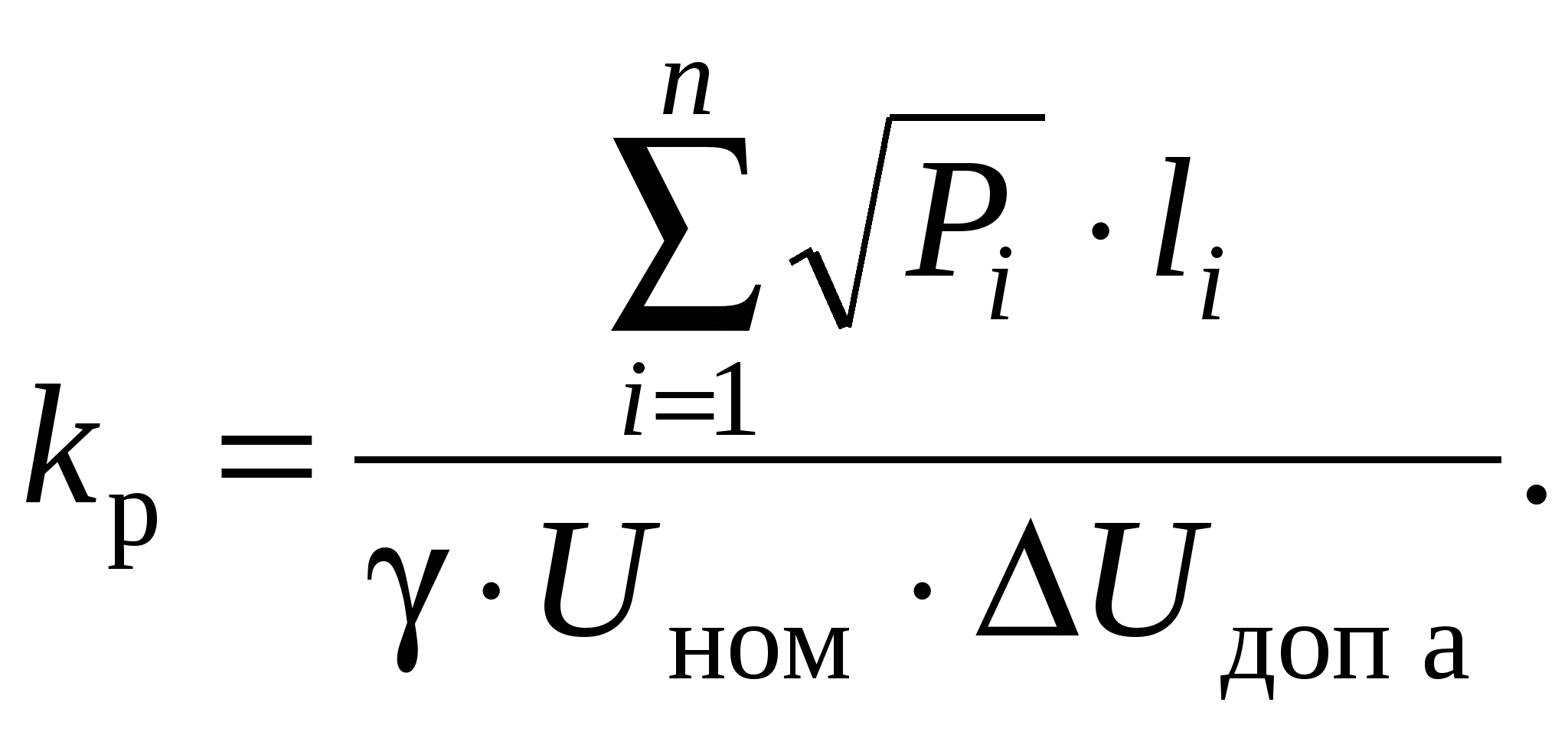 Зная величину kр, определяют сечение каждого участка ЛЭП: Сечения проводов округляют до ближайших стандартных и проверяют по потере напряжения и нагреву. Если сечения не удовлетворяют допустимой потере напряжения, то увеличивают сечения на тех участках, величина потери напряжения на которых наибольшая. Расчет сечений проводов из условия минимума потерь мощности в сети Сечения проводов, выбранные по условию минимума расхода проводникового материала, не обеспечивают минимальных потерь мощности. Найдем сечения проводов, которые отвечают условию Для ЛЭП, приведенной на рис. 11.1, потери активной мощности рассчитываются по формуле: 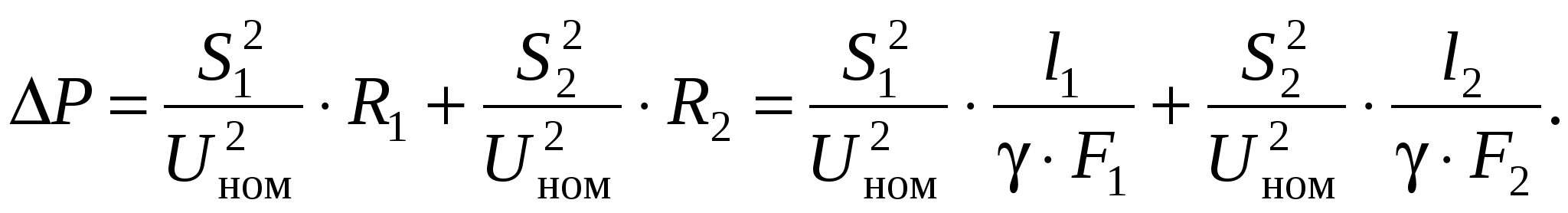 (11.2) (11.2)Обозначим объем проводникового материала одной фазы на всей ЛЭП через V, на первом участке – V1. Тогда величины сечений участков будут равны: Подставим эти выражения в формулу (11.2) и получим: 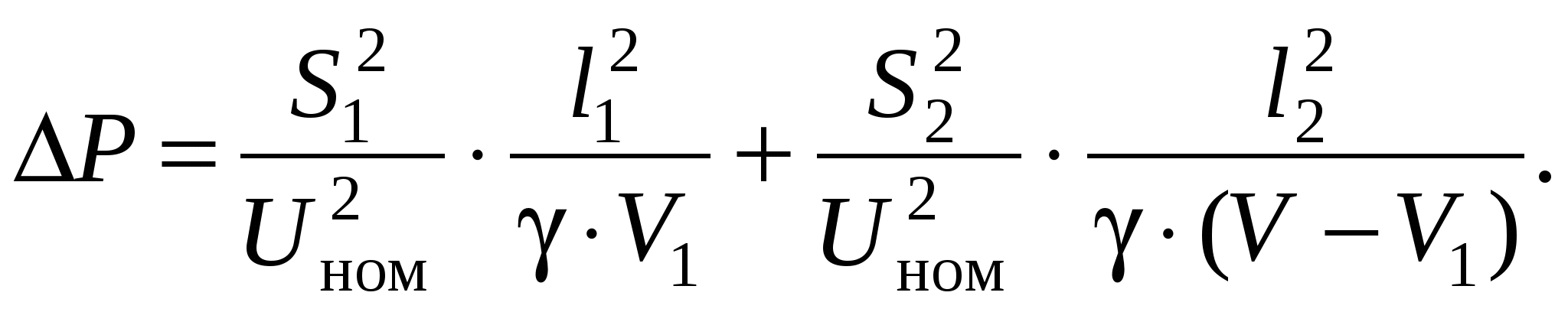 В этой формуле все величины известны, кроме V1. Для определения минимума потерь активной мощности необходимо взять частную производную по неизвестной величине и приравнять ее к нулю: 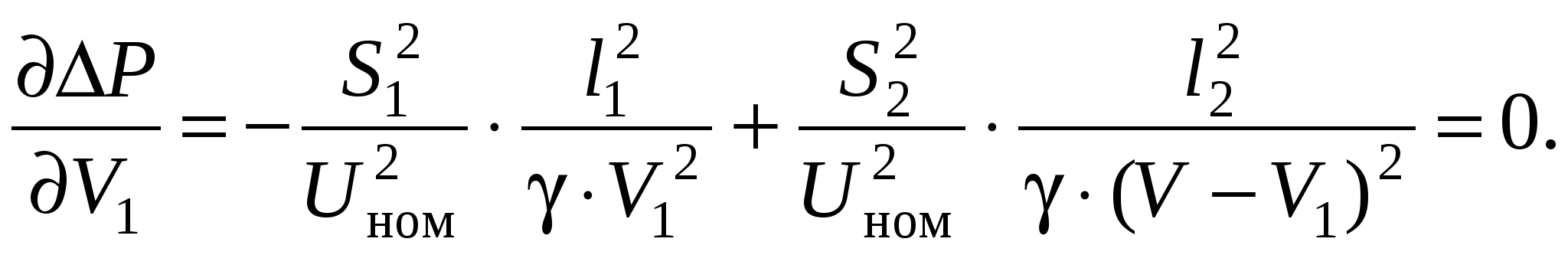 Получим равенство: 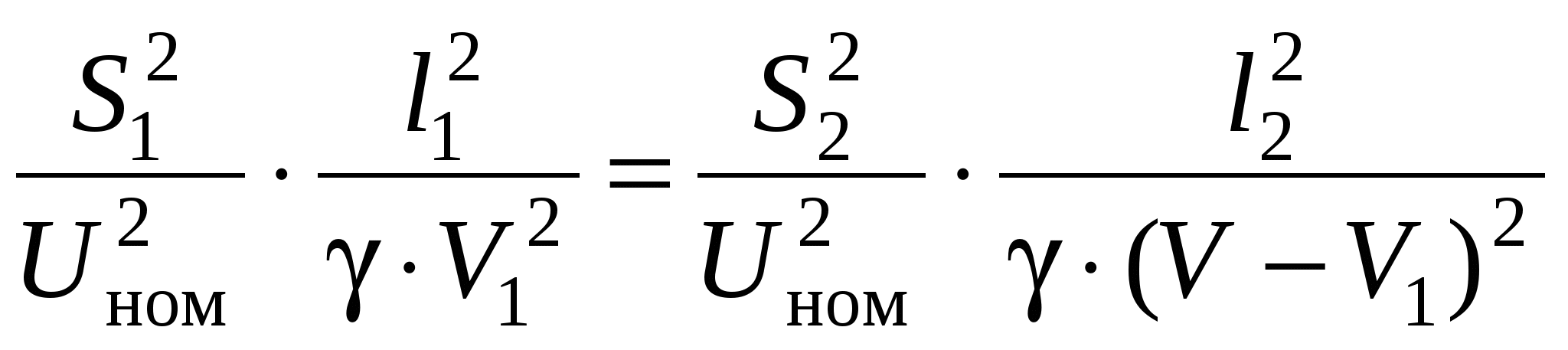 . .Сократим полученное выражение на 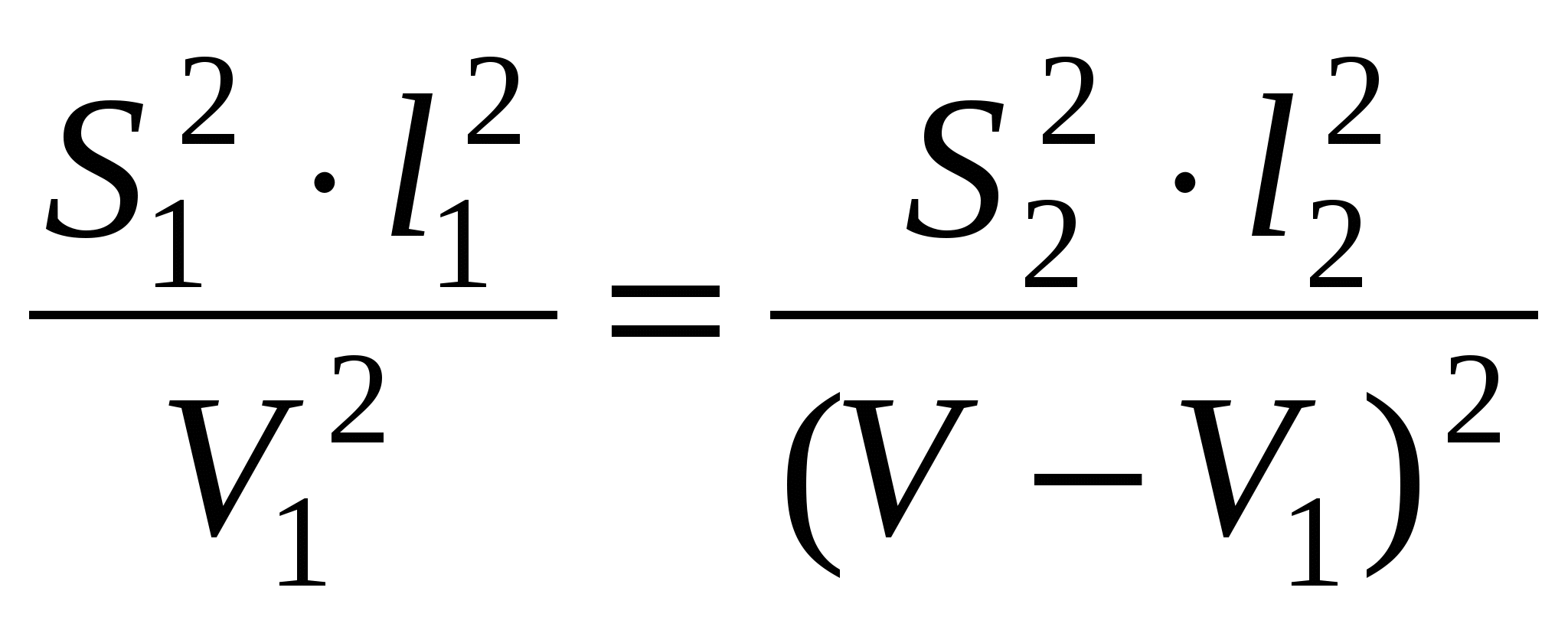 . (11.3) . (11.3)Так как 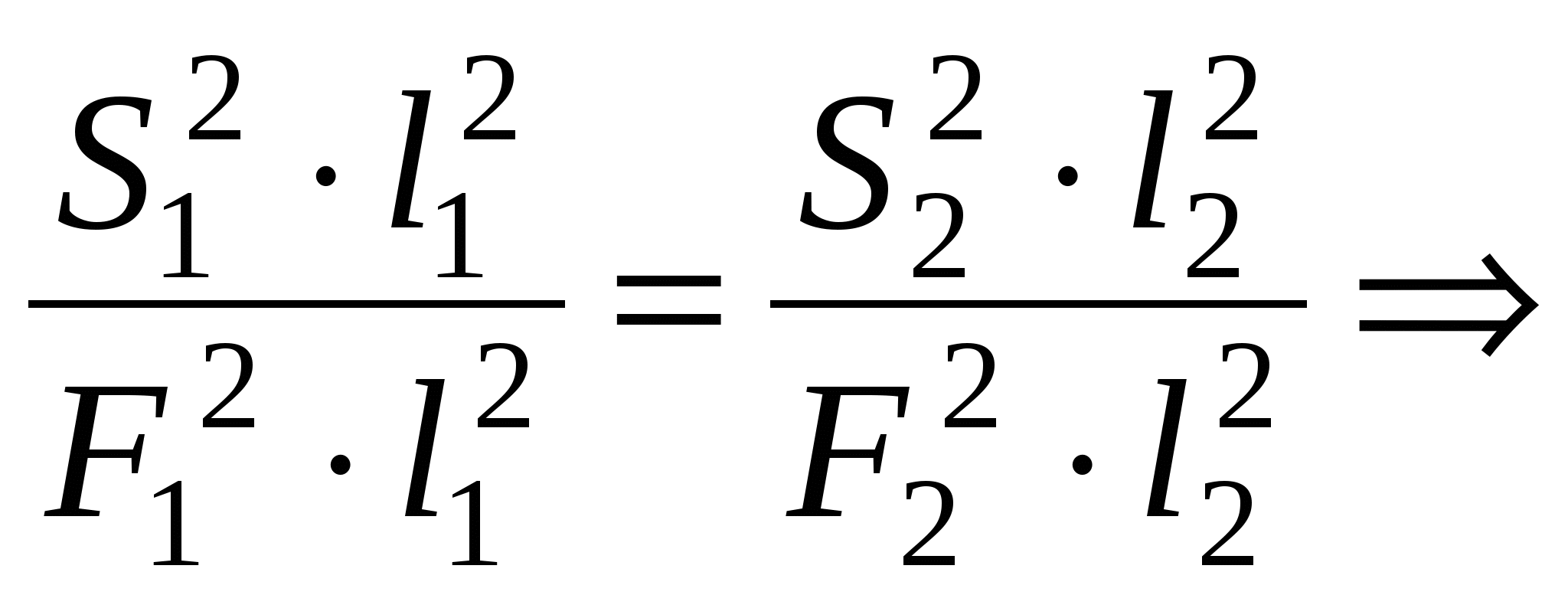 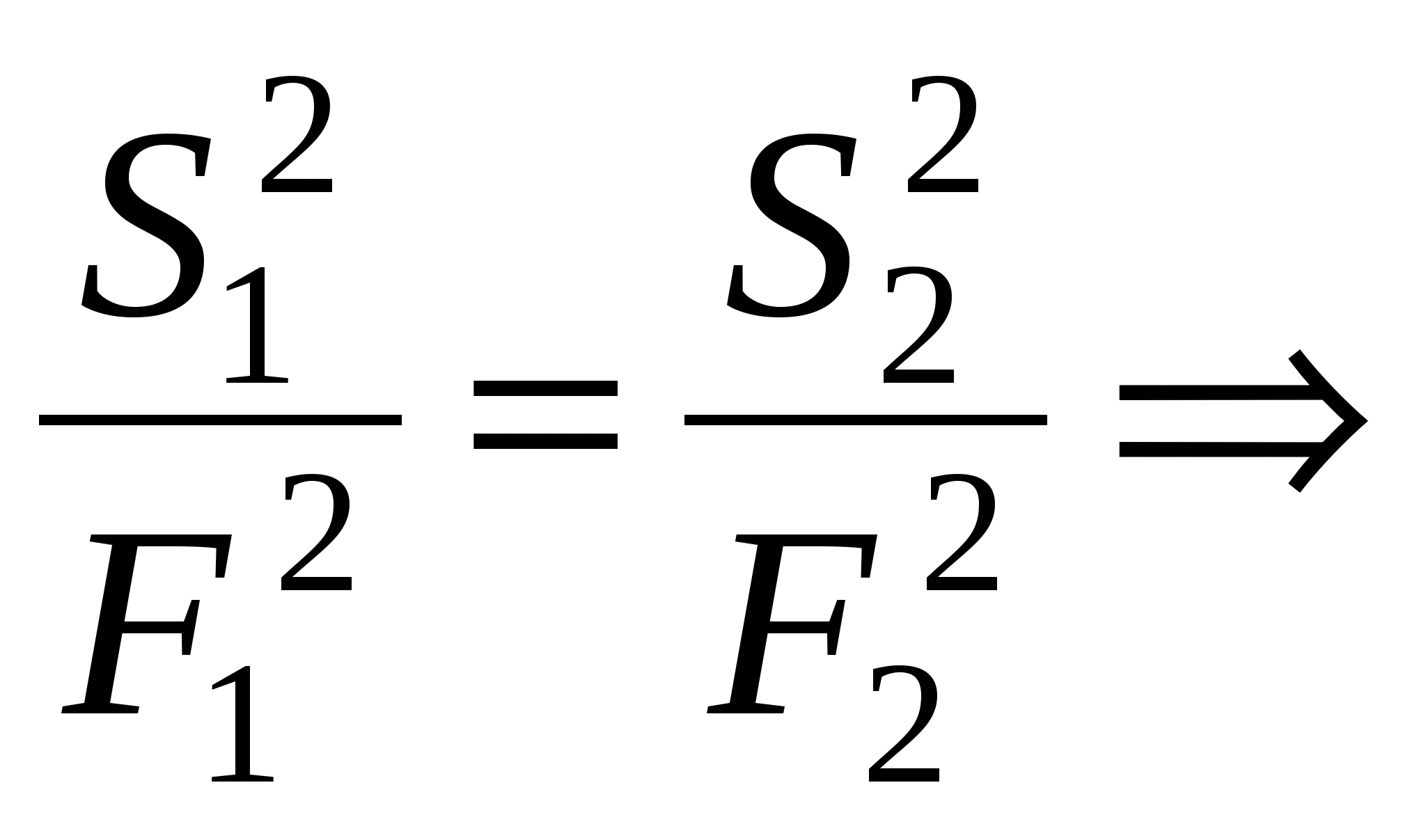 Выразим мощности участков через токи и номинальное напряжение ЛЭП: Отношение тока к сечение называется плотностью тока Значение плотности тока 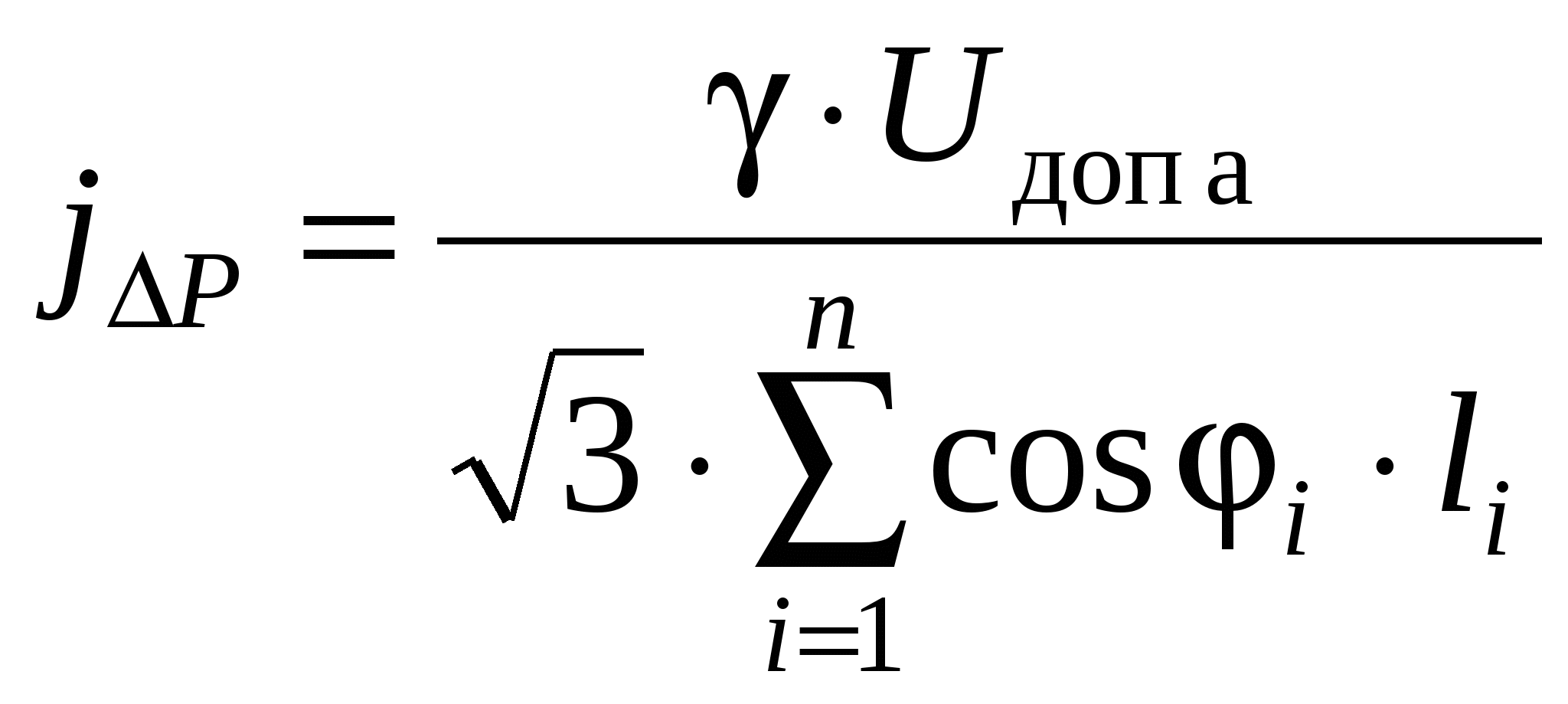 . .Сечения на участках рассчитываются по токам участков: где Сечения проводов округляют до ближайших стандартных и проверяют по потере напряжения и нагреву. Если сечения не удовлетворяют допустимой потере напряжения, то увеличивают сечения на тех участках, величина потери напряжения на которых наибольшая. Этапы расчета при разных условиях Выбор сечений по допустимой потере напряжения выполняется по следующему алгоритму:
5.1 постоянство сечений на всех участках: F=…; 5.2 минимальный расход проводникового материала: kр = … → F=…; 5.3 минимальные потери активной мощности:
Сравнительная характеристика методов Определение сечения по допустимой потере напряжения применяют к линиям местных сетей, сечения которых не выбирают по экономической плотности тока. Выбор сечения по условиям минимального расхода проводникового материала ( Выбор сечения при условии Выбор сечения по экономической плотности тока учитывает оба фактора. Поэтому метод является основным. Если длина ЛЭП велика, то сечение, выбранное по экономической плотности тока jэк, может не обеспечить допустимую потерю напряжения. Это приводит к необходимости пересчета сечения. Поэтому нужно сначала определить плотность тока из условия допустимой потери напряжения |
