Лекция 1. Лекция 12 Занятие Вязкость. Поверхностное натяжение. Давление насыщенного пара жидкости. Растворение газов в жидкости. Порог кавитации
 Скачать 192.86 Kb. Скачать 192.86 Kb.
|
1.3. Капельные и некапельные жидкостиВ гидравлике, в основном, считается, что жидкость практически не изменяет свой объем под действием внешних сил, т.е. является несжимаемой. К несжимаемым жидкостям относятся все капельные жидкости: вода, нефть, мазут. В отличие от капельных жидкостей, газы (воздух, пропан, бутан и т.д.) легко изменяют объем под действием внешних сил, сжимаются, поэтому их называют сжимаемыми. Любая капельная жидкость может переходить в газообразное состояние при определенной температуре и давлении. Соответственно, газы при понижении температуры и повышении давления могут переходить в жидкое состояние. 1.4. Силы, действующие в жидкостиНа произвольно выделенный объем жидкости действуют два вида сил: Поверхностные: Р – сила давления Т – сила трения Массовые: G – сила тяжести I – сила инерции Массовые силы действуют по всему выделенному объему и пропорциональны его массе G = mg I, =−ma . Поверхностные силы действуют по поверхности и пропорциональны площади поверхности. Рассмотрим подробно поверхностные силы. Под влиянием внешних сил, действующих на выделенный объем возникают соответствующие внутренние силы. Проведем внутри объема поверхность S, разделяющую его на две части I и II (см. рис. 1.1). Отбросим часть II и для сохранения равновесия введем силы такие же, как и силы с которыми часть II действовала на часть I. На элементарную площадку Δs разделяющей поверхности действует сила Δf. Площадь Δs может быть стянута в точку М с координатами x, y, z. В этом случае площадь поверхности Δs, так и сила Δf стремится к нулю. Отношение силы df к площади поверхности ds стремится к пределу, 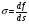 который называют напряжением. который называют напряжением. df N II I df T ds Рис . 1.1. Напряжение в жидкости Силу df, действующую на площадь ds можно разложить на две составляющие: тангенциальную и нормальную. Соответственно, напряжение в жидкости может быть тангенциальным (τ) и нормальным (p). Тангенциальное напряжение, действующее вдоль поверхности ds, называют напряжением трения. 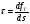 (1.1) (1.1)где dfT – сила трения площади ds. Нормальное напряжение, действующее по нормали к поверхности ds, называют напряжением давления или давлением  (1.2) (1.2)где dfN – сила давления площади ds. Для площади S можно записать  (1.3) (1.3)где Т – сила трения площади S. 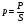 (1.4) (1.4)где Р – сила давления площади S. В покоящейся жидкости имеется только нормальное напряжение, тангенциальное напряжение отсутствует. Сила трения действует вдоль поверхности: T =τS . (1.5) Сила давления направлена по нормали к поверхности: P = pS . (1.6) 1.5. Давление и его свойстваВ любой точке жидкости имеется давление и его можно измерить, опустив в жидкость стеклянную трубочку с запаянным концом из которой выкачен воздух. Рассмотрим точку М в жидкости, проведем через эту точку поверхность ds (рис. 1.2). Результирующая сила воздействия всех молекул, находящихся в постоянном движении, на эту поверхность перпендикулярна ds. Можно записать в векторной форме dfN = pdsn,где n – единичный вектор, направленный по нормали к поверхности ds. ds M n fN Рис. 1.2. Давление в точке dfN зависит от величины поверхности ds, но из формулы видно, что давление в точке не за- висит от ds. Свойства давления:
p = f x y z( , , ). (1.7) Понятие о градиенте давления. Рассмотрим точку М, имеющую координаты (x, y, z) и находящуюся в жидкости(рис. 1.3). Давление в точке М – pM . Это давление зависит только от координат точки М. Можно записать pМ = р(x y z, , ). На небольшом расстоянии от точки М находится точка М1с координатами (x+dx, y+dy, z+dz). Давление в М1 отличается от давления рМ на некоторую величину dp: pM1 = pM + dp. Давление pM1 зависит от координат точки М1: рМ1 = р(x + dx y, + dy z, + dz). Тогда dp = р(x + dx y, + dy z, + dz)− р(x y z, , ). 1 M M j k i x y z Рис . 1.3. Градиент давления Т.к. р является функцией координат x, y, z, то величину dp можно записать в дифференциальной форме ∂p ∂p ∂p dp = dx + dy + dz. ∂x ∂y ∂z Вектор перемещения от точки М к точке М1 записывается в форме MM 1 = idx + jdy + kdz, где i , j, k – единичные векторы, направленные вдоль осей координат. Определение: В физике для обозначения изменения некоторой скалярной величины G (температуры, давления) от одной точки к другой используется понятие вектора
∂G∂G ∂G dx dy dz или dp = gradpMM 1 . Вывод: изменение давления dp является скалярным произведением двух векторов grad p и ММ1. Свойства вектора gradp:
рМ = рМ1 , тогда dp = 0. Вывод: gradp расположен по нормали к поверхности равного давления, проходящей через точку М.
тельное значение и gradp имеет то же направление, что и ММ1. Вывод: gradpнаправлен в сторону увеличения давления. dp
Вывод: величина gradp определяется отношением разности давлений в двух точках к расстоянию между этими точками. Единицы давления. При измерении атмосферного давления используют единицу давления – бар
При измерении при помощи пьезометрических трубок используют единицы длины
Можно подсчитать, что: 1 бар = Старая система измерения. Давление, создаваемое телом массой 1 кг на 1 см2: 1Кгс/ см2 = 0,98 бар. 1.6. Основные физические свойства жидкостейПлотность – масса жидкости m, заключенная в единице объема V ρ = m/ V (1.11) Плотность меняется при изменении температуры и давления. Удельный вес – вес жидкости G в единице объема V γ = G/ V (1.12) Плотность и удельный вес связаны между собой соотношением γ = g‧ ρ (1.13) Сжимаемость – свойство жидкостей изменять объем при изменении давления. Сжимаемость капельных жидкостей характеризуется коэффициентом объемного сжатия, который представляет собой относительное изменение объема жидкости на единицу изменения давления 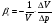 (1.14) (1.14)где V – первоначальный объем жидкости; Знак «минус» в формуле обусловлен тем, что положительному приращению давления р соответствует отрицательное приращение (уменьшение) объема. Величина, обратная коэффициенту объемного сжатия называется модулем упругости E0 =1/ βV (1.15) В качестве примера, приведем значения модуля упругости стали и воды: Еводы = 2×109Па, Естали = 2 ×1011Па . Таким образом, мы видим, что упругость воды всего только в 100 раз меньше упругости стали, значит, воду можно рассматривать как несжимаемое вещество. Коэффициент объемного сжатия и модуль упругости капельных жидкостей практически не изменяется при изменении давления, и на практике очень часто их считают неизменными. Част при расчетах коэффициент объемного сжатия βV воды принимают постоянным и равным 0,49×10–9 Па–1. Сжимаемость характеризуется также отношением изменения давления к изменению плотности, равным квадрату скорости распространения звука в среде: a 2= dp / dρ (1.16) Очевидно, для малосжимаемой среды при больших изменениях давления изменение плотности незначительно и скорость звука получается большой, и наоборот, при большой сжимаемости скорость звука оказывается малой (для воздуха – 330 м/с). Для оценки сжимаемости среды при ее движении важно не абсолютное значение скорости звука а, а относительное, которое называется числом Маха: Ма = u/a. Если скорость движения воздуха мала по сравнению со скоростью движения звука в ней, число Маха мало по сравнению с единицей и движущуюся среду можно рассматривать как несжимаемую жидкость. Скорость воздуха в воздуховодах, газа в газопроводах низкого давления и газоходах котельных установок не превышает 12 м/с. Следовательно, в практике теплоснабжения и вентиляции газ(воздух) можно рассматривать как несжимаемую жидкость. При движении газов со скоростью более 70 м/с влияние сжимаемости следует учитывать. В отличие от капельных жидкостей газы характеризуются значительной сжимаемостью и высокими значениями коэффициента температурного расширения. Зависимость плотности газов от давления и температуры устанавливается уравнением состояния. Для совершенных газов (нет взаимодействия между молекулами) справедливо уравнение Клапейрона, позволяющее определить плотность газа при известных давлении и температуре ρ = p/ RT (1.17) где р – абсолютное давление; R – удельная газовая постоянная (для воздуха R= 287 Дж/кг·К); Т – абсолютная температура. В технических расчетах плотность газа, приводят к нормальным физическим условиям (t = 0ºC; p = 101325 Па) или стандартным условиям (t = 20ºC; p = 101325 Па) Можно подсчитать, что в стандартных условиях плотность воздуха ρ= 1,21 кг/м3. При других условиях плотность воздуха можно определить по формуле 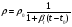 (1.18) (1.18)где ρ0,Т0и р0 – плотность, температура и давление при известных стандартных условиях соответственно. Сжимаемость газа зависит от характера процесса изменения состояния. Для изотермического процесса сжимаемость воздуха составляет примерно 9,8×104 Па, что превышает в 20000 раз сжимаемость воды. Температурное расширение – увеличение объема капельных жидкостей, при увеличении температуры, характеризуется коэффициентом температурного расширения βt , выражающим относительное увеличение объема жидкости при увеличении температуры на 1 град.  (1.19) (1.19)где ΔV – изменение объема при повышении температуры на величинуΔt . Если считать, что плотность не меняется при изменении давления, а только от температуры, то для расчета изменения плотности капельных жидкостей с изменением температуры можно использовать формулу 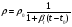 (1.20) (1.20)где ρ0 – плотность при известной температуре t0 . Поверхностное натяжение. Капиллярные явления. Молекулы жидкости, находящиеся у поверхности контакта с другой жидкостью, газом или твердым телом имеют другую энергию, чем молекулы, находящиеся внутри объема жидкости. Эта энергия пропорциональна площади поверхности раздела S и характеризуется величиной коэффициента поверхностного натяжения σ, который зависит от материала соприкасающихся сред, чистоты поверхности и температуры. На поверхности раздела трех фаз (рис. 1.4): твердой стенки, жидкости и газа образуется краевой угол θ. Величина угла зависит только от природы соприкасающихся сред, и не зависит от формы сосуда и силы тяжести. Чем хуже смачивающая способность, тем больше краевой угол. От явления смачивания зависит поведение жидкости в тонких (капиллярных) трубках, погруженных в жидкость. При плохом смачивании жидкость в трубке поднимается над уровнем свободной поверхности, при хорошем – опускается.  θ θθ Рис. 1.4. Капиллярные явления Влияние сил поверхностного натяжения приходится учитывать при работе с жидкостными приборами для измерения давления, при истечении жидкости из малых отверстий, при фильтрации, в других случаях, когда силы, действующие в жидкости меньше сил капиллярного натяжения. Пенообразование. Для пенообразования необходимо, чтобы в жидкости находились смачивающие вещества, которые уменьшают поверхностное натяжение. Смачивающие вещества состоит из двух групп: гидрофильной и гидрофобной. Они создают пену, которая представляет множество пузырьков воздуха. Пенообразующие добавки используются при изготовлении ячеистого бетона. Растворимость газов в жидкостях – способность жидкостей растворять в своем объеме газы. Количество растворенного газа в единице объема жидкости различно для разных жидкостей и изменяется с изменением давления. Относительный объем газа, растворимого в жидкости до ее полного насыщения прямо пропорционален давлению:  (1.21) (1.21)гдеVг – объем растворенного газа при нормальных условиях; Vж – объем жидкости; к – коэффициент растворимости; р1и р2 – начальное и конечное давление. При понижении давления в жидкости происходит выделение растворенного в ней газа. Выделение происходит интенсивнее, чем поглощение. Растворимость необходимо учитывать при расчете работы машин и систем высокого давления, при расчете кавитации. Давление насыщенного пара. При определенных условиях капельные жидкости превращаются в пар и наоборот. Изменение агрегатного состояния зависит от давления паров жидкости, насыщающих пространство над ней при данной температуре. Интенсивное выделение пара по всему объему жидкости называется кипением. Температура кипения зависит от давления на поверхности жидкости. Таким образом, интенсивное выделение пара (кипение) может происходить при низких температурах, если давление на поверхности пониженное. Это необходимо учитывать при анализе работы водопроводных систем на участках пониженного давления. Таблица 1.1
1.7. Вязкость. Идеальная жидкостьВязкость– свойство жидкостей оказывать сопротивление сдвигу соседних слоев при движении жидкости. Все реальные жидкости обладают вязкостью, которая проявляется в виде внутреннего трения при относительном перемещении смежных частей жидкости. Свойство, обратное вязкости – текучесть. Текучесть характеризует степень подвижности частиц жидкости. На рис. 1.5 представлена эпюра скорости вязкой жидкости, движущейся в цилиндрической трубе. Вследствие тормозящего влияния стенки слои жидкости будут двигаться с разными скоростями, значения которых возрастают по мере отдаления от стенки. Рассмотрим два слоя жидкости, движущиеся на расстоянии Δy друг от друга. Слой А движется со скоростью u, а слой B со скоростью u +Δu . Вследствие разности скоростей слой В сдвигается относительно слоя А на величину Δu , которая является абсолютным сдвигом слоя А по слою В, а Δu /Δy– относительный сдвиг или градиент скорости. Если расстояние между слоями будет мало, то градиент скорости можно записать как du /dy . Можно также сказать, что градиент скорости показывает интенсивность изменения скорости в данном сечении. В результате сдвига соседних слоев появляется касательное напряжение трения. Δ y Δ u A B Рис.1.5. Распределение скоростей в сечении трубы при ламинарном движении Согласно гипотезе Ньютона, касательное напряжение, возникающее при движении жидкости пропорционально скорости деформации объема жидкости  (1.22) (1.22)где μ – коэффициент пропорциональности или динамический коэффициент вязкости. Единица измерения динамического коэффициента вязкости – Пуаз (П) 1П= 0,1 Па·с = 0,0102 кгс с⋅/ м2 . Вязкость капельных жидкостей с увеличением температуры уменьшается, а газов увеличивается. Это связано с различным молекулярным строением жидкостей и газов. Для определения вязкости при различных температурах используются эмпирические формулы, значения вязкости для различных жидкостей приводятся в справочниках. Например, вязкость воды при температуре 20 ºC равна 0,01П. Наряду с понятием динамической вязкости в гидравлике применяется кинематическая вязкость ν, которая представляет собой отношение динамической вязкости жидкости к ее плотности  (1.23) (1.23)Единицы измерения – Стокс (Ст): 1Ст=1см2/с Для определения кинематической вязкости при различных температурах также используются эмпирические формулы, и ее значения для различных жидкостей приводятся в справочниках. Кинематическая вязкость воды при температуре 20ºC равняется 0,01 . см2/с Вязкость капельных жидкостей мало зависит от давления в диапазоне до 200 атм. Кинематическая вязкость воздуха (газов) зависит и от давления, и от температуры. Для нормальных условий (t = 20 ºC, p = 100000 Па) νвоздуха = 0,157 см2/с , т.е. почти в 15 раз больше воды, что связано с меньшей плотностью воздуха. Измерение вязкости проводится при помощи специальных приборов, называемых вискозиметрами. Измерение вязкости вискозиметром Энглера студенты выполняют во время лабораторных работ. Идеальная жидкость – жидкость, в которой отсутствует вязкость. Представляет собой модель реальной жидкости, и это понятие используется для облегчения решения некоторых задач гидравлики. Выводы, полученные исходя из свойств невязкой жидкости, приходиться корректировать, вводя поправочные коэффициенты, получаемые в результате экспериментальных исследований. |
