Лекция№17-тпр (1) 2.10.14. Лекция№17-тпр (1) 2.10. Лекция 17. Решение матричной игры () среди смешанных стратегий. Теорема об активных стратегиях
 Скачать 0.54 Mb. Скачать 0.54 Mb.
|
|
Лекция №17. Решение матричной игры ( Игры ( При использовании смешанной стратегии перед каждой партией игры пускается в ход какой-то механизм случайного выбора, обеспечивающий появление каждой стратегии с некоторой вероятностью, и затем принимается стратегия, на которую пал жребий. Смешанные стратегии представляют собой математическую модель гибкой тактики, при которой противник не знает и не может узнать заранее с какой обстановкой ему придется встретиться. Пусть имеется игра ( 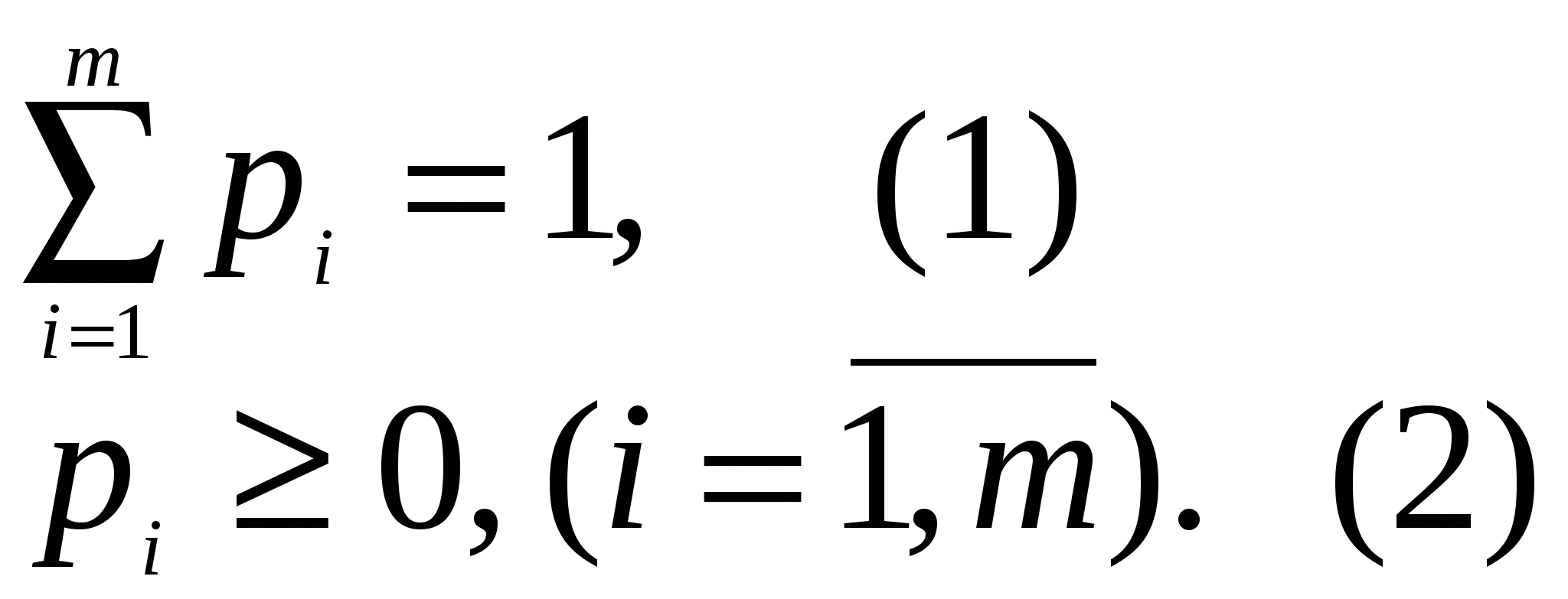 Смешанную стратегию игрока 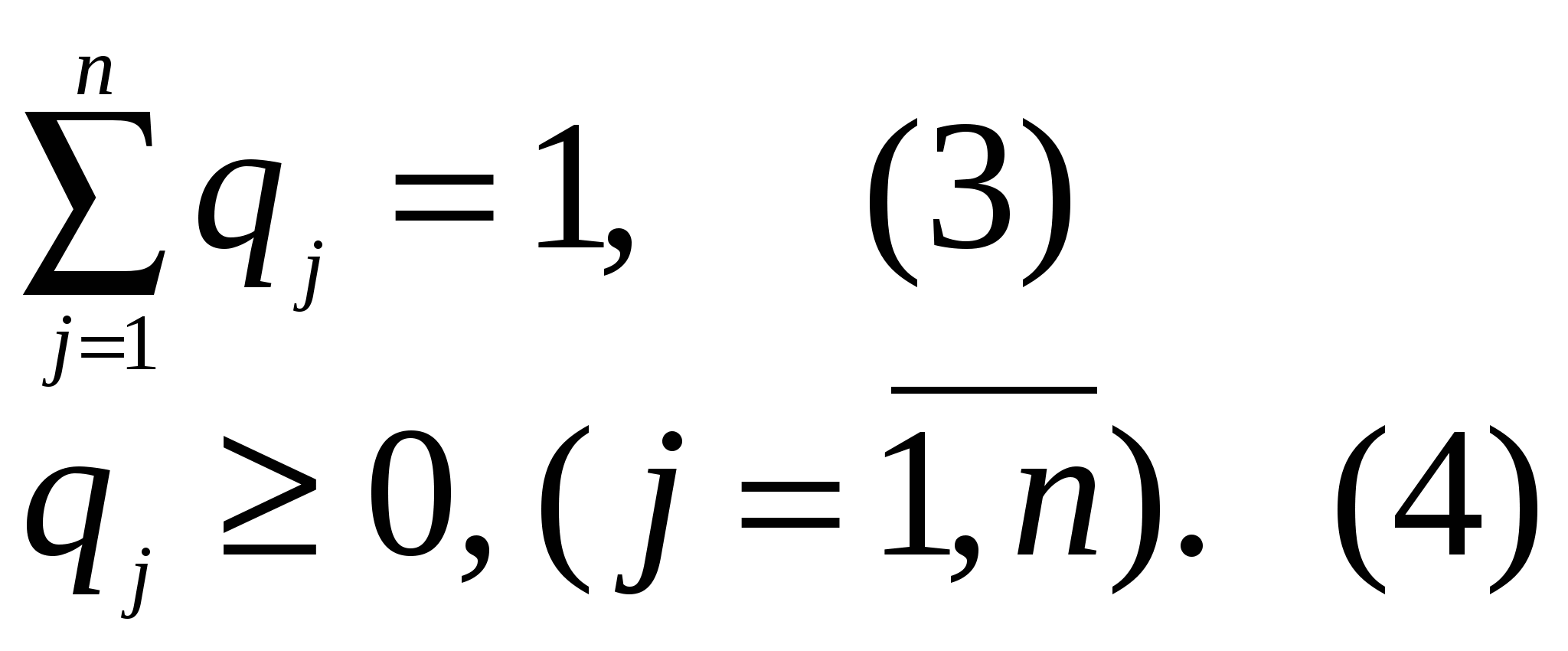 Отметим, что смешанных стратегии бесчисленное множество, так как вероятностей Поскольку игроки в партии применяют стратегии случайным образом, то и исход партии будет случайным. Допустим игроки Пусть оптимальными смешанными стратегиями игроков Пара смешанных стратегий ( Из определения оптимальной пары ( И 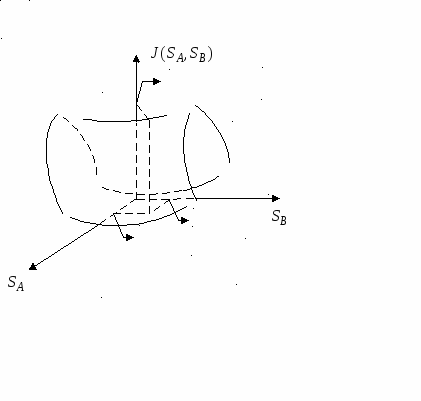 з этого неравенства вытекает, что оптимальная пара ( Теорема об активных стратегиях. Применение оптимальной смешанной страте6гииобеспечивает игроку максимальный средний выигрыш (или минимальный средний равный цене игры Доказательство. Пусть найдено решение игры ( Для найденных вероятностей справедливы равенства Выигрыш игрока Выразим теперь цену игры Основная теорем теории игр. Любая конечная парная игра с нулевой суммой имеет по крайней мере одно решение, возможно в смешанных стратегиях. Определение оптимальных смешанных стратегий. В предыдущей лекции было показано, что если матричная игра ( Процесс отыскания оптимальных смешанных стратегий Определение1. Если в матрице Доказательство. Пусть найдено решение игры ( Очевидно Пусть игрок Учитывая неравенство (8) можно равенство (7) записать: Соотношение (9) выполнимо только тогда, когда неравенства (8) превращаются в равенства. Отсюда следует, что для любой смешанной стратегии Определение2. Если в матрице Определение3. Если в матрице Естественно, если для какой-то стратегии есть доминирующая или дублирующая стратегии, то их не рассматривают. Это позволяет уменьшить размерность пары ( Пример. Имеется игра (
Пусть теперь имеется парная конечная игра ( ( Сначала найдем оптимальную смешанную стратегию Допустим, игрок Поскольку игрок 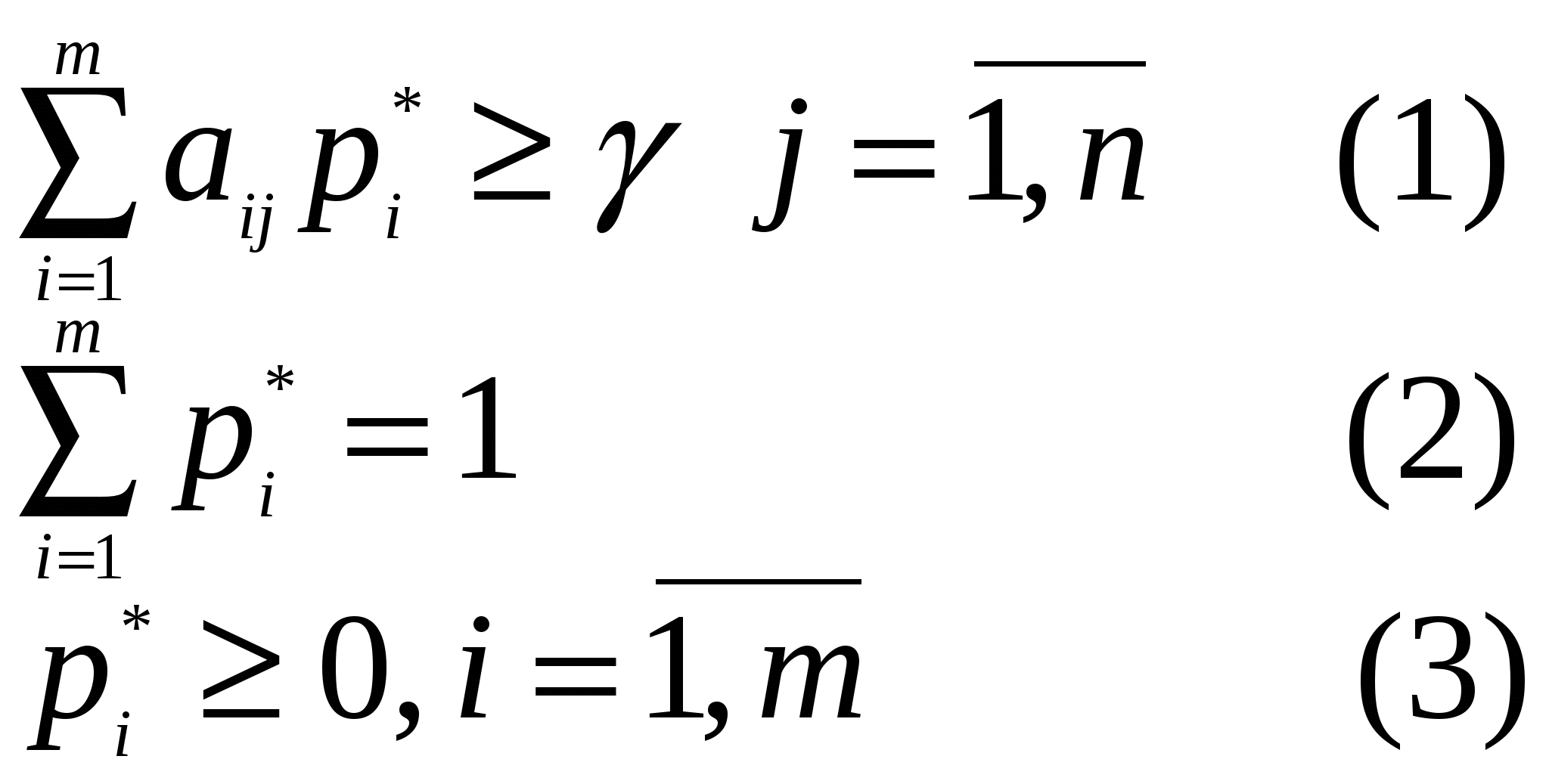 Цена игры Таким образом задача нахождения решения игры свелась к задаче линейного программирования (1)-(4), в которой необходимо найти вероятности Преобразуем эту ЗЛП к более удобному виду. Для этого предположим, что Теперь, поделив левую и правую части каждого из неравенств (1)-(3) на величину  Таким образом определение оптимальной смешанной стратегии Определим оптимальную смешанную стратегию Пусть игрок игрок Так как игрок 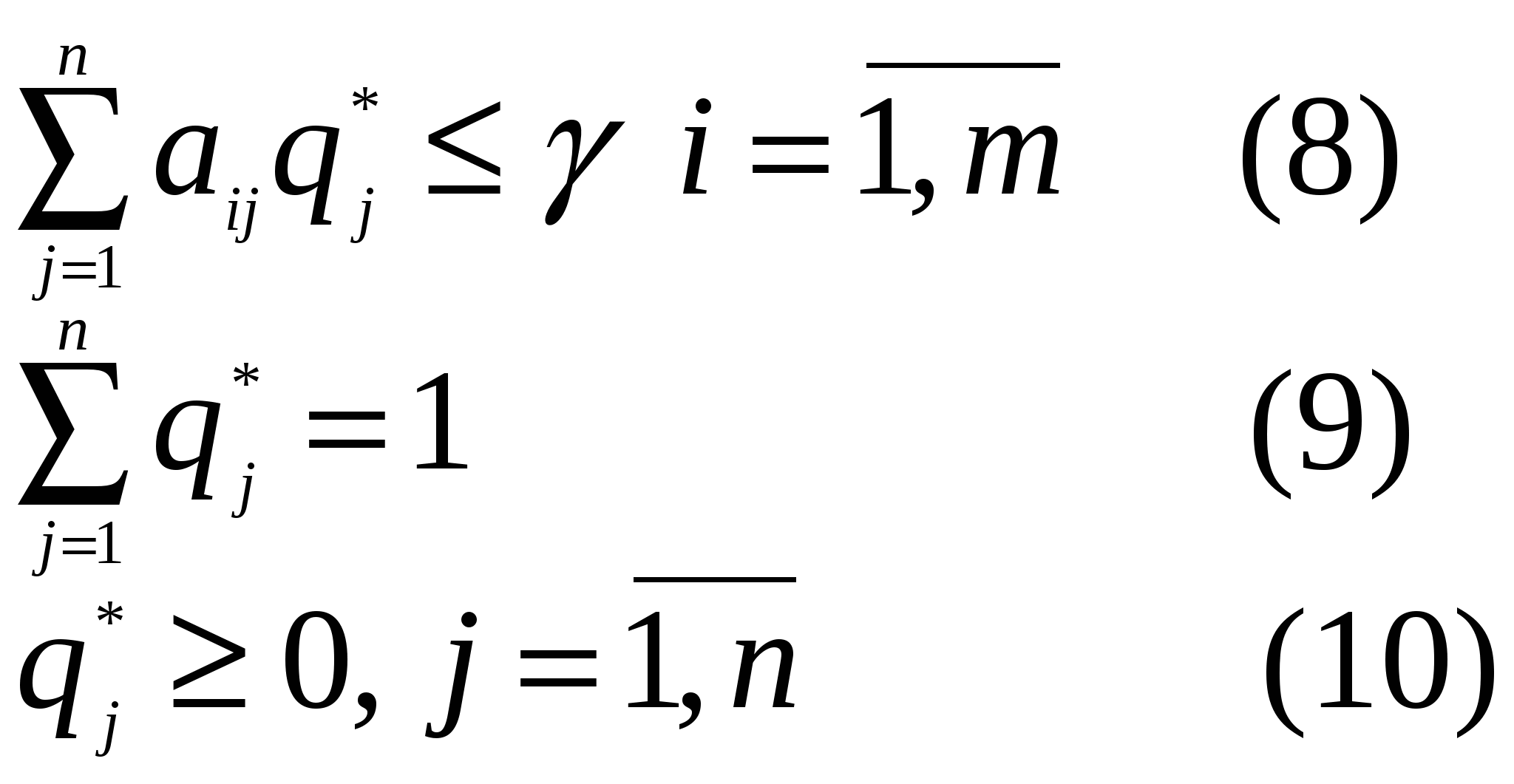 Игрок Теперь преобразуем ЗЛП (8)-(11). Для этого разделим левые и правые части выражений (8)-(10) на величину 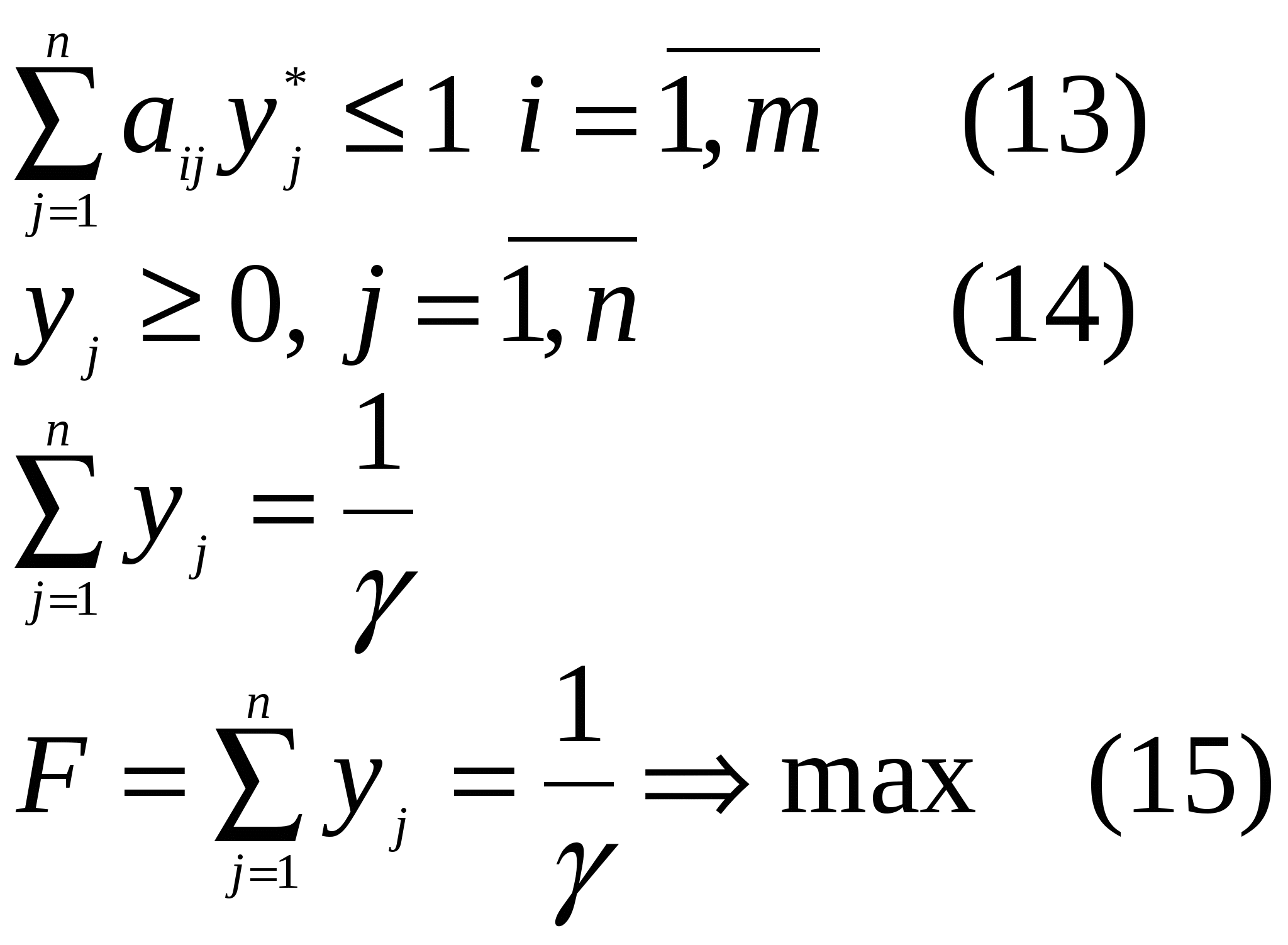 Пусть Таким образом найденная пара оптимальных стратегий ( Цена игры Покажем, что ЗЛП (13)-(15) имеет решение. Для этого необходимо, чтобы условия (13)-(14) были совместны, то есть имели хотя бы одно решение, а максимизируемая целевая функция была ограничена сверху. Действительно, ограничения (13)-(14) совместны, так как Теорема. Любая парная конечная игра с нулевой суммой имеет решение по крайне мере среди смешанных стратегий. |
