Лекция 19. Формула Тейлора. Ряд Тейлора.
19.1. Формула Тейлора1.
Рассмотрим произвольный многочлен степени n:
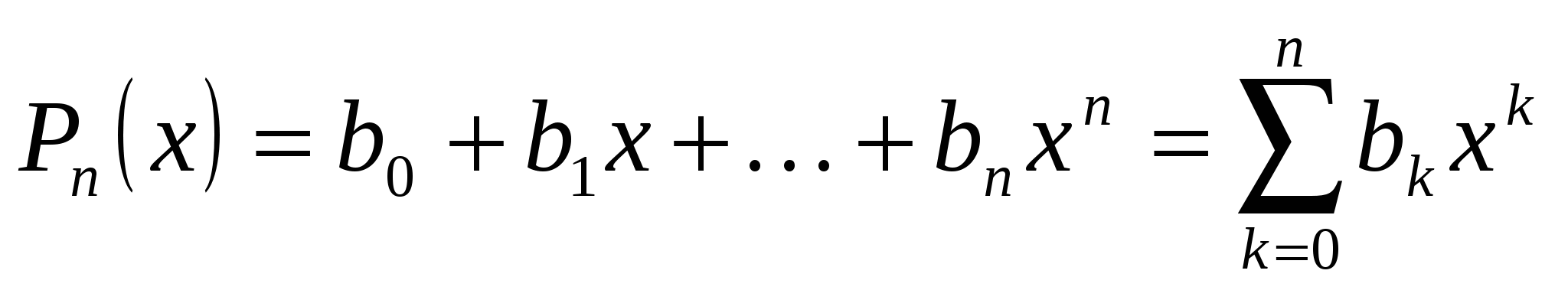 . .
Пусть 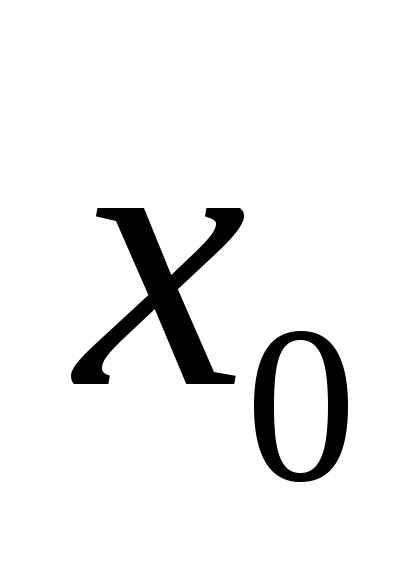 – любое фиксированное число. Полагая – любое фиксированное число. Полагая 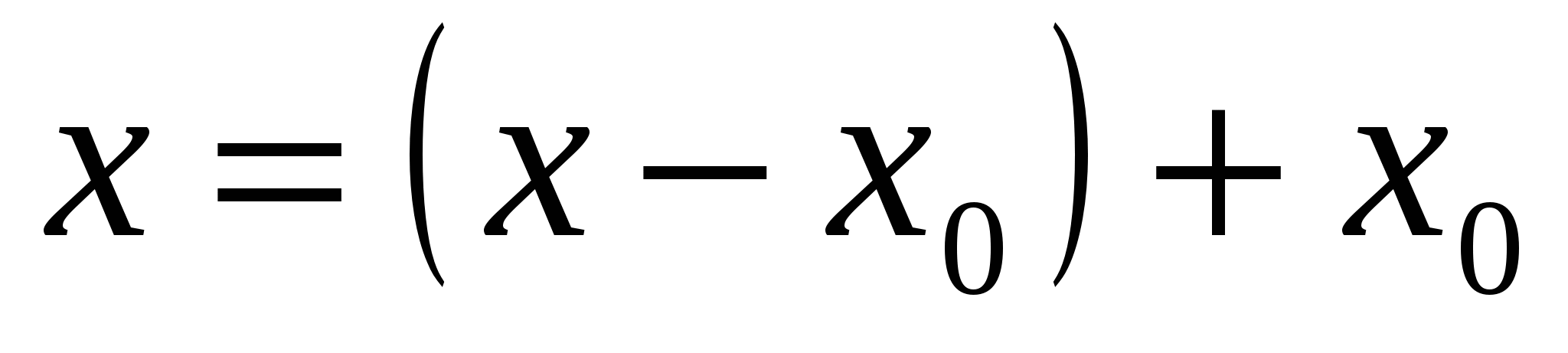 , получим: , получим:
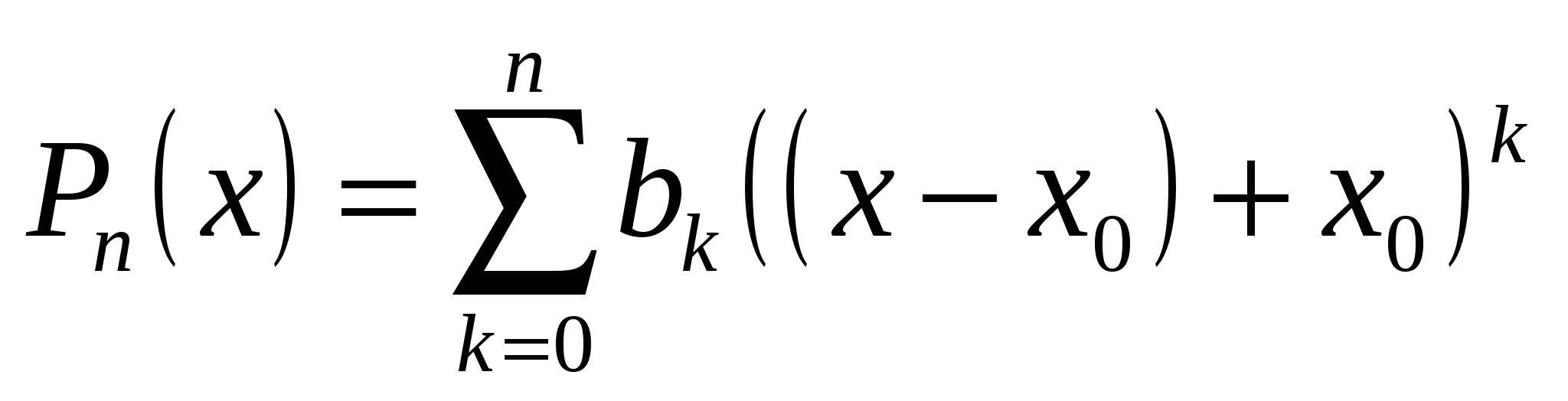 . (19.1) . (19.1)
Запишем также в виде
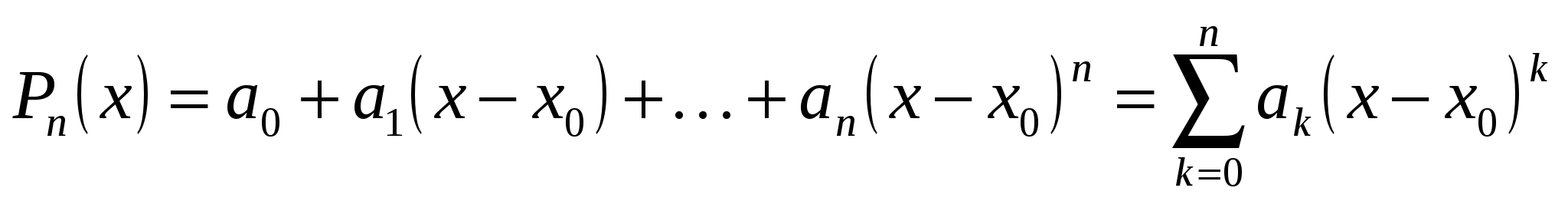 , (19.2) , (19.2)
где 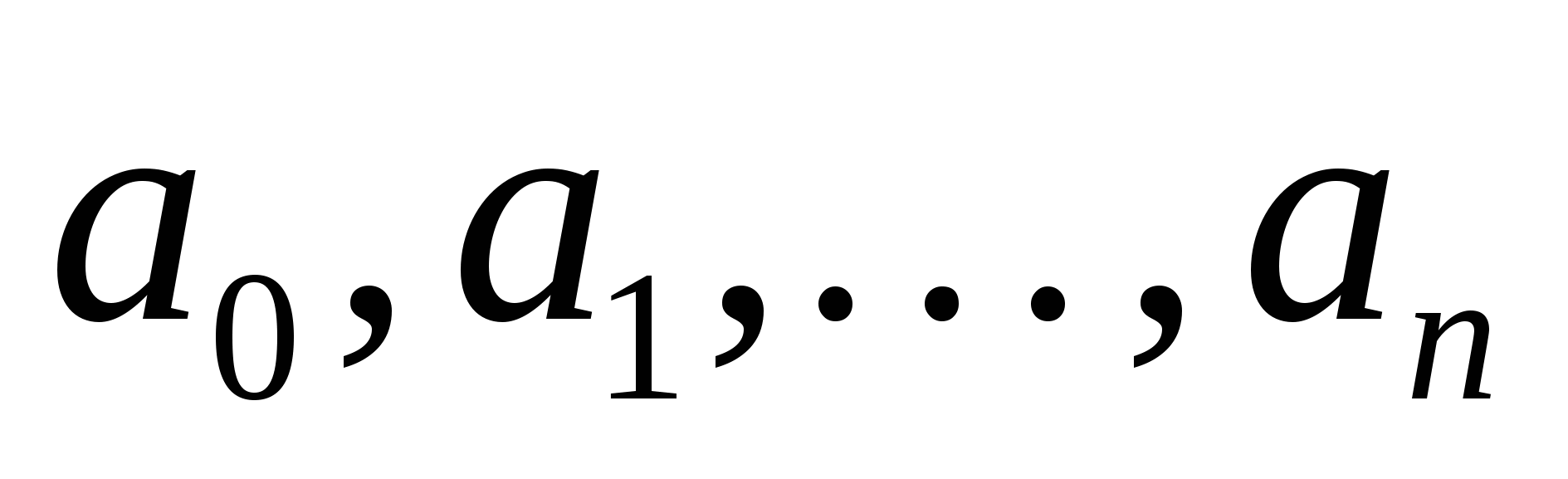 – числа, зависящие от – числа, зависящие от 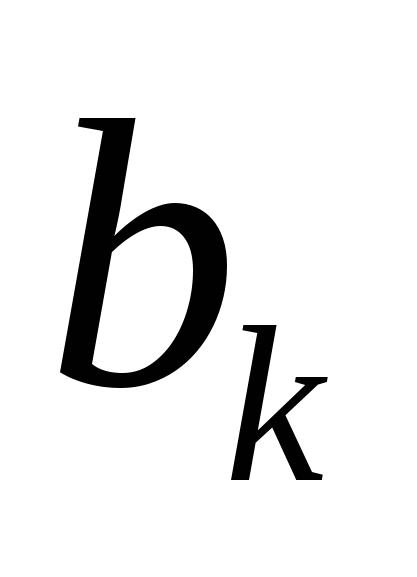 и и 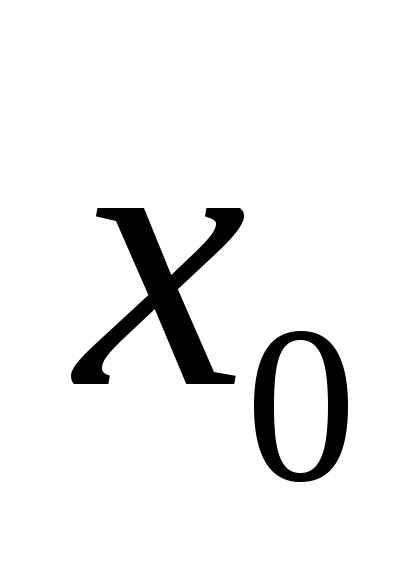 – коэффициенты разложения – коэффициенты разложения 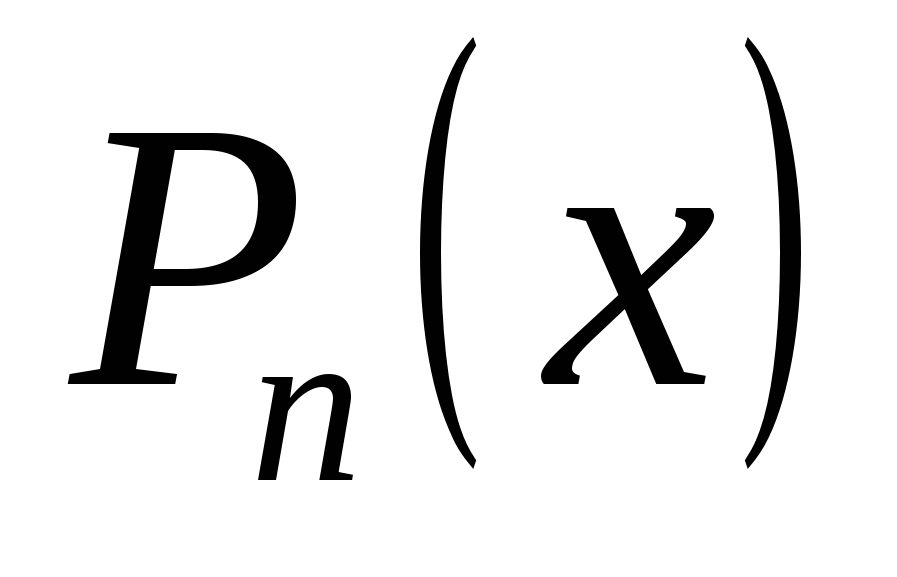 по степеням по степеням 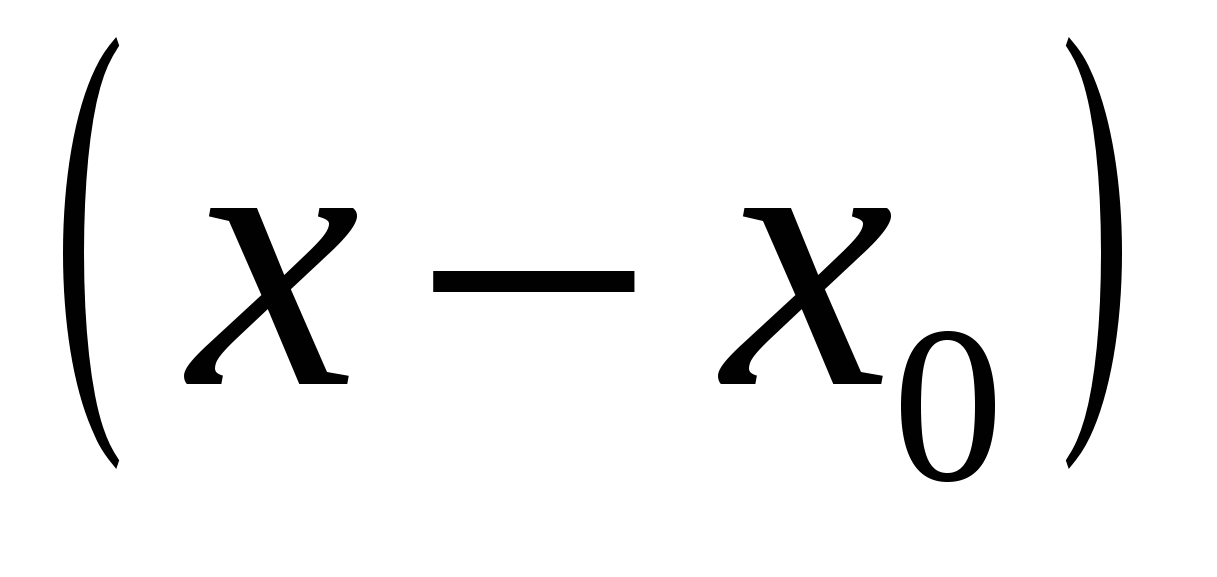 . Например, . Например, 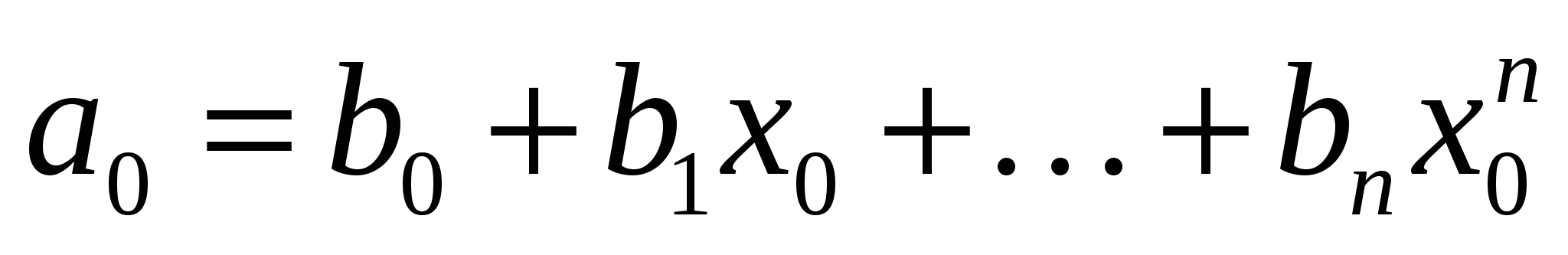 . .
Из (19.1) не видно, что 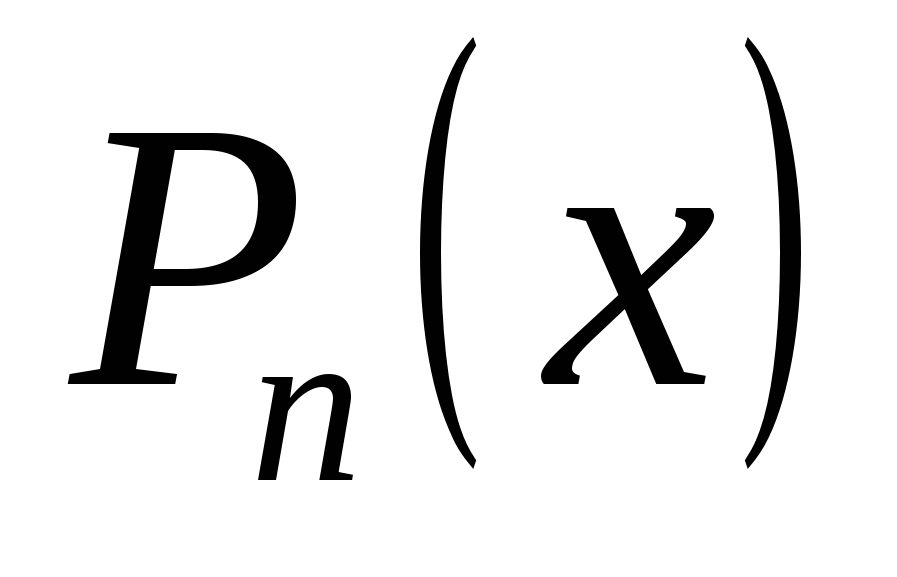 от от 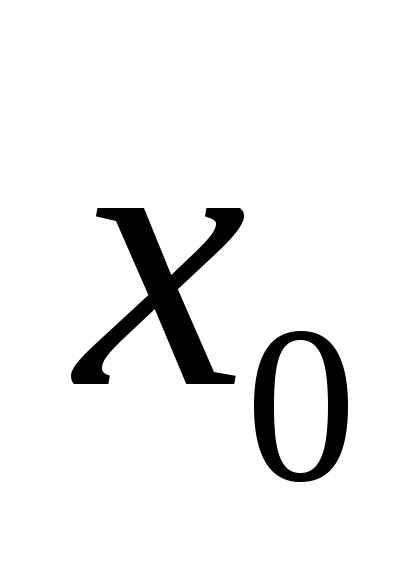 на самом деле не зависит. Найдём производные на самом деле не зависит. Найдём производные 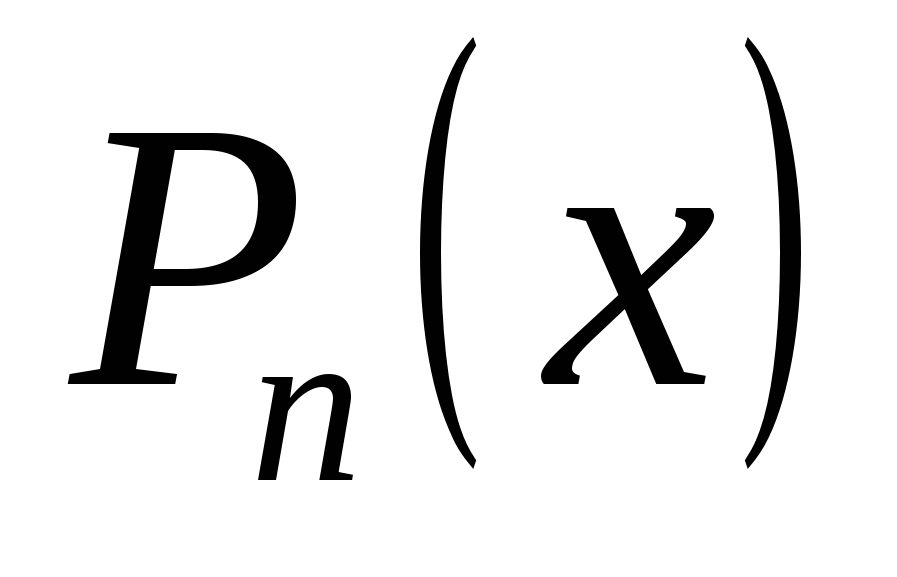 : :
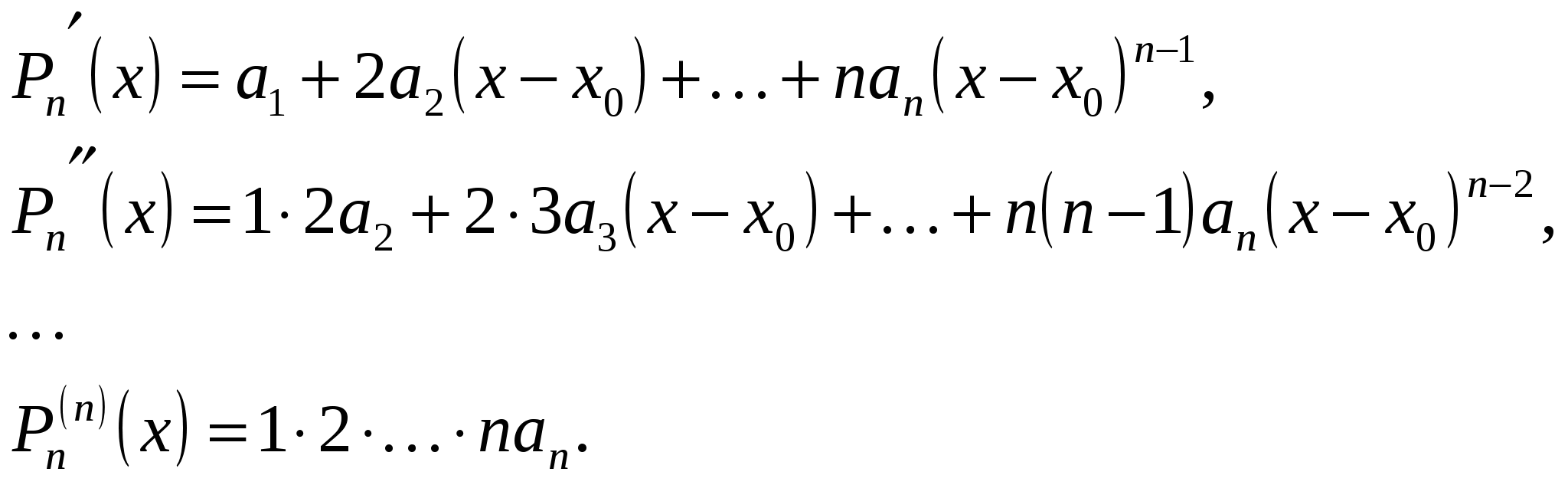 . (19.3) . (19.3)
Следующие производные равны нулю.
Полагая в формулах (19.2) и (19.3) 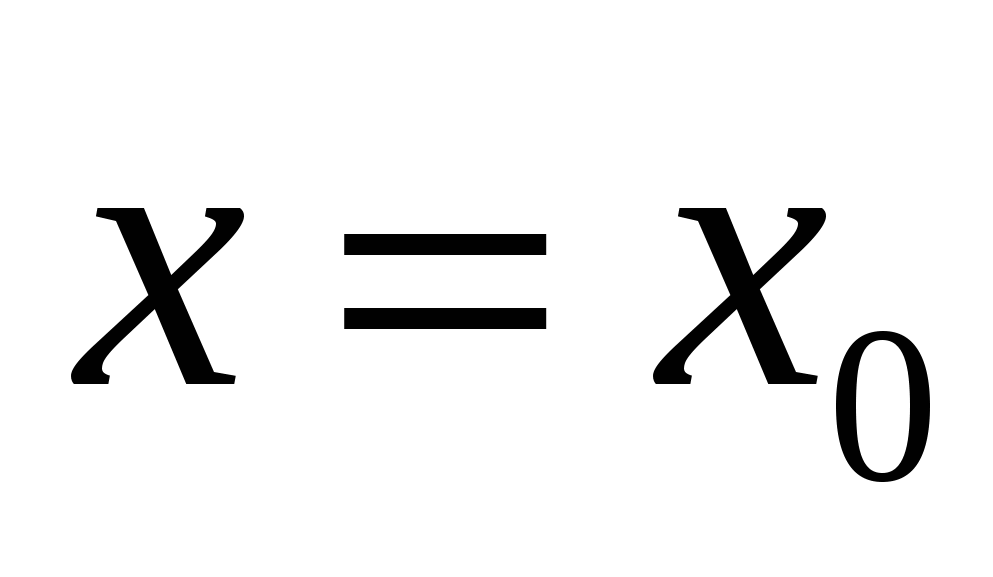 , получаем: , получаем:
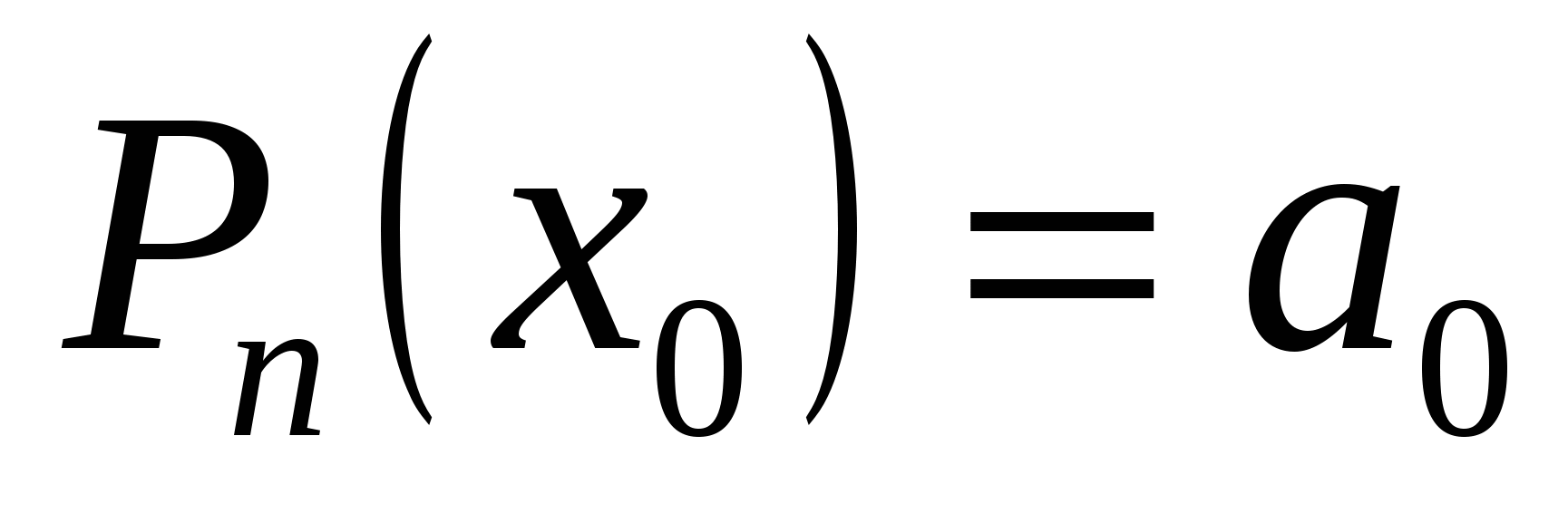 , , 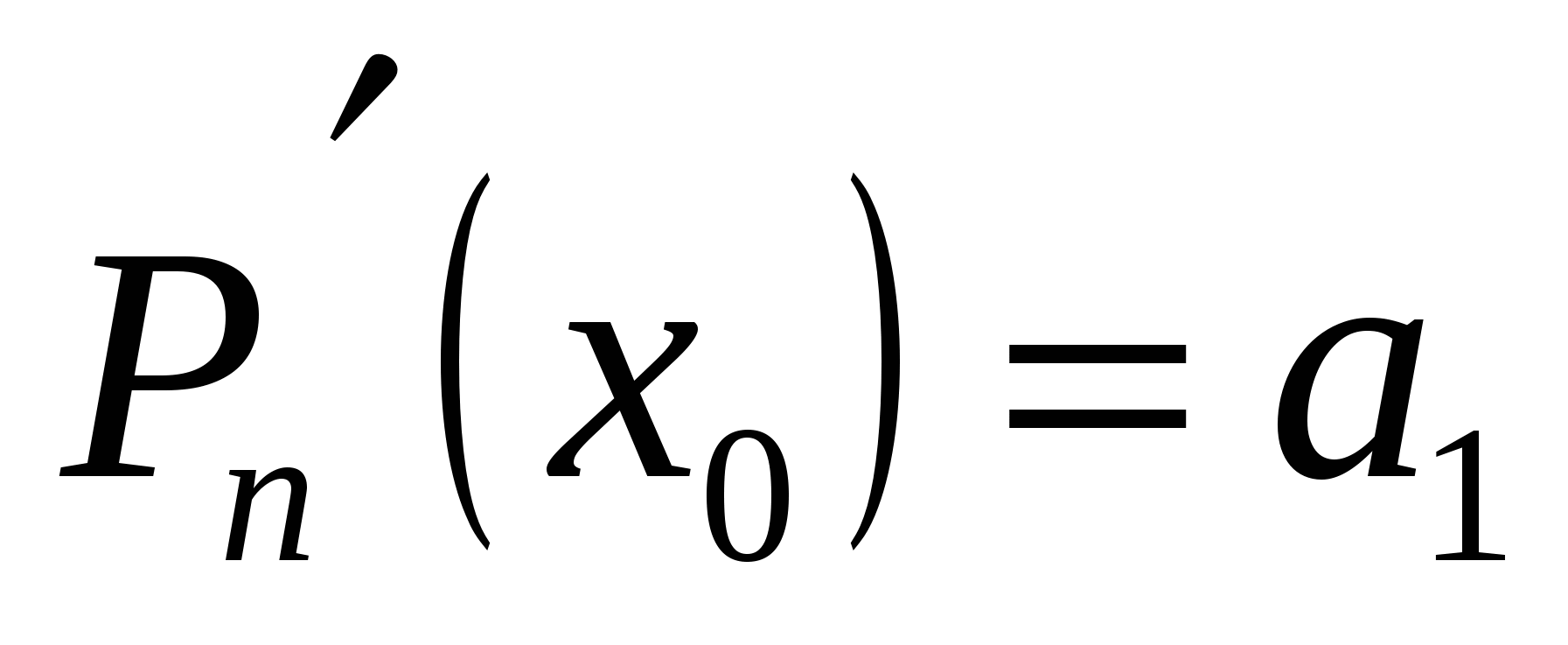 , , 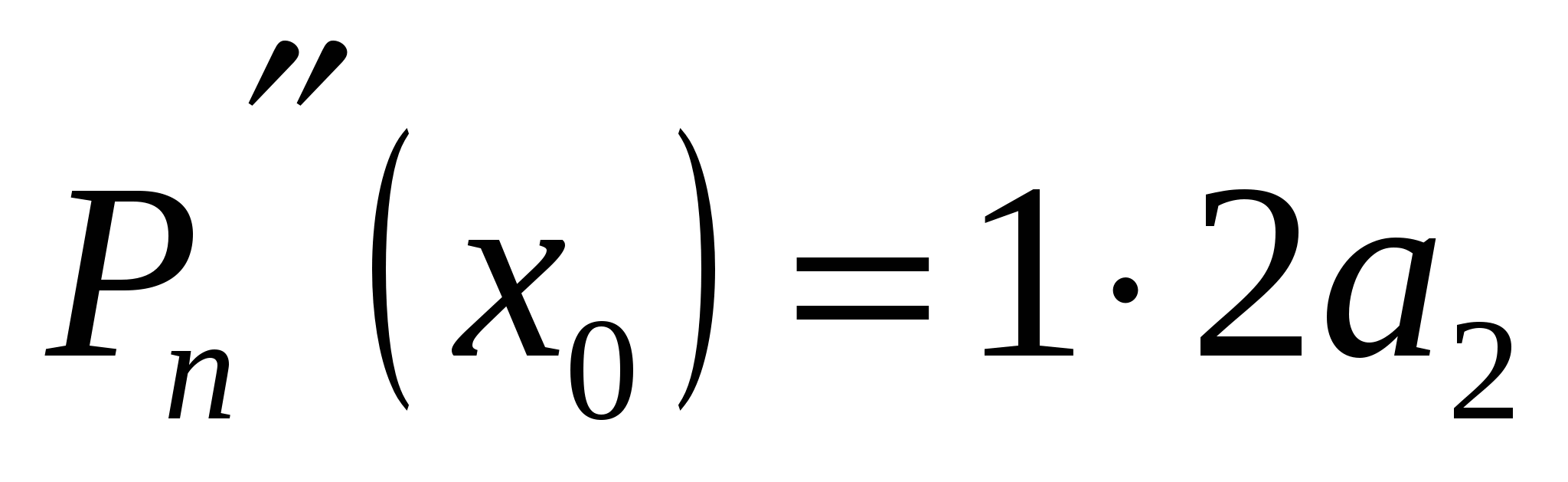 , ,  , , 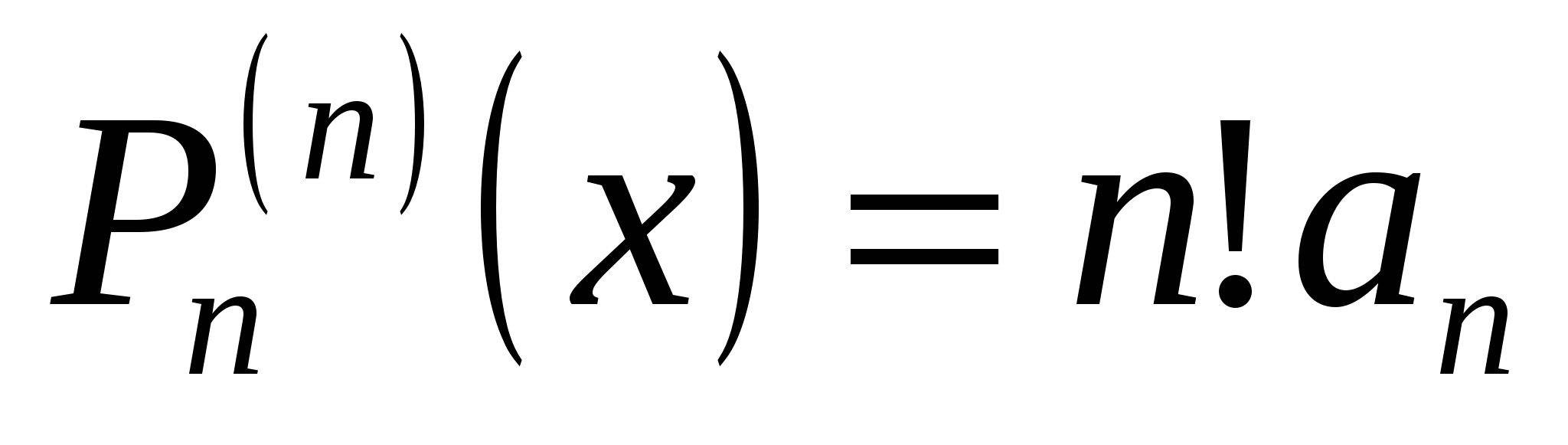 , ,
то есть
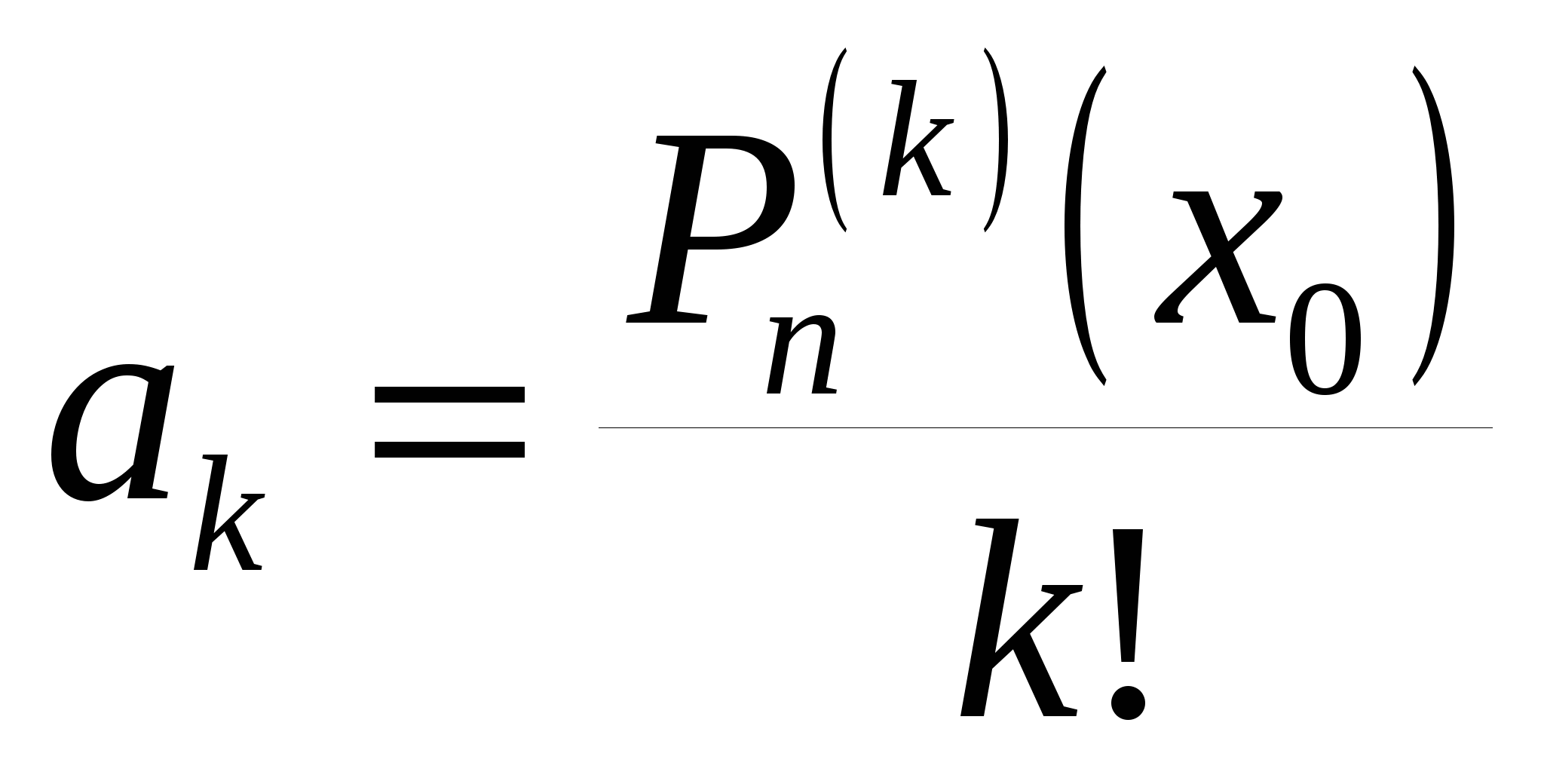 . (19.4) . (19.4)
Таким образом,
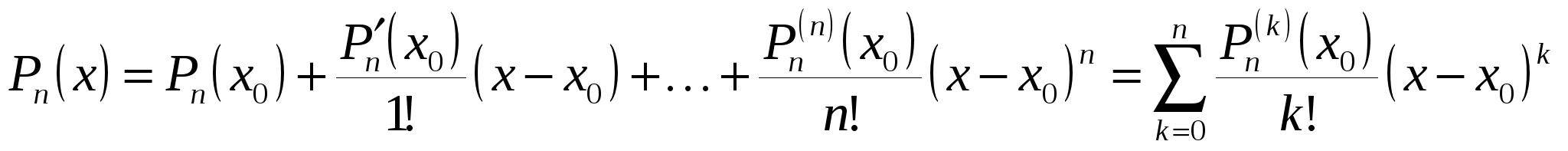 . (19.2*) . (19.2*)
Это формула Тейлора для многочлена 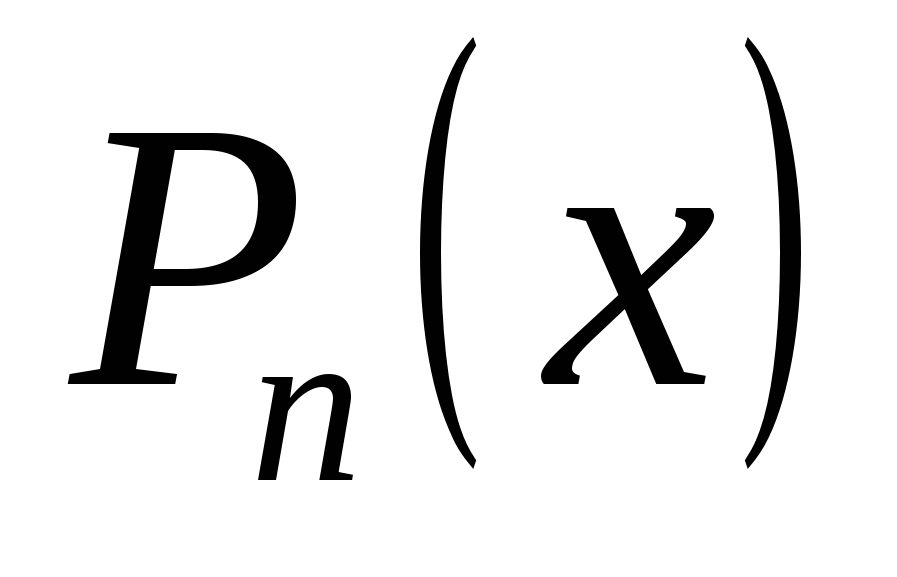 по степеням по степеням 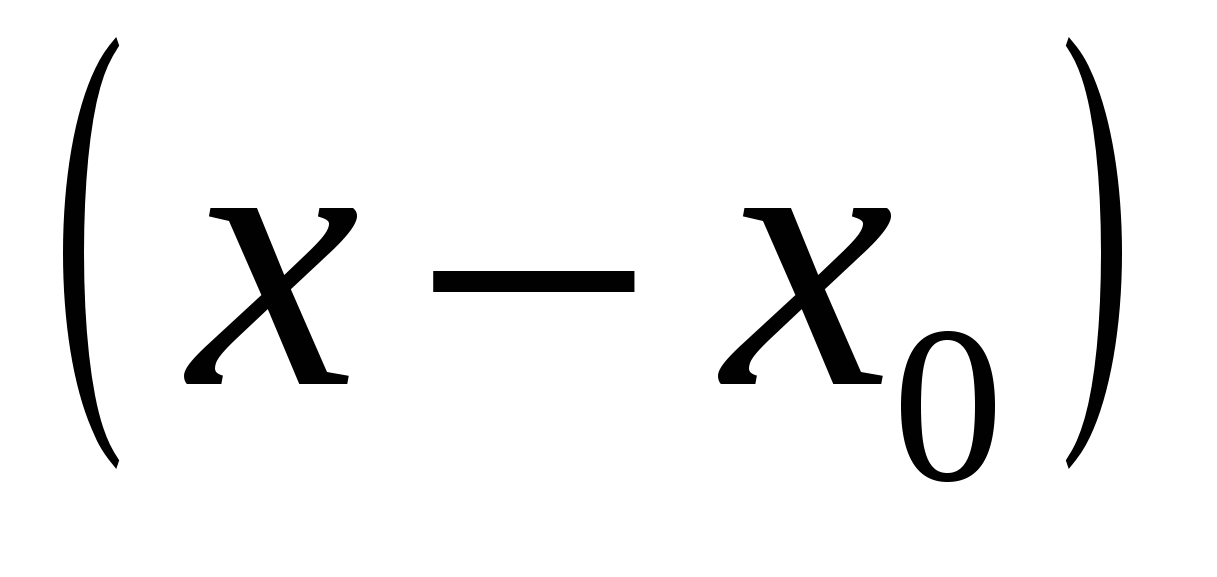 . .
Отметим, что правая часть (19.2*) фактически не зависит от 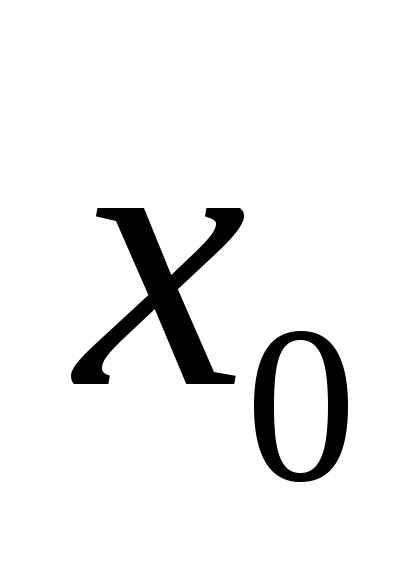 . .
Пример 19.1. Пусть 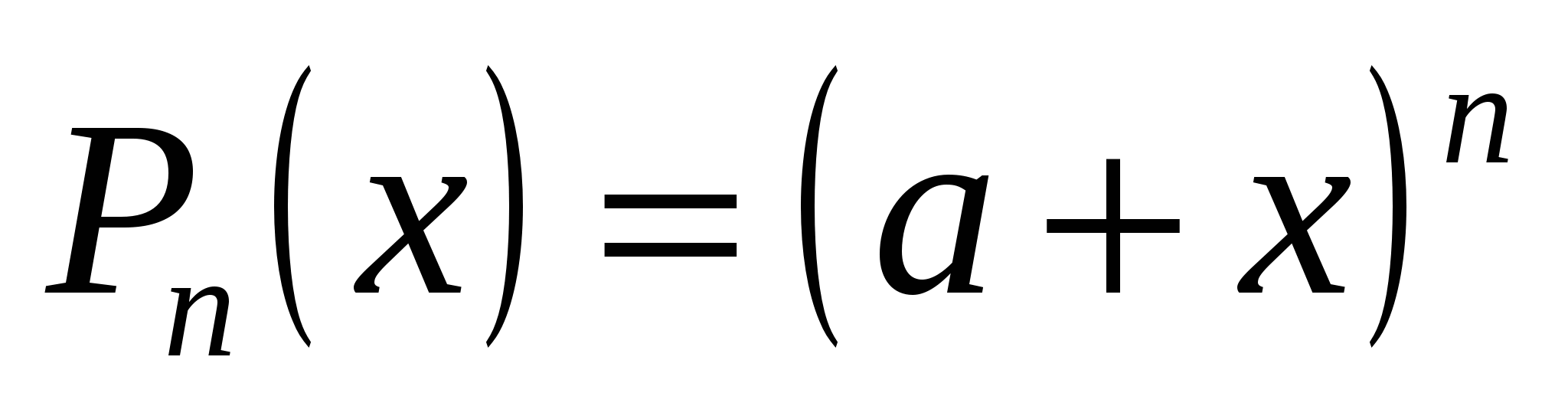 , , 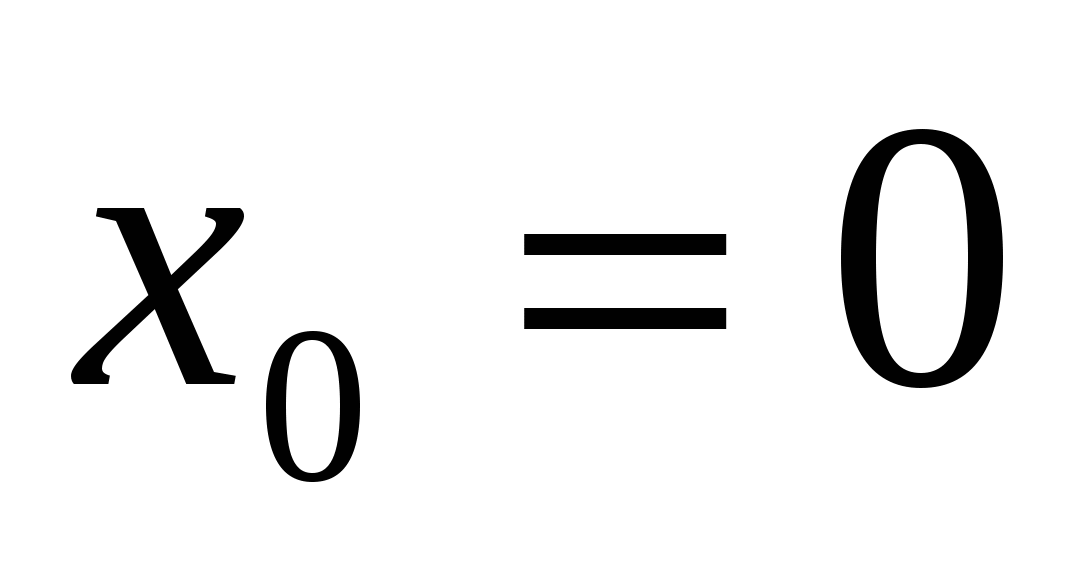 . .
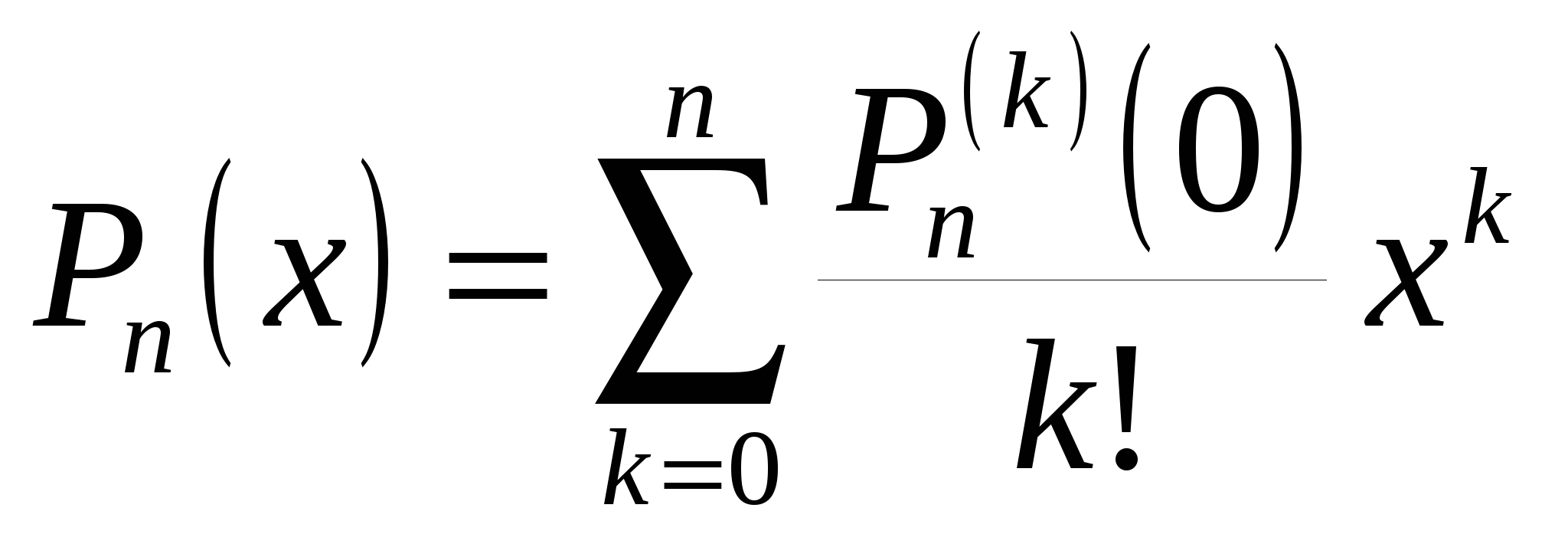 , ,
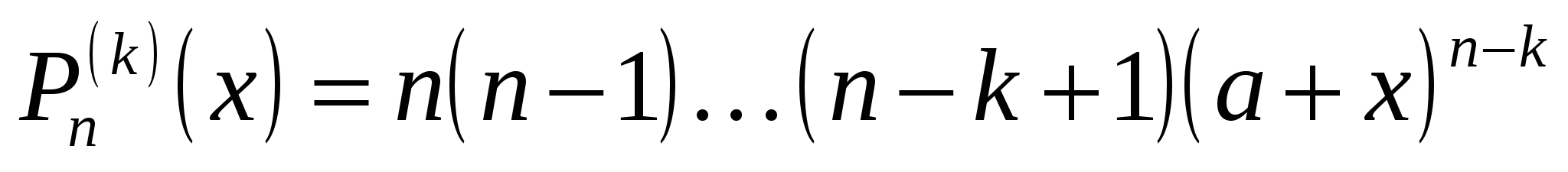 , , 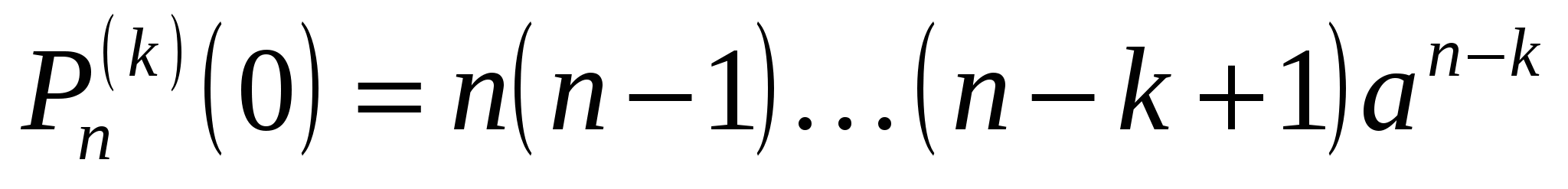 , ,
после чего получаем формулу бинома Ньютона
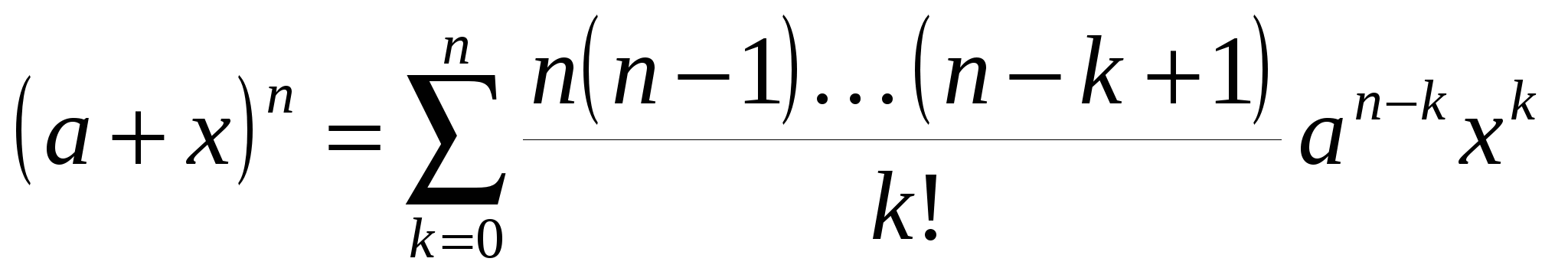 . .
19.2. Остаточный член формулы Тейлора.
Рассмотрим любую функцию 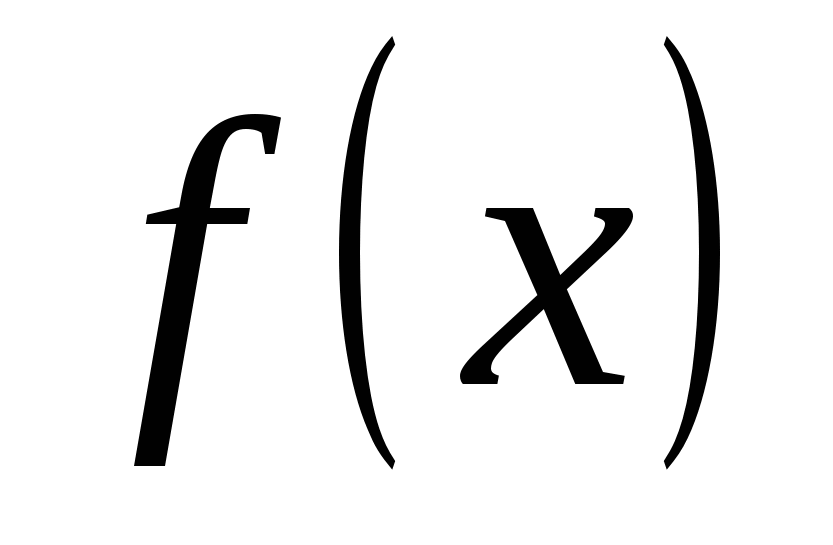 , которая имеет непрерывные производные до , которая имеет непрерывные производные до 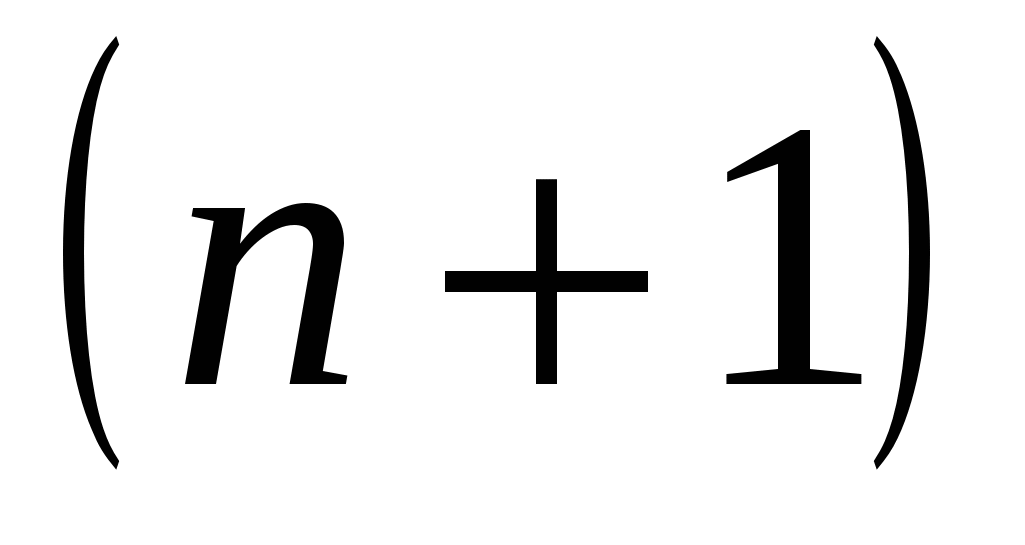 -го порядка в некоторой окрестности точки -го порядка в некоторой окрестности точки 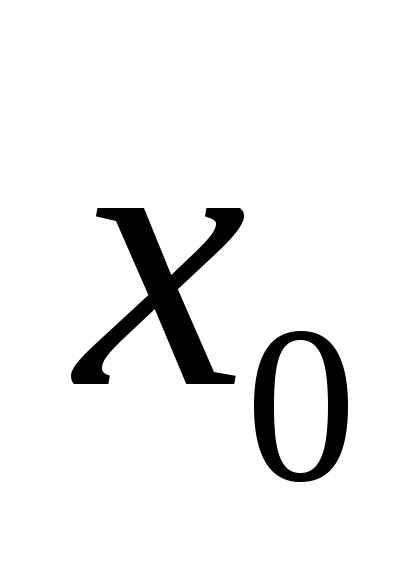 . Составим многочлен Тейлора n-й степени по степеням . Составим многочлен Тейлора n-й степени по степеням 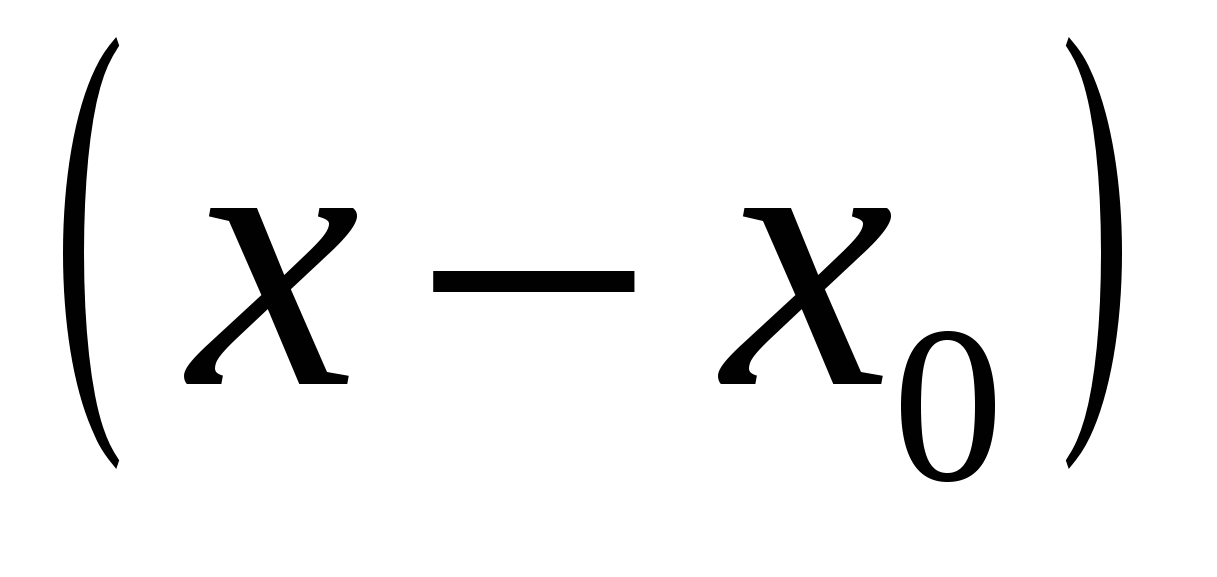 : :
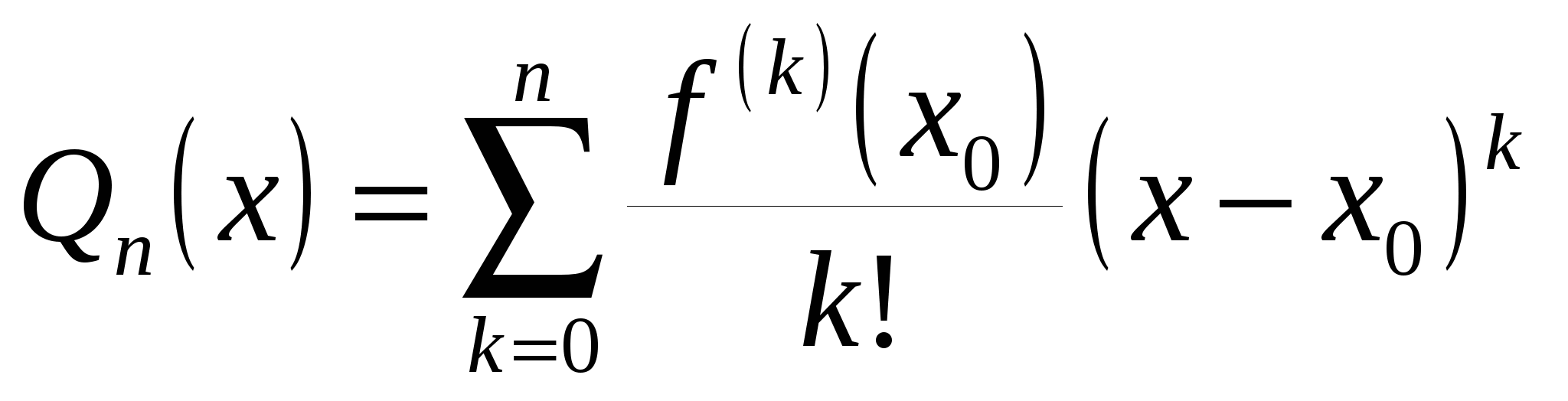 . (19.5) . (19.5)
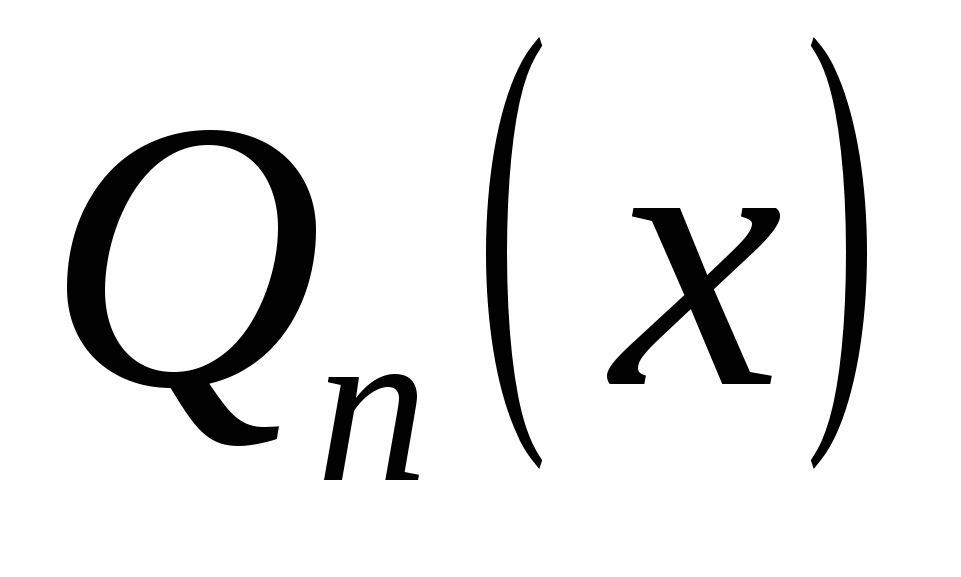 совпадает с функцией совпадает с функцией 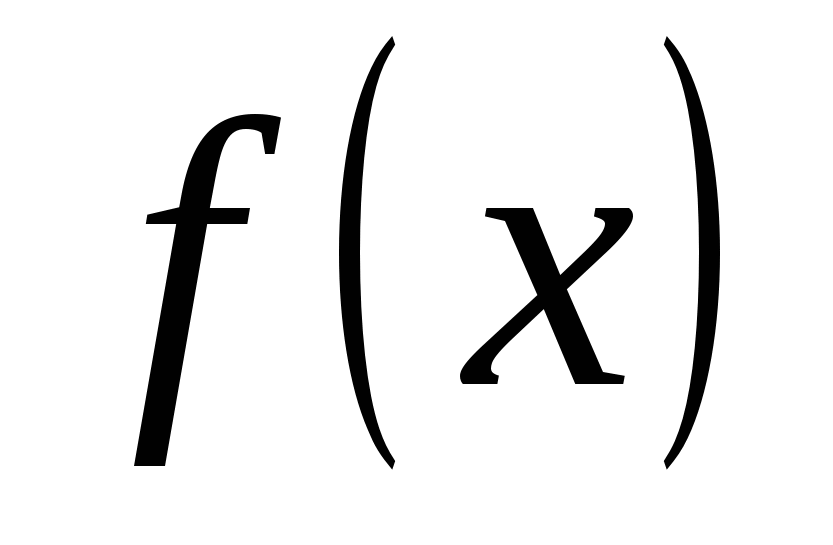 в точке в точке 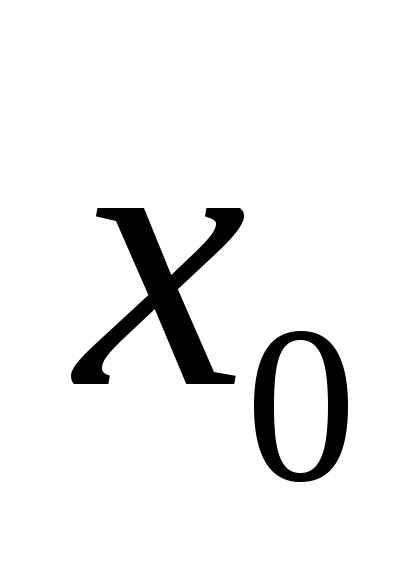 , но для всех x он не равен , но для всех x он не равен 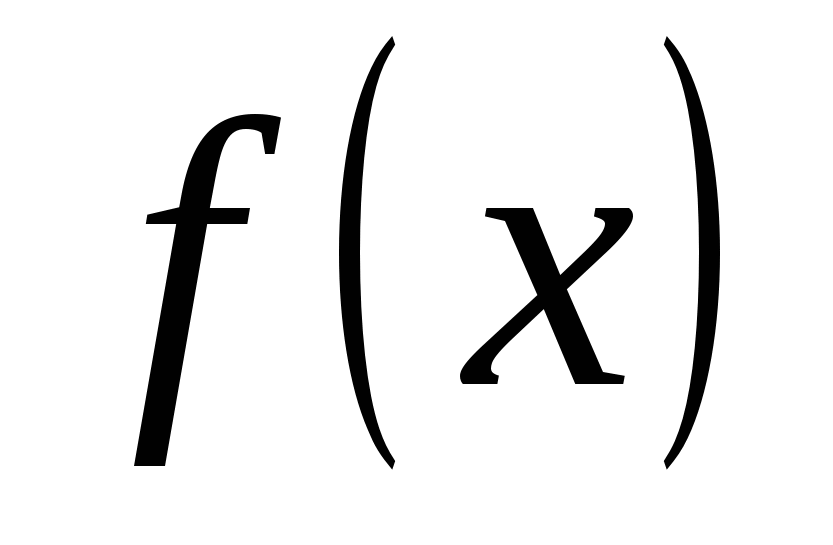 . Кроме того, . Кроме того,
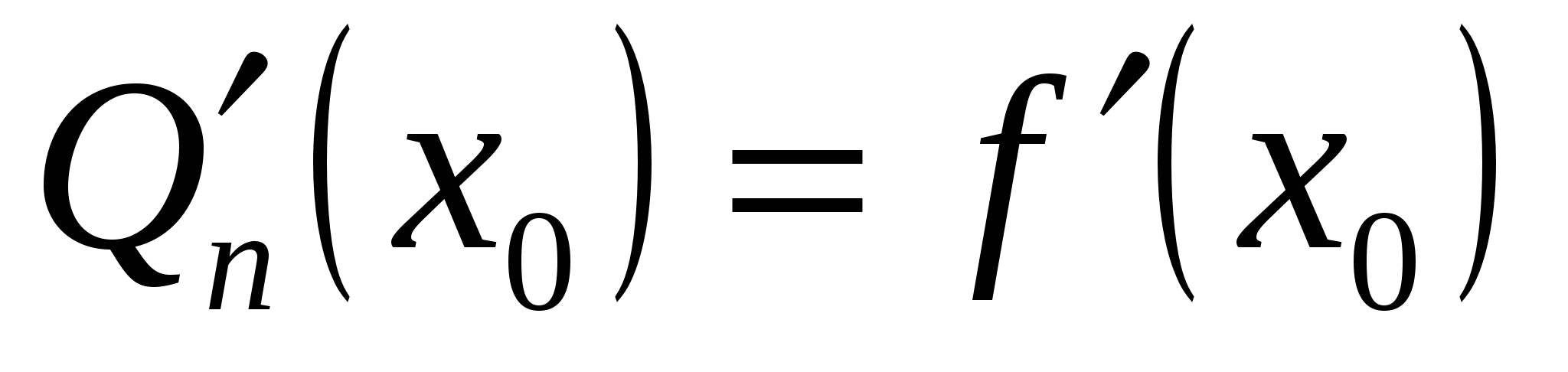 , ,  , , 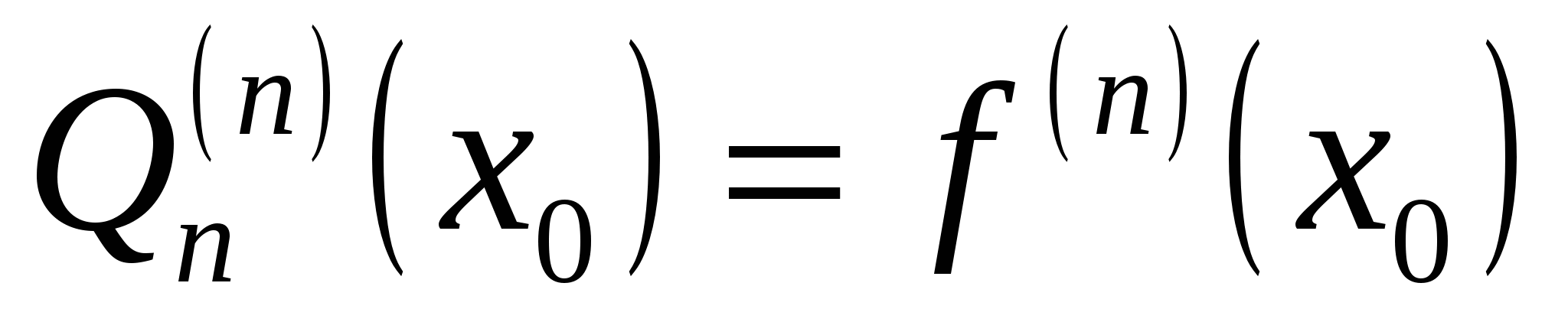 . .
Положим
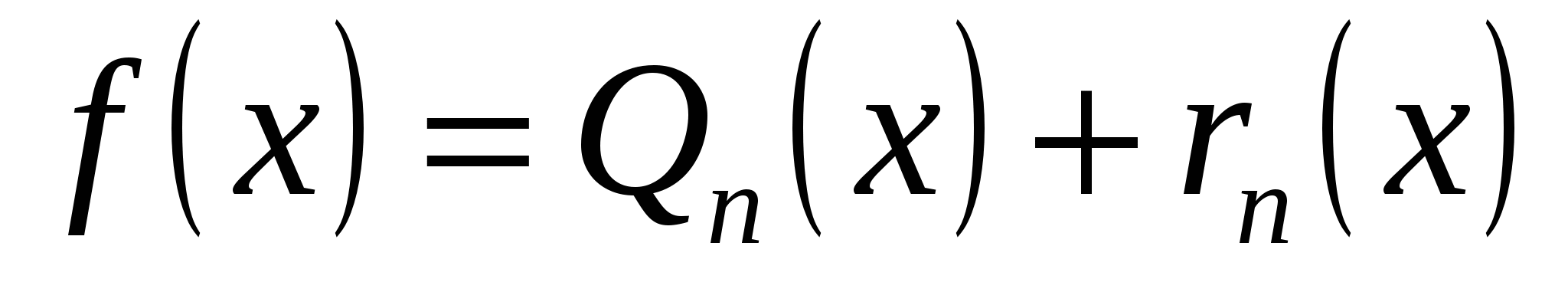 . (19.6) . (19.6)
Здесь 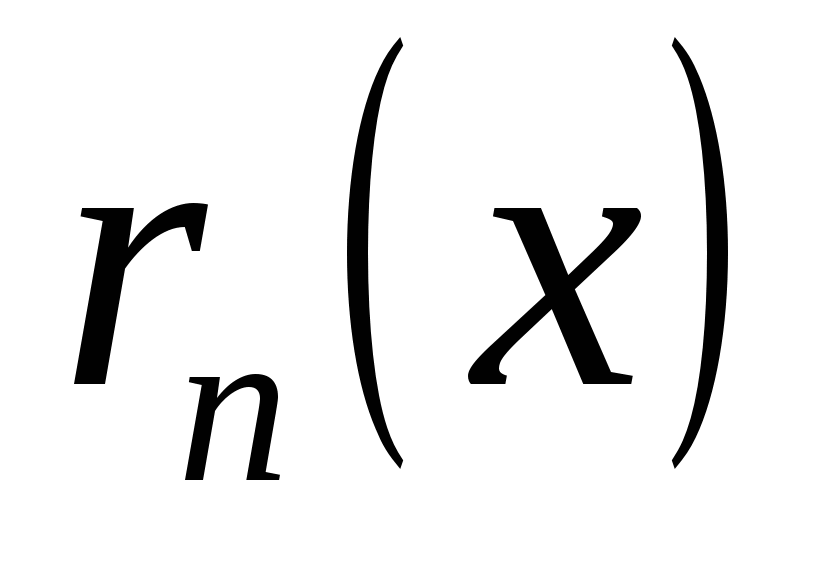 – остаточный член формулы Тейлора. Он показывает, какую погрешность мы допускаем при замене – остаточный член формулы Тейлора. Он показывает, какую погрешность мы допускаем при замене 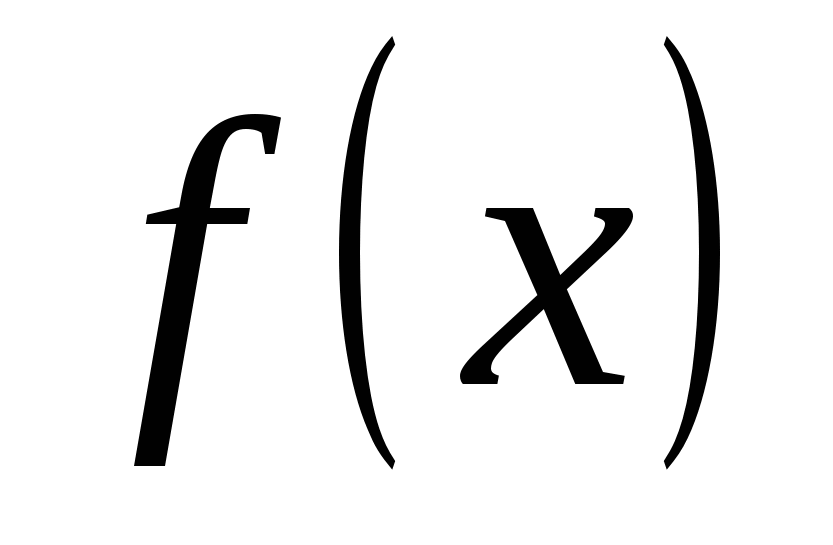 на многочлен Тейлора (19.5). на многочлен Тейлора (19.5).
Если функция 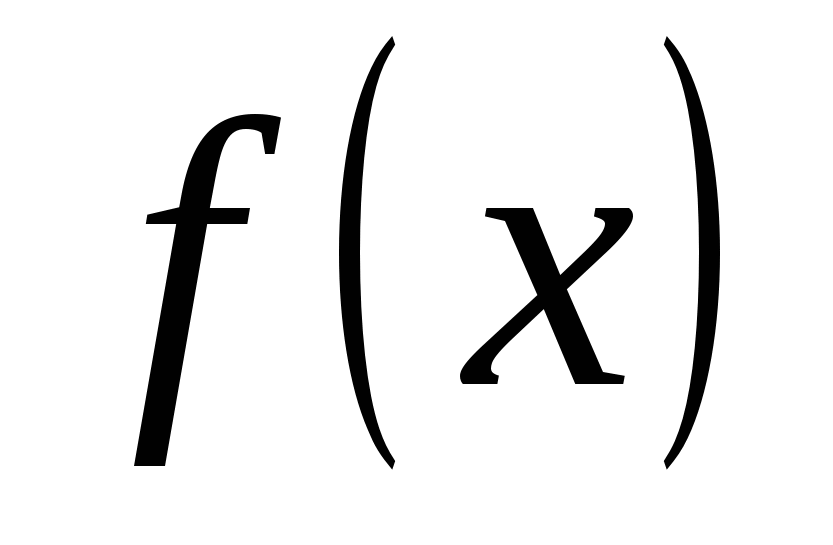 имеет в окрестности точки имеет в окрестности точки 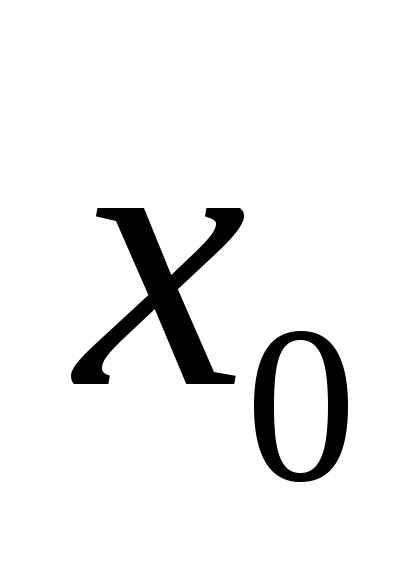 непрерывную производную непрерывную производную 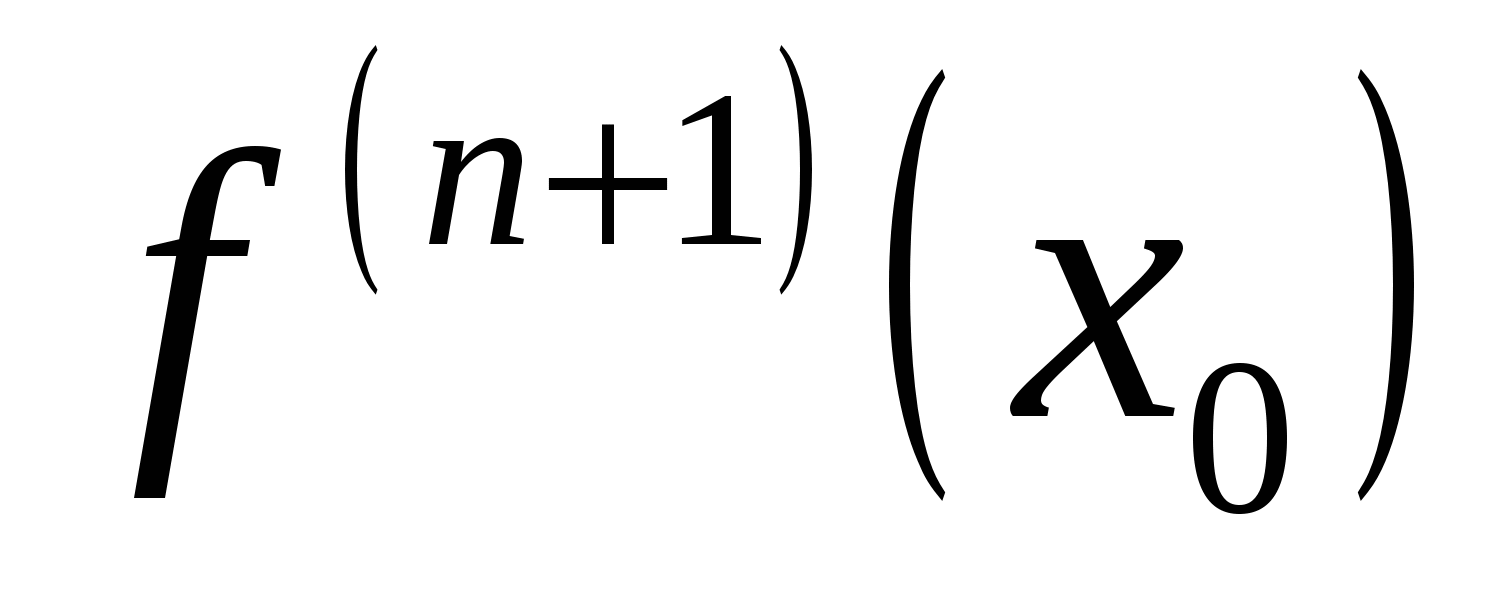 , то для , то для 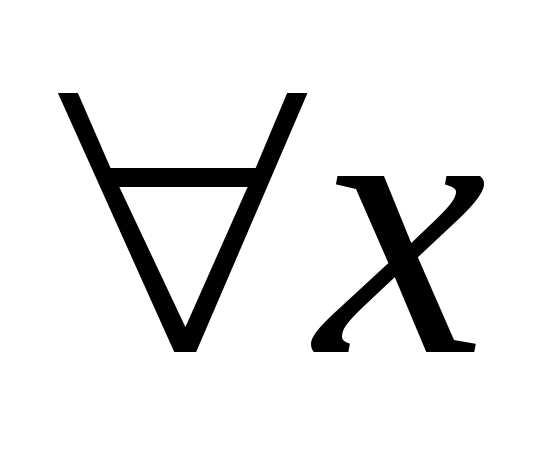 из этой окрестности найдётся точка из этой окрестности найдётся точка 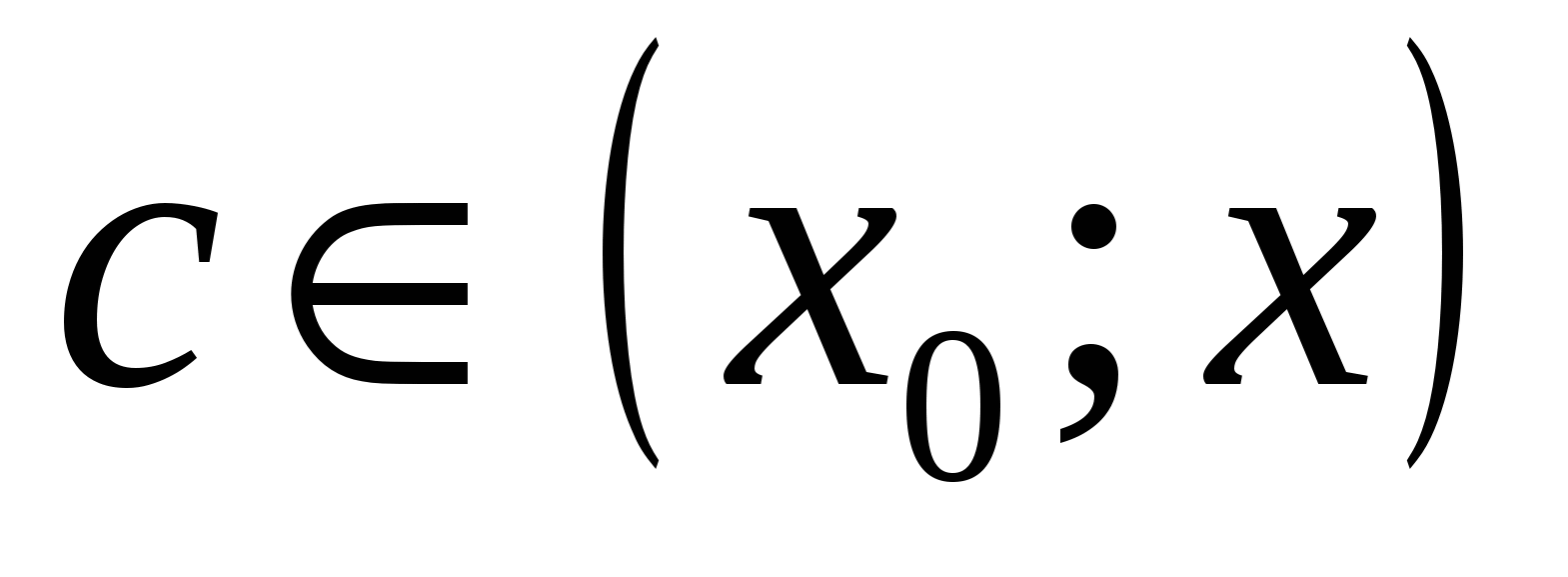 такая, что такая, что

(остаточный член в форме Лагранжа).
Функцию 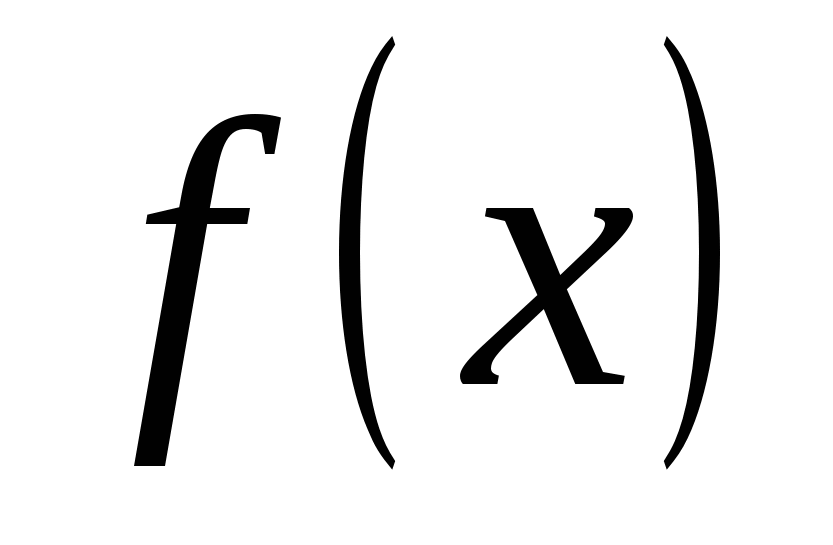 можно записать в виде: можно записать в виде:
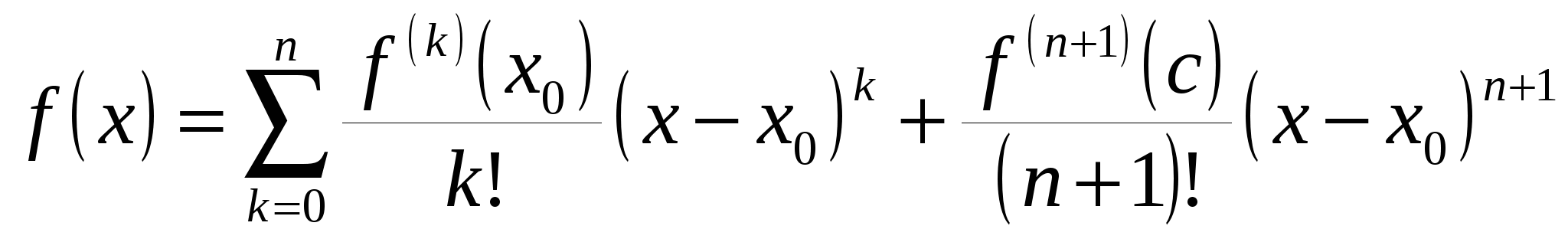 . (19.6*) . (19.6*)
Если 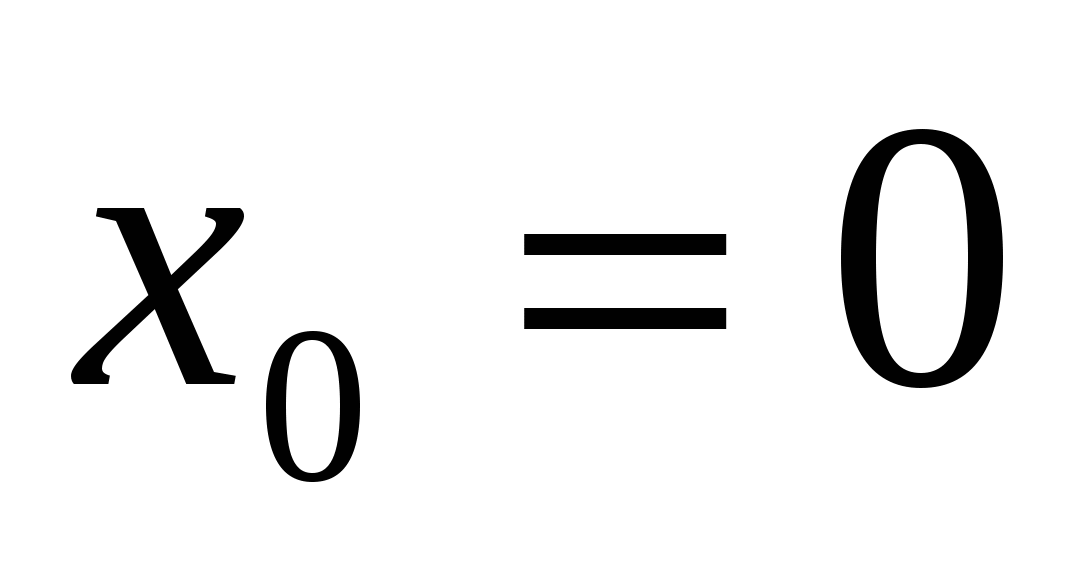 , то формулу (19.6*) называют формулой Маклорена1. , то формулу (19.6*) называют формулой Маклорена1.
Известны и другие формы остаточного члена формулы Тейлора.
Остаточный член в форме Коши: 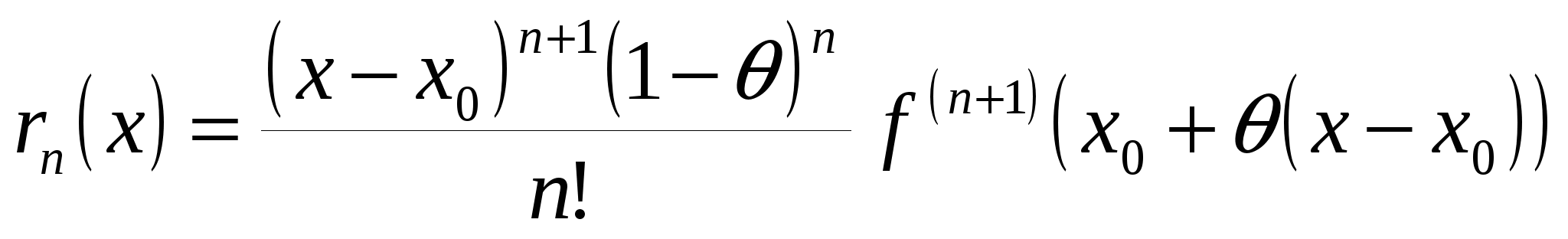 , где , где 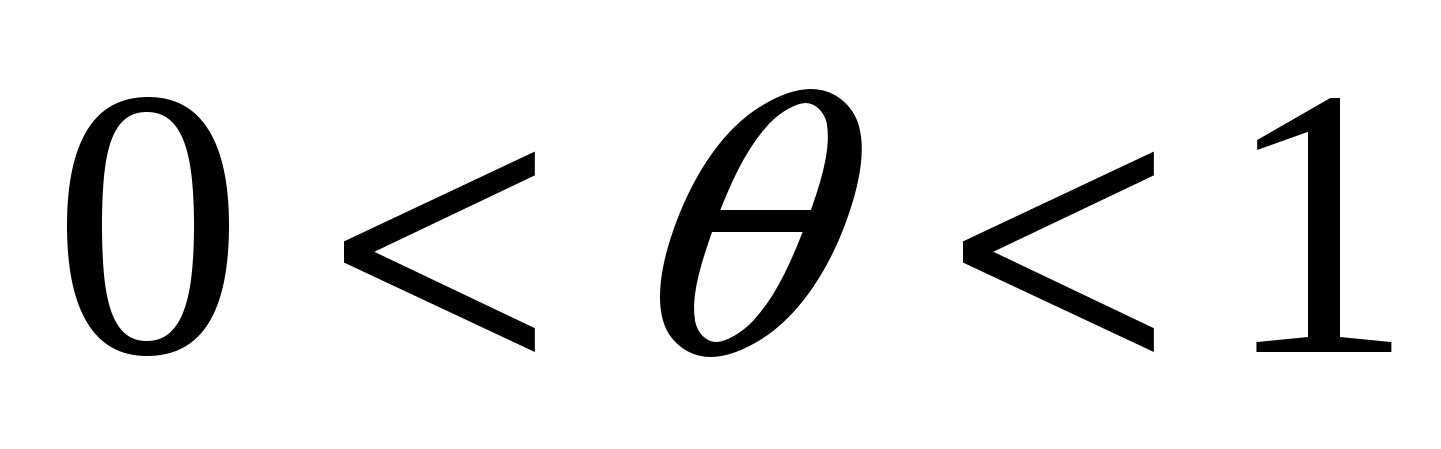 . .
Формула Тейлора с остаточным членом в смысле Пеано2:
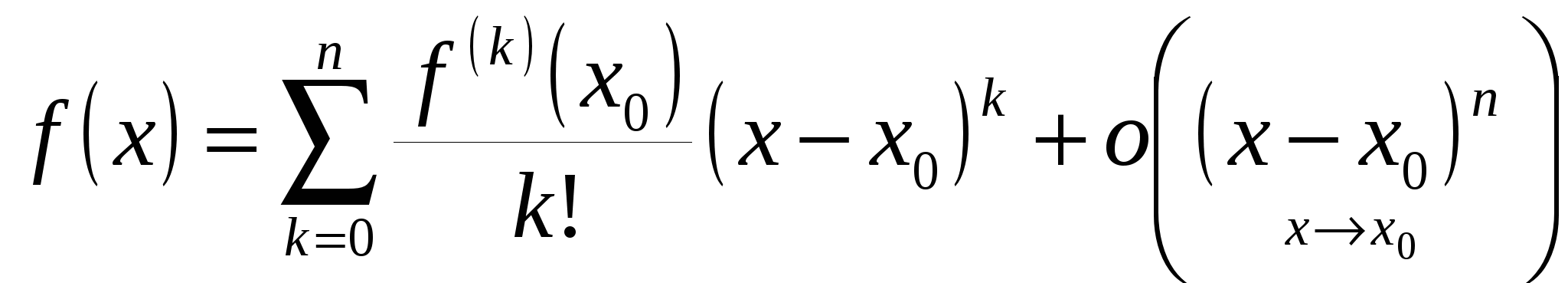 . .
Эта формула приспособлена для изучения функции 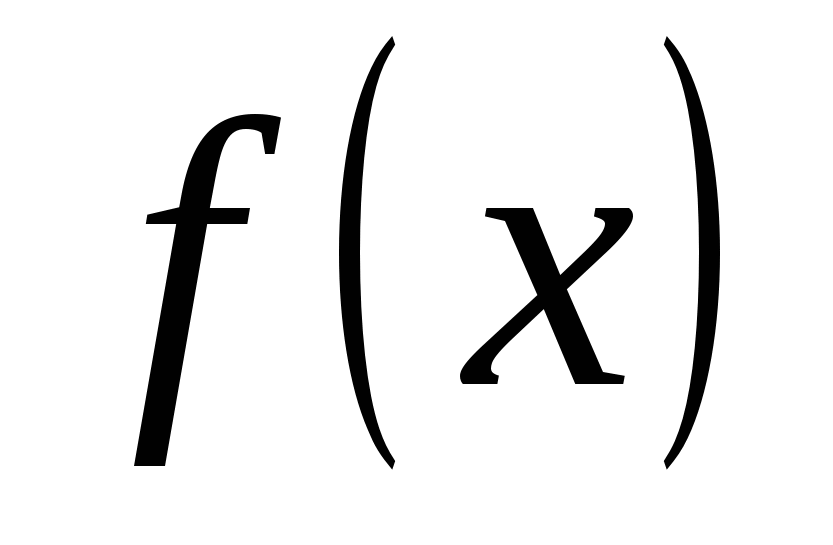 в окрестности точки в окрестности точки 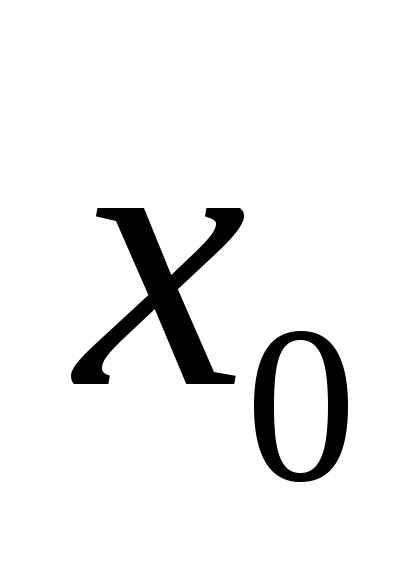 . .
19.3. Ряд Тейлора.
Определение 19.1. Выражение вида
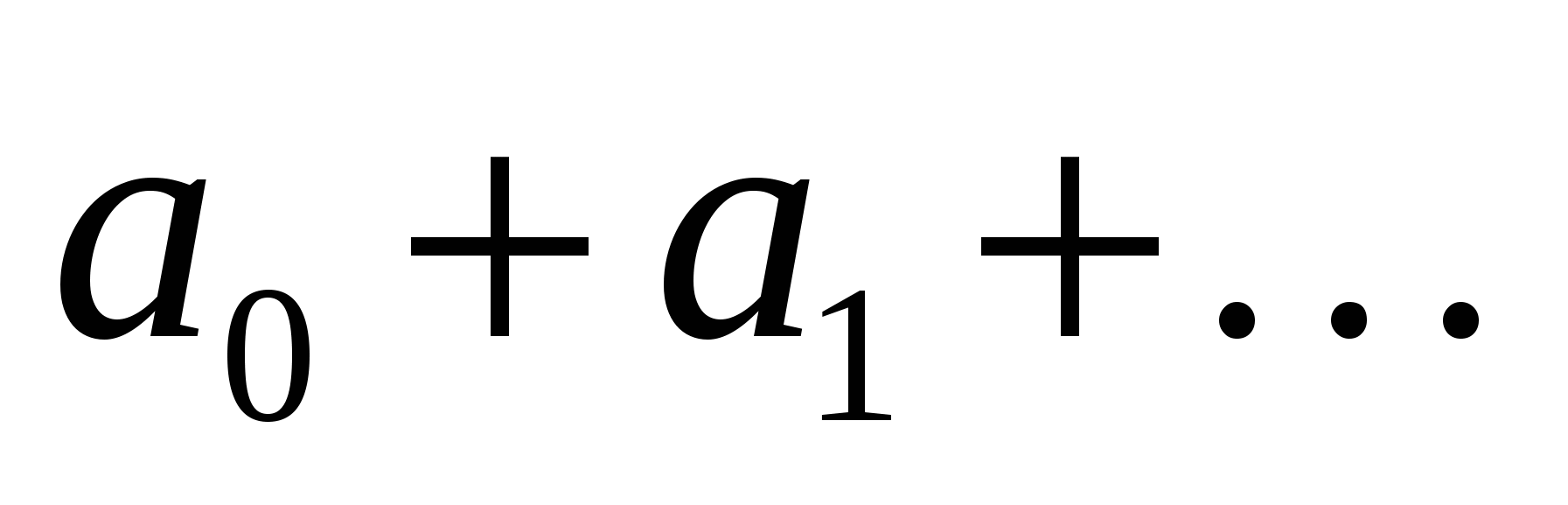 , (19.7) , (19.7)
или
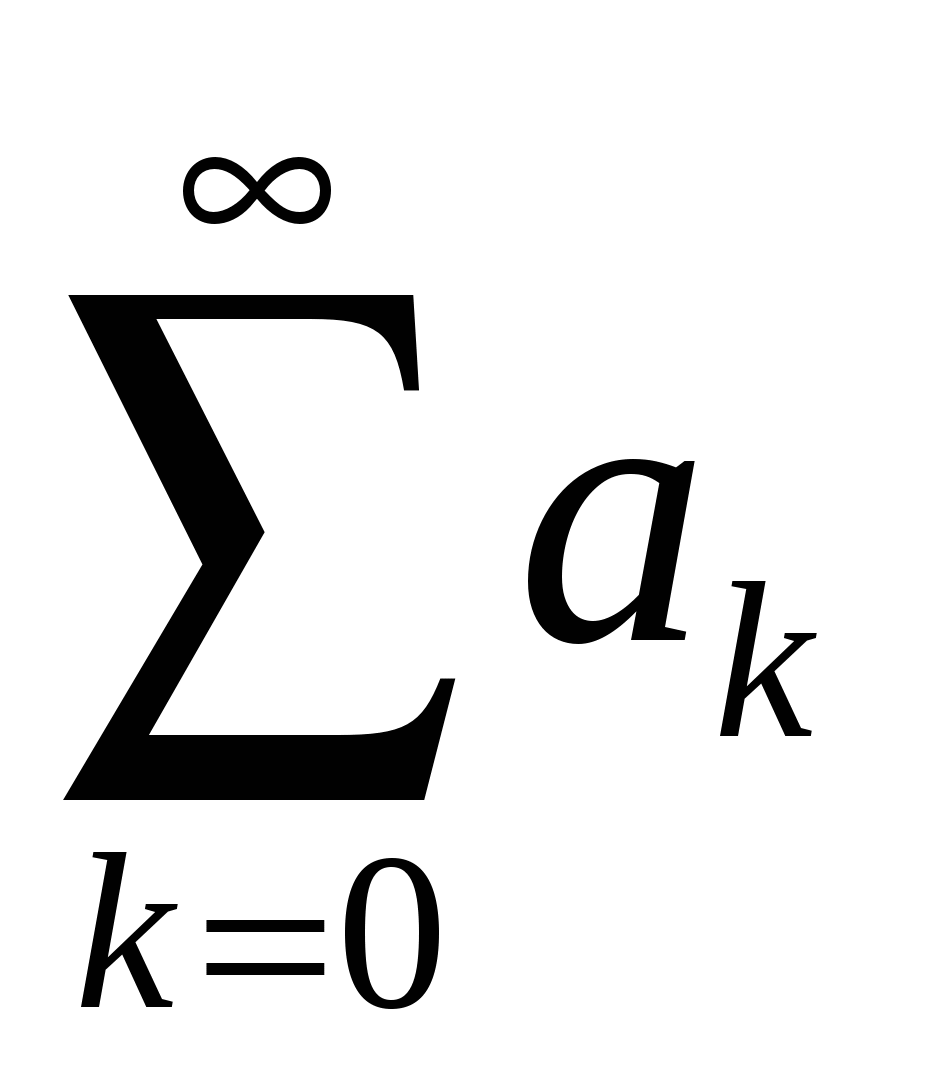 , (19.7*) , (19.7*)
где 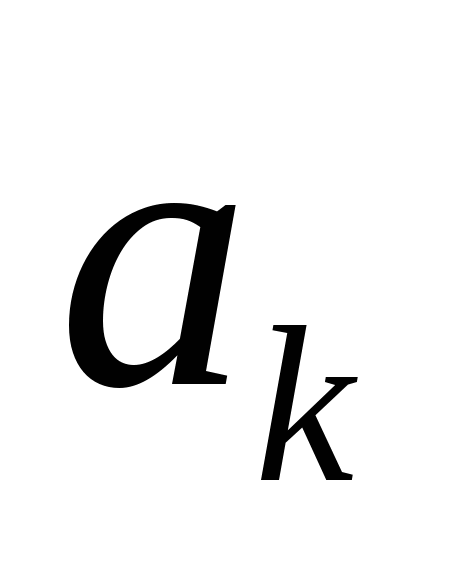 – числа, зависящие от индекса k, называется рядом (числовым рядом). – числа, зависящие от индекса k, называется рядом (числовым рядом).
Определение 19.2. Конечные суммы 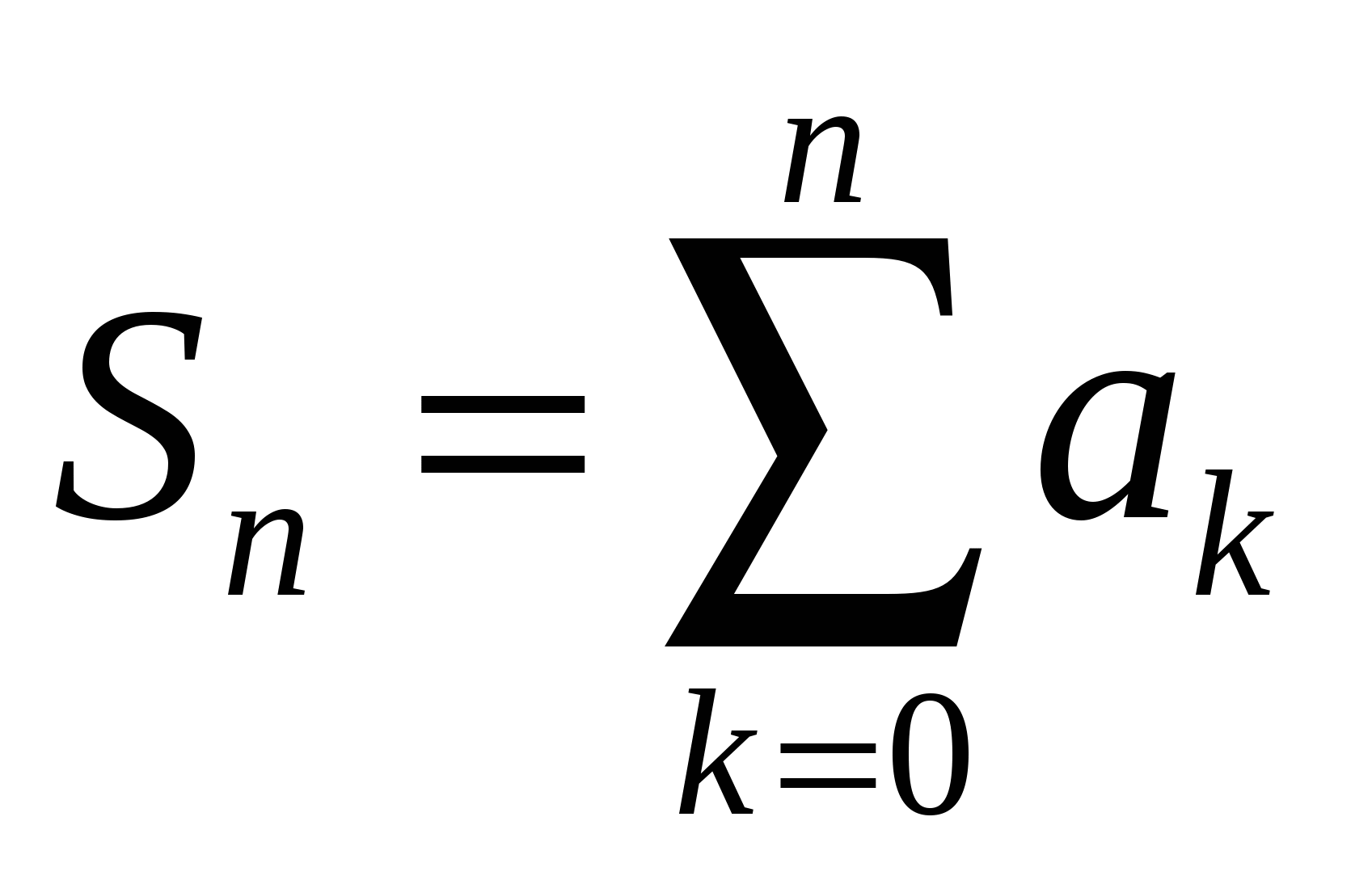 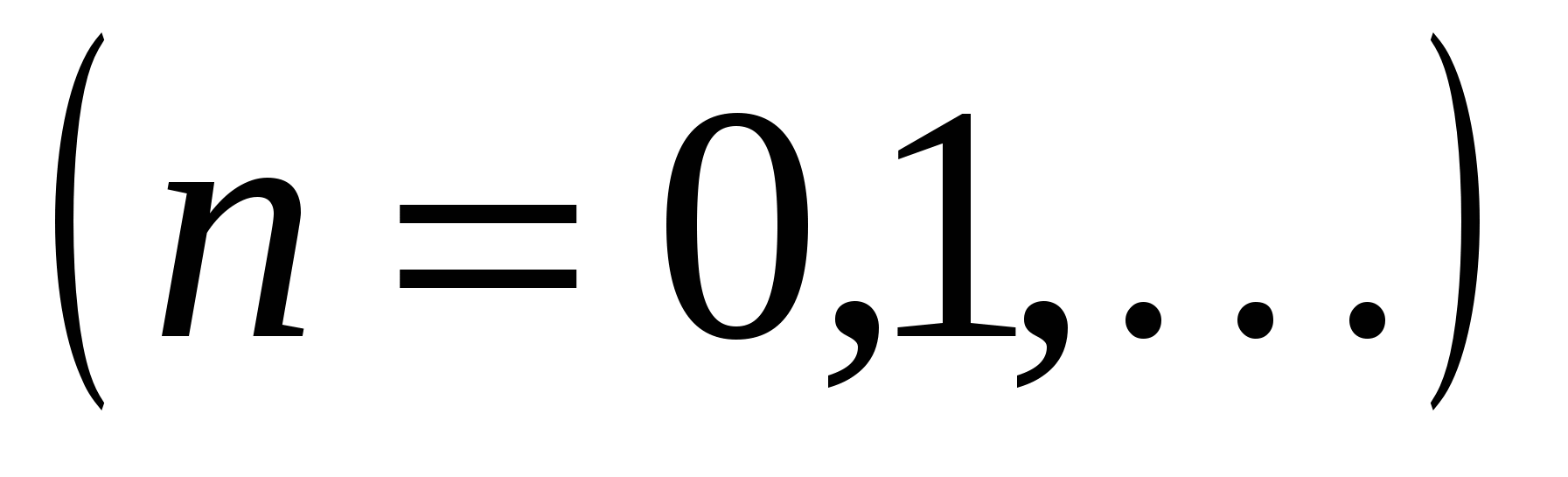 называются частичными суммами ряда (19.7). называются частичными суммами ряда (19.7).
Определение 19.3. Если существует конечный предел
 , (19.8) , (19.8)
то говорят, что ряд (19.7) сходится к числуS и называют Sсуммой ряда:
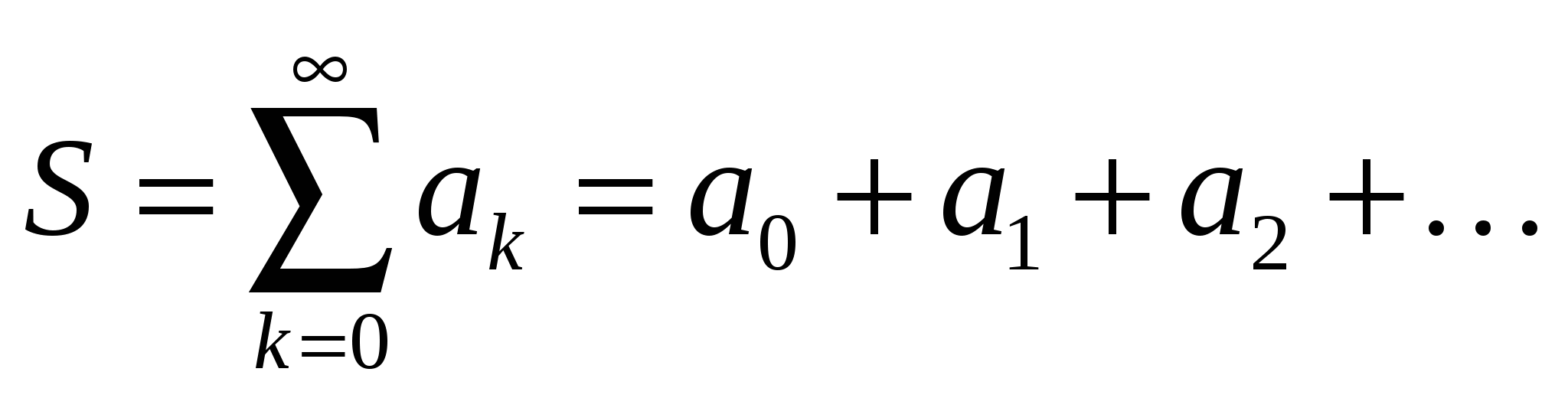 . .
Определение 19.4. Если предел частичных сумм Sn 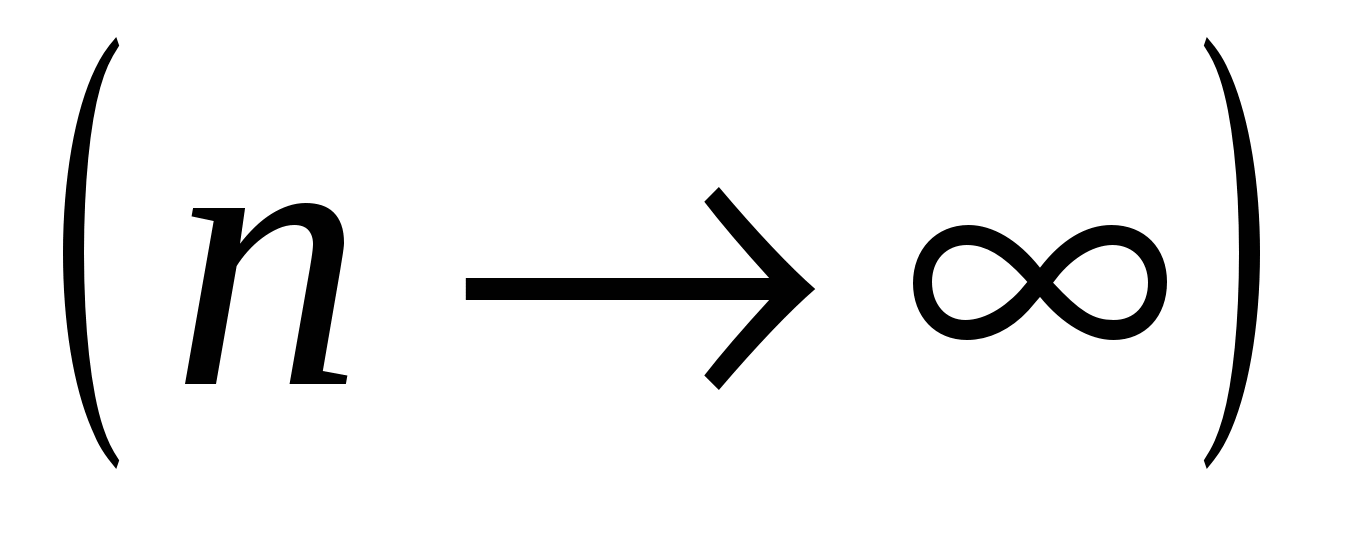 ряда (19.7) не существует или равен ряда (19.7) не существует или равен 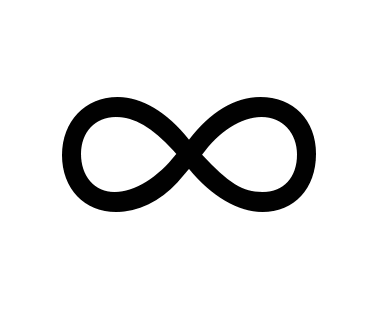 , то ряд (19.7) называется расходящимся рядом. , то ряд (19.7) называется расходящимся рядом.
Если функция 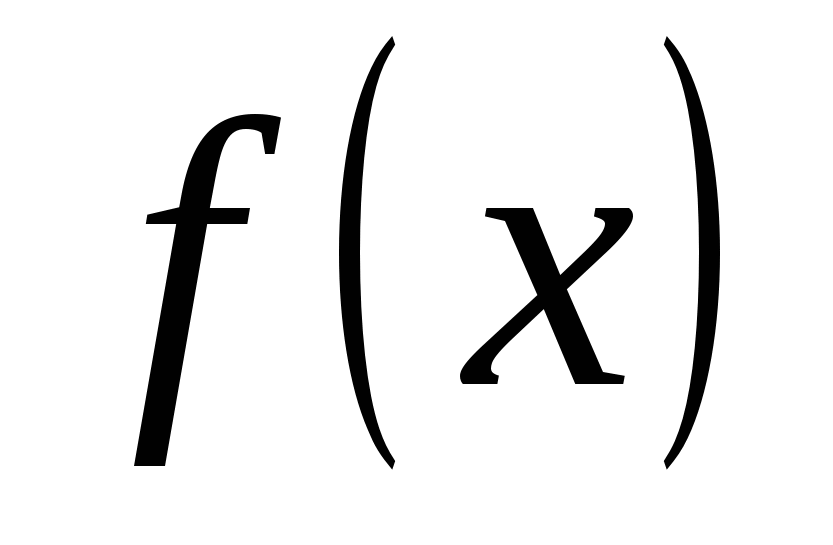 имеет производные любого порядка в окрестности точки имеет производные любого порядка в окрестности точки 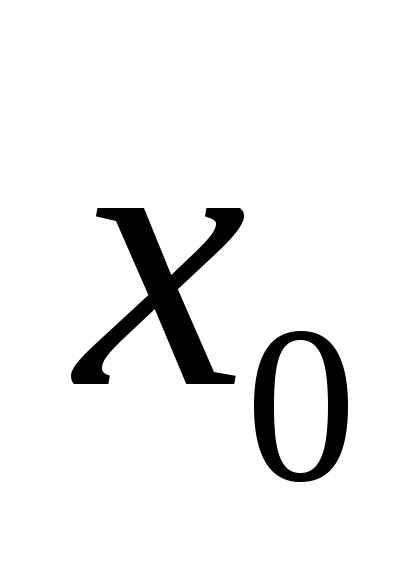 , то можно функцию , то можно функцию 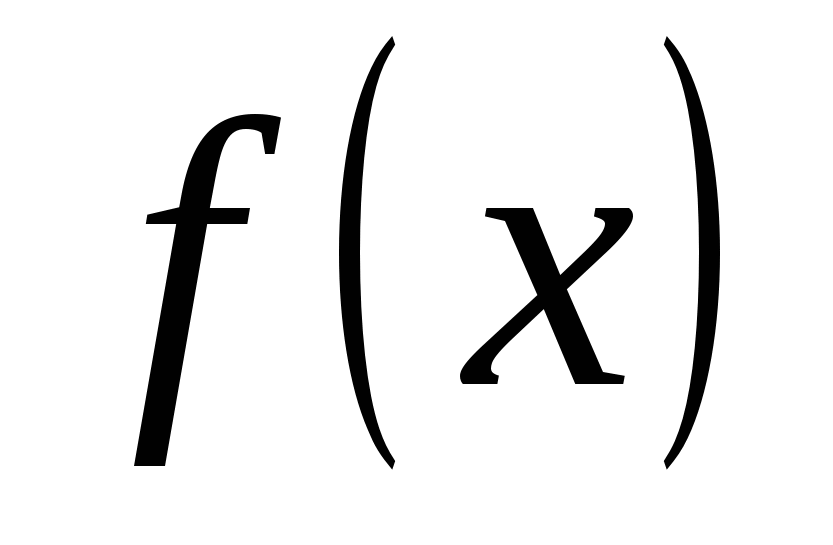 представить в виде суммы представить в виде суммы
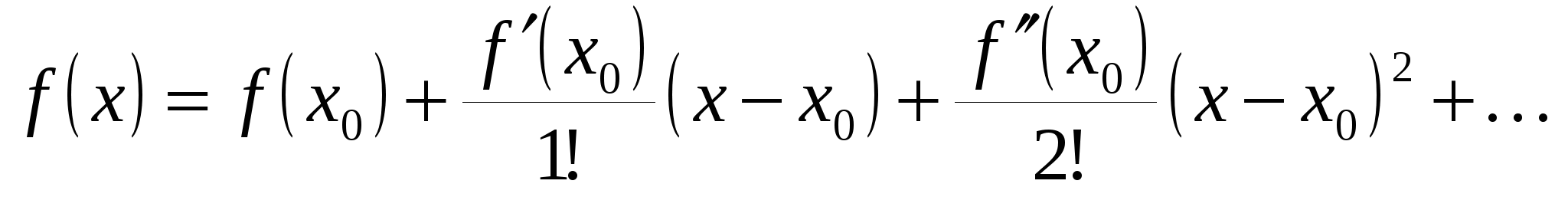 . .
Такое разложение называется рядом Тейлора функции 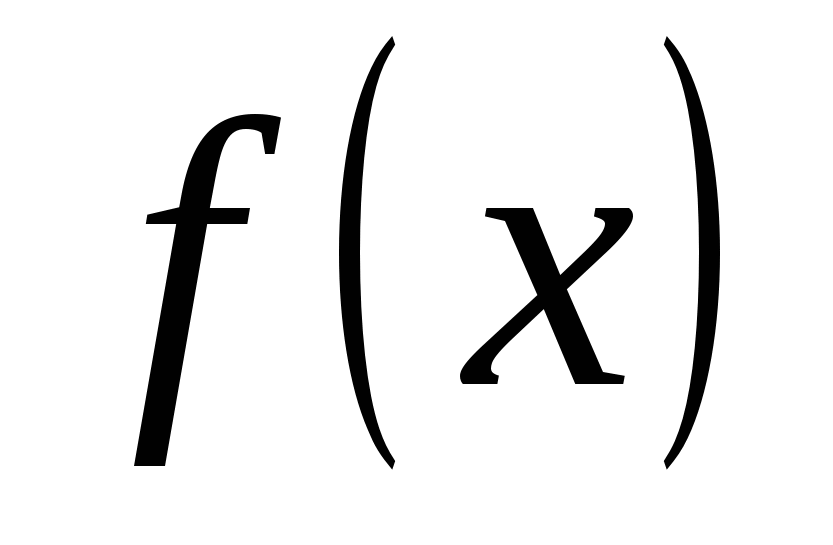 по степеням по степеням 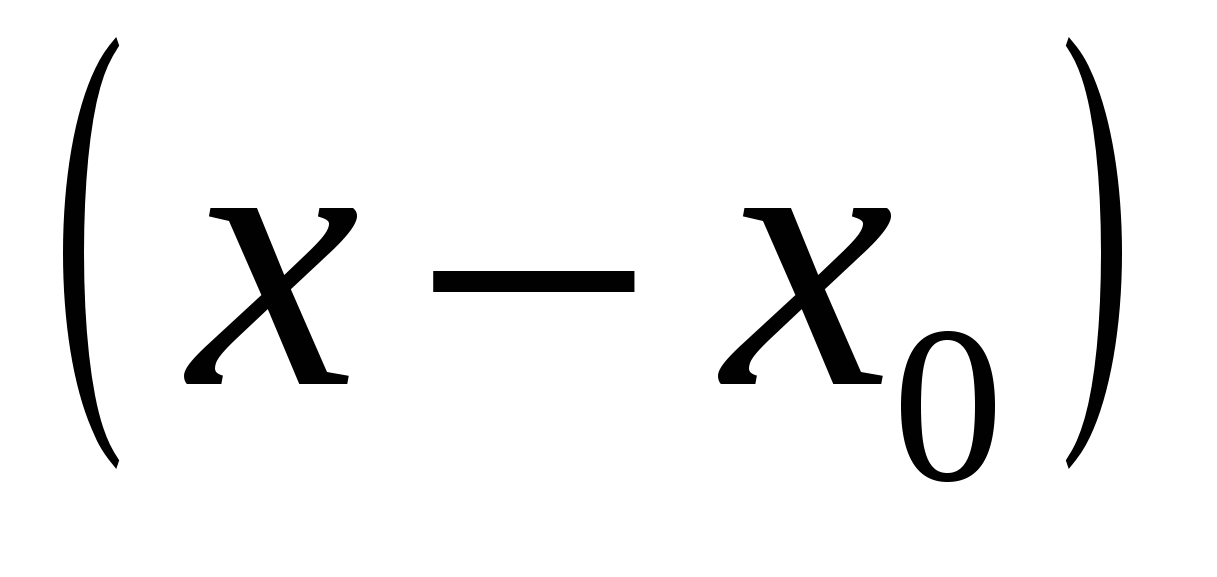 . Если . Если 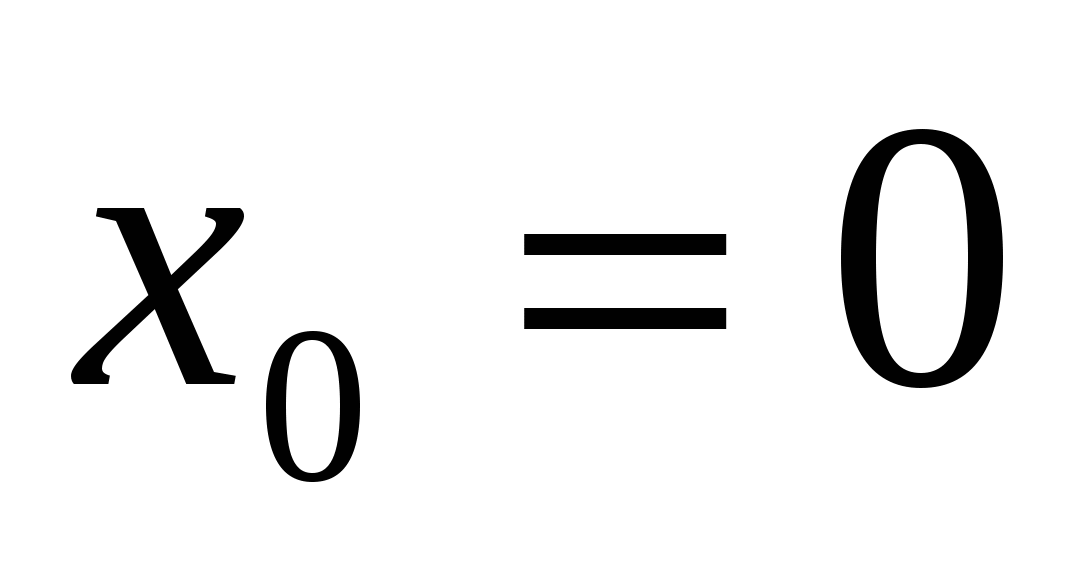 , то это будет ряд Маклорена. , то это будет ряд Маклорена.
Особый интерес представляет тот случай, когда ряд Тейлора функции 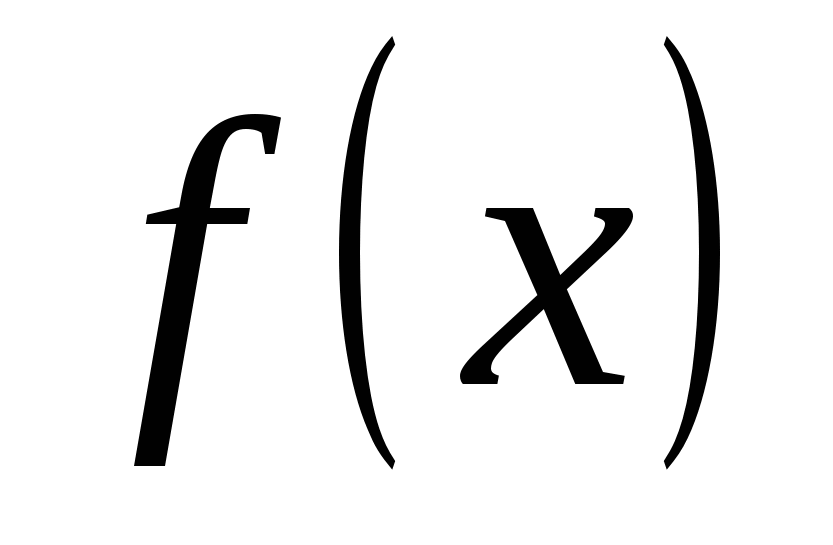 по степеням по степеням 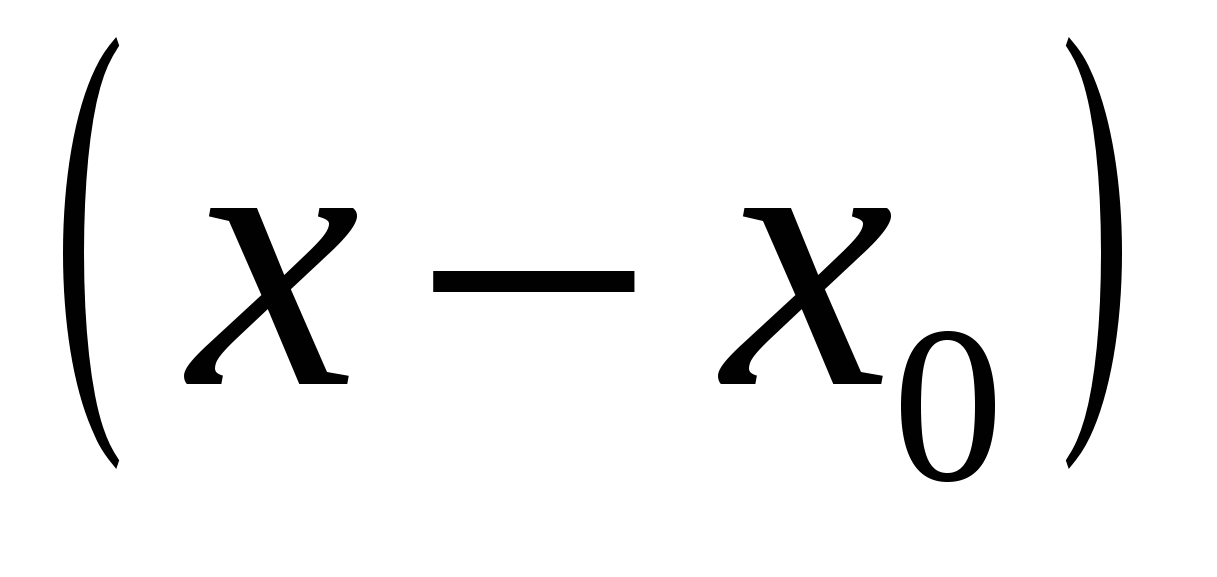 сходится в некоторой окрестности точки сходится в некоторой окрестности точки 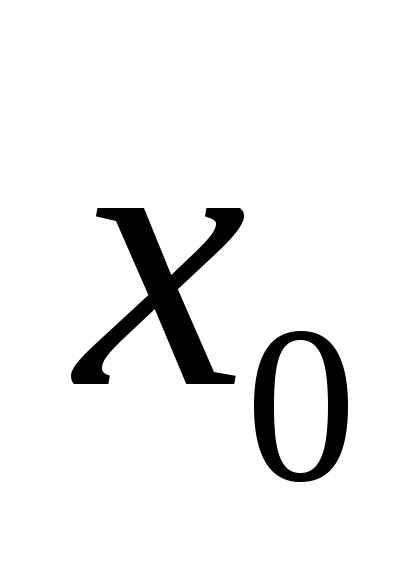 и при том к самой функции и при том к самой функции 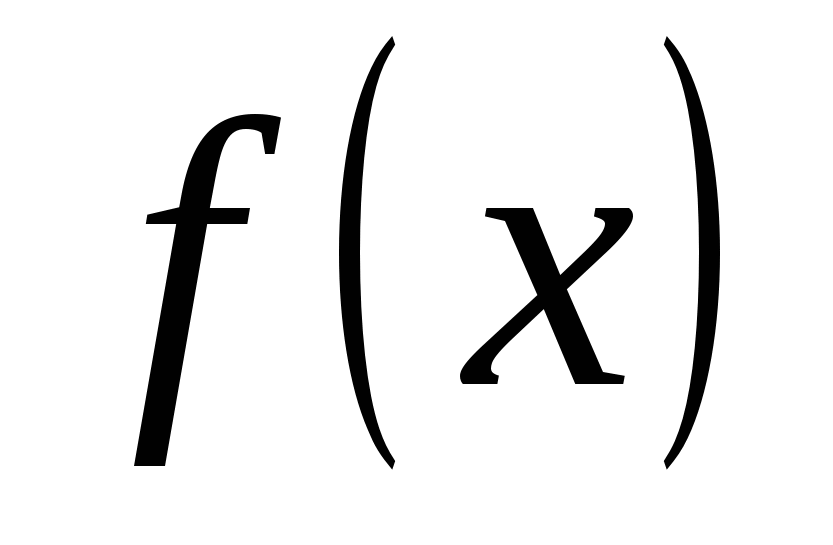 . Если это имеет место, то . Если это имеет место, то
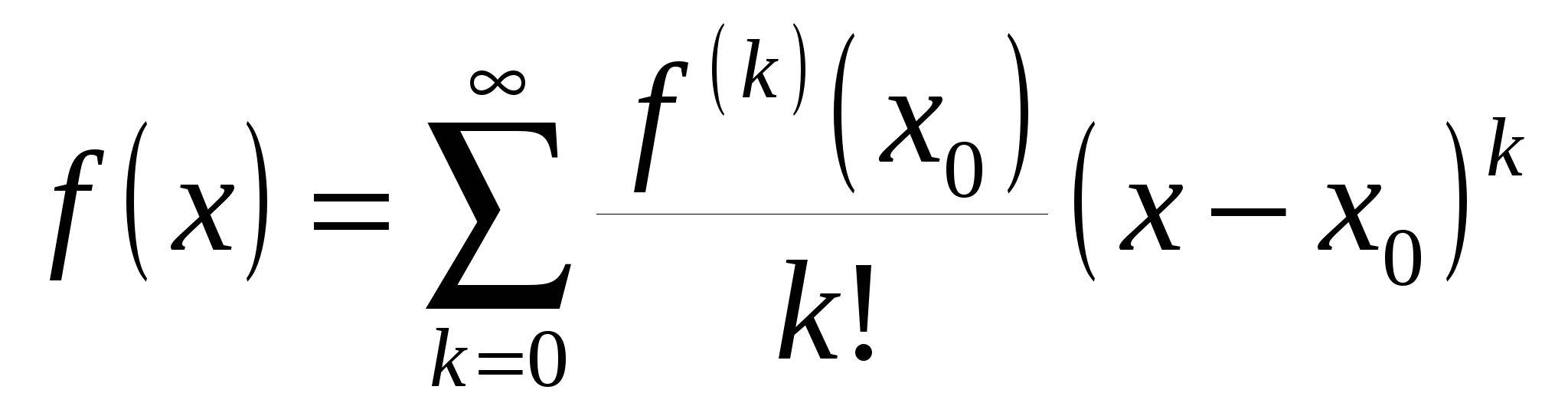 , , 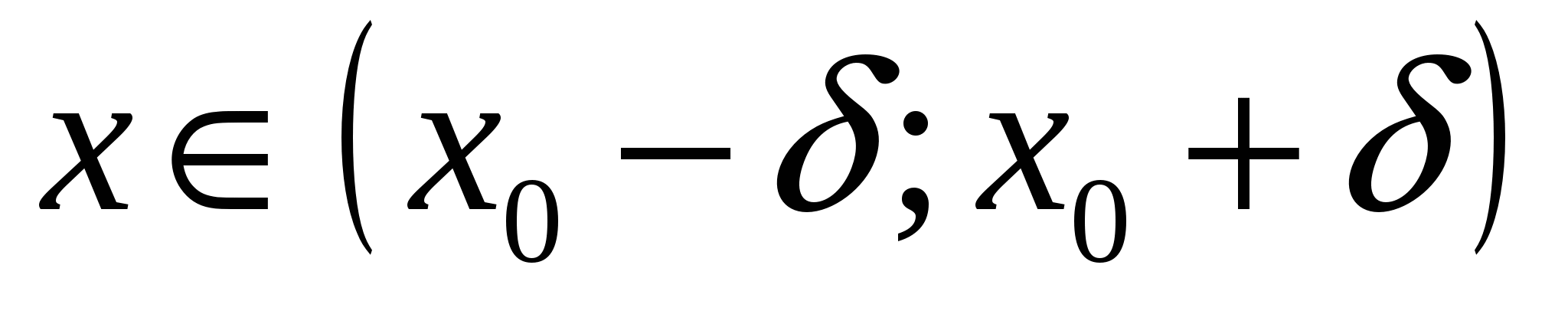 , (19.9) , (19.9)
то есть функция 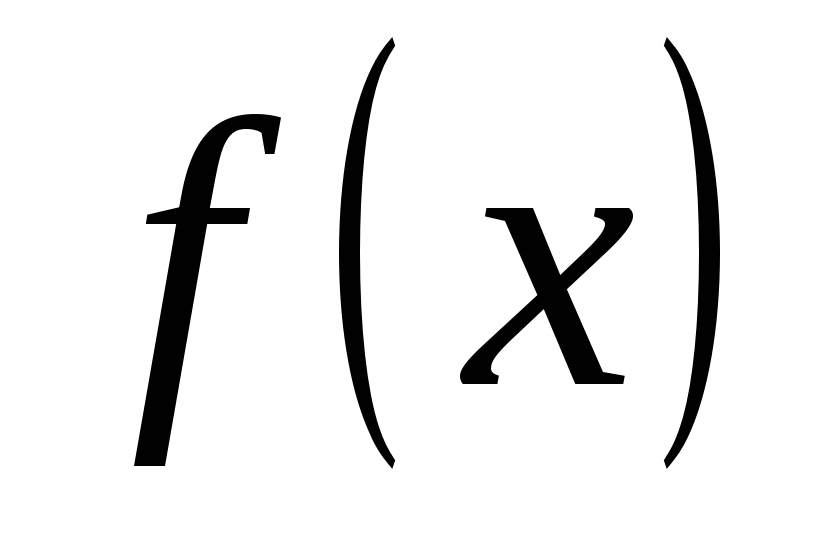 есть сумма её ряда Тейлора в некоторой окрестности точки есть сумма её ряда Тейлора в некоторой окрестности точки 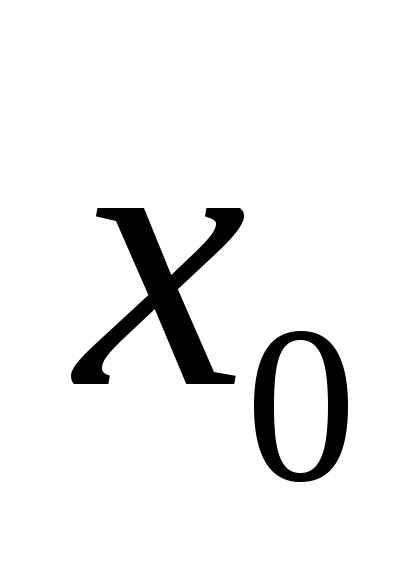 . В этом случае говорят, что функция . В этом случае говорят, что функция 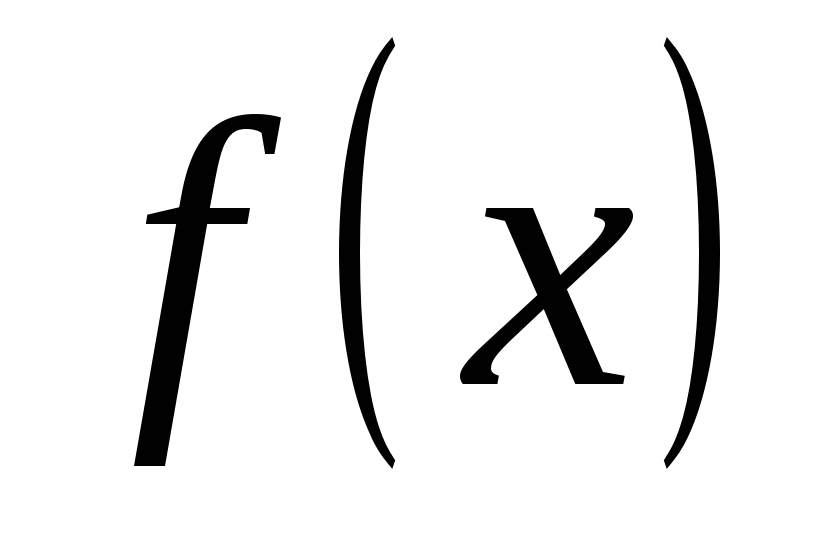 разлагается в ряд Тейлора по степеням разлагается в ряд Тейлора по степеням 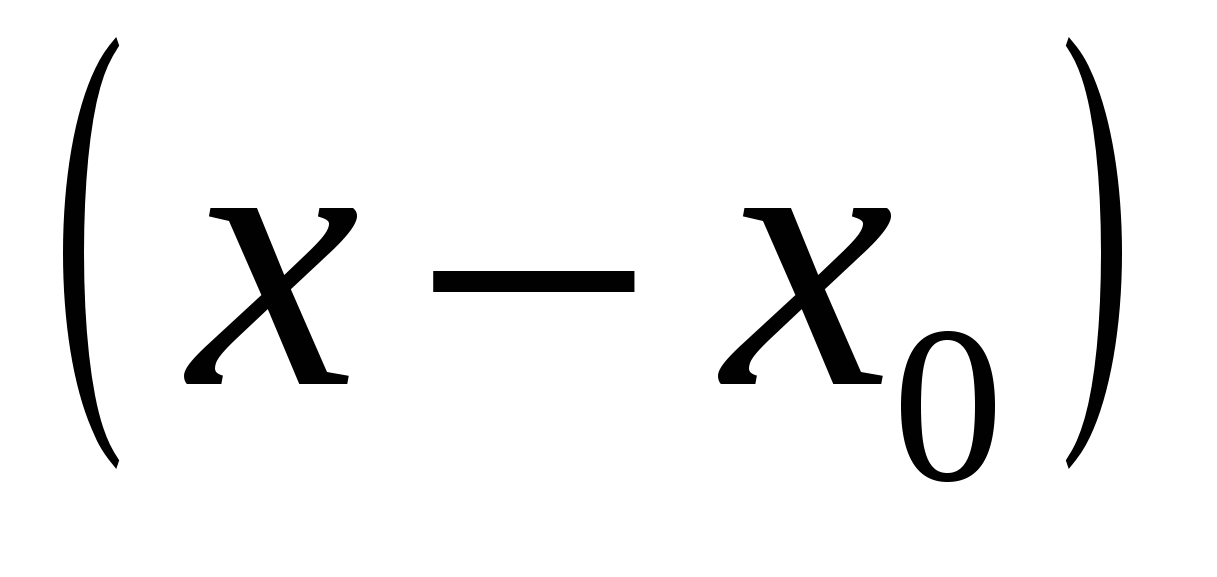 , сходящийся к ней. , сходящийся к ней.
♦ Теорема 19.1. Пусть функция 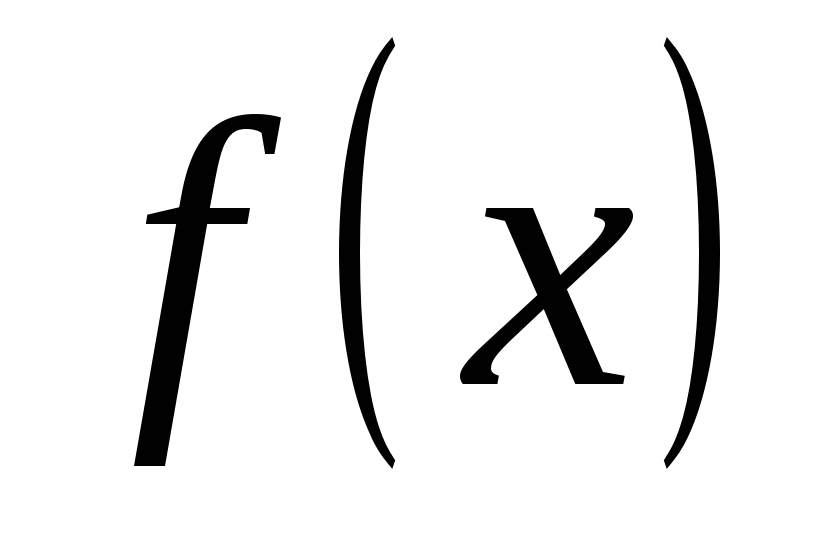 на отрезке на отрезке 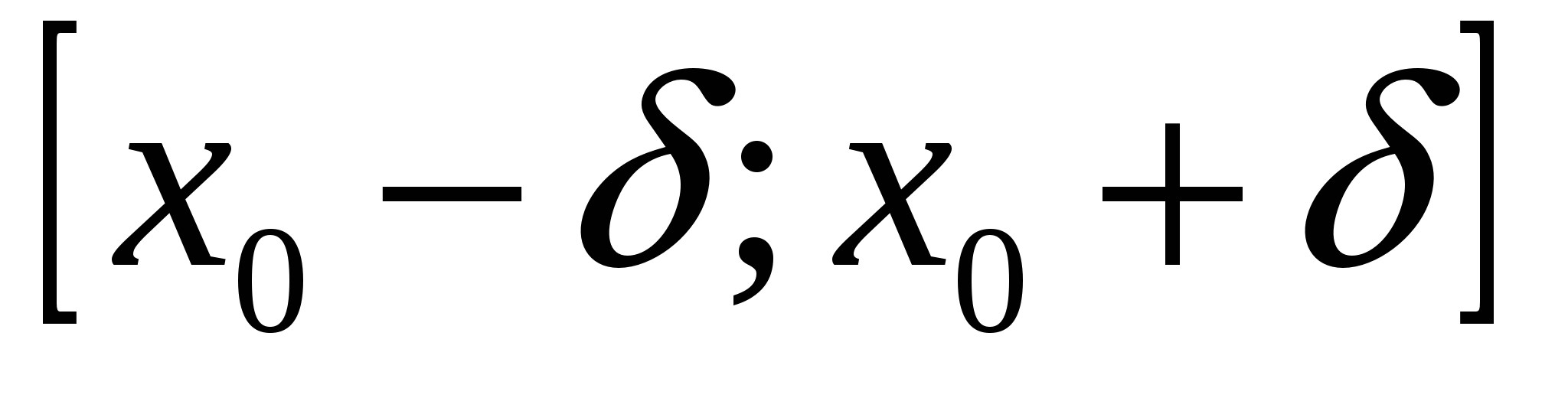 имеет производные любого порядка и остаток её формулы Тейлора стремится к нулю при имеет производные любого порядка и остаток её формулы Тейлора стремится к нулю при  на этом отрезке: на этом отрезке:
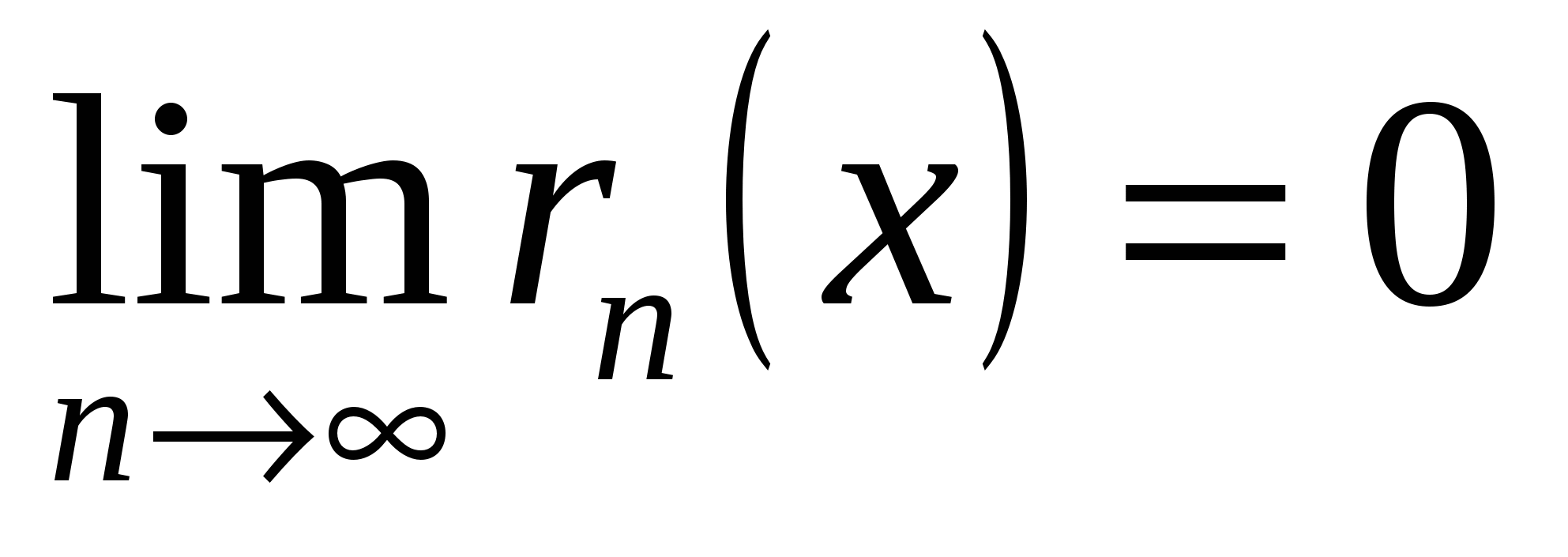 . (19.10) . (19.10)
Тогда функция 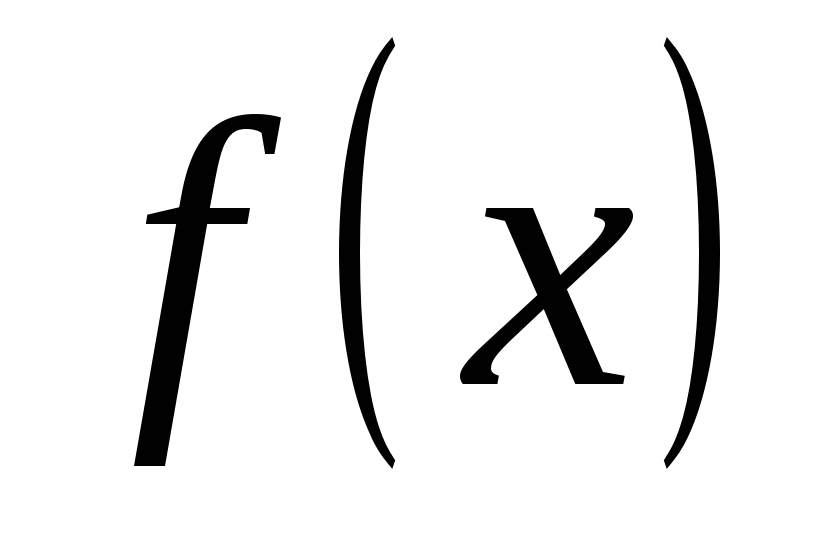 разлагается в ряд Тейлора на этом отрезке. разлагается в ряд Тейлора на этом отрезке.
Доказательство. Пусть функция 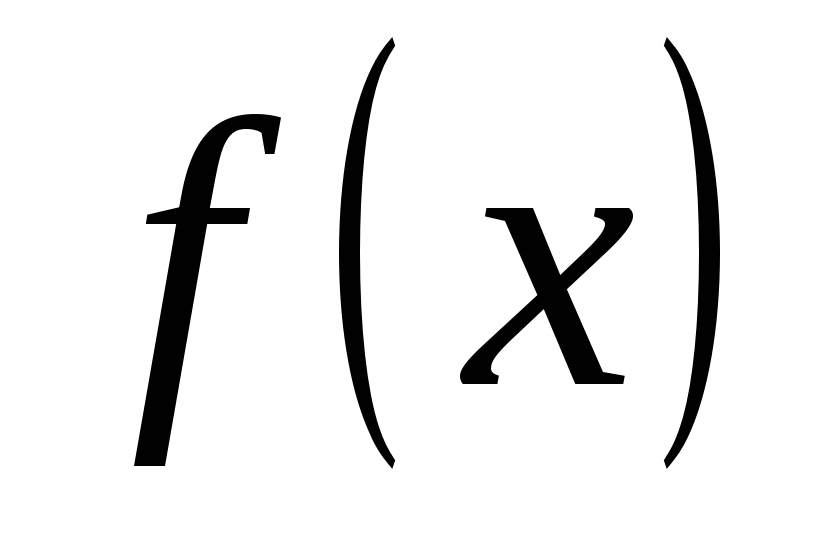 имеет на отрезке имеет на отрезке 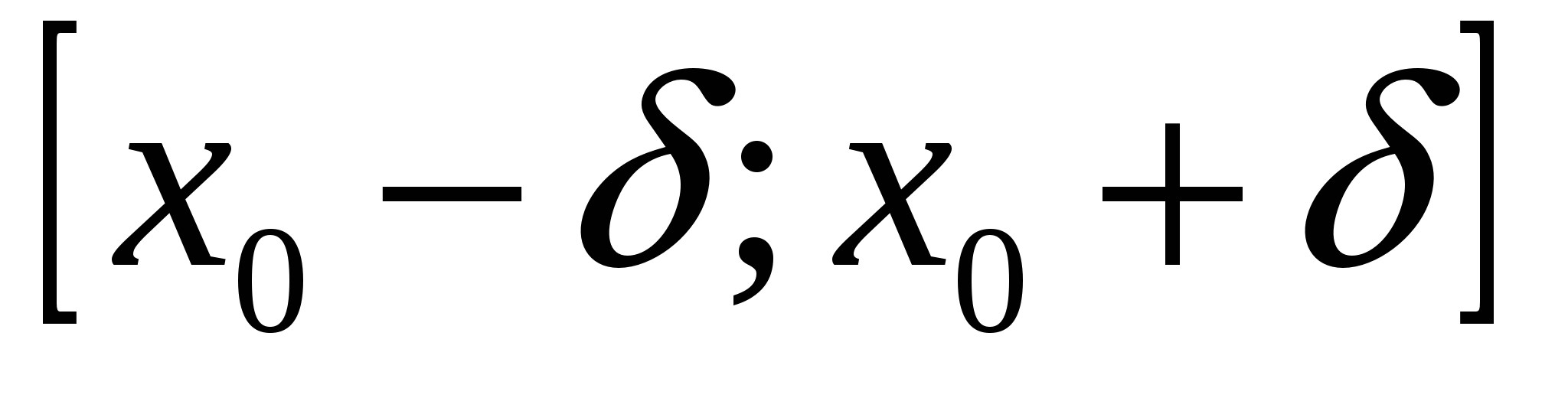 производные любого порядка. Тогда эти производные непрерывны на производные любого порядка. Тогда эти производные непрерывны на 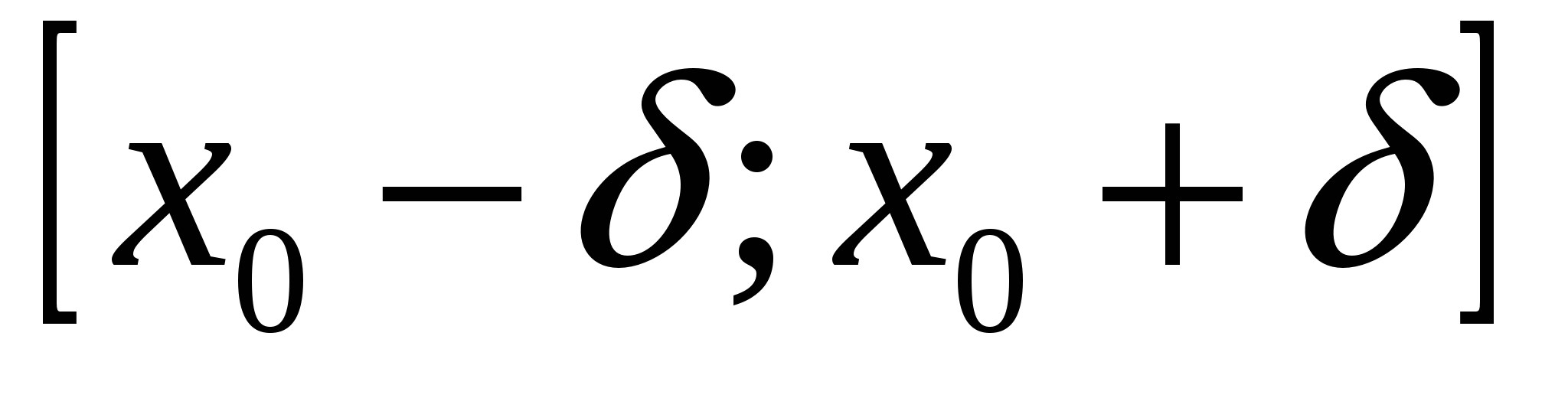 , потому что если , потому что если 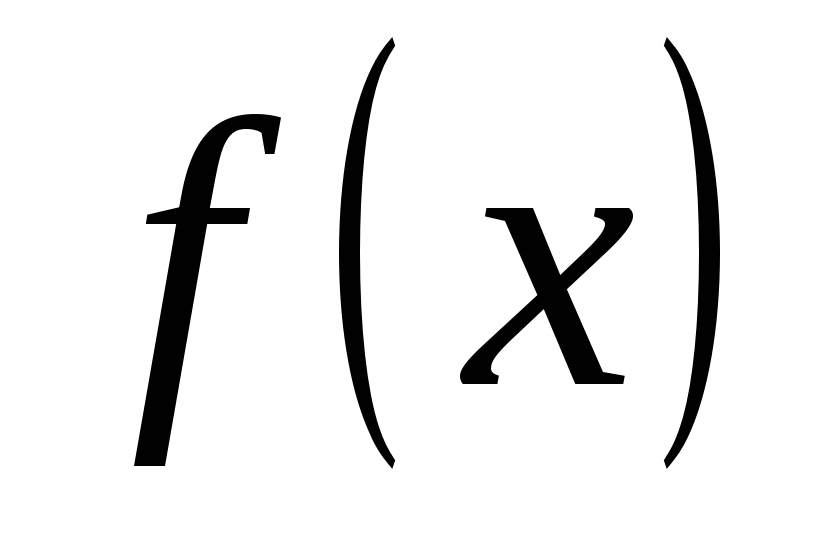 имеет производную имеет производную 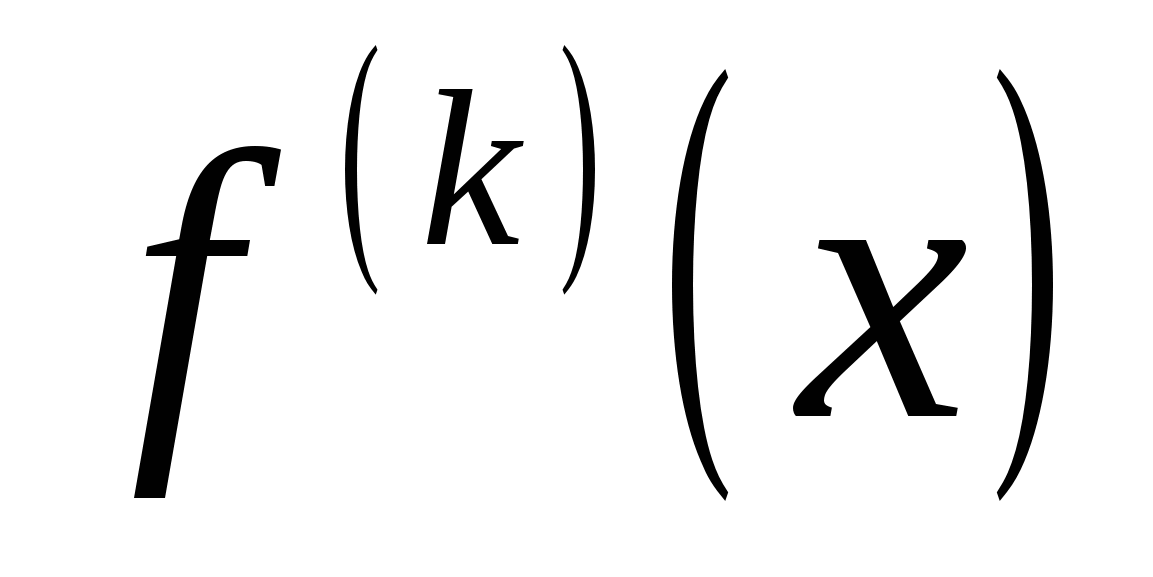 на на 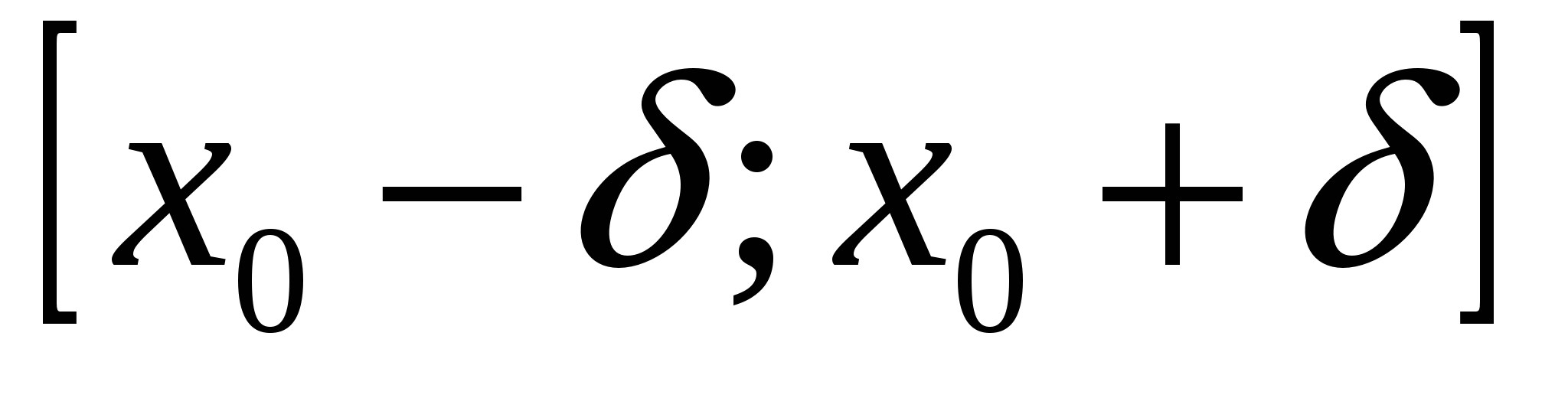 , то производная , то производная 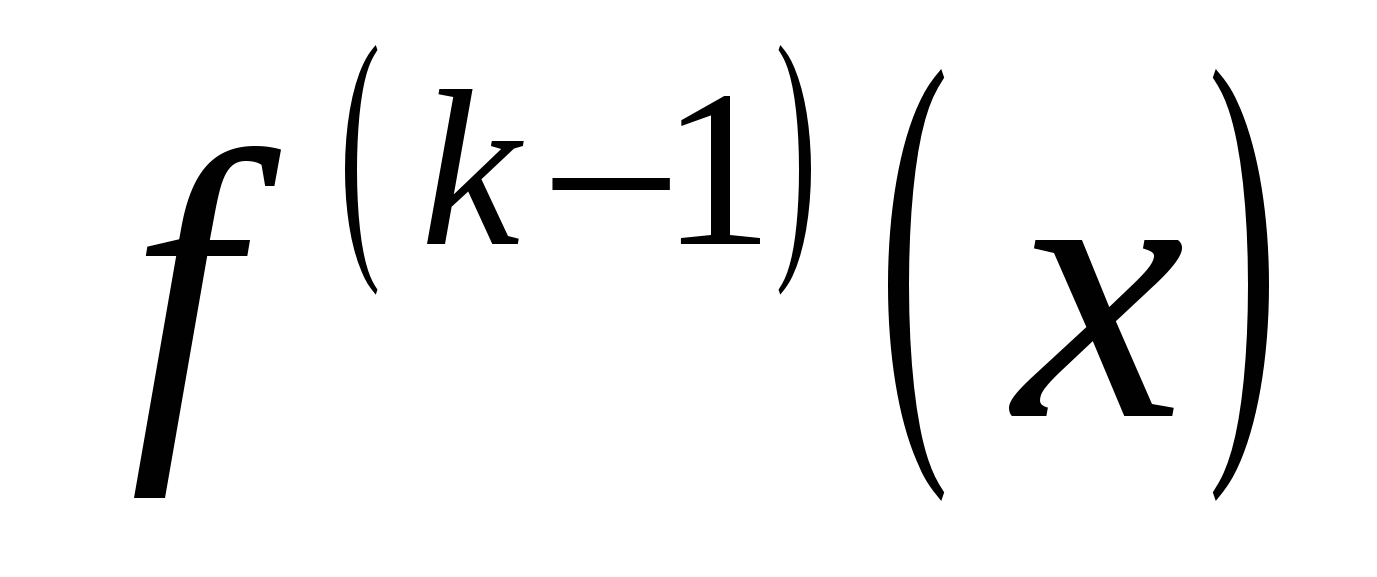 непрерывна на непрерывна на 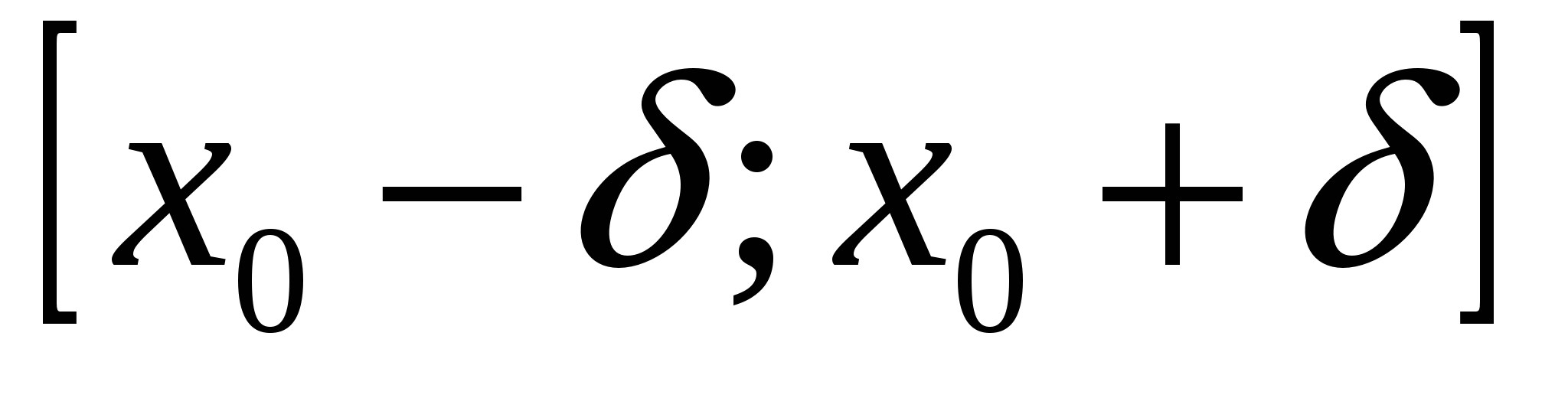 . .
Поэтому для нашей функции 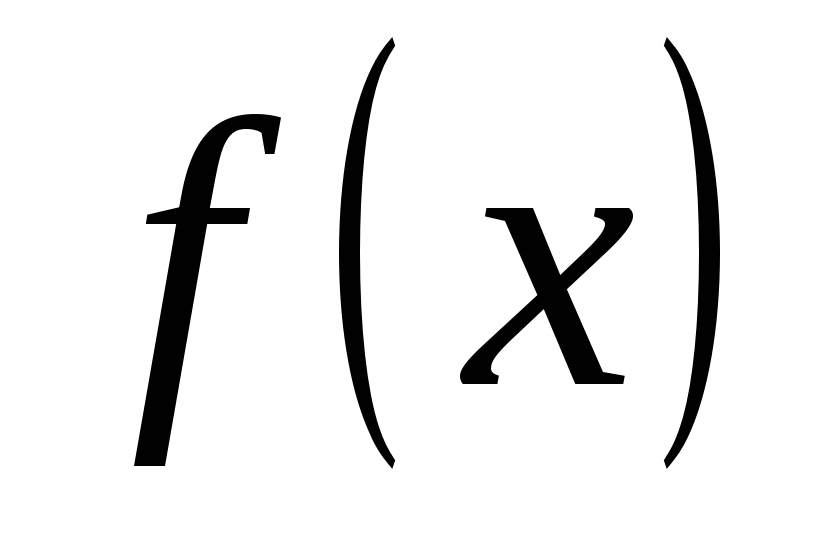 имеет смысл формула Тейлора: имеет смысл формула Тейлора:
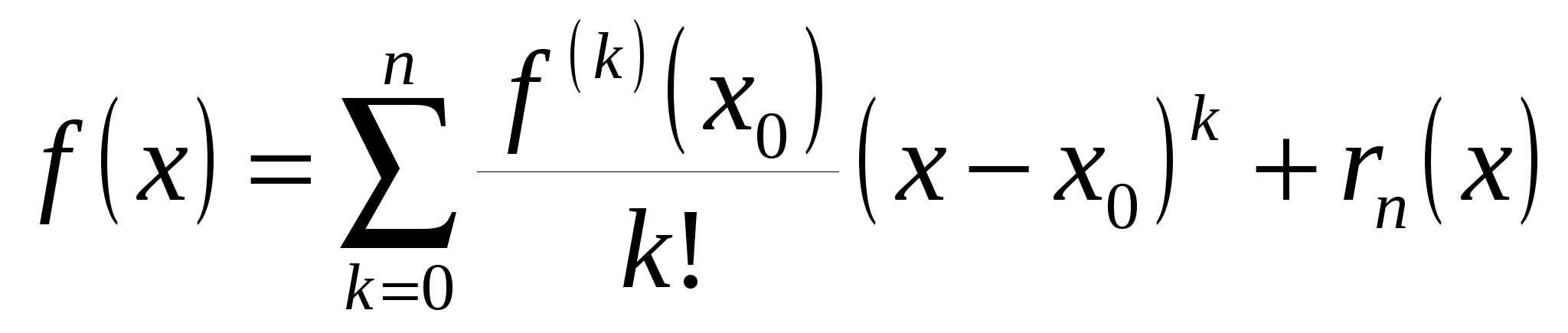 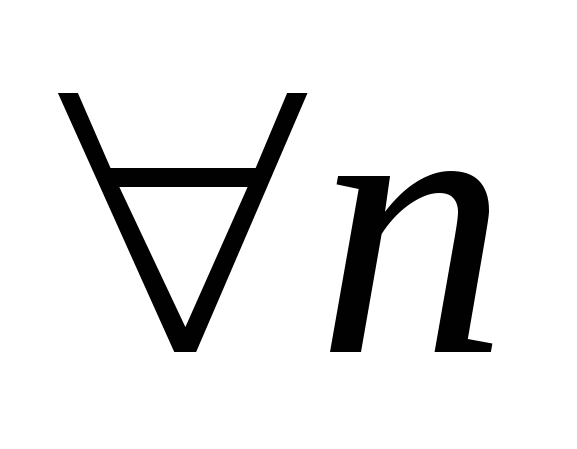 , , 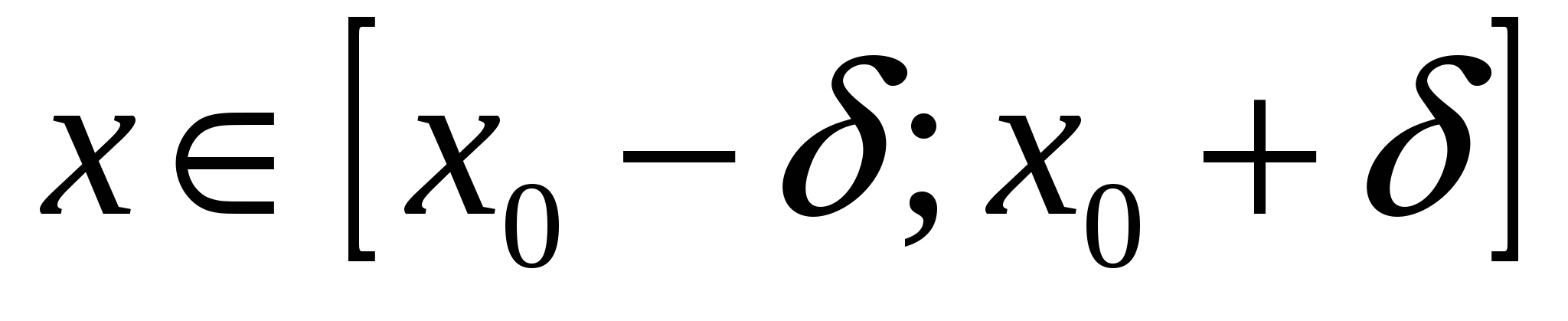 . .
В силу (19.10)
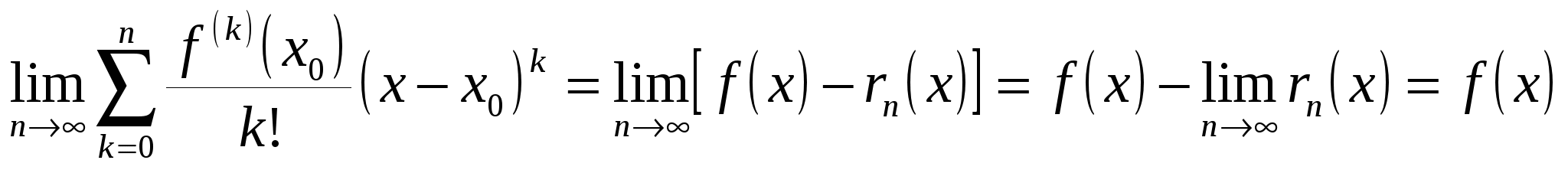 . .
То есть в этом случае многочлен Тейлора функции 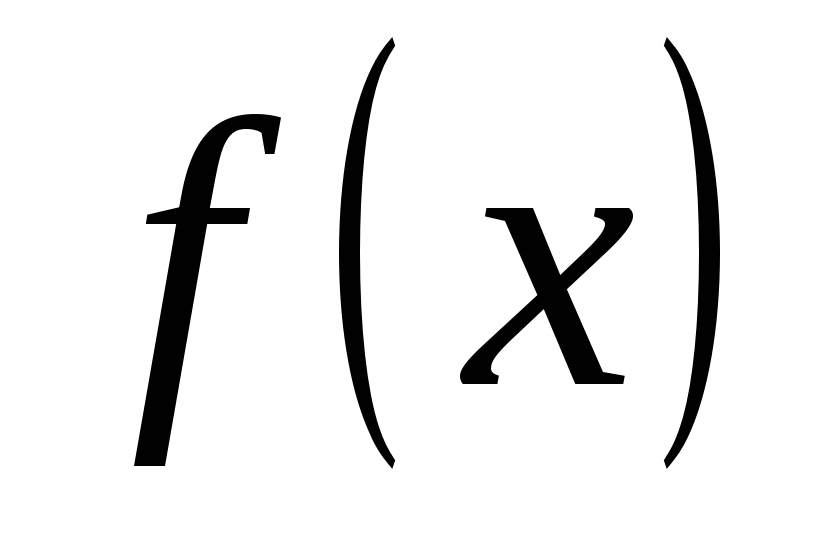 по степеням по степеням 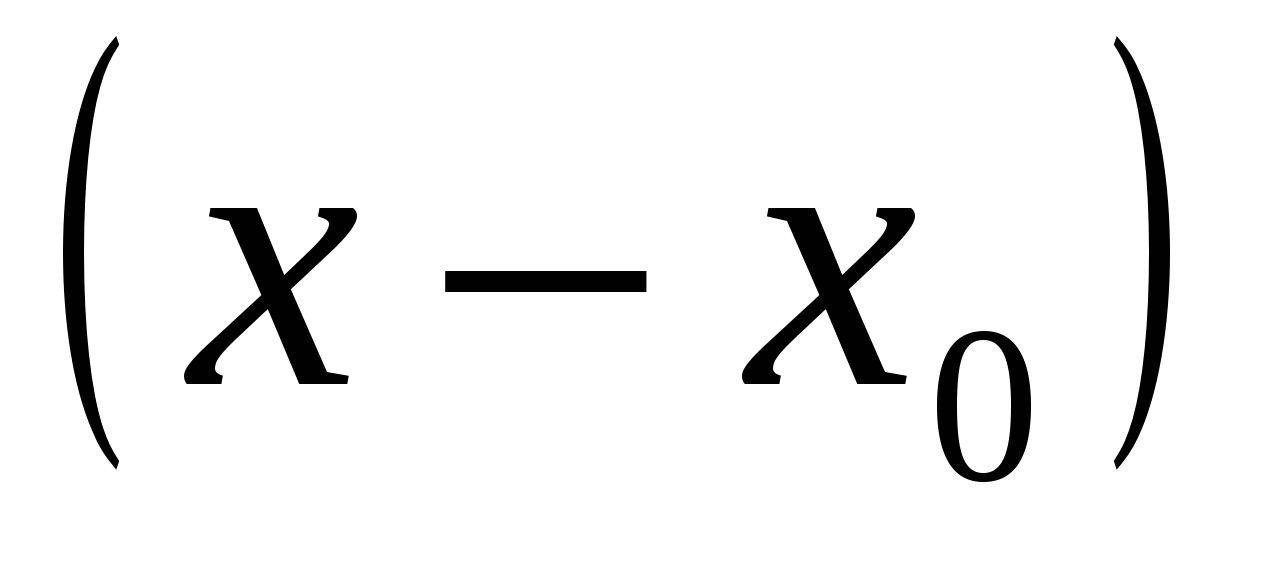 стремится при стремится при  к самой функции: к самой функции:
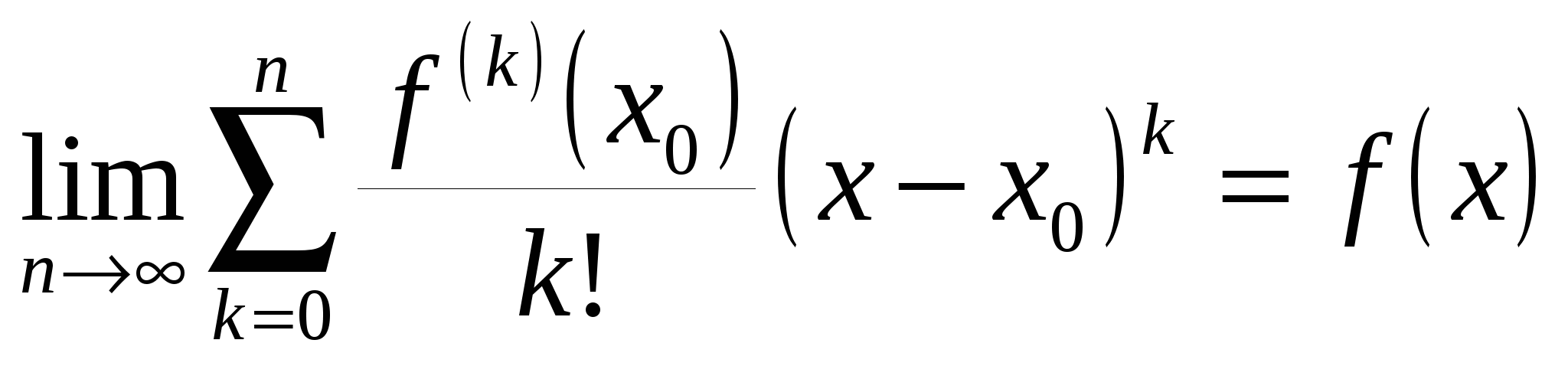 , , 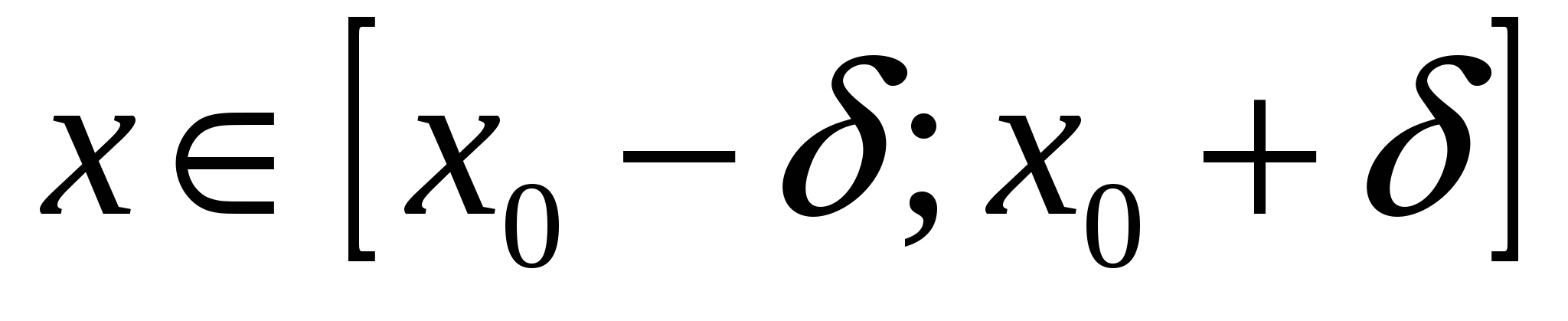 . (19.11) . (19.11)
А это означает, что ряд Тейлора функции 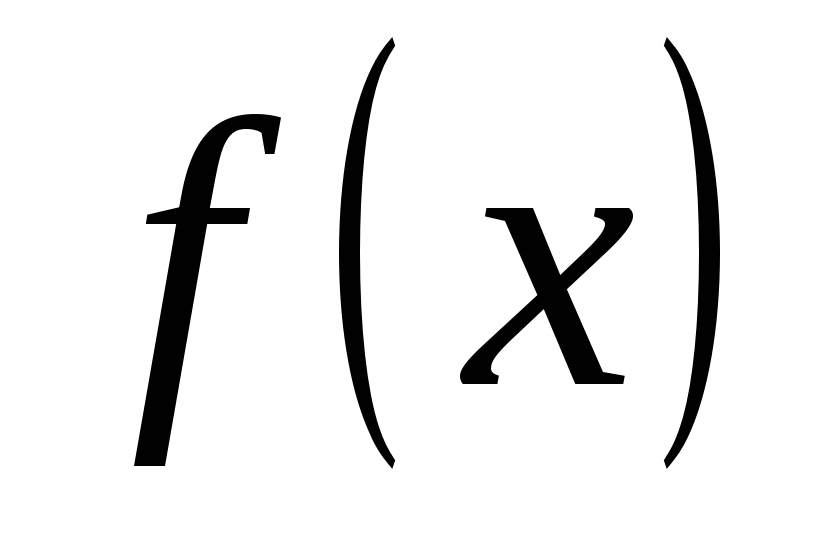 сходится на сходится на 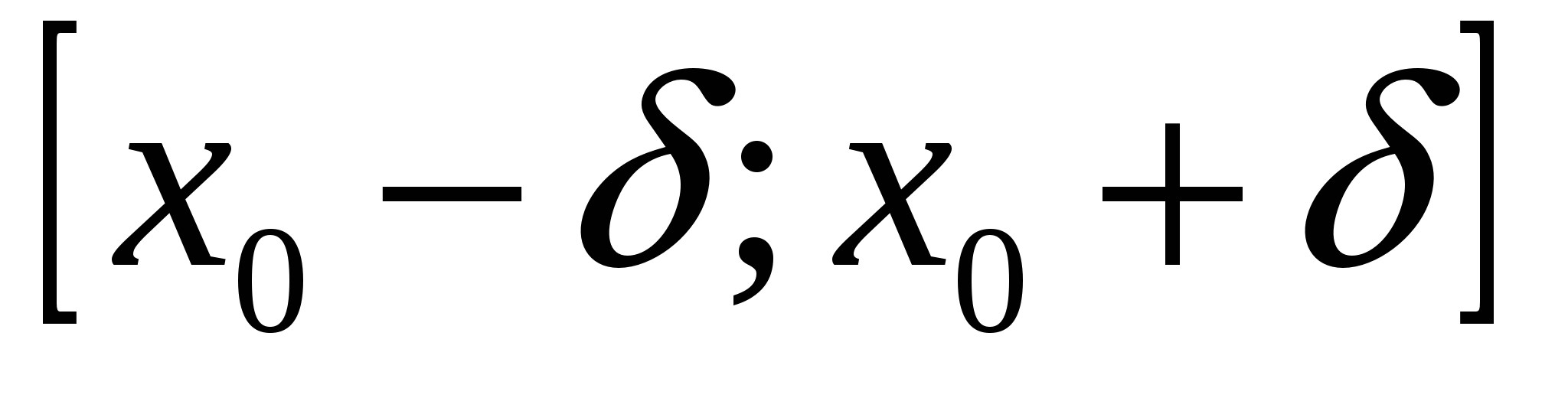 и имеет своей суммой и имеет своей суммой 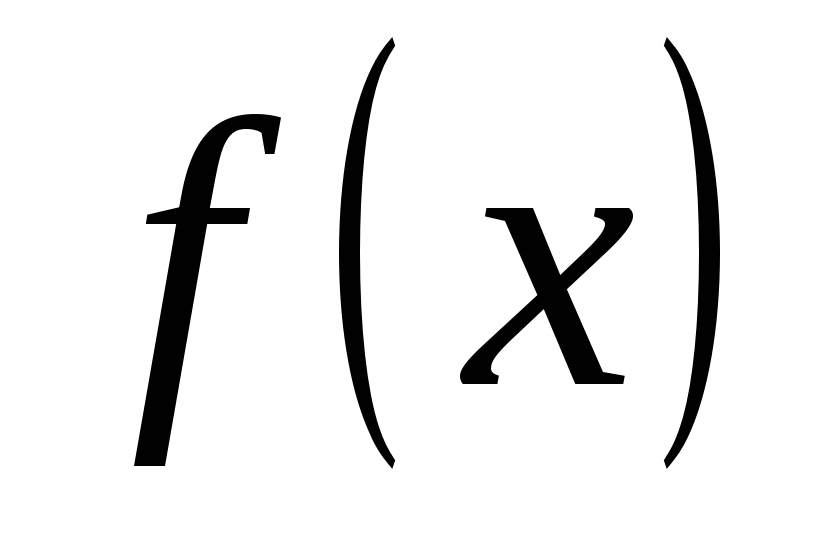 : :
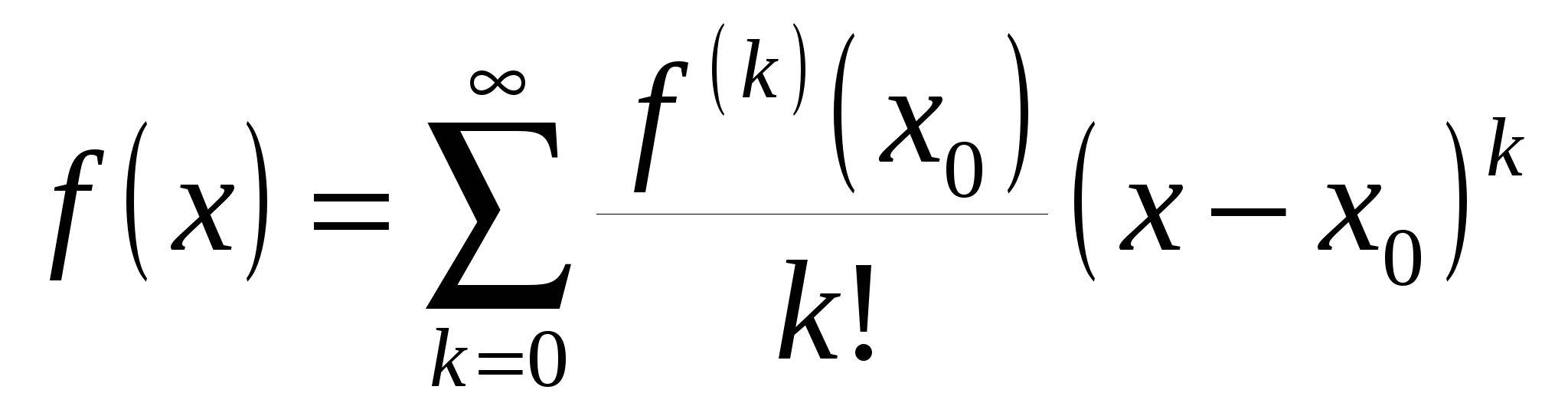 , , 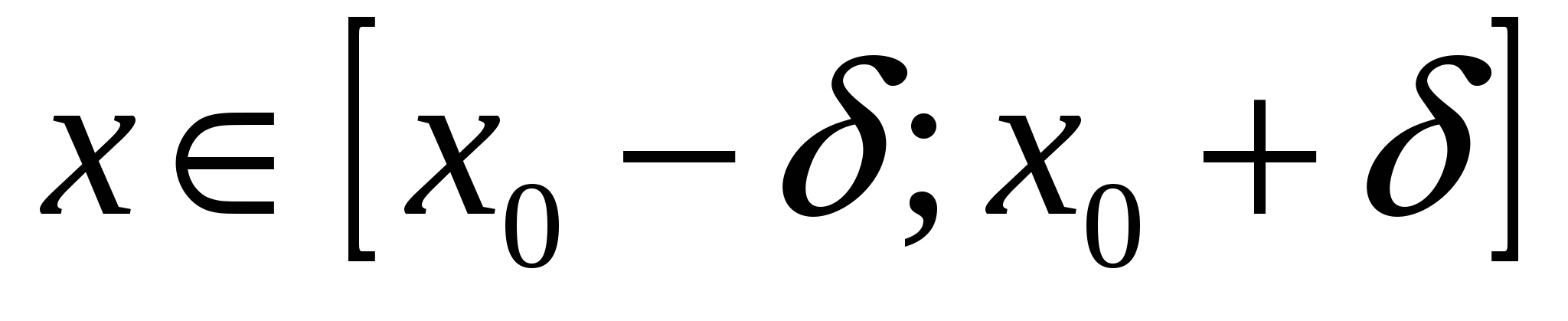 . ■ . ■
♦ Теорема 19.2 (достаточный критерий сходимости остатка формулы Тейлора к нулю). Если функция 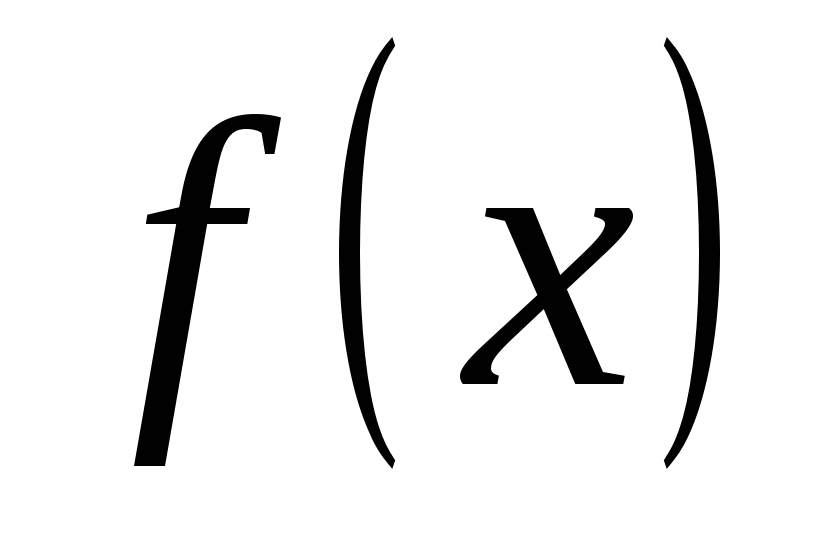 имеет на отрезке имеет на отрезке 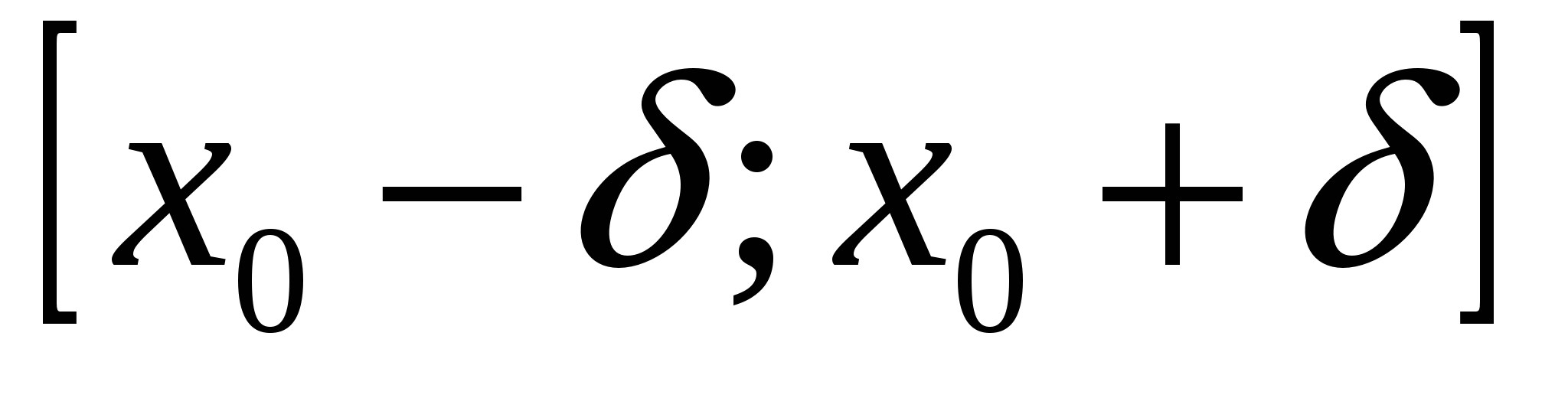 производные любого порядка, ограниченные одним и тем же числом производные любого порядка, ограниченные одним и тем же числом 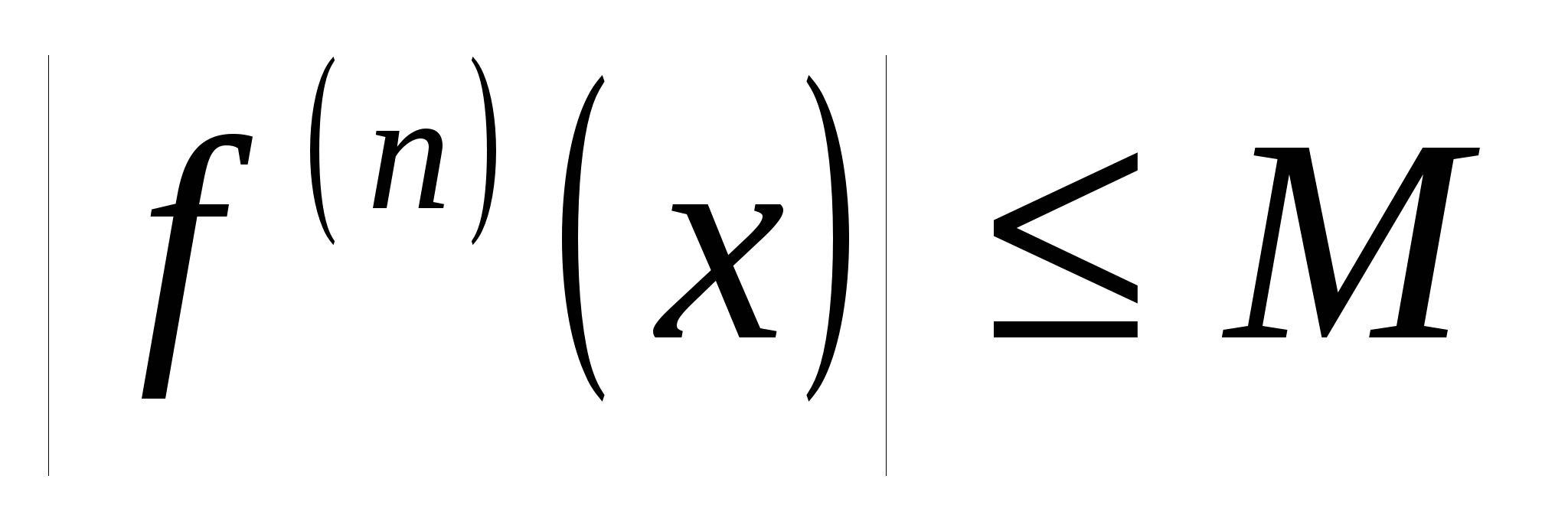 , , 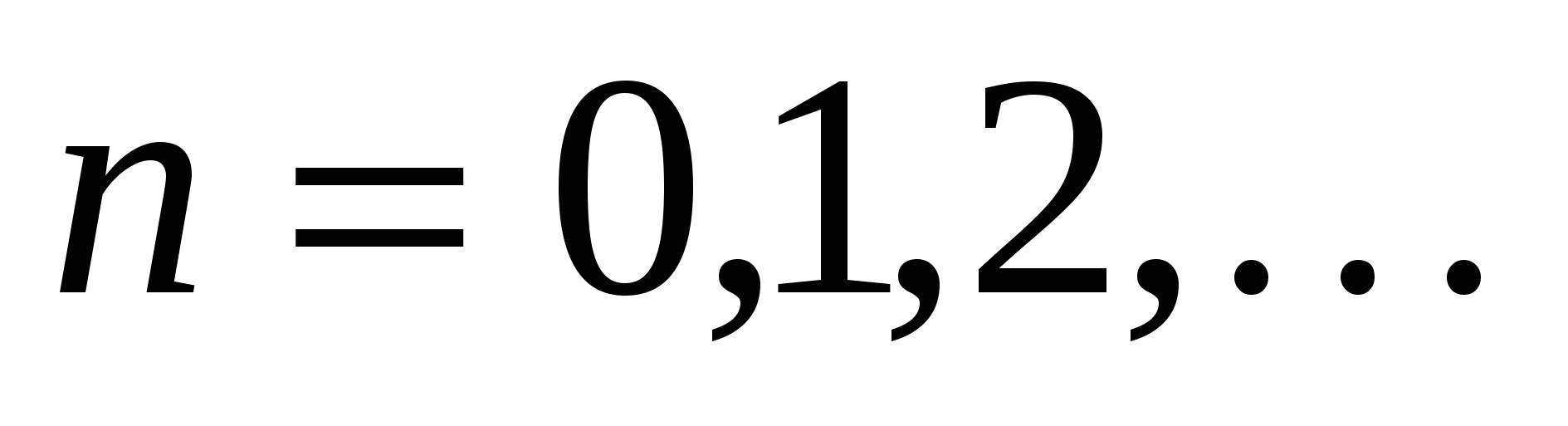 , то остаток её формулы Тейлора на этом отрезке стремится при , то остаток её формулы Тейлора на этом отрезке стремится при  к нулю: к нулю:
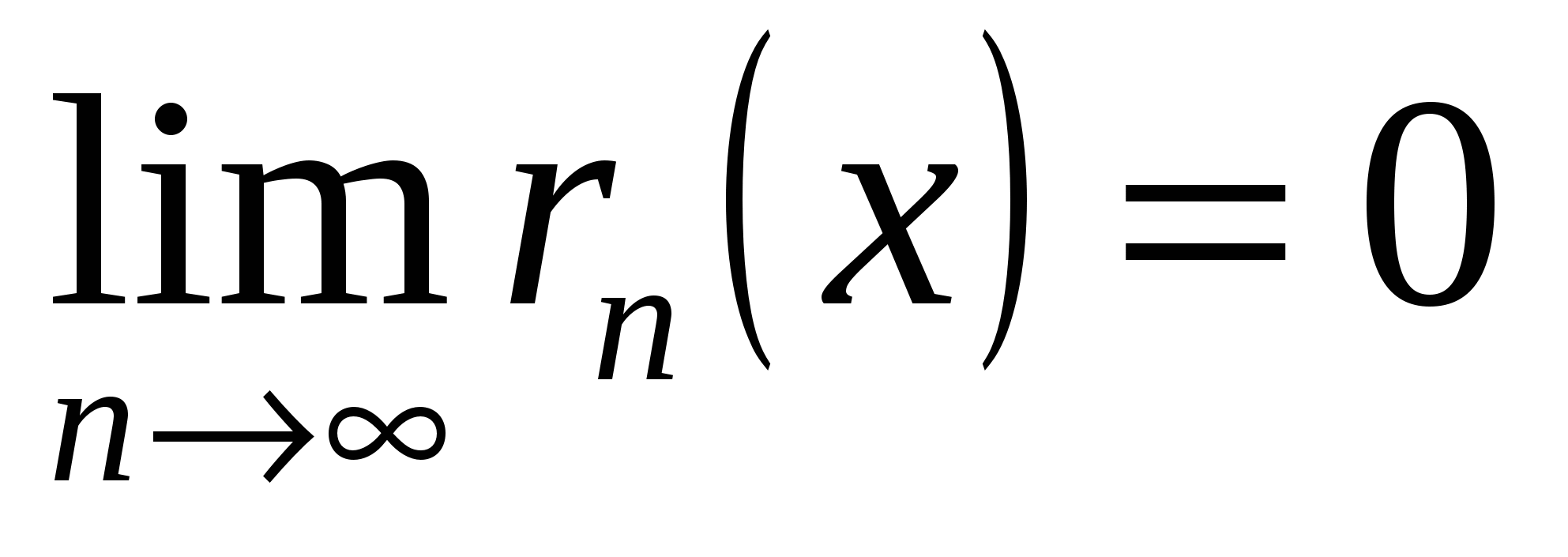 . (19.12) . (19.12)
Доказательство. Воспользуемся формой Лагранжа остаточного члена:
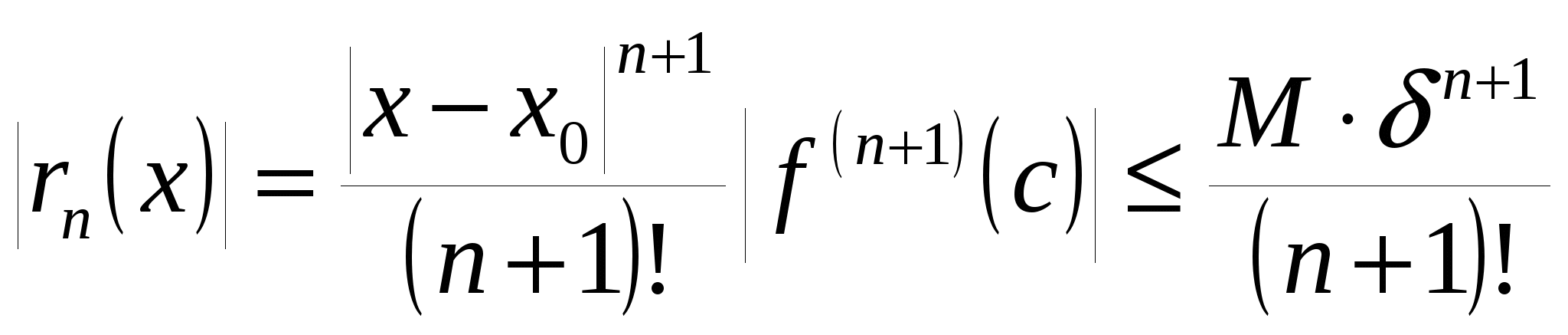 . (19.13) . (19.13)
Так как правая часть (19.13) стремится к нулю при  , то имеет место (19.12). ■ , то имеет место (19.12). ■
19.4. Формулы и ряды Тейлора элементарных функций.
1) 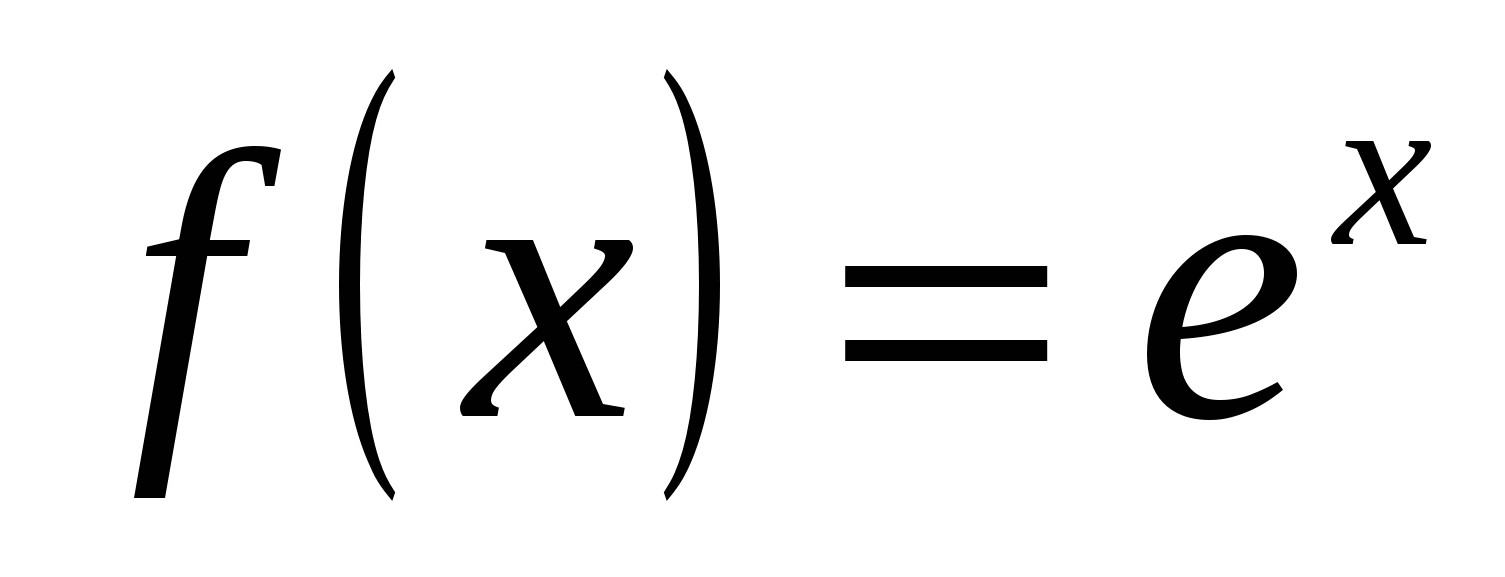 . Эта функция бесконечно дифференцируема на . Эта функция бесконечно дифференцируема на 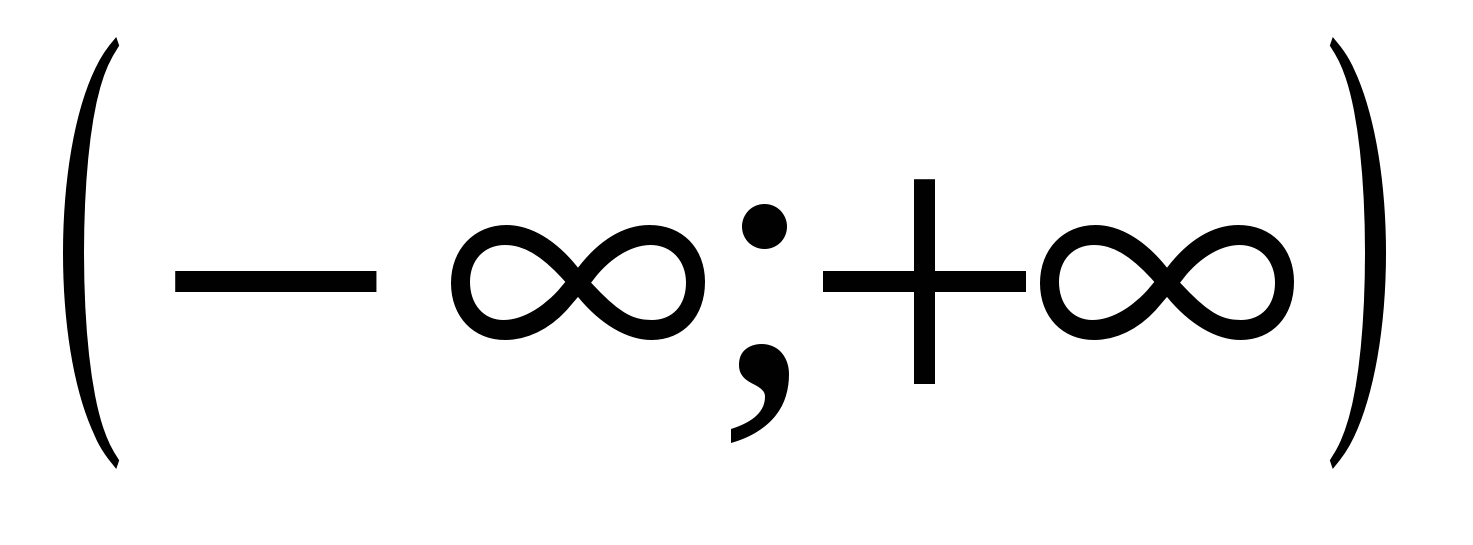 : :
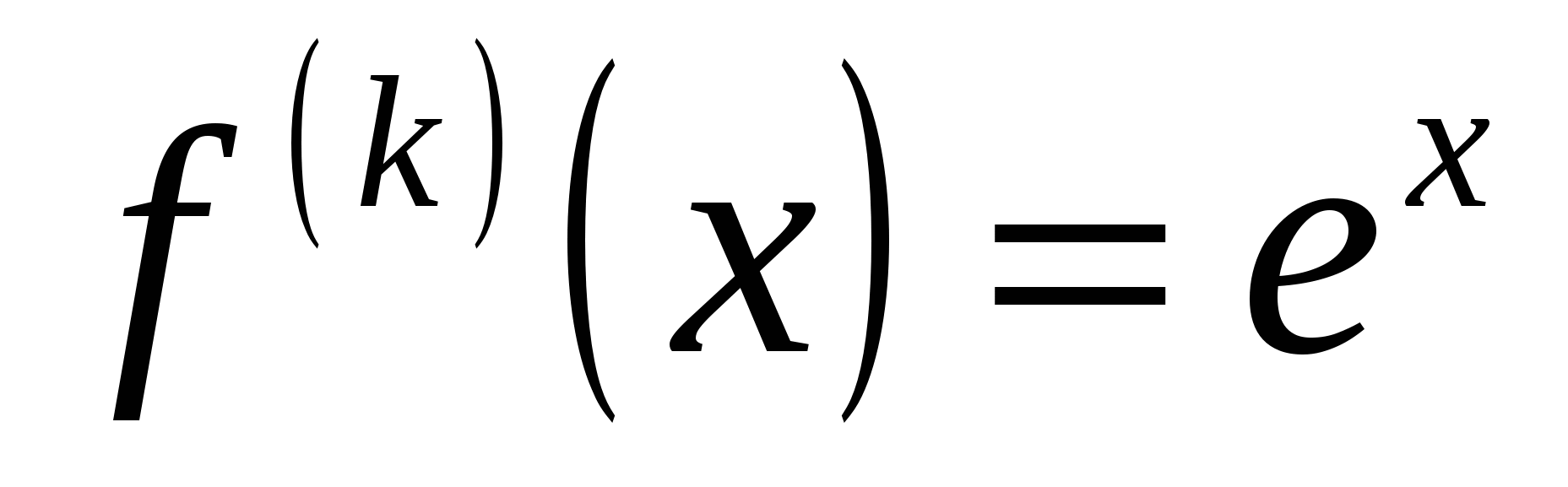 , , 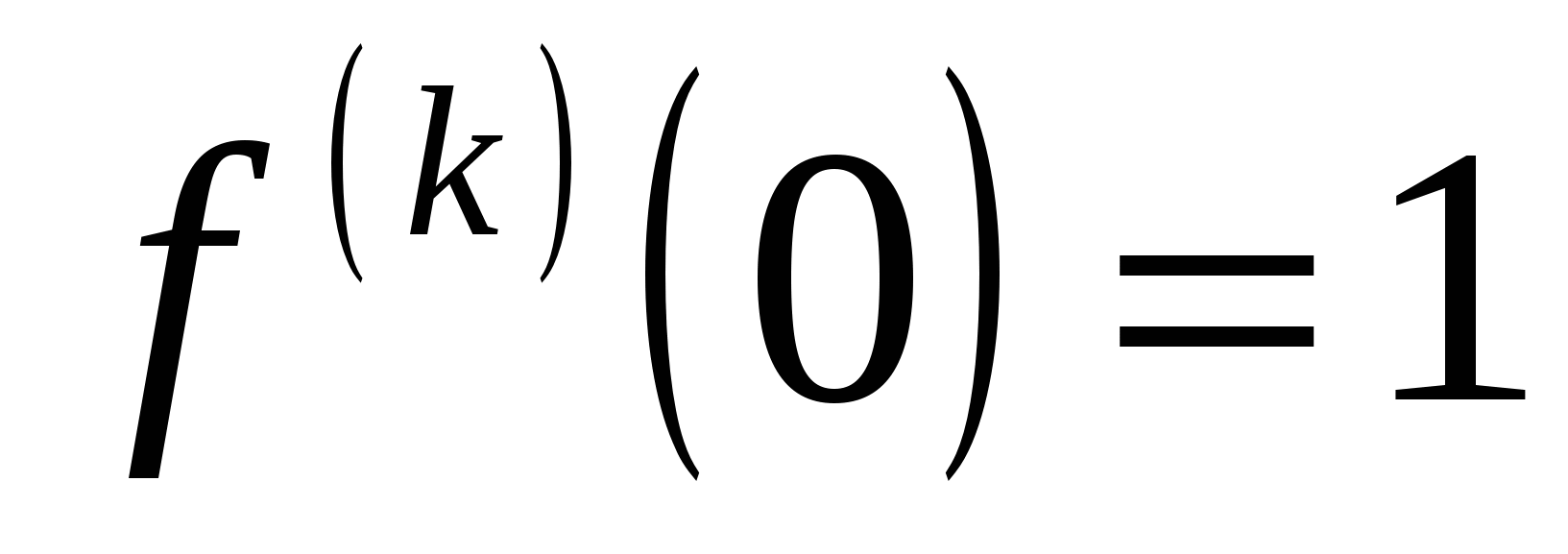 , , 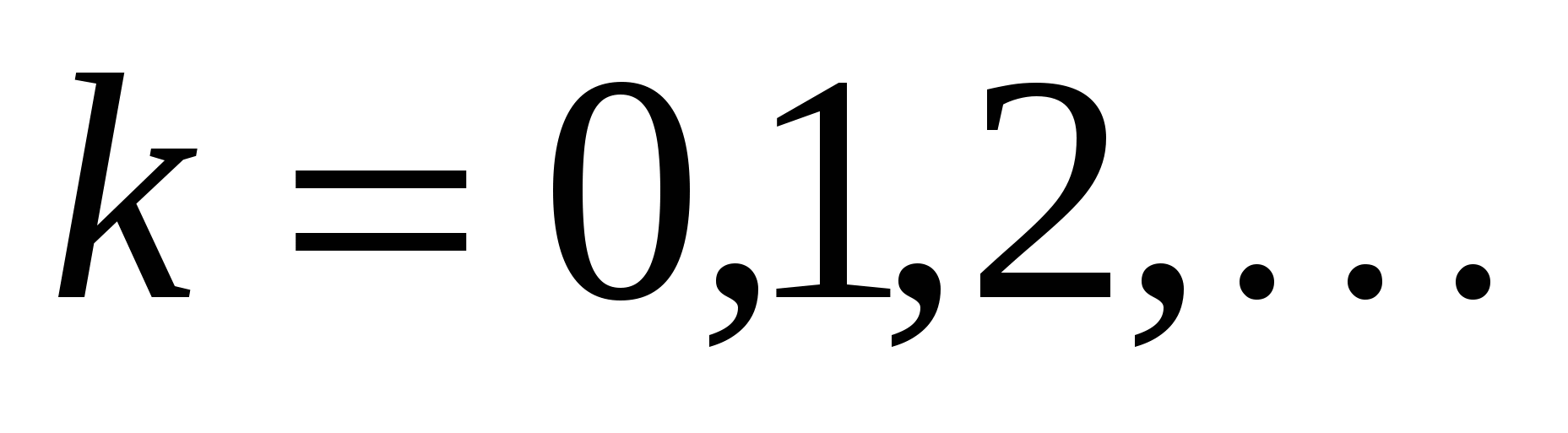 , , 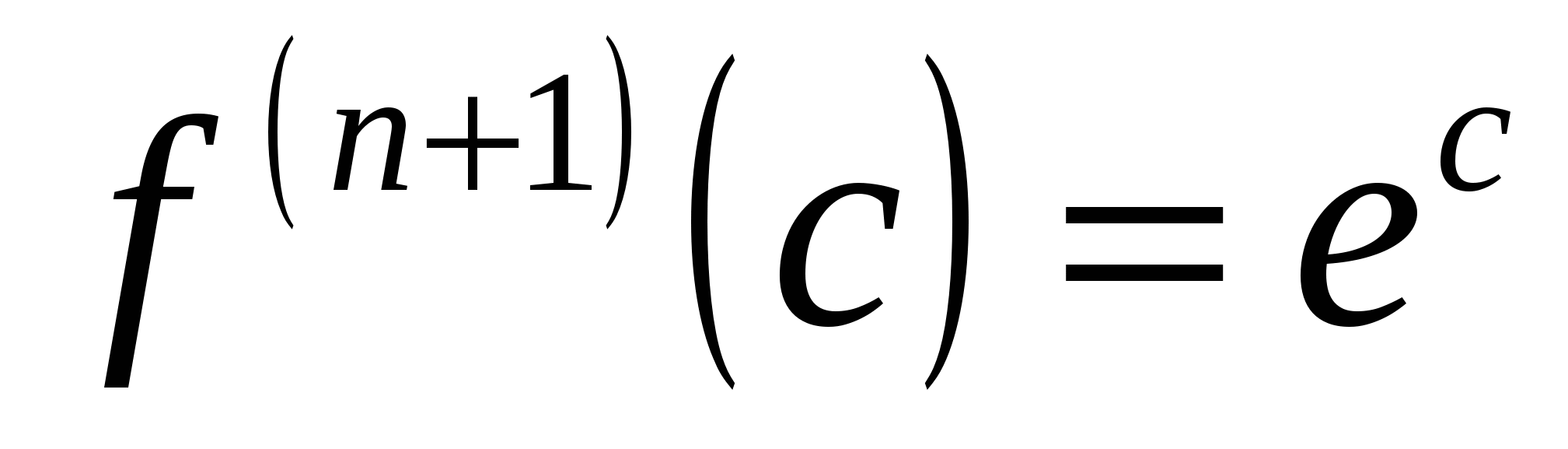 . .
Формула Тейлора с 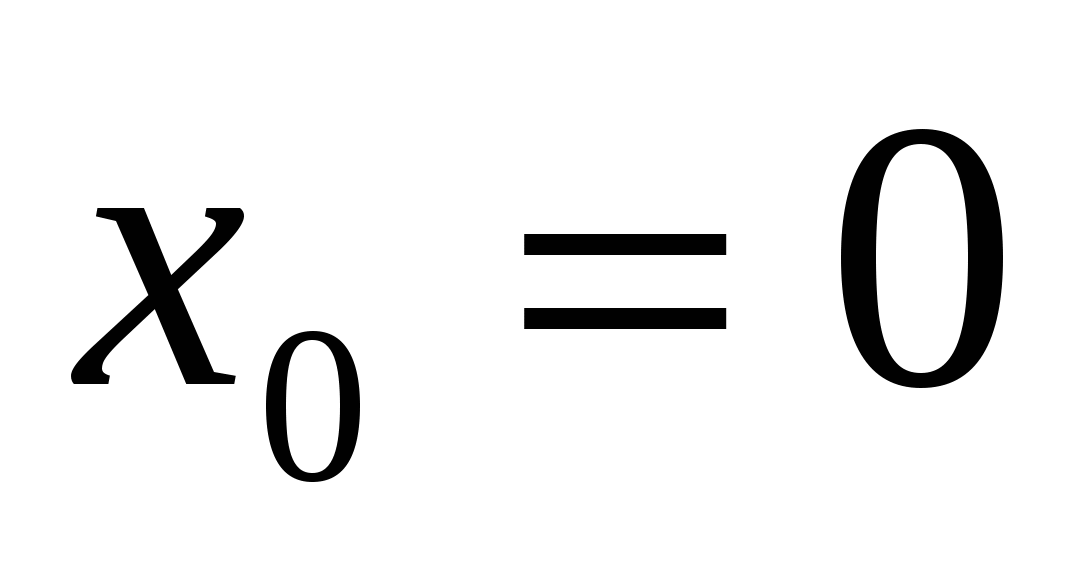 и остаточным членом в форме Лагранжа имеет вид: и остаточным членом в форме Лагранжа имеет вид:
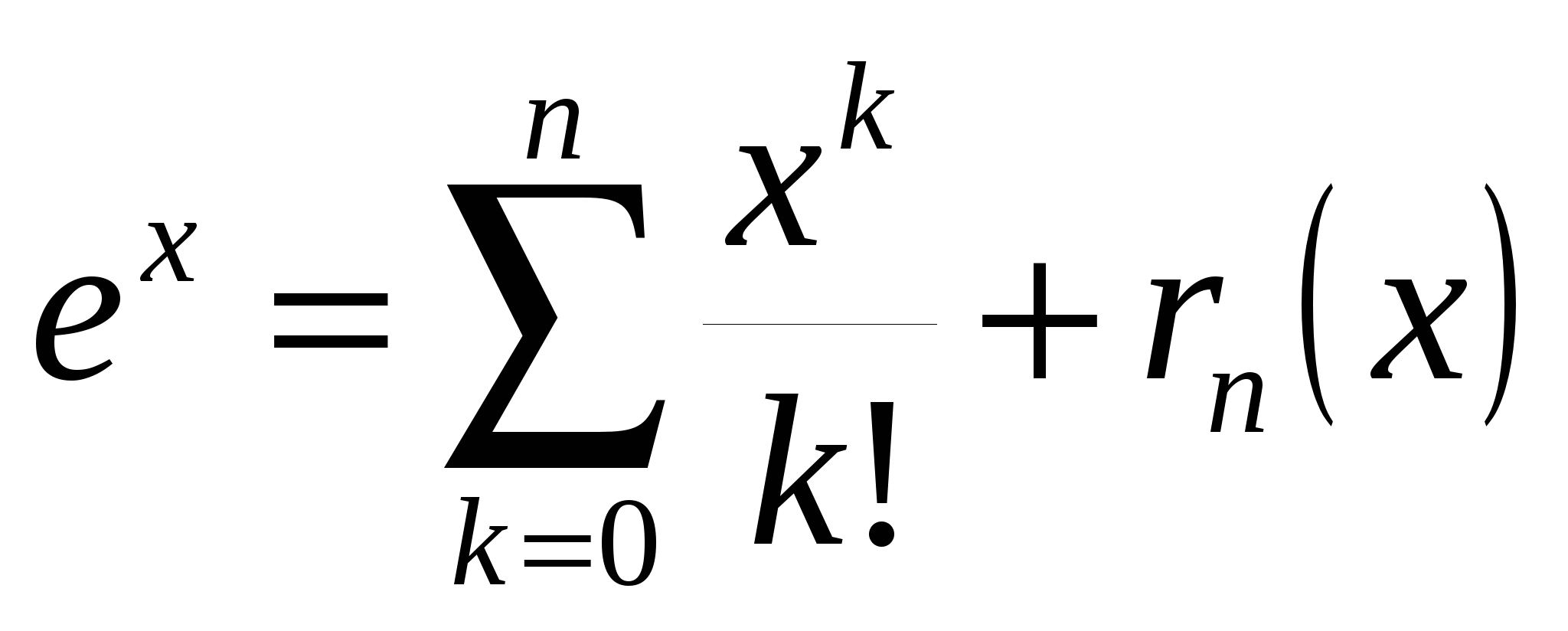 , , 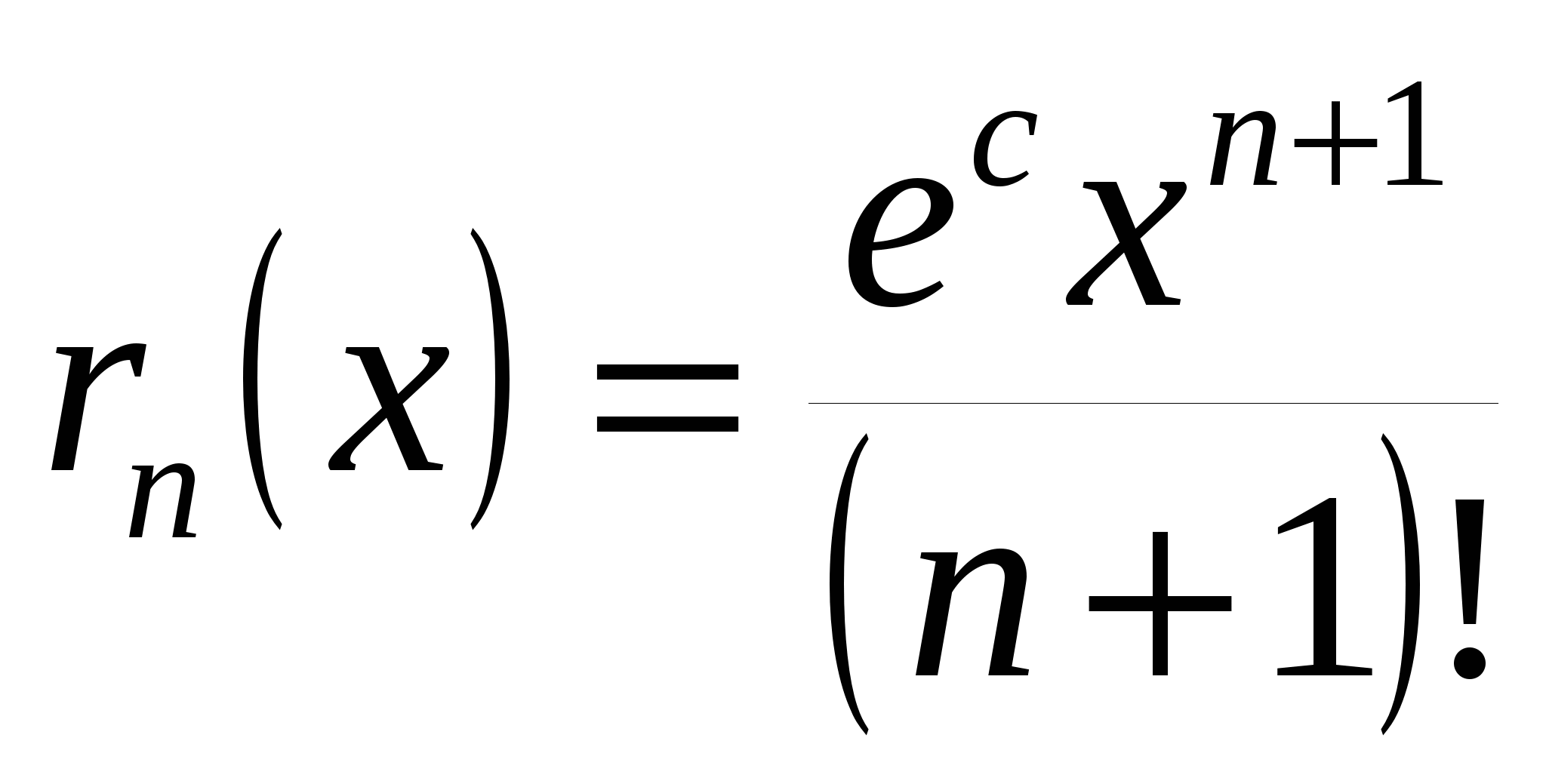 , , 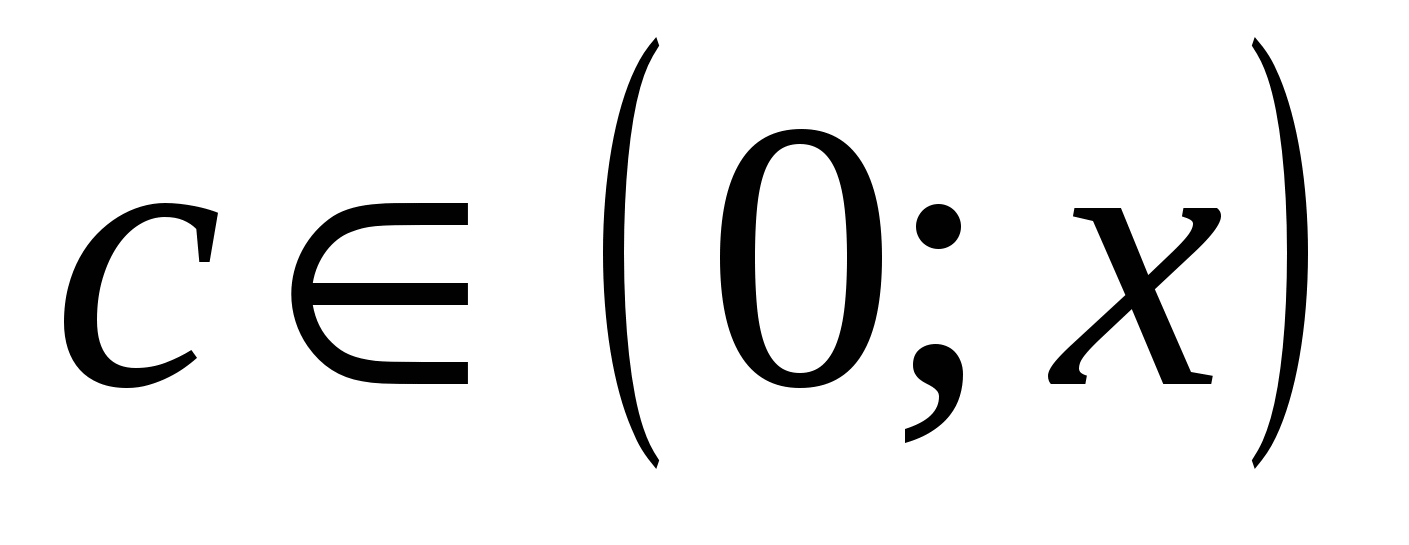 . .
На отрезке 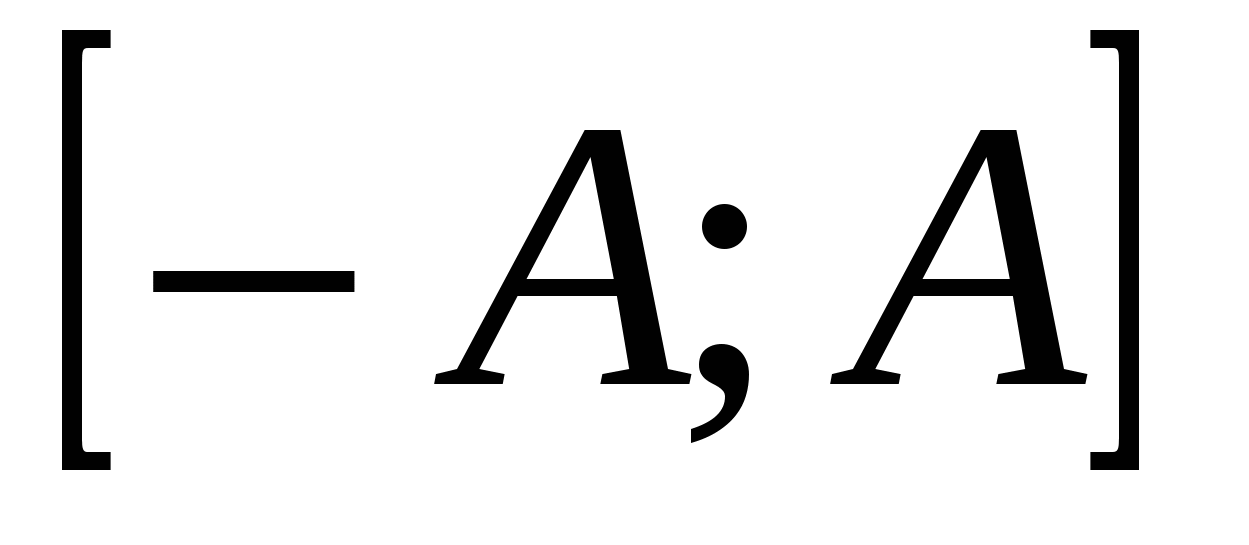 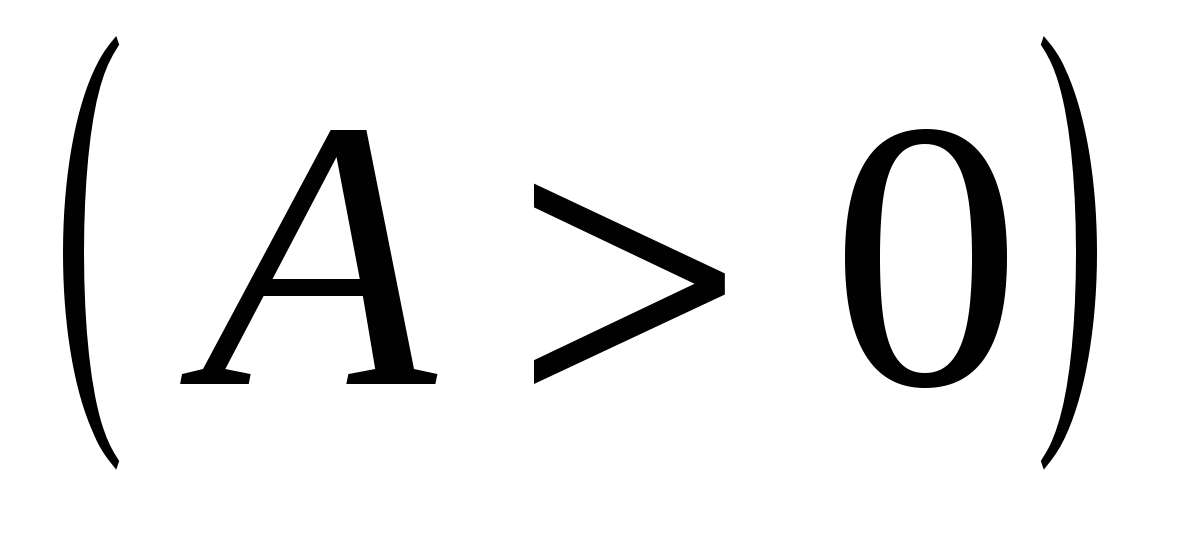
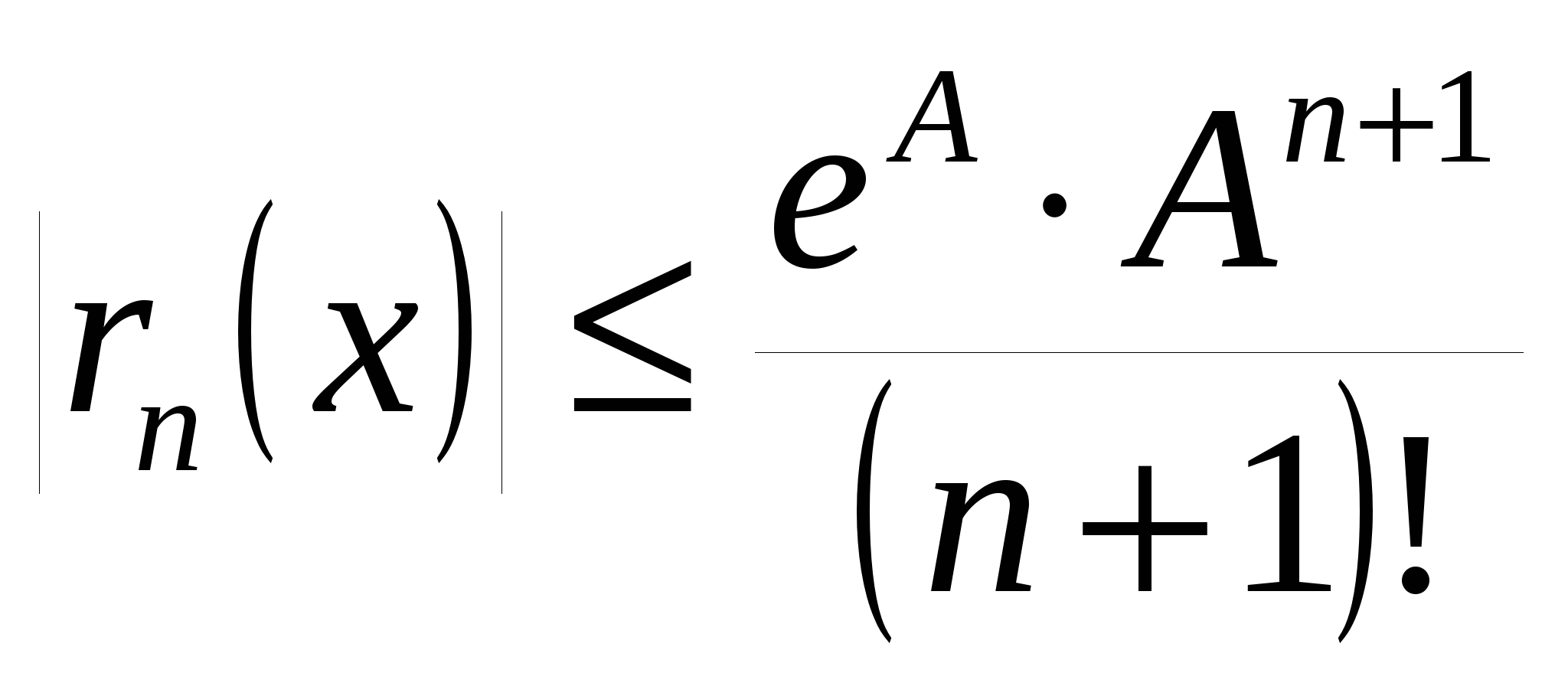 , ,
где 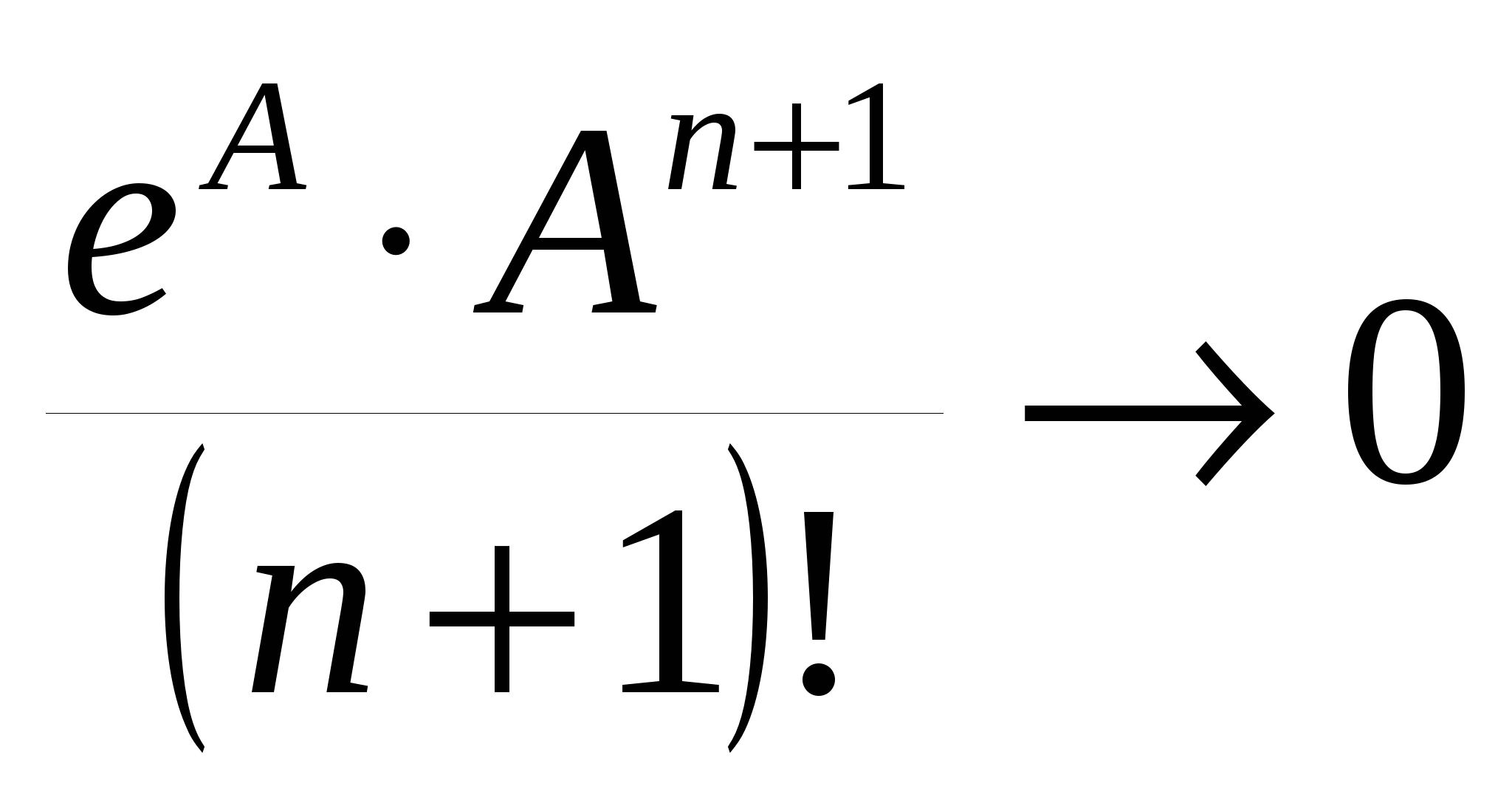 при при  . То есть на . То есть на 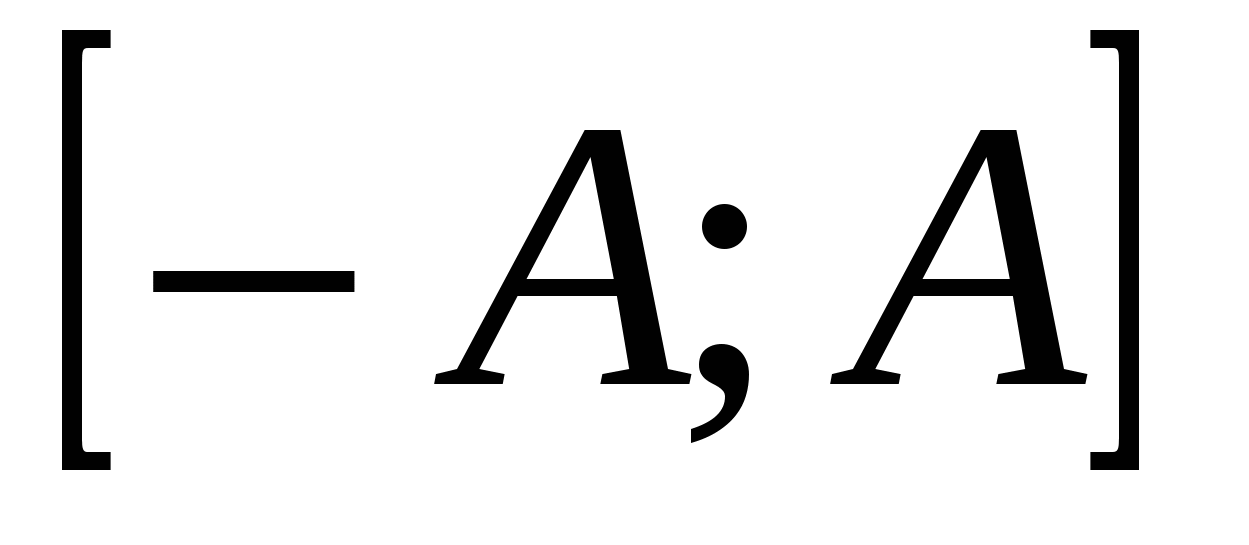 функция функция 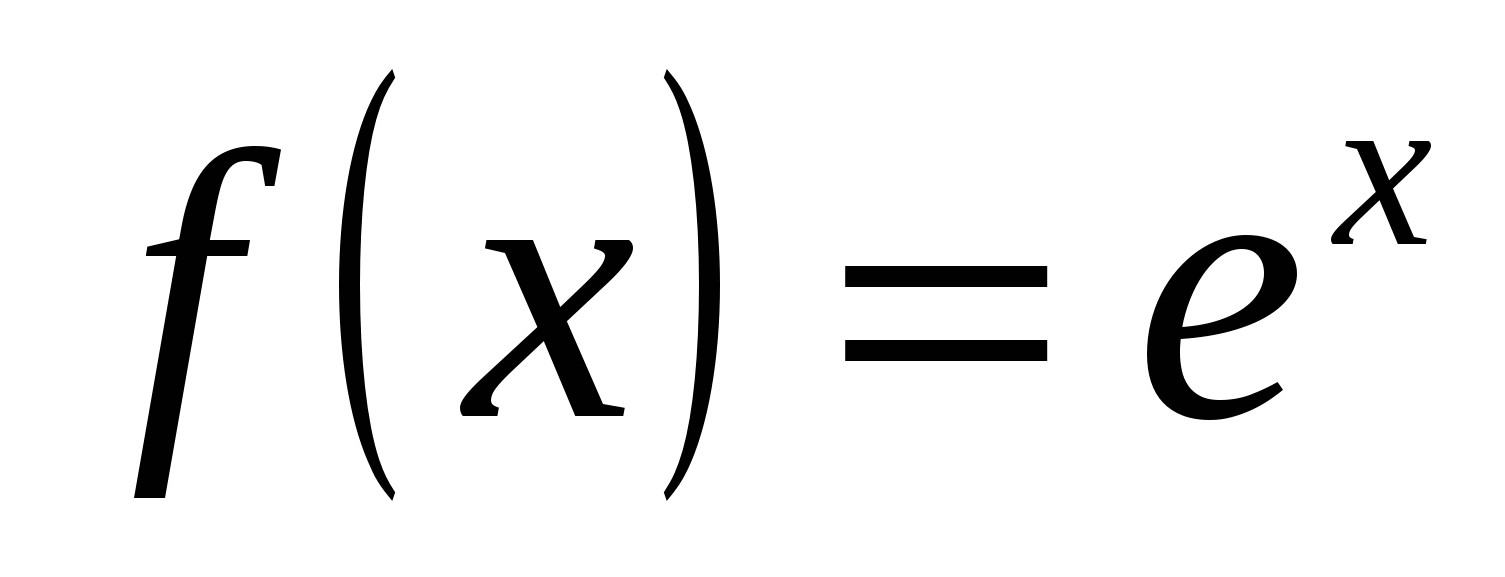 разлагается в ряд Маклорена по степеням x: разлагается в ряд Маклорена по степеням x:
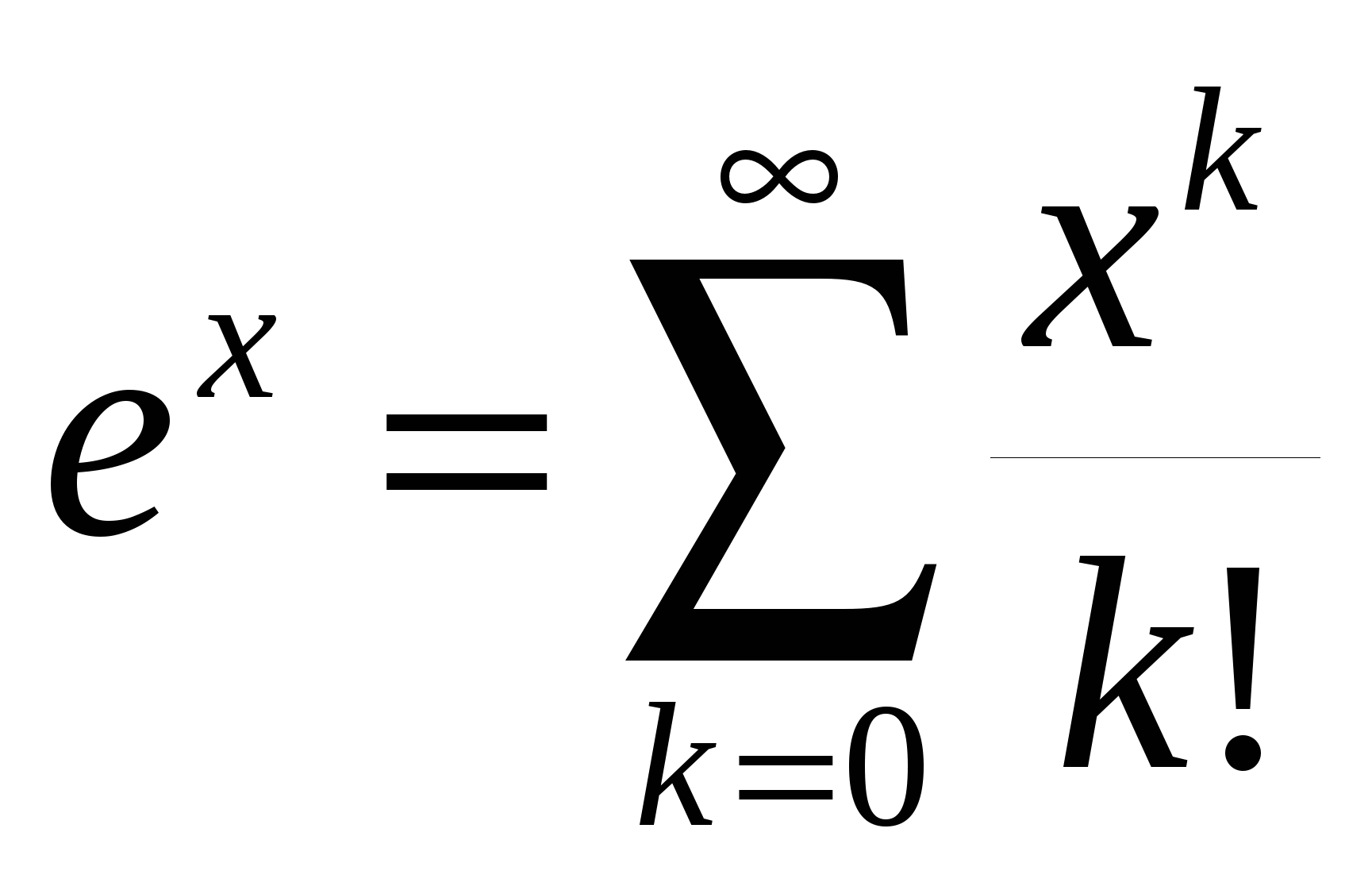 . .
Пример 19.2. Вычислим e с точностью до 0,001:
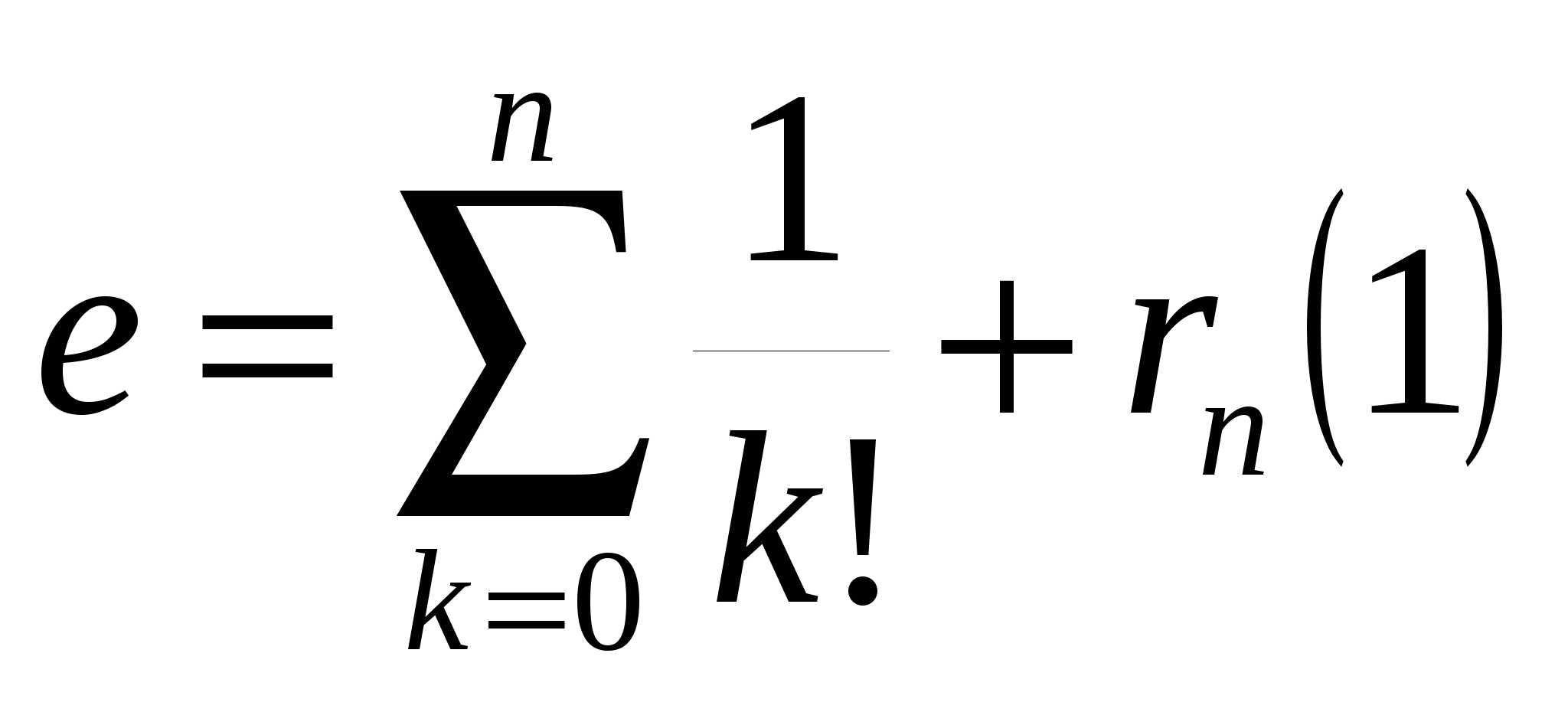 , где , где 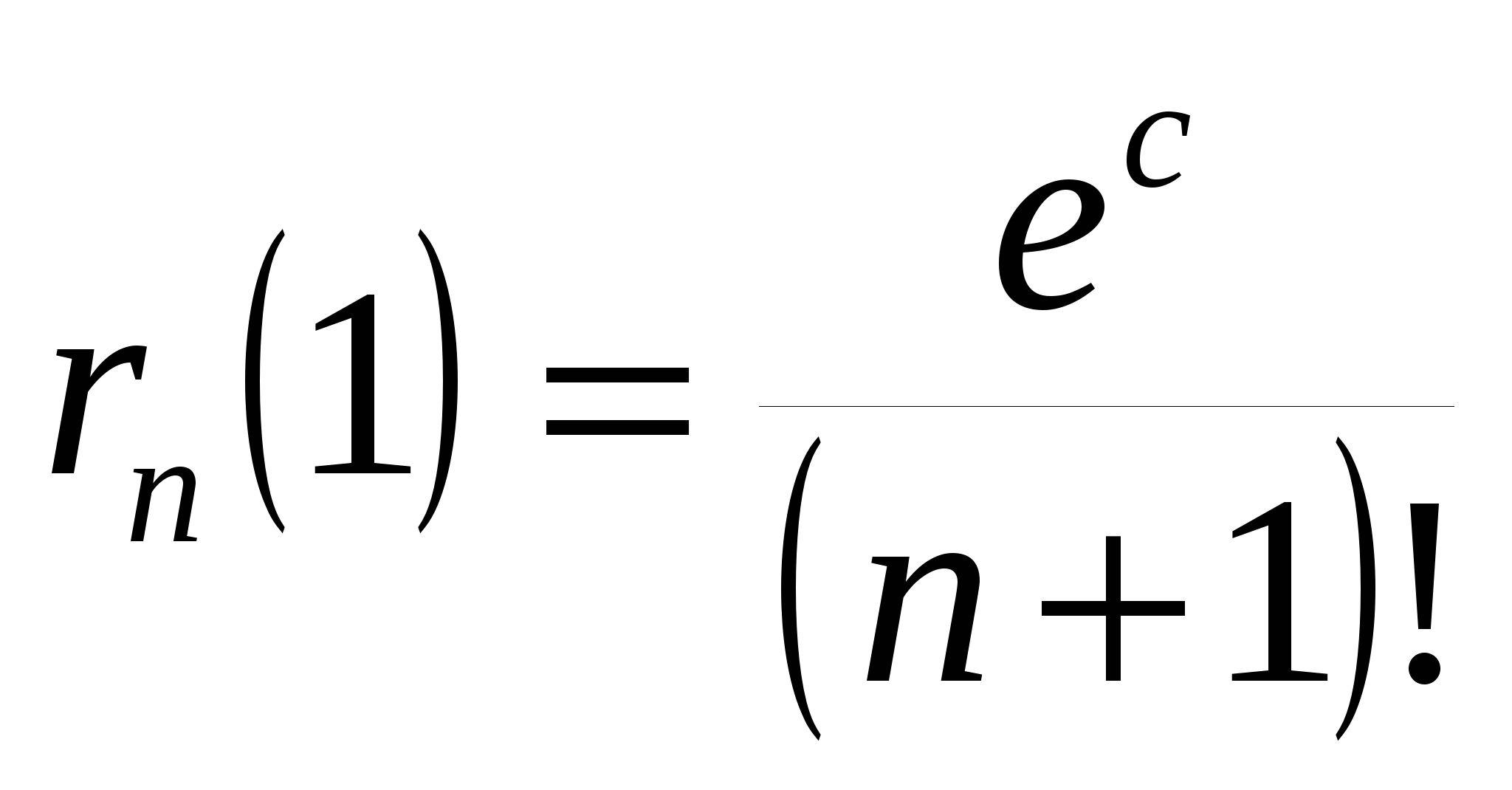 , , 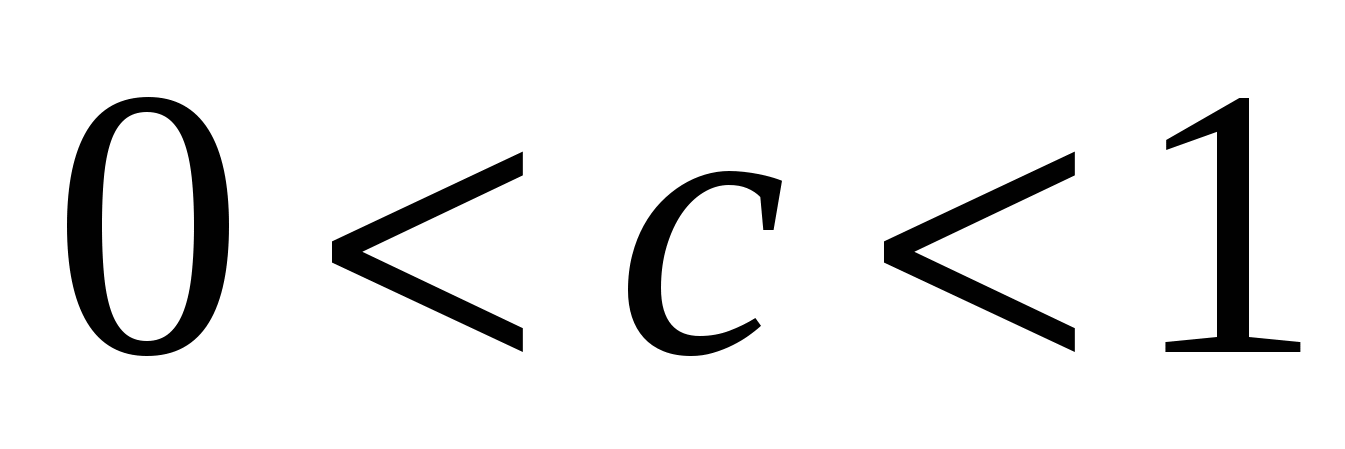 . .
Надо подобрать n настолько большим, чтобы 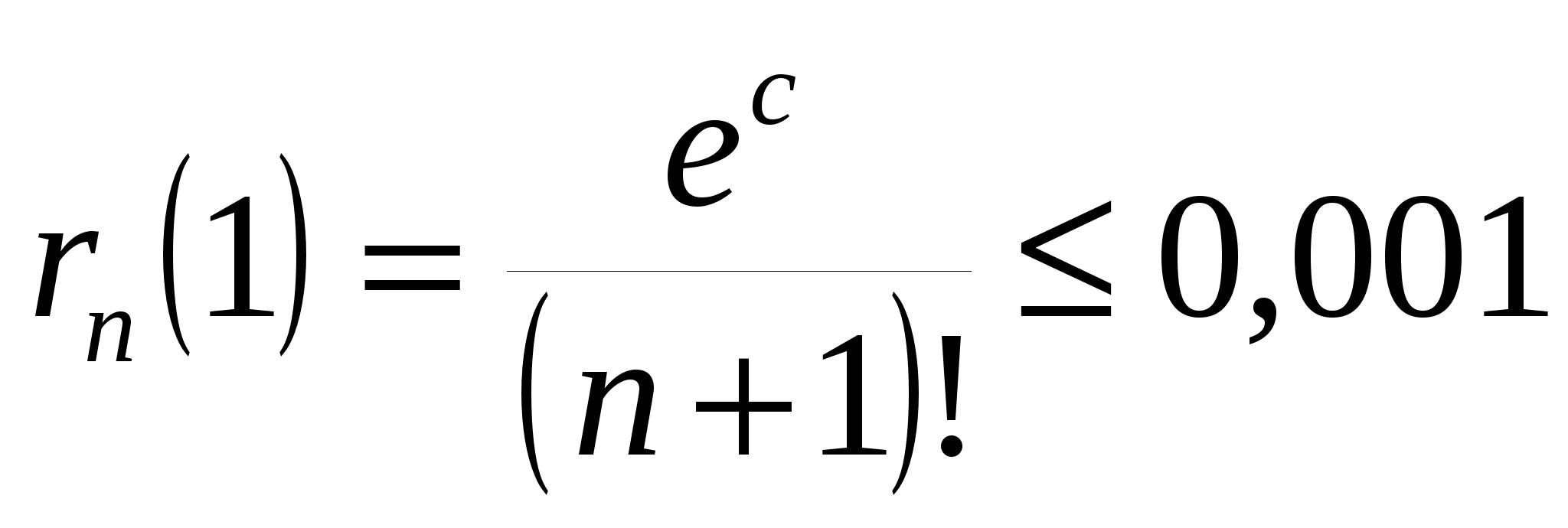 . Так как . Так как 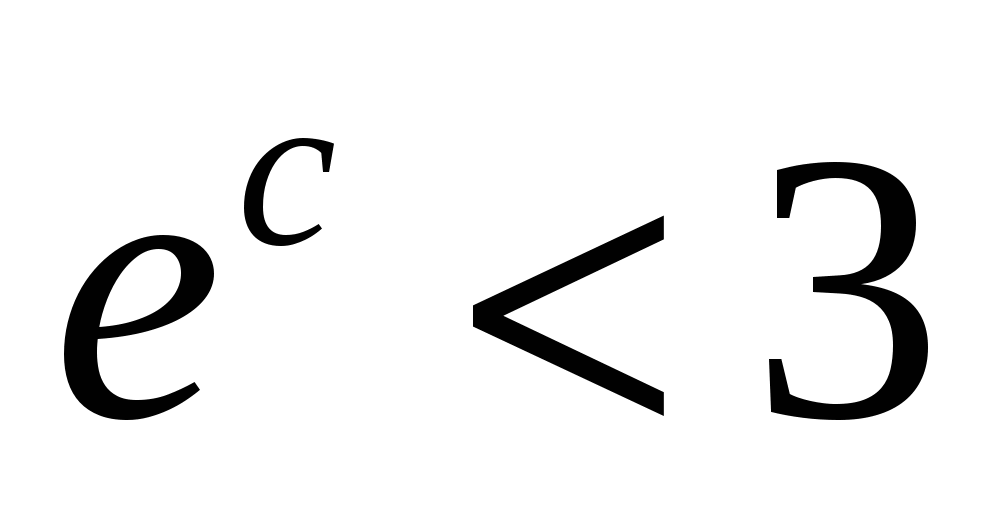 , решим неравенство , решим неравенство 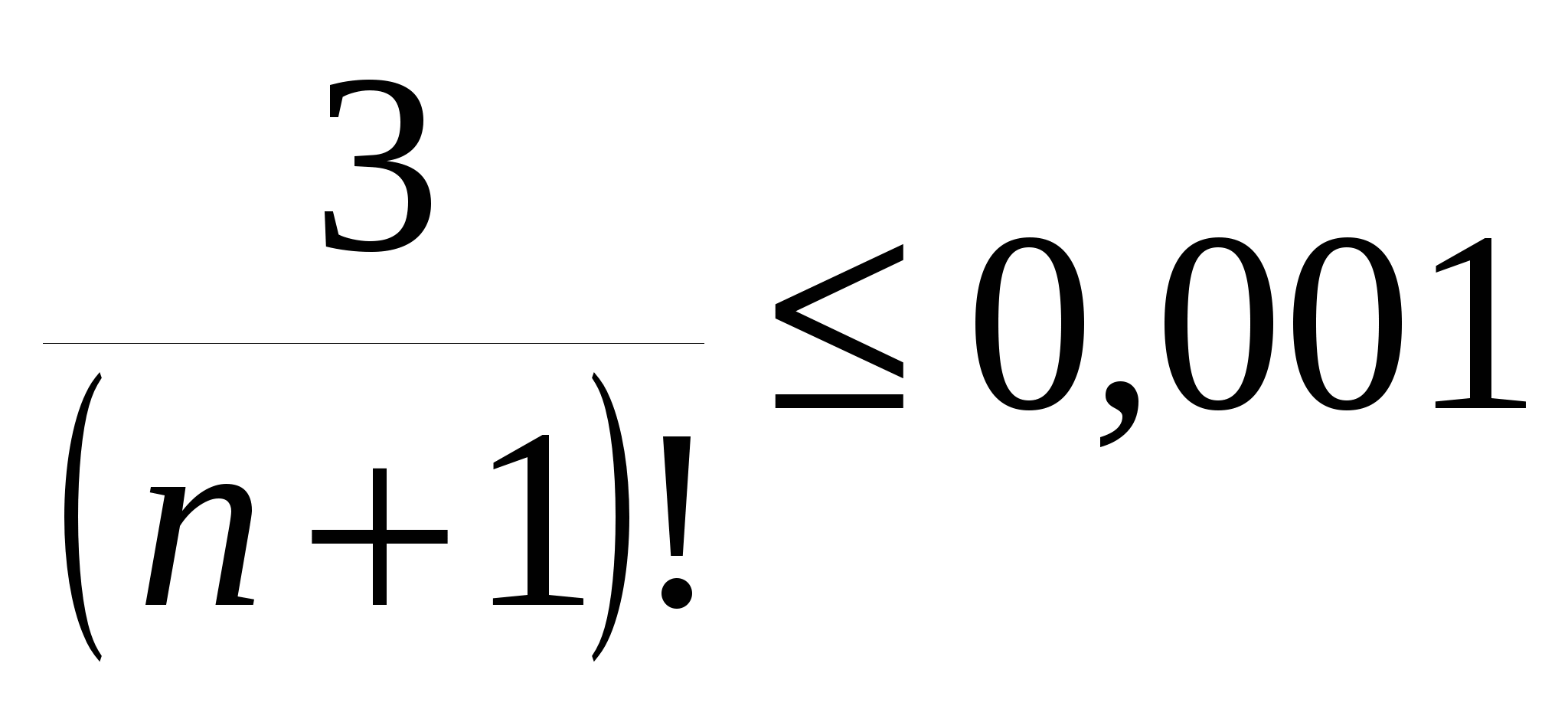 . Оно начинает выполняться при . Оно начинает выполняться при 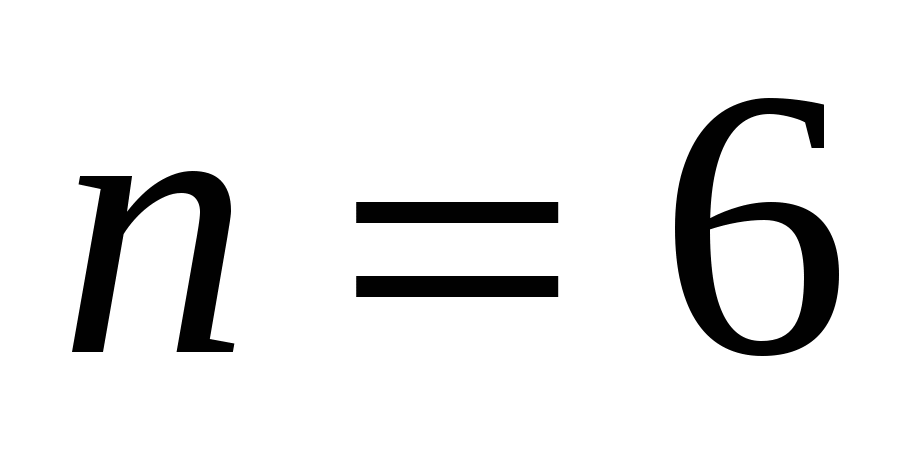 . Следовательно, . Следовательно,
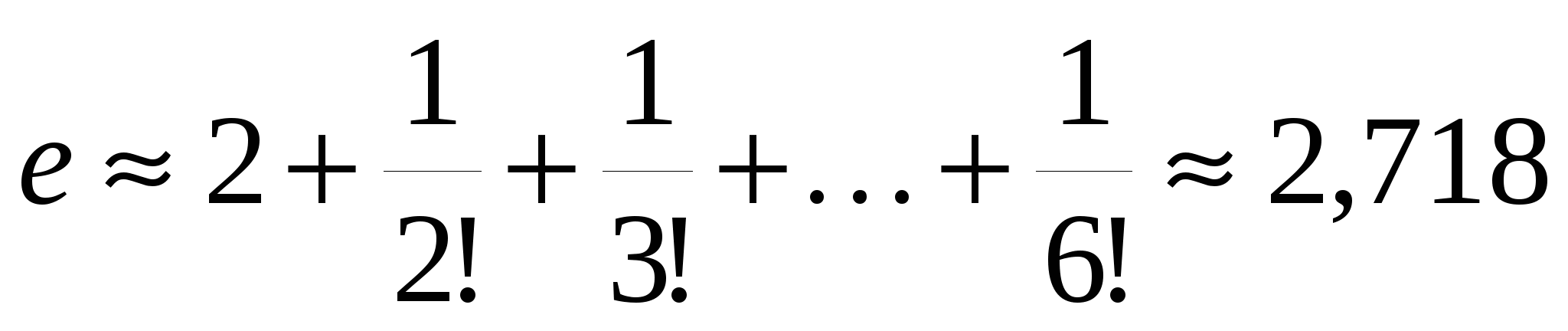 . .
2)  . Данная функция имеет производную любого порядка и . Данная функция имеет производную любого порядка и
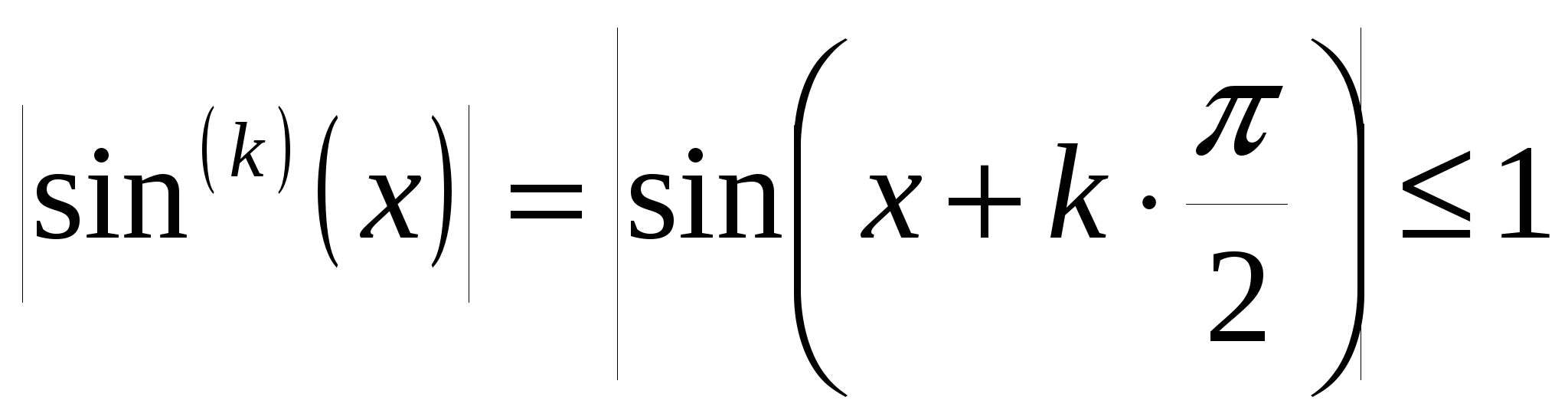 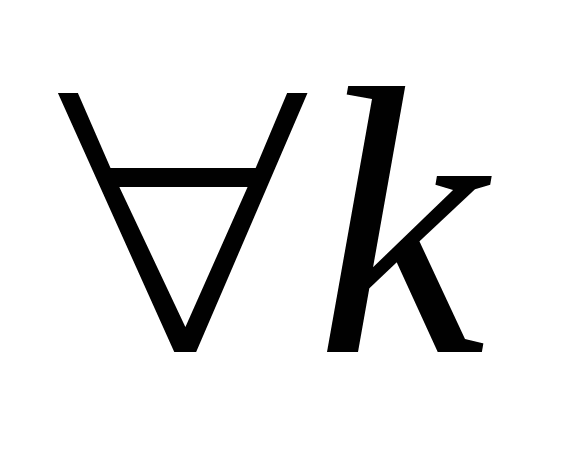 . .
Надо учесть, что 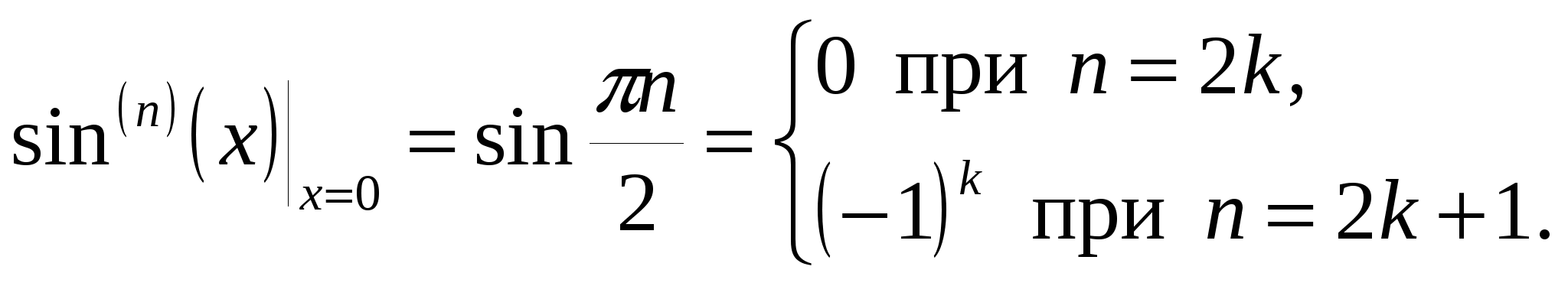
Функция  разлагается в сходящийся к ней на разлагается в сходящийся к ней на 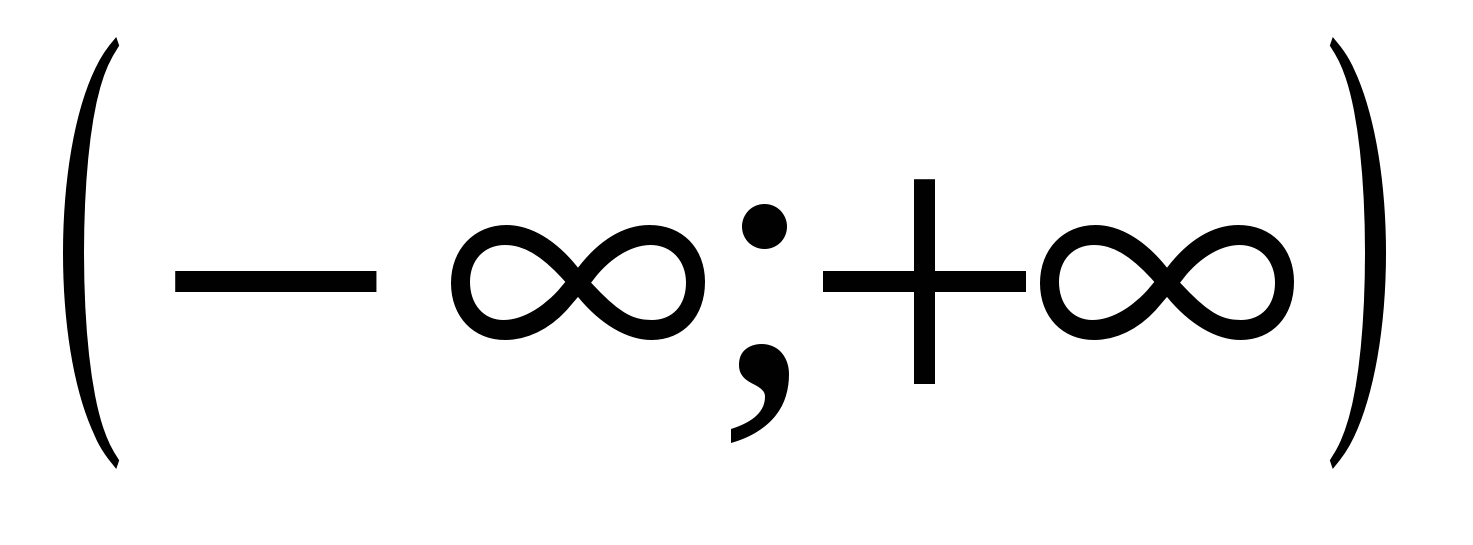 ряд Тейлора по степеням x: ряд Тейлора по степеням x:
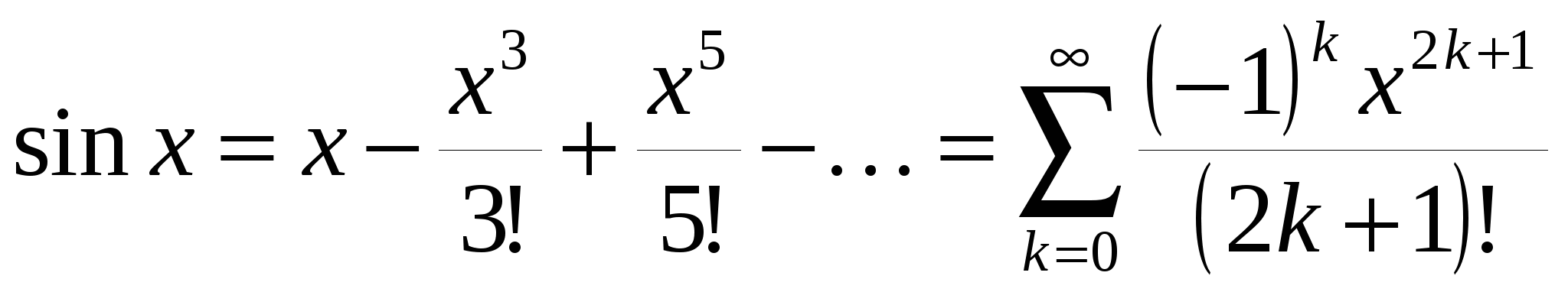 . .
Формула Тейлора функции  по степеням x имеет вид: по степеням x имеет вид:
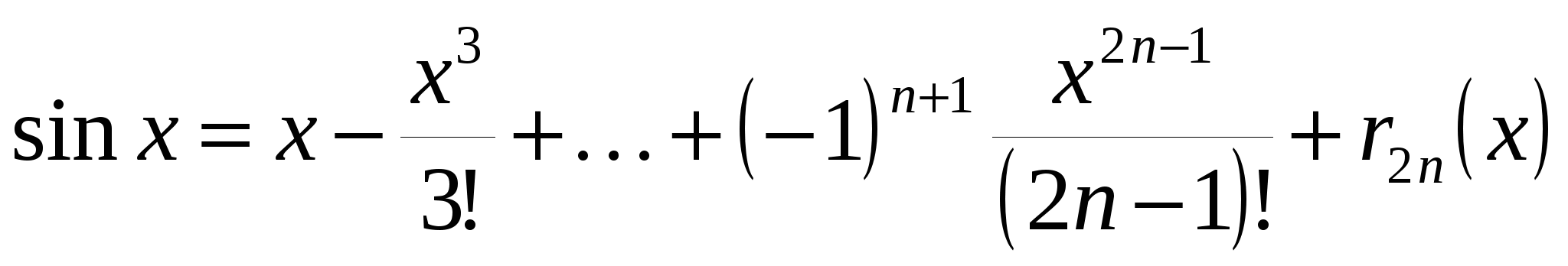 , ,
где
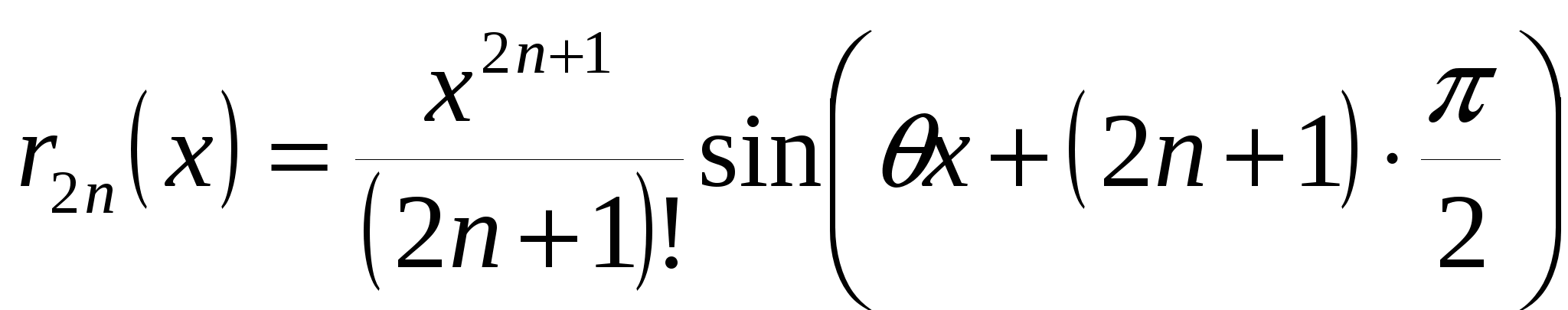 , , 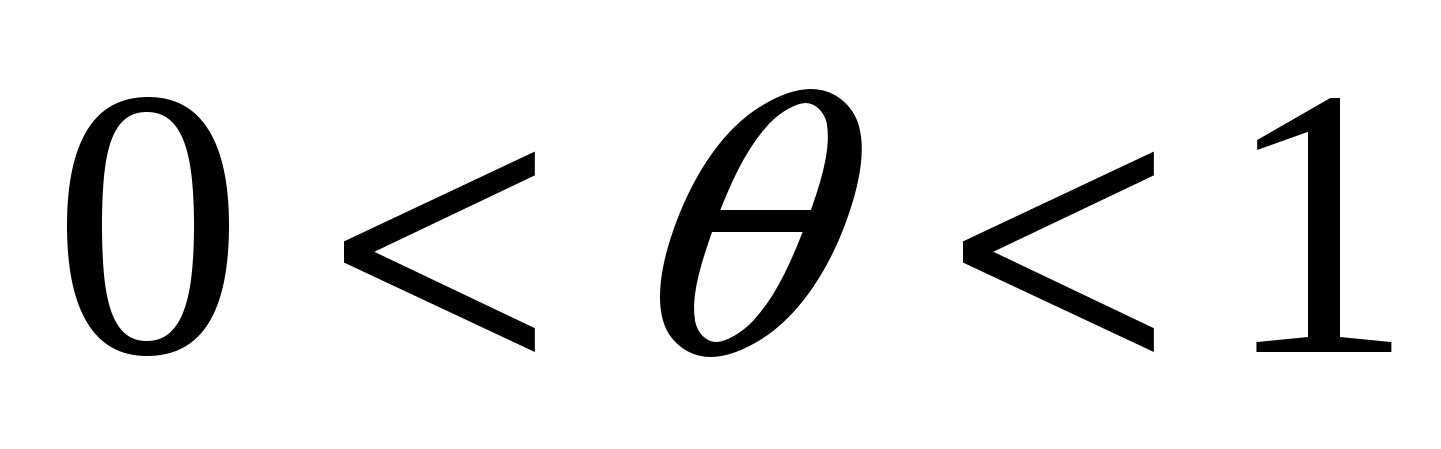 . .
Отсюда следует, что 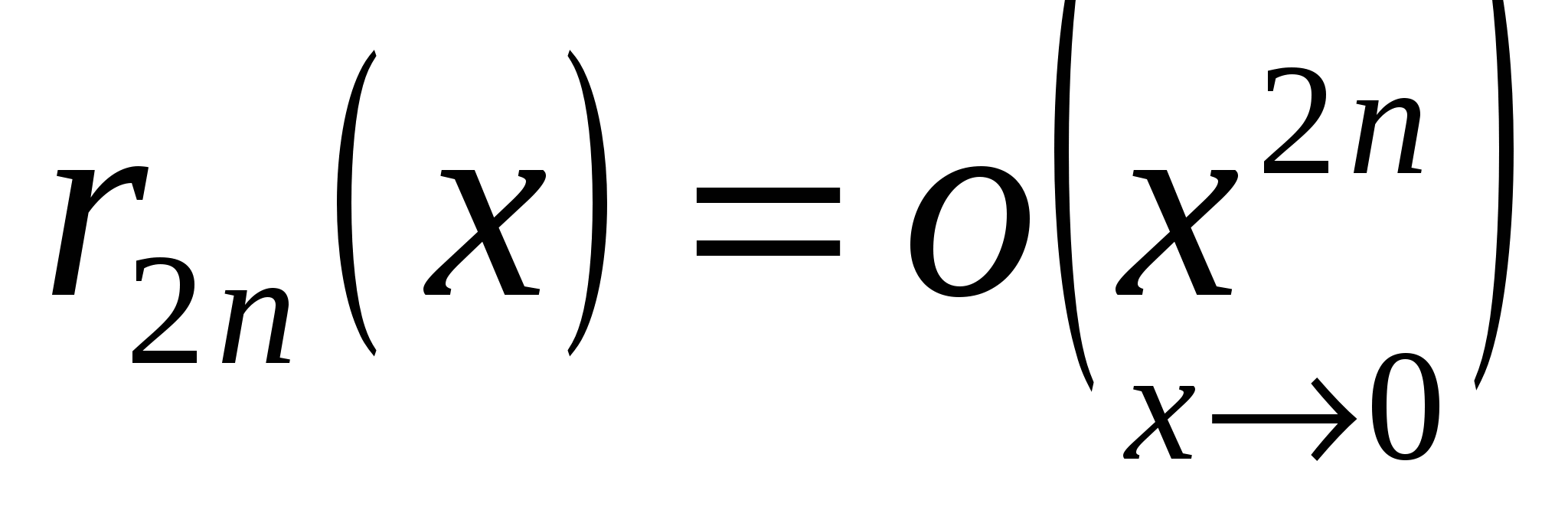 и и
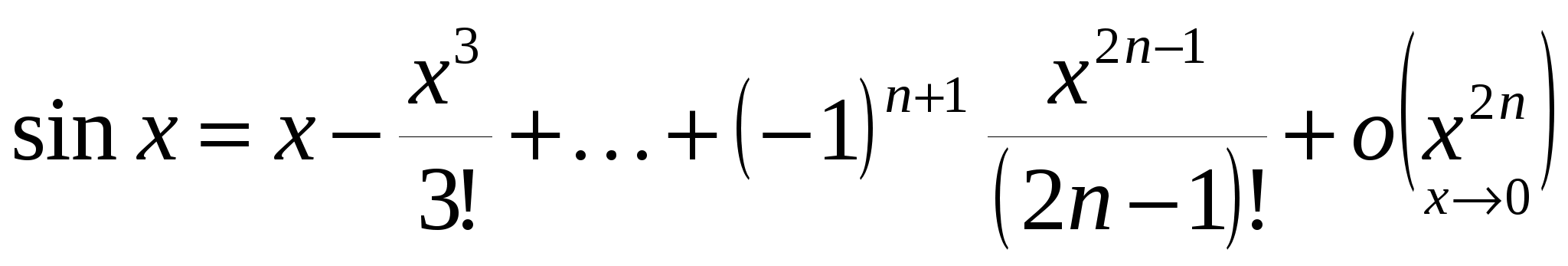 . .
Пример 19.3. Вычислим 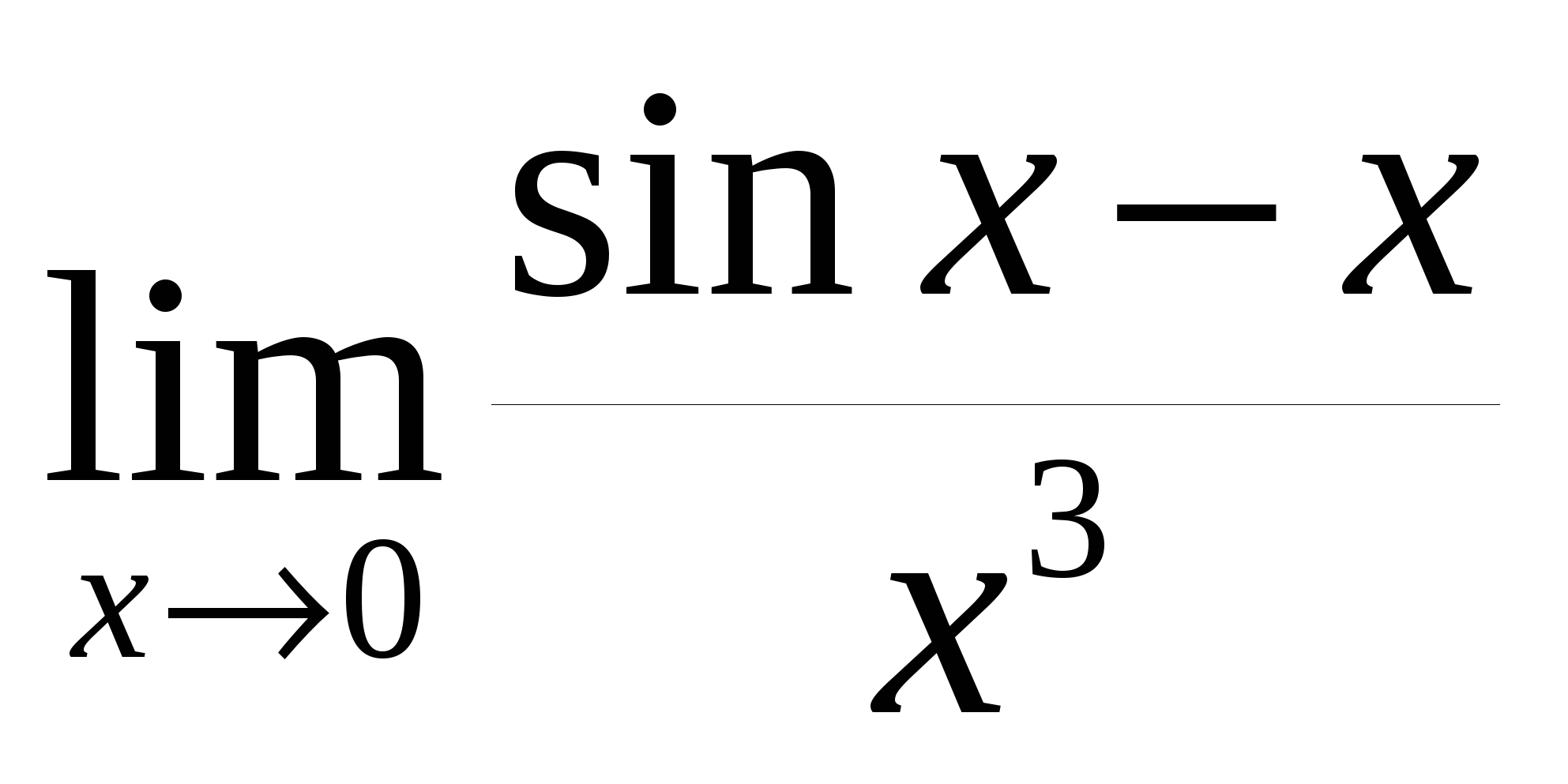 . .
Ряд Тейлора для синуса 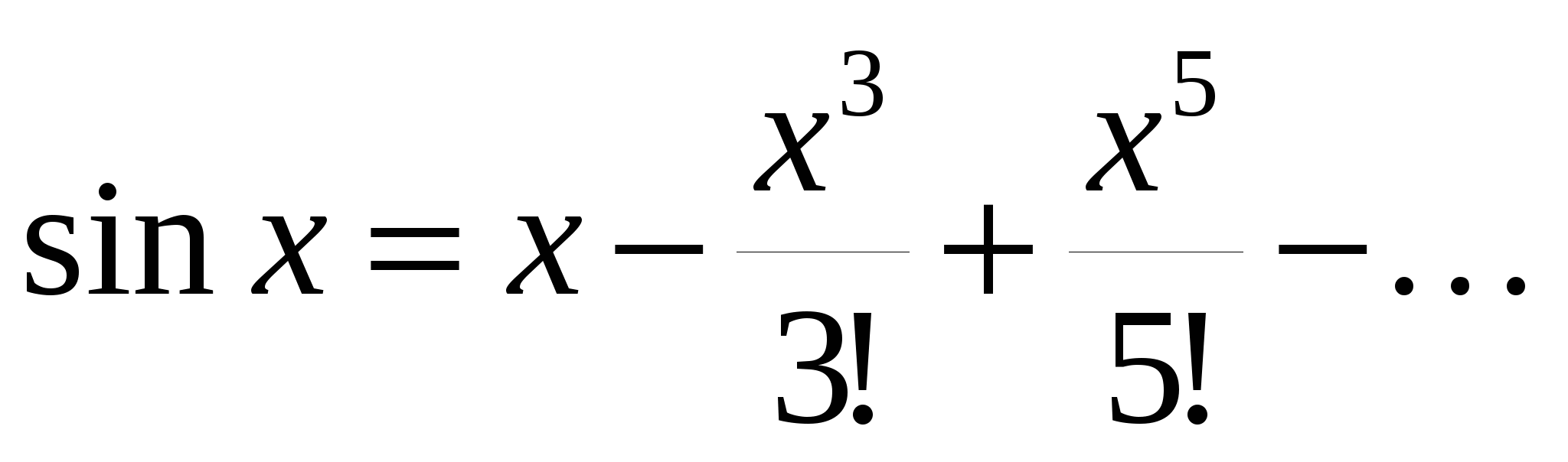 . Поэтому . Поэтому
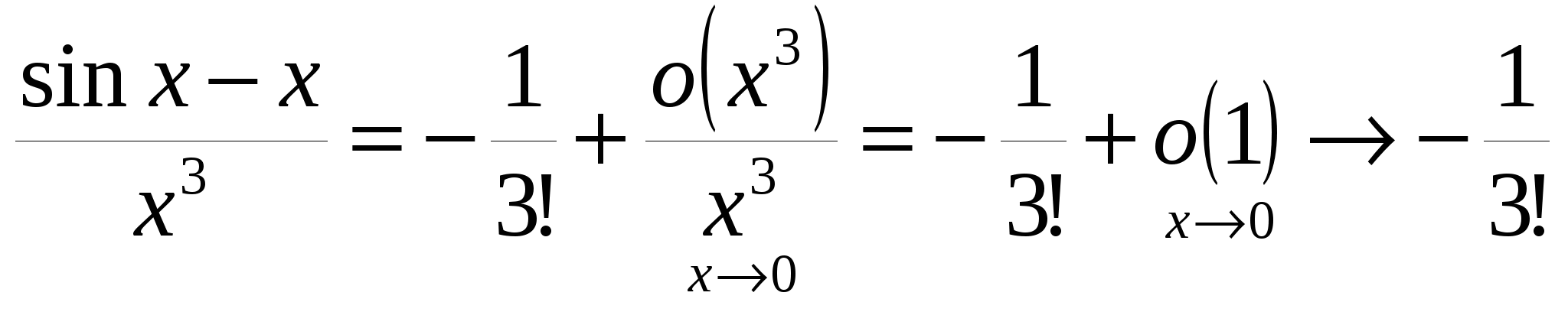 , ,
то есть 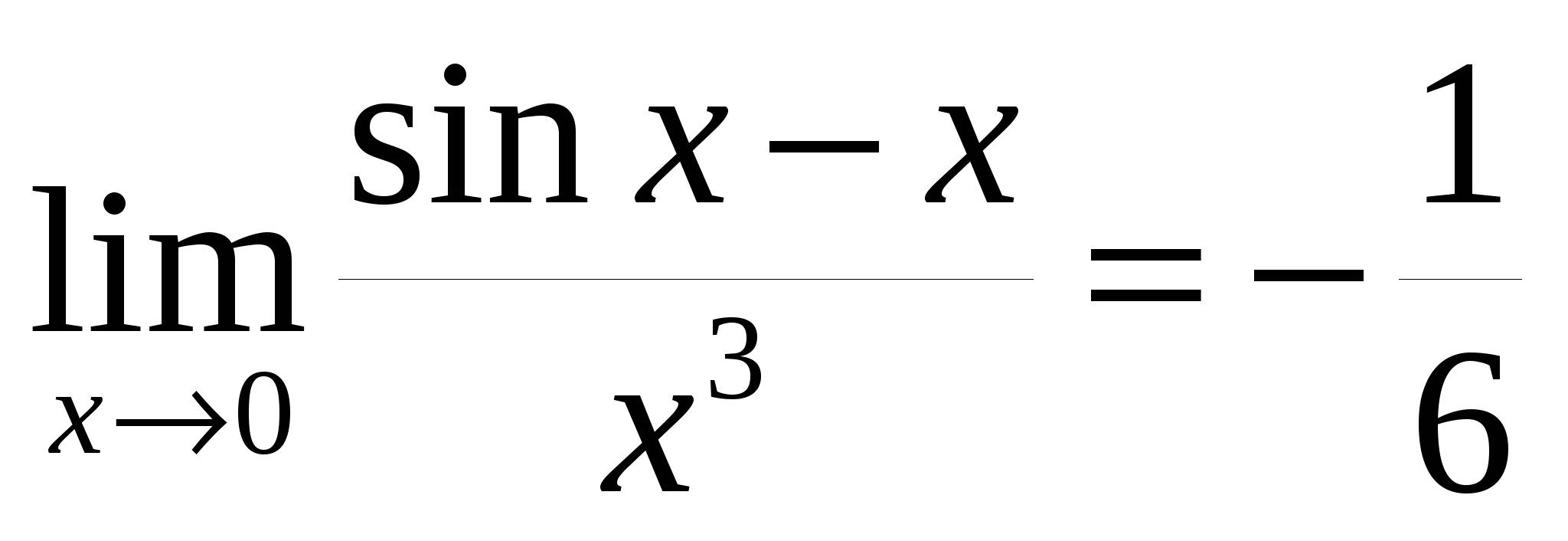 . .
На самом деле остаток имеет вид 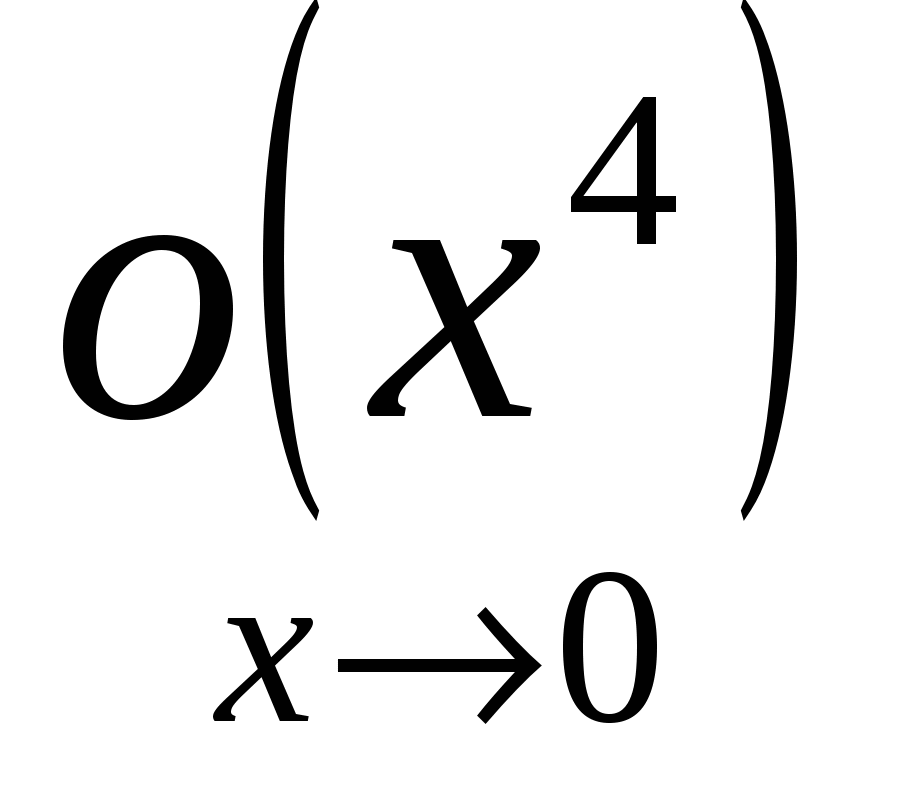 , но для наших целей достаточно , но для наших целей достаточно 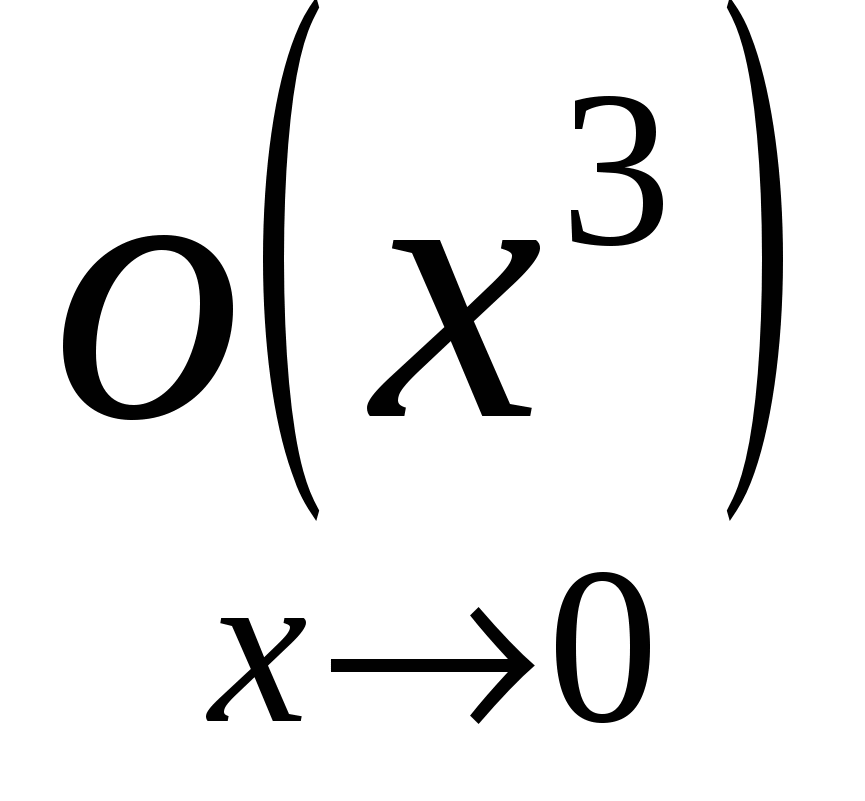 . Надо иметь в виду, что если некоторая функция от x есть . Надо иметь в виду, что если некоторая функция от x есть 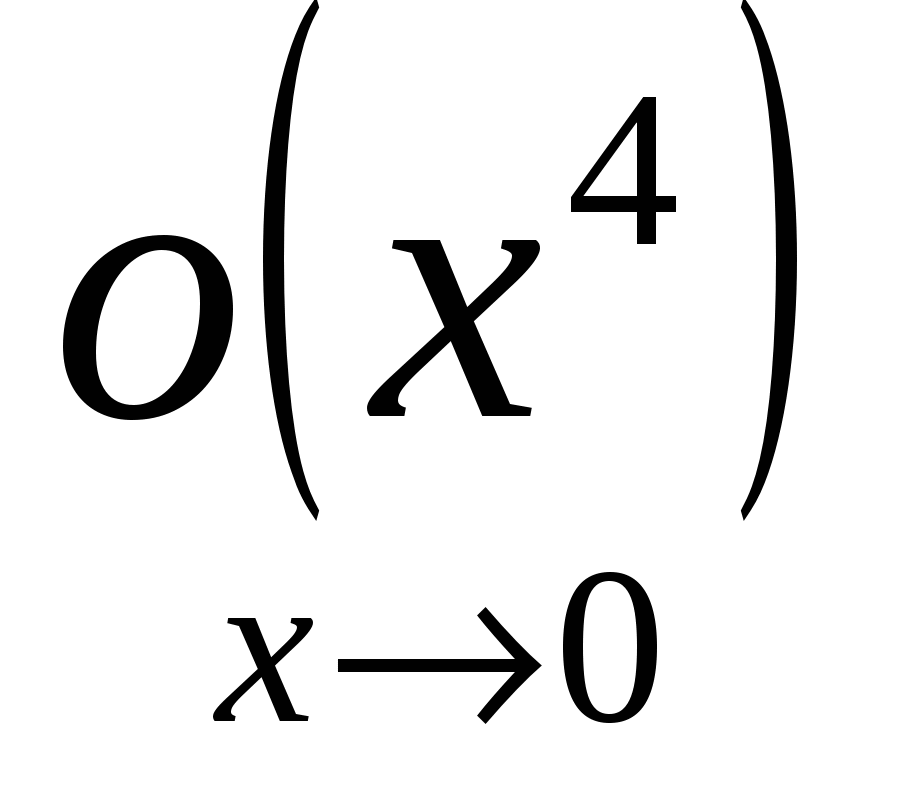 , то она есть также , то она есть также 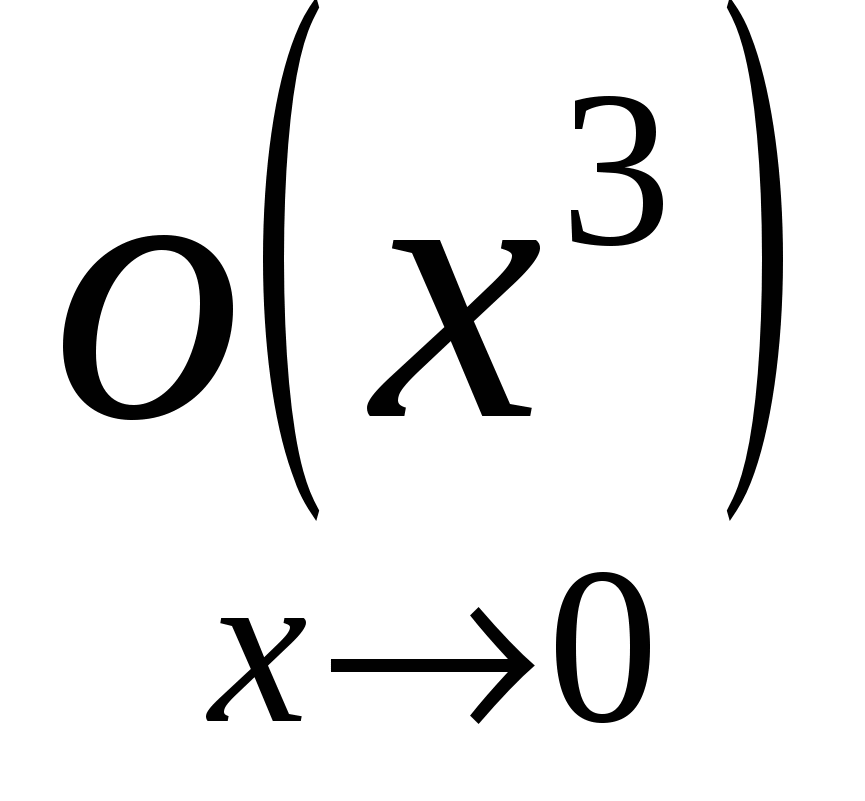 (но вообще не наоборот). (но вообще не наоборот).
3) 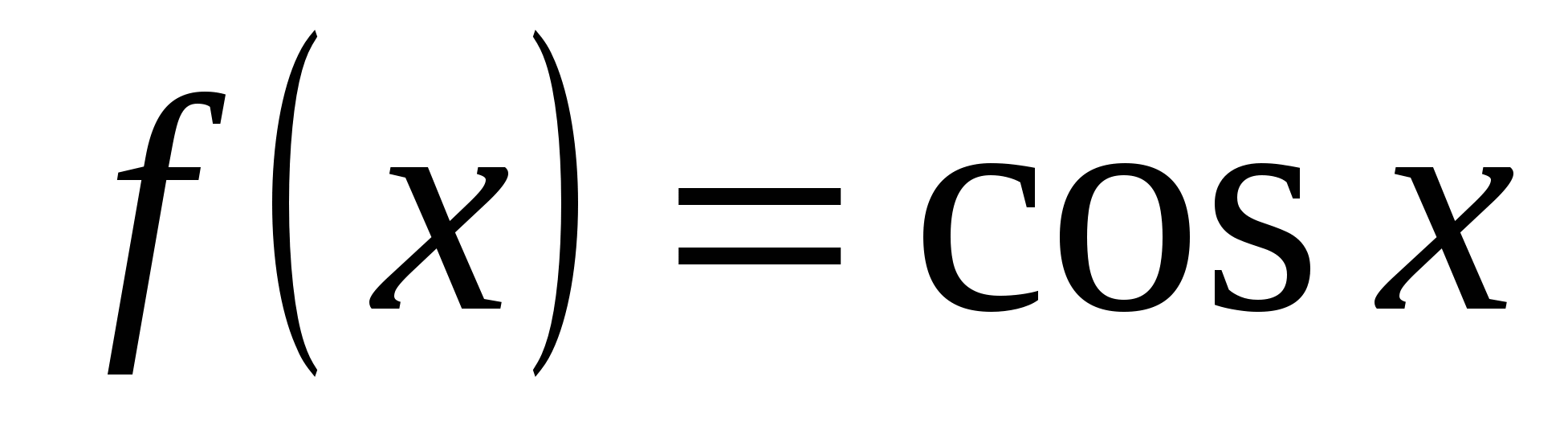 . Аналогично можно получить, что . Аналогично можно получить, что
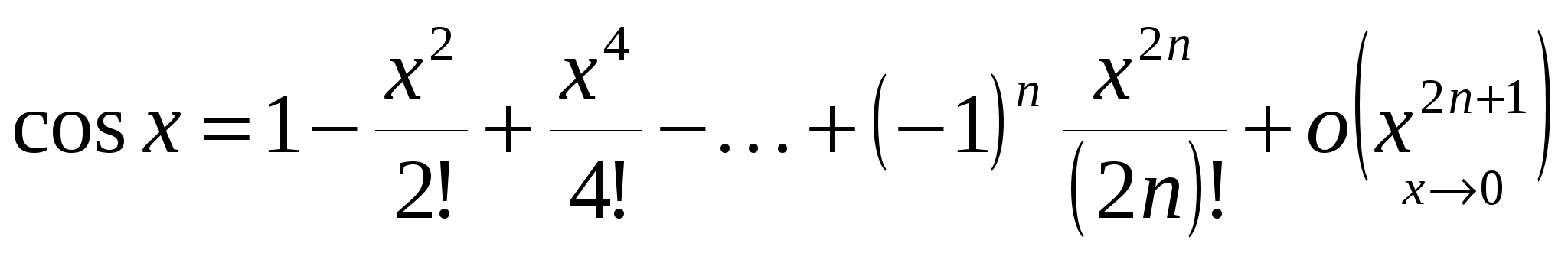 . .
Пример 19.4. 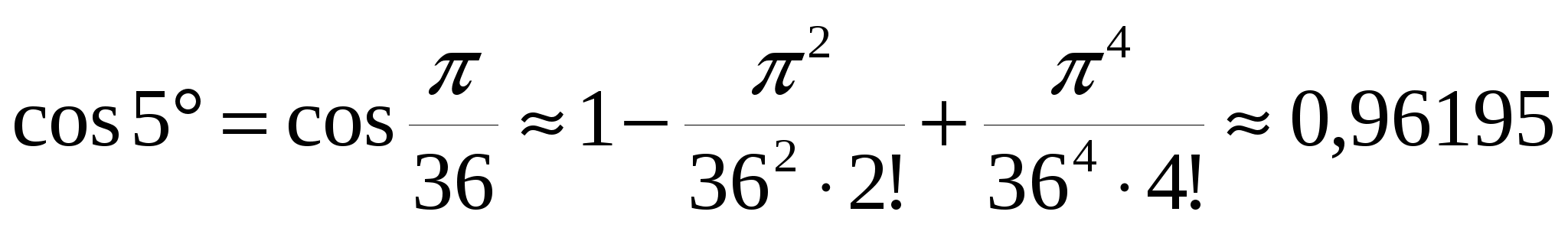 (с точностью до (с точностью до 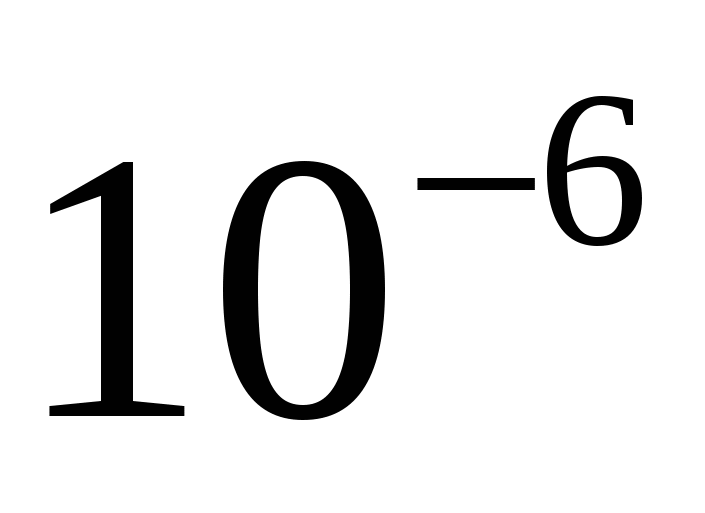 ). ).
Пример 19.5. Вычислим 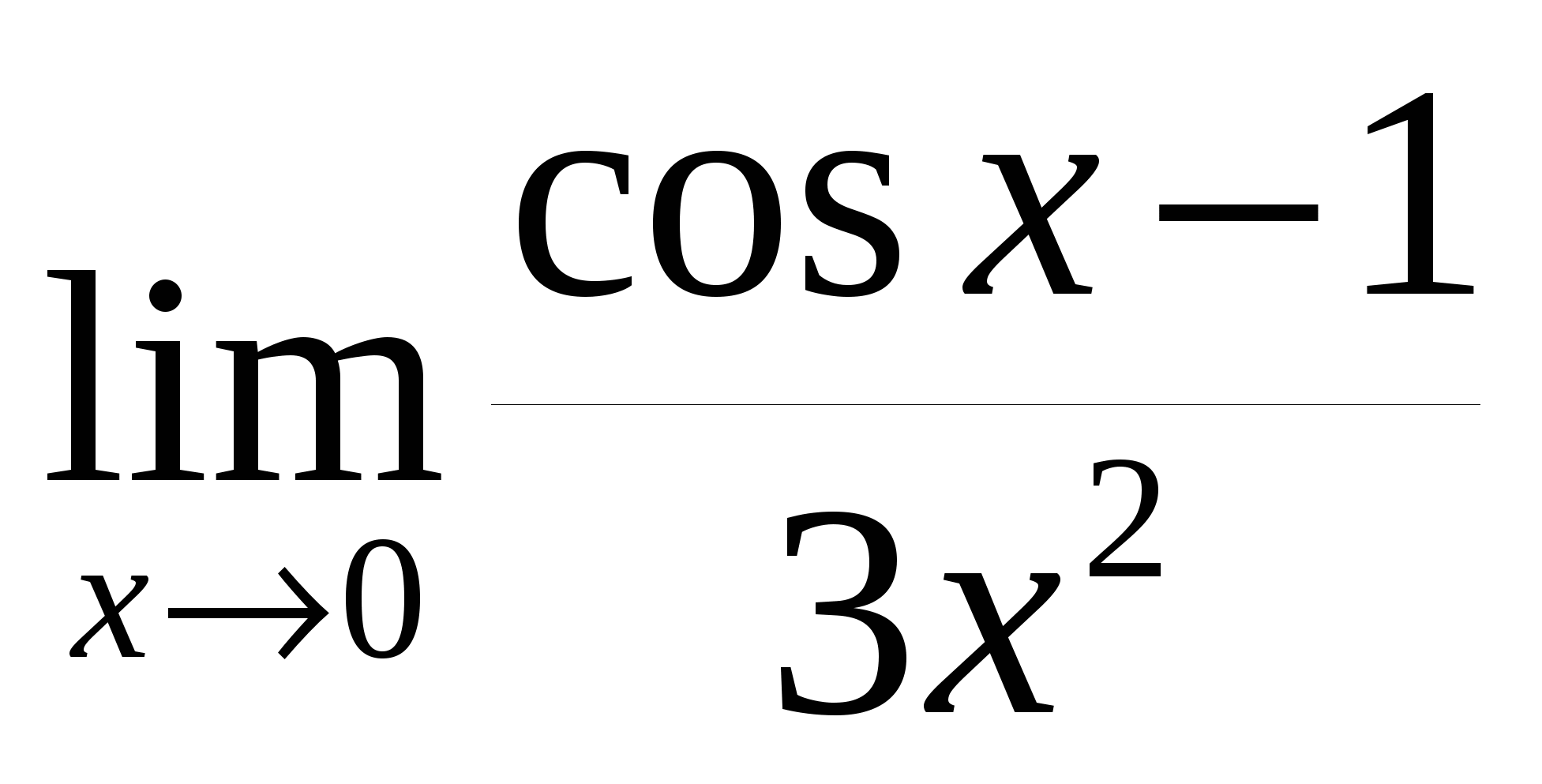 . .
По аналогии с примером 19.3 получим
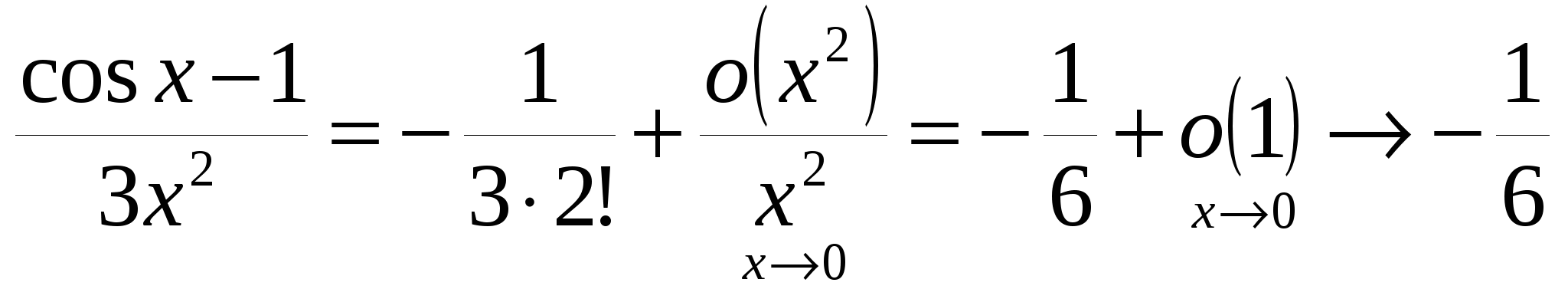 , ,
то есть 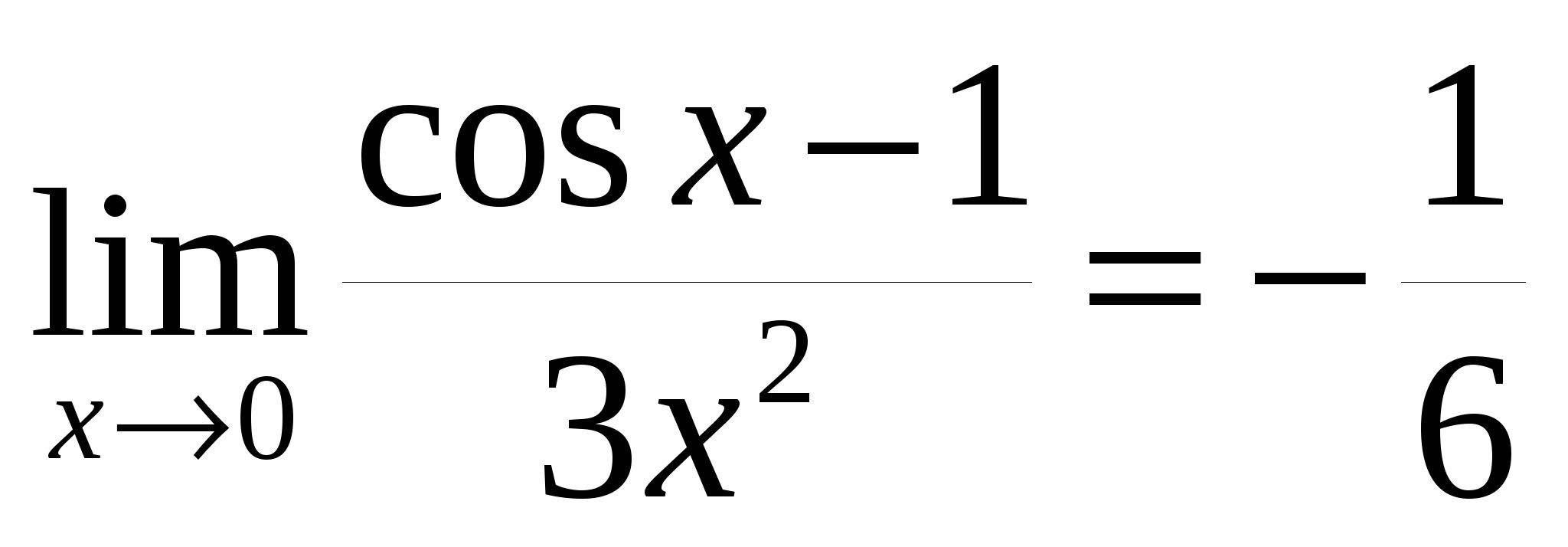 . .
4) Функция 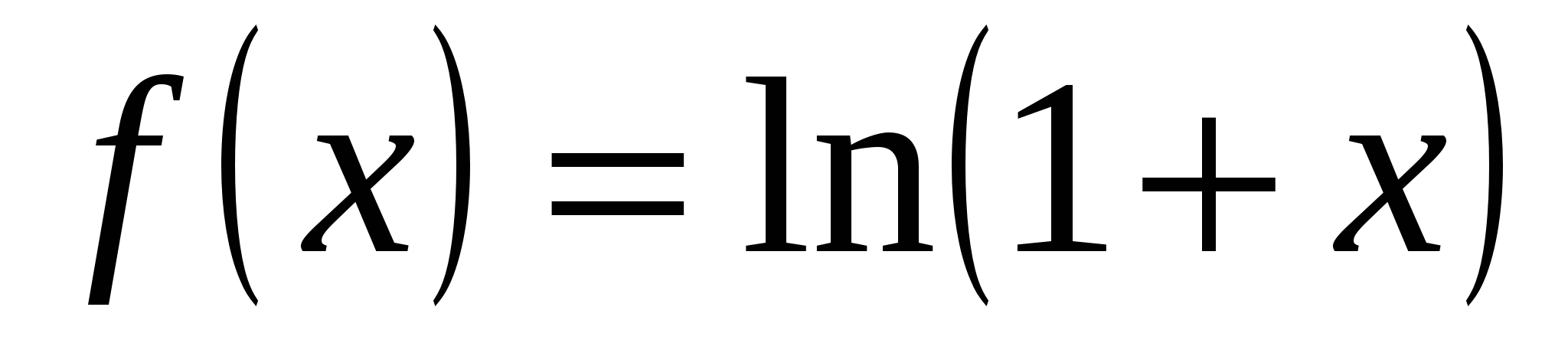 определена и сколько угодно раз дифференцируема для определена и сколько угодно раз дифференцируема для 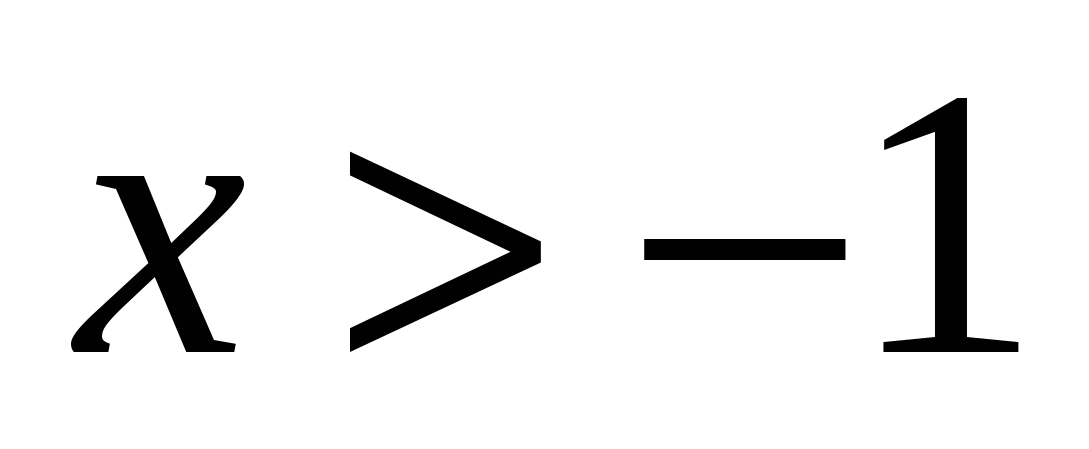 . Для . Для 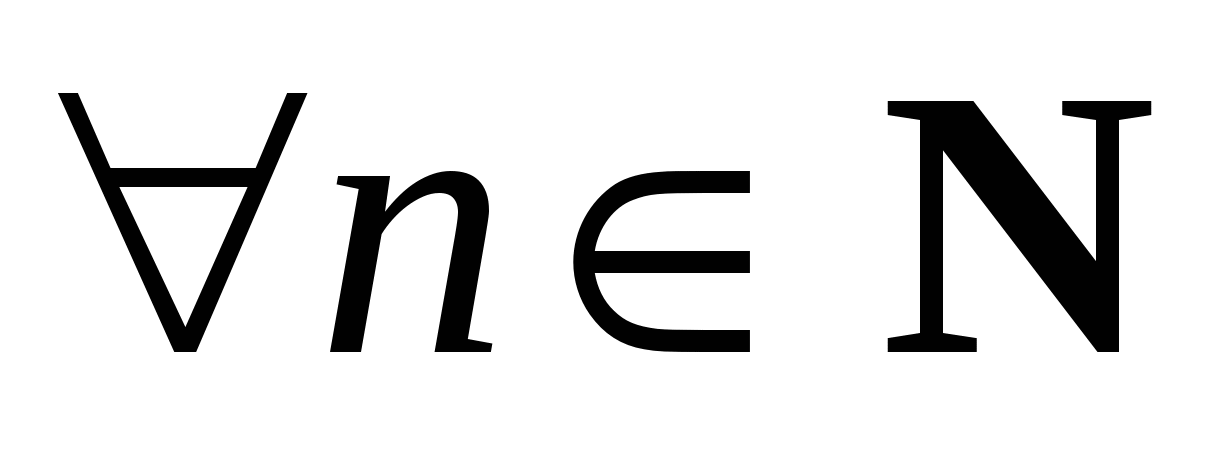 при при 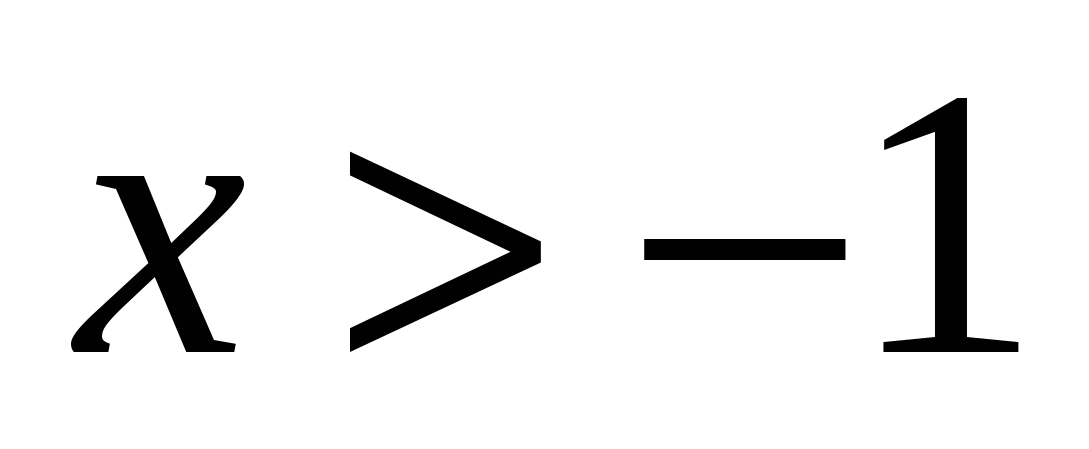 запишем формулу Тейлора. Так как запишем формулу Тейлора. Так как 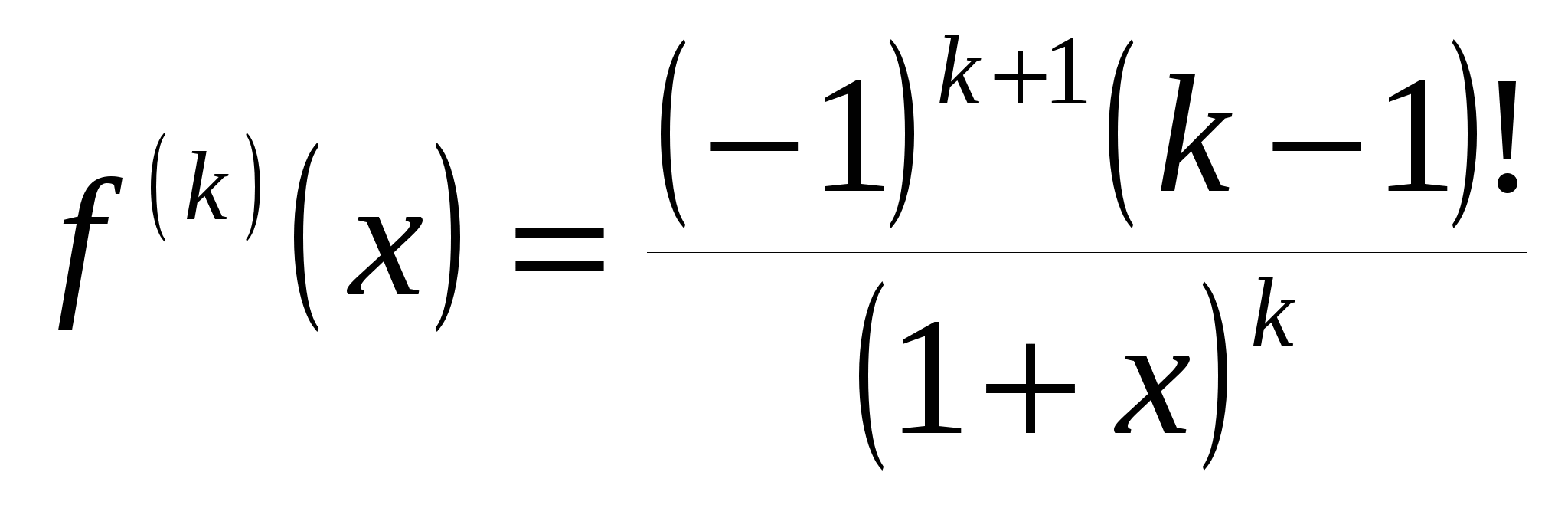 , , 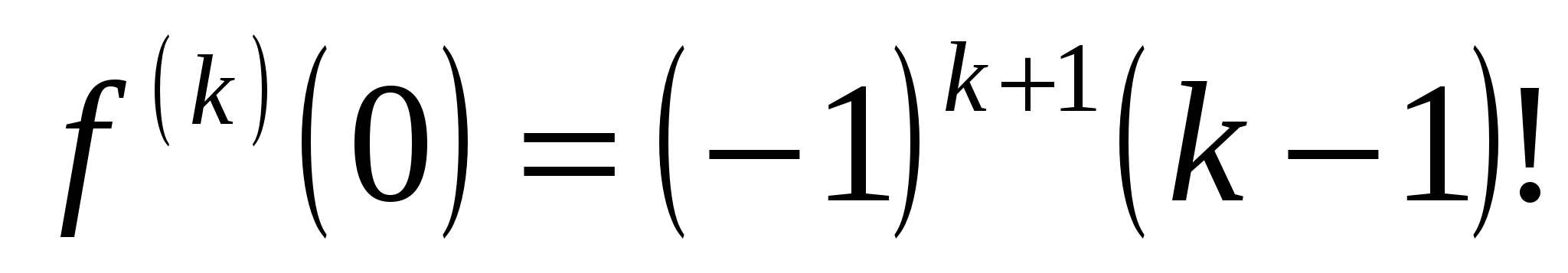 , то формула Тейлора имеет вид: , то формула Тейлора имеет вид:
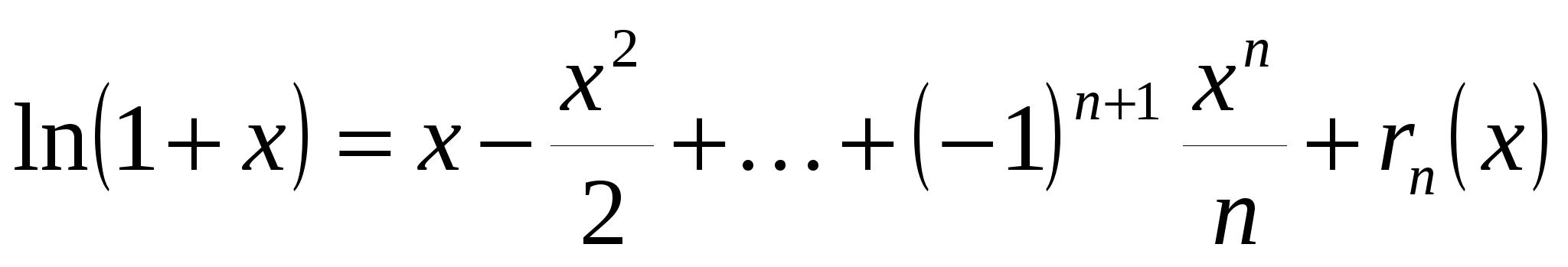 . .
При 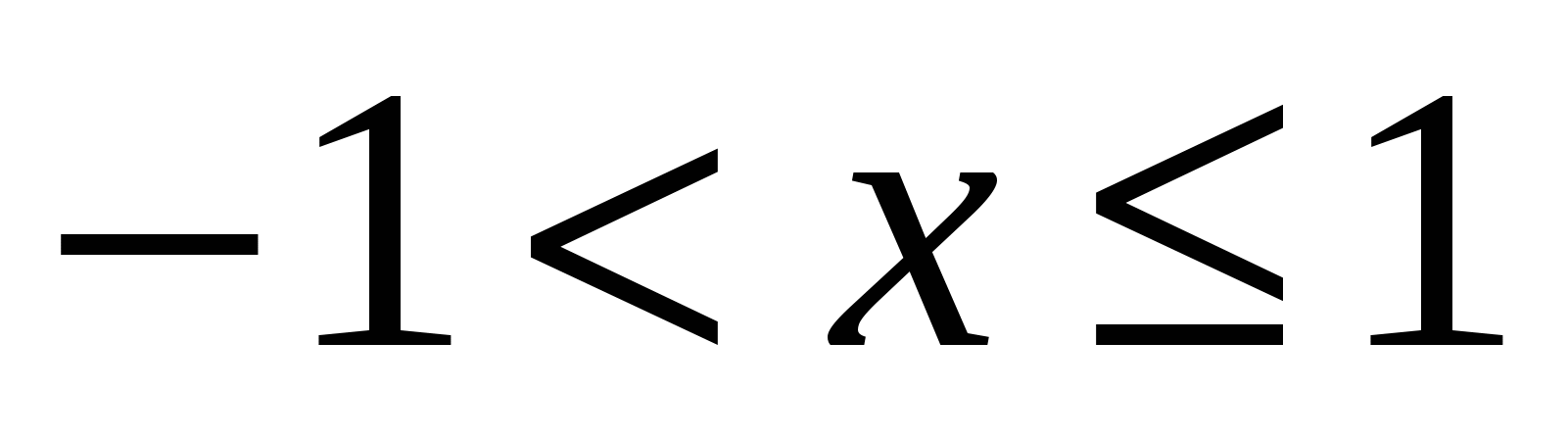 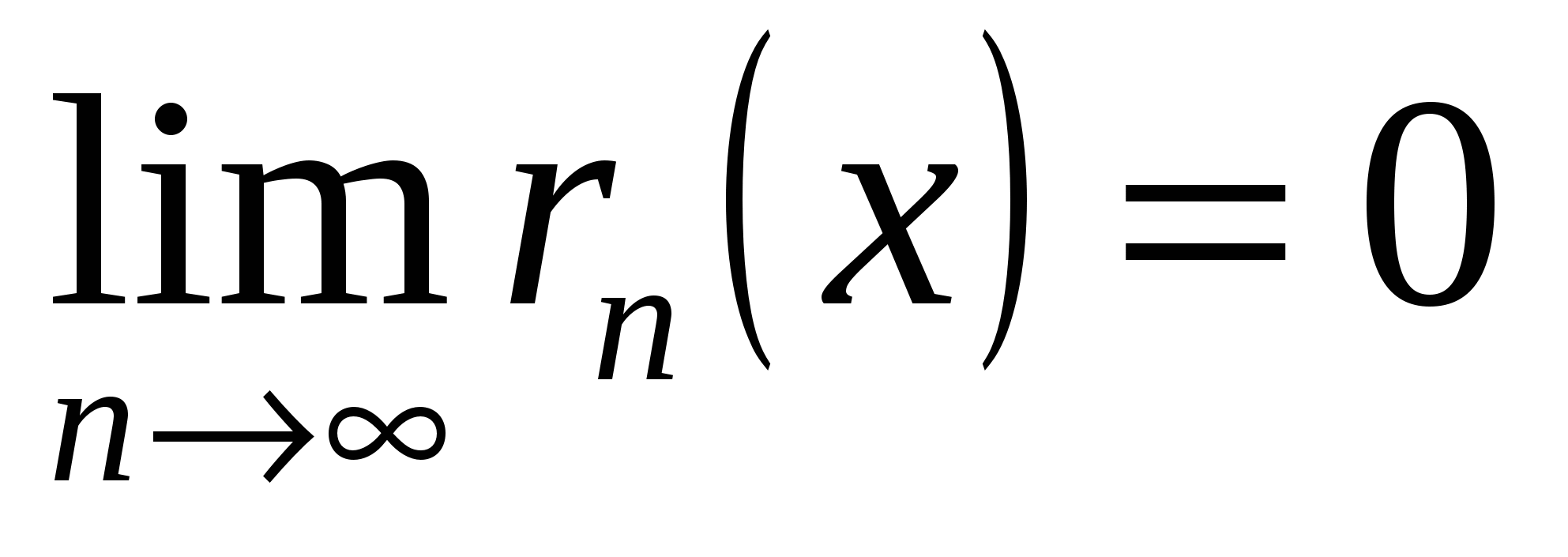 , поэтому , поэтому
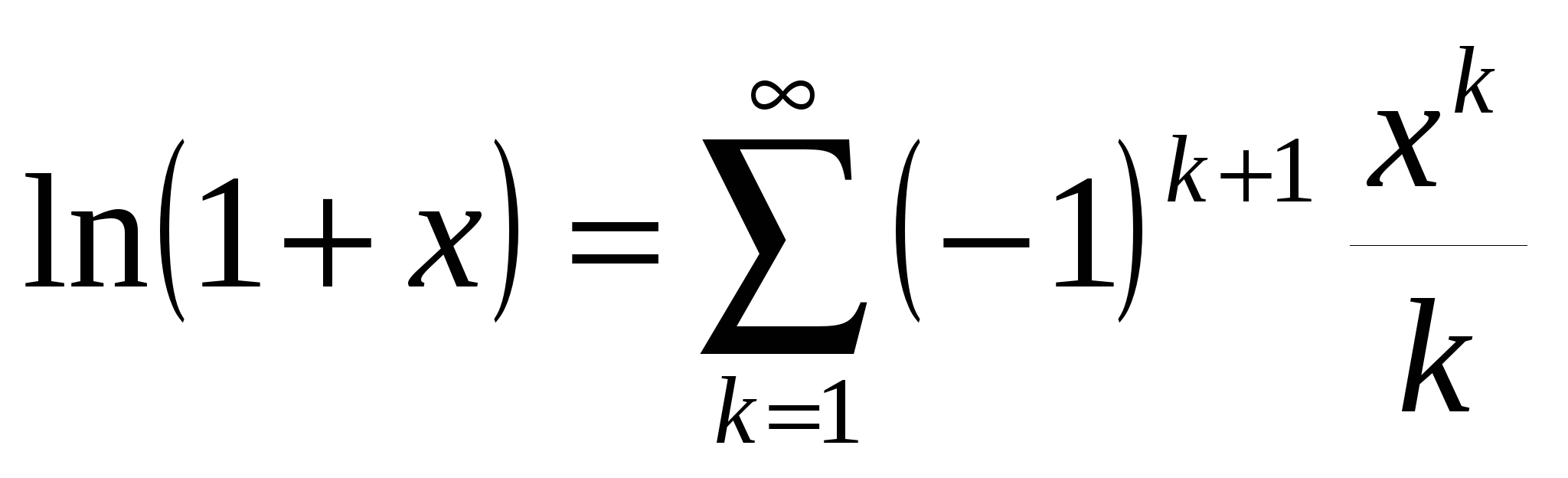 . .
Например, 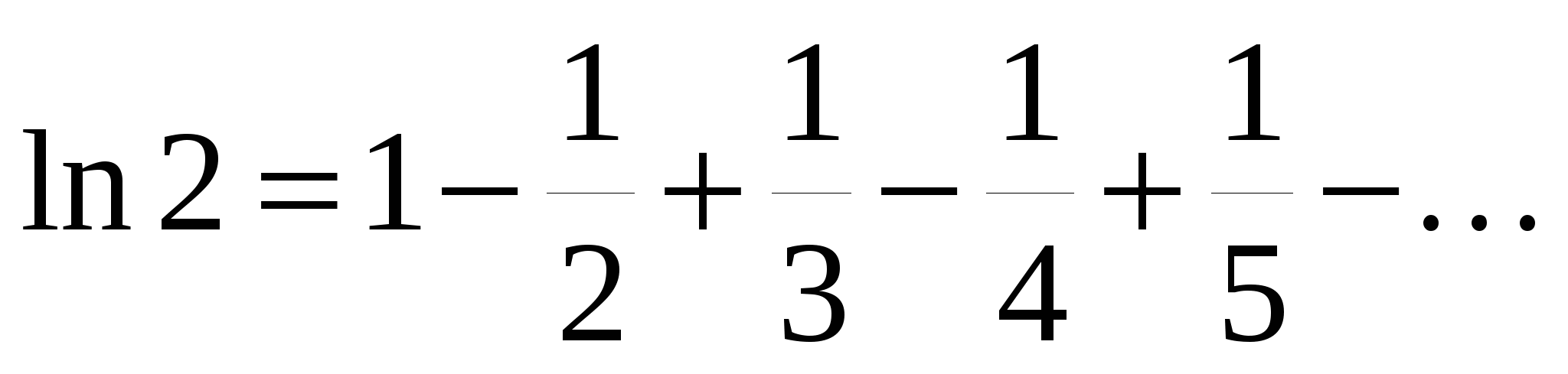 . .
5) Функция 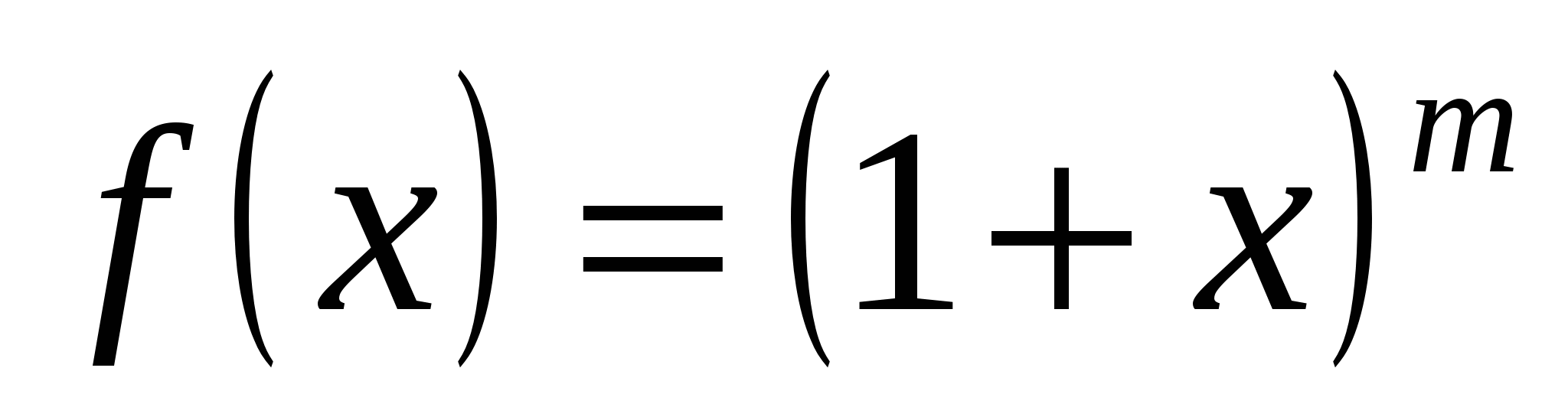 . Производные . Производные 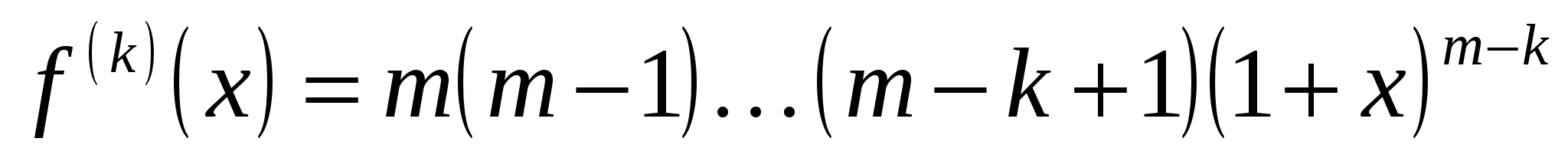 , , 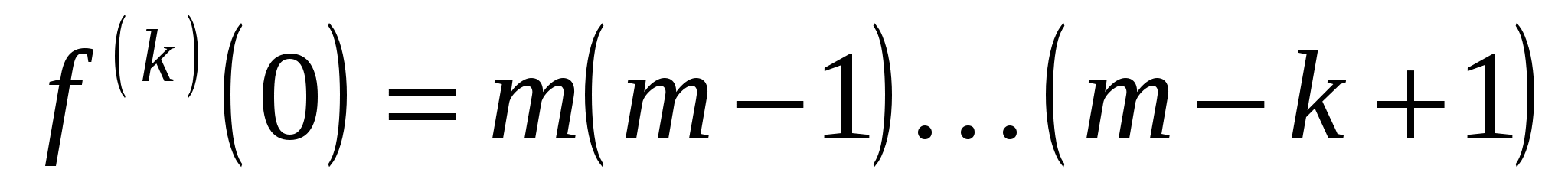 . Формула Тейлора по степеням x имеет вид: . Формула Тейлора по степеням x имеет вид:
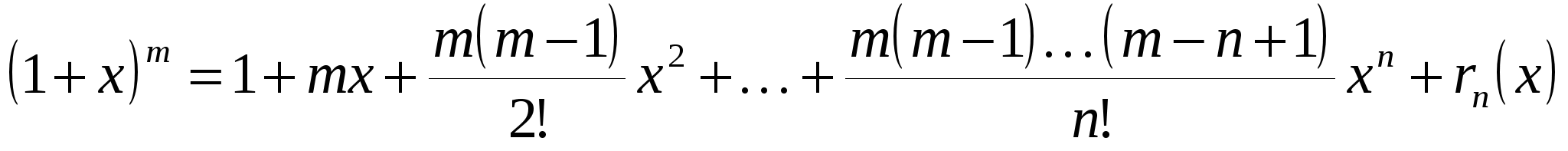 . .
Для 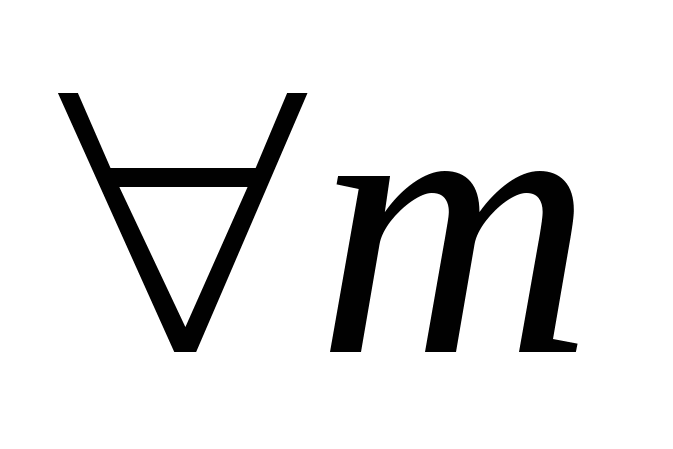 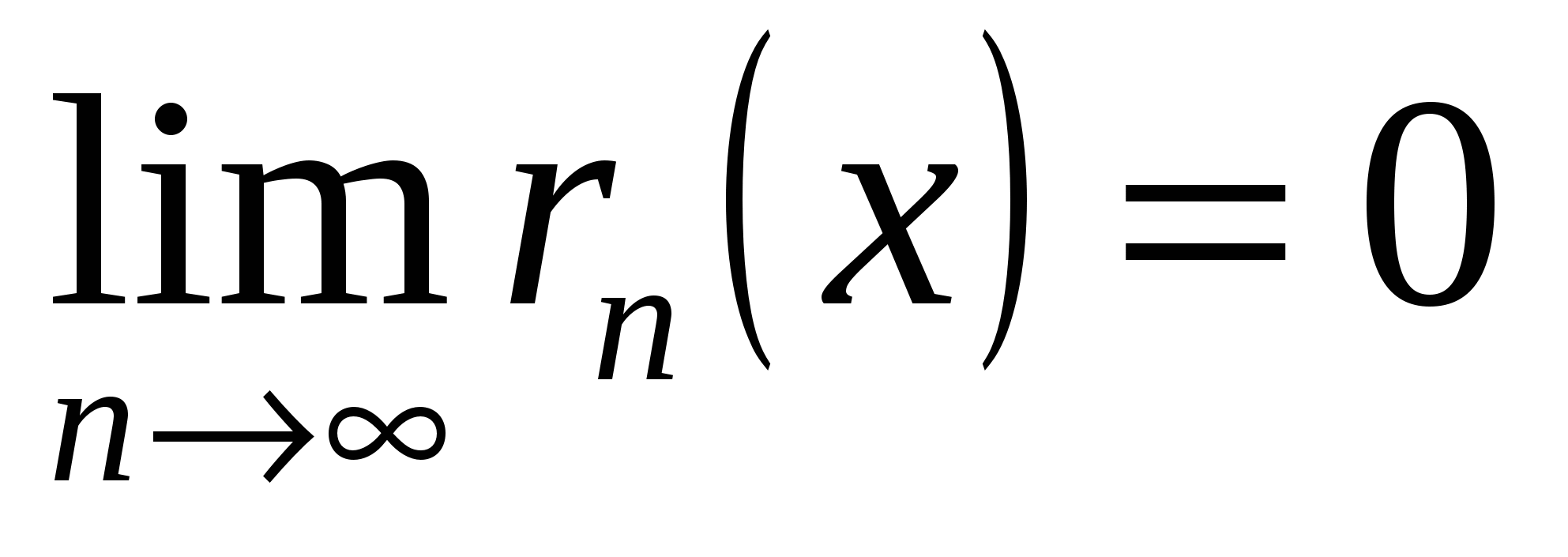 при при 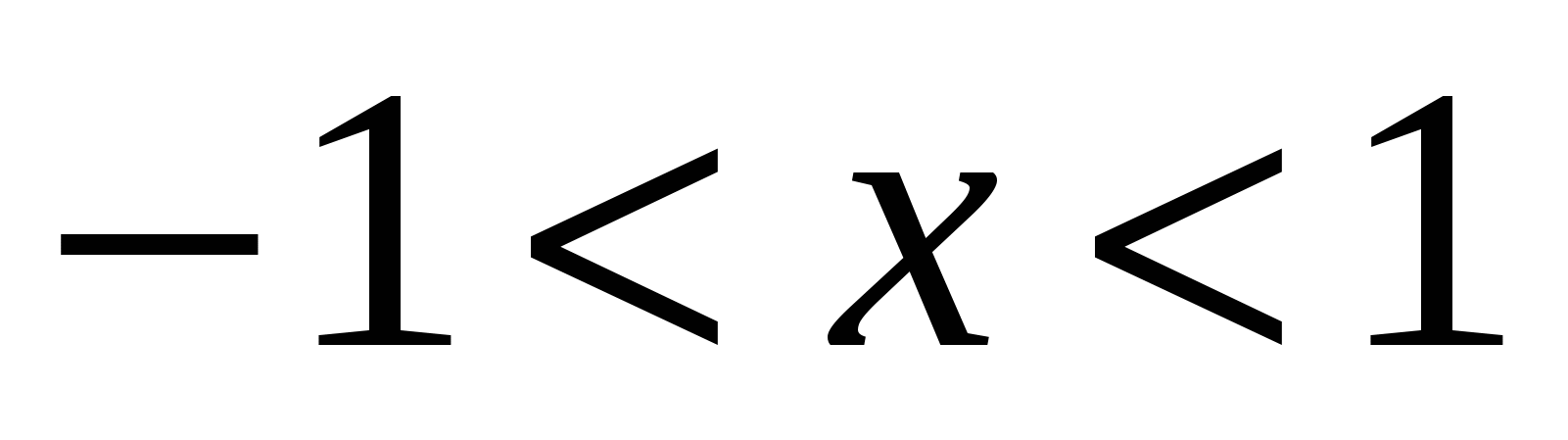 , поэтому , поэтому
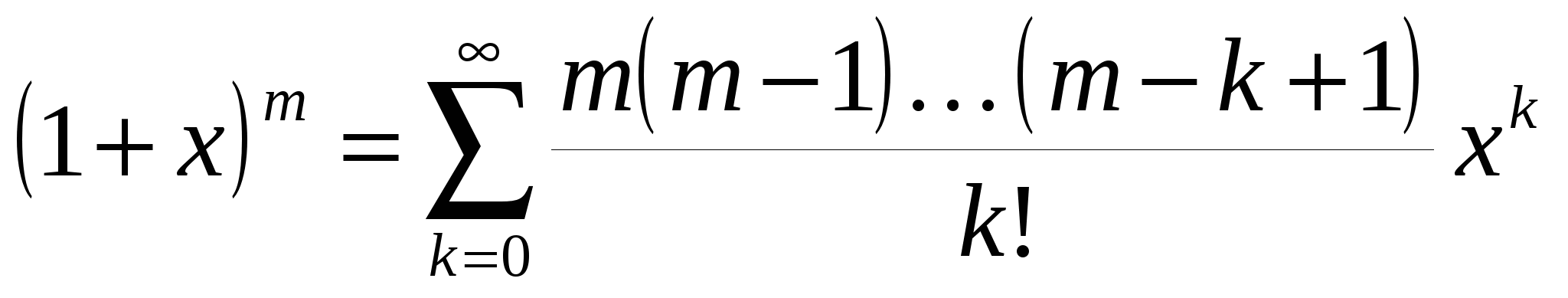 . .
Если 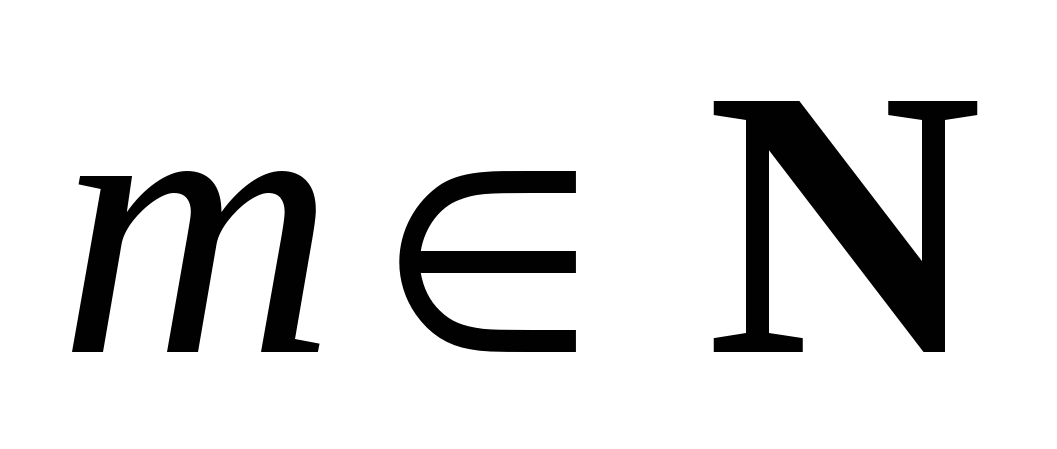 , то функция , то функция 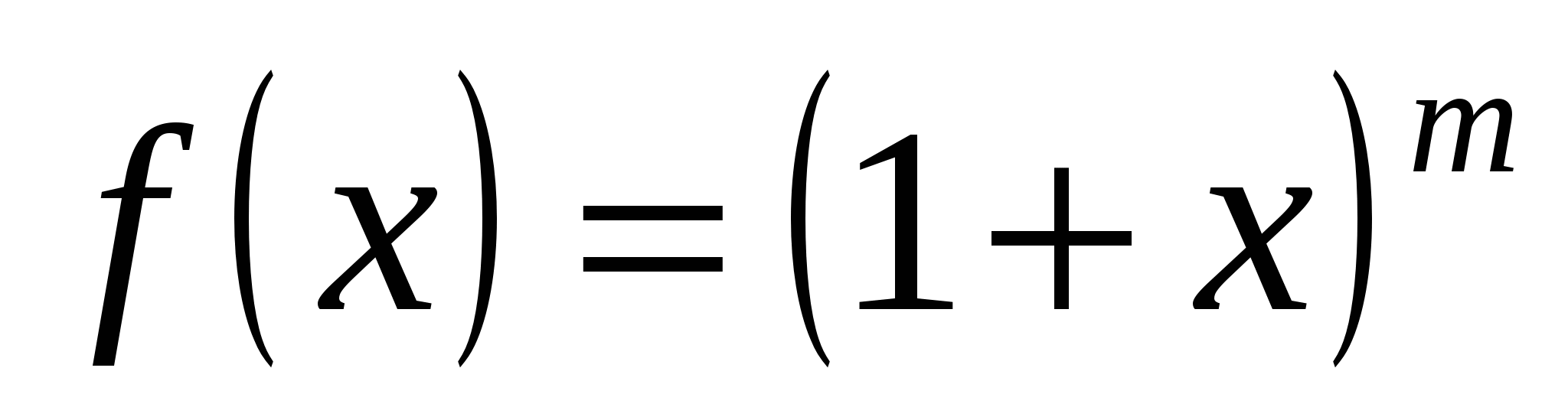 есть многочлен. В этом случае есть многочлен. В этом случае 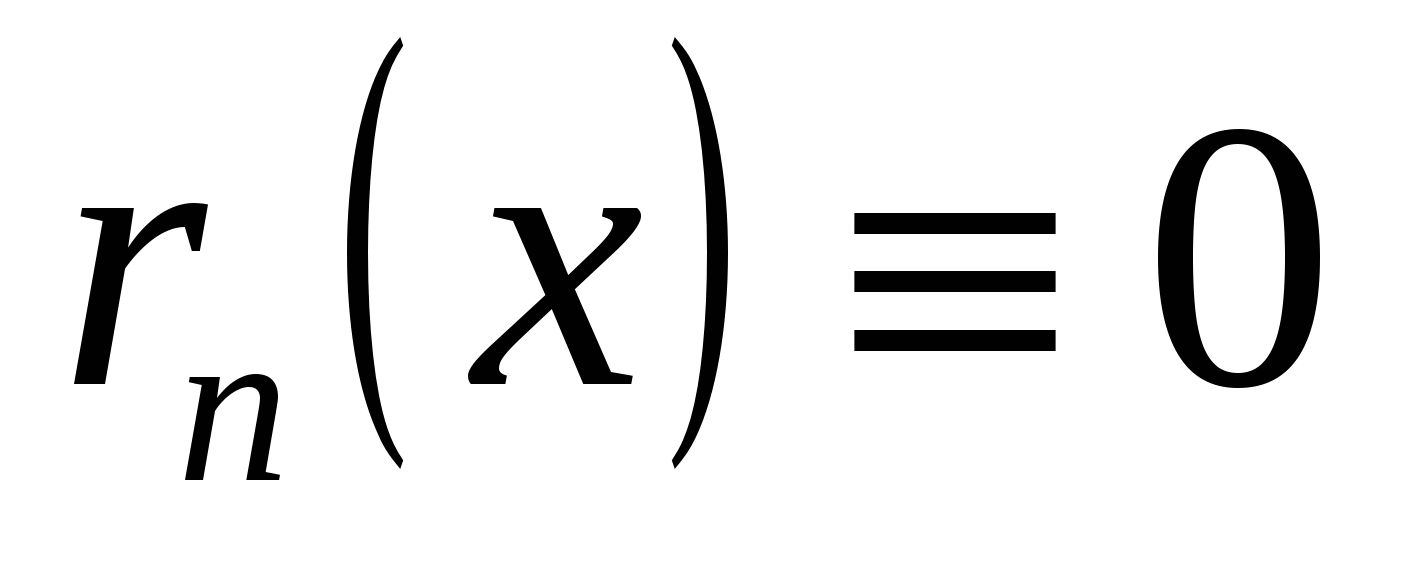 для для 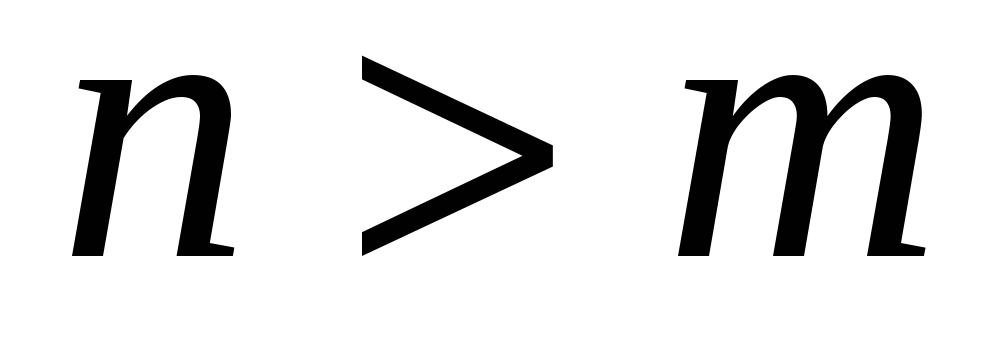 и ряд представляет собой конечную сумму – многочлен Тейлора. и ряд представляет собой конечную сумму – многочлен Тейлора.
1 Тейлор Брук (1685-1731) – английский математик.
1 Маклорен Колин (1698-1746) – шотландский математик.
2 Пеано Джузеппе (1858-1932) – итальянский математик.
|
 Скачать 362.5 Kb.
Скачать 362.5 Kb.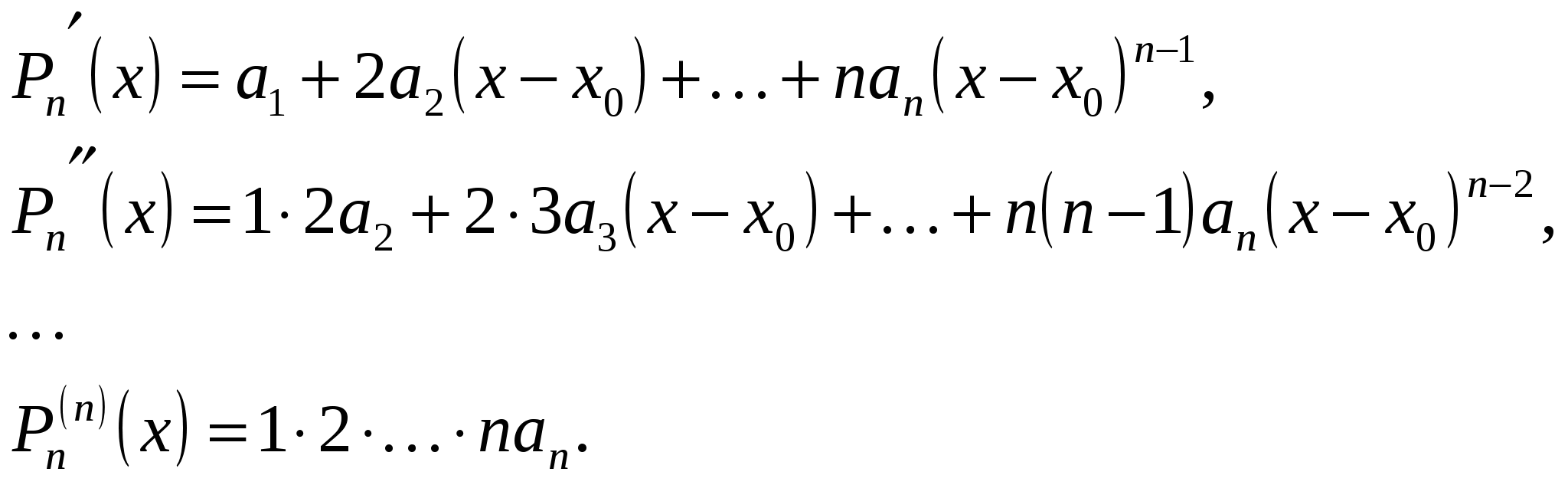 . (19.3)
. (19.3)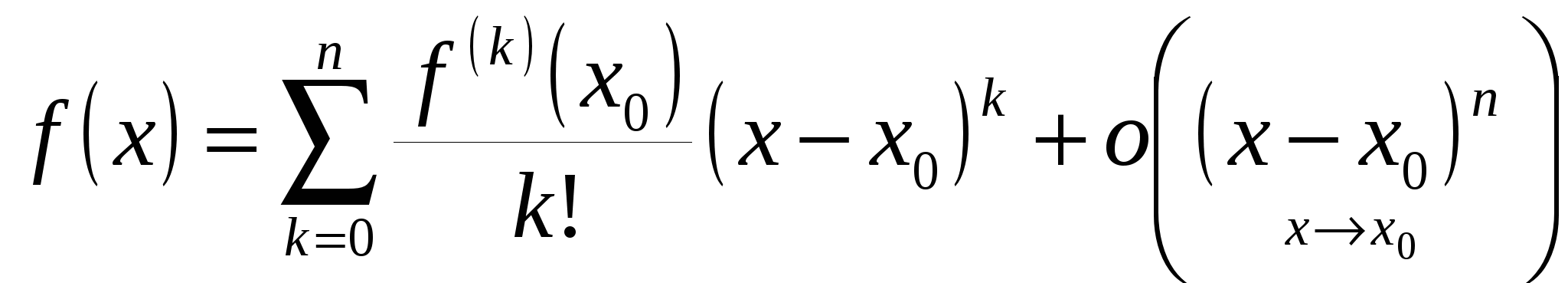 .
.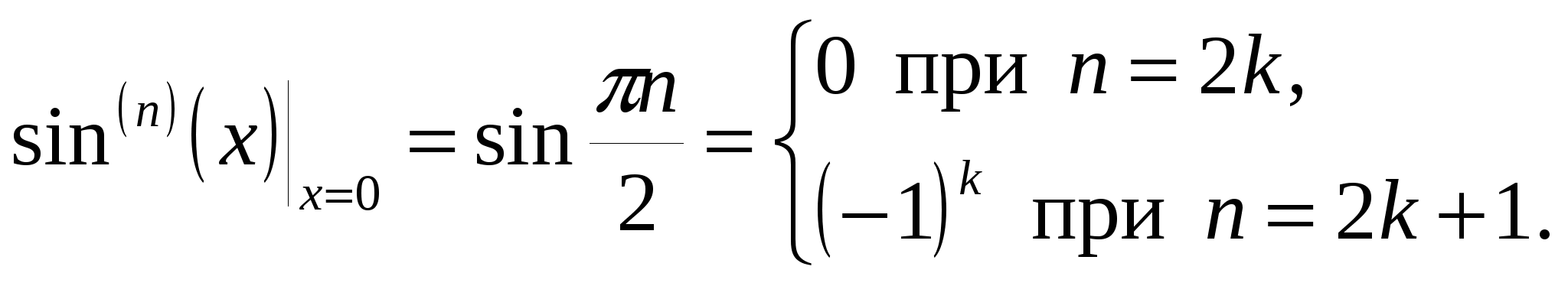
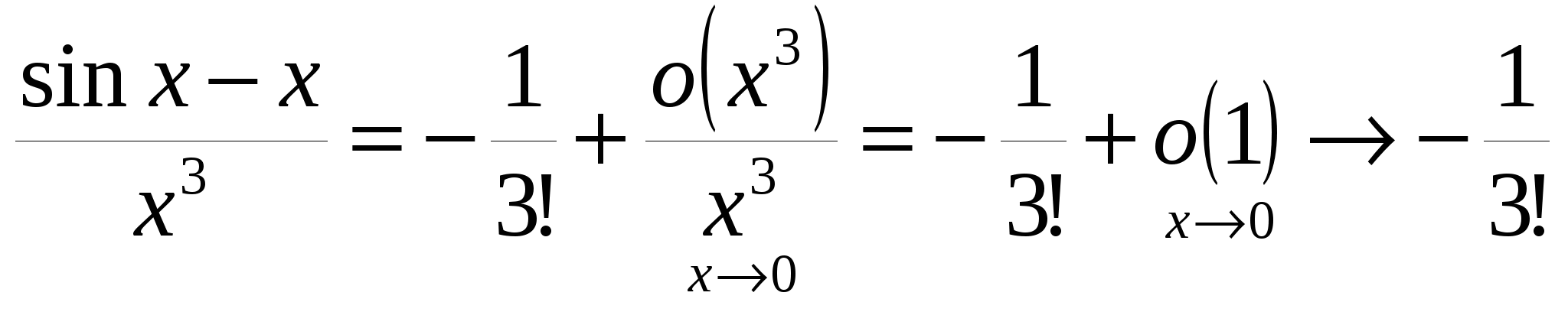 ,
,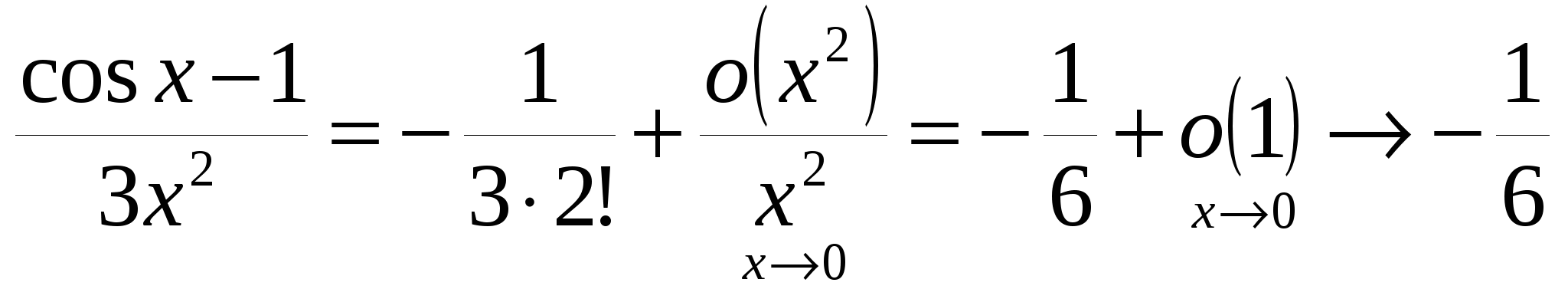 ,
,