задания (1 матан. Лекция 1рубежный контроль к разделу1 рк раздел 2
 Скачать 398.76 Kb. Скачать 398.76 Kb.
|
|
Раздел 1 ПЗ 1 Лекция 1+рубежный контроль к разделу1 РК 1. Раздел 2 ПЗ 2.Известные вам определения истории, кому принадлежат? Какое определение вы считаете наиболее отвечающим вашим представлениям РК 2. Известные вам определения культуры, кому принадлежат? Какое определение вы считаете наиболее отвечающим вашим представлениям Раздел 3 ПЗ 3. Известные вам определения математики, кому принадлежат? Какое определение вы считаете наиболее отвечающим вашим представлениям РК 3.Можно ли историю и математику отнести к области культуры Раздел 4 ПЗ 4. Тема диплома РК 4. Если есть публикации (какие? Где?), прикрепить в СДО Раздел 5 ПЗ 5. История, культура,религия и наука Вавилона РК 5. Из истории вавилонской математики Раздел 6 ПЗ 6. История, культура,религия и наука Древней Греции РК 6.Из истории древнегреческой математики Раздел 7 ПЗ 7. История, культура,религия и наука Древнего Китая РК 7. Из истории древнекитайской математики Раздел 8 ПЗ 8. История, культура,религия и наука Древней Индии РК 8. Из истории древнеиндийской математики Раздел 9 ПЗ 9. История, культура,религия и наука Древней Руси РК 9. Из истории древнерусской математики Раздел 10 ПЗ 10. История, культура,религия и наука Древней (Киевской) Руси РК 10. Из истории древнерусской математики Раздел 11. ПЗ 11. История, культура и наука Древнего Египта РК 11. Из истории древнеегипетской математики Раздел 12. ПЗ 12. Пантеон древнеегипетских богов РК 12. Древнеегипетский Бог ТОТ Раздел 13. ПЗ 13. Пантеон древнегреческих богов РК 13.Пантеон древнеримских богов Раздел 14. Рубежный контроль 3+ лекция к разделу 3 Для облегчения процесса расчета создаем XL-таблицу в Microsoft Excel по следующему алгоритму: В столбец А вводится название пирамиды, в столбец В вводится временной период пирамиды, в столбец С вводится династия. Это общие известные сведения о постройке.  В столбец D вводится x длина пирамиды 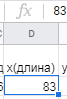 В столбец E вводится y ширина пирамиды 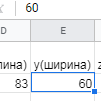 В столбец F вводится z высота пирамиды 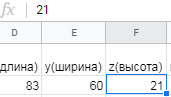 В столбце G автоматически, по введенным данным, выводится Вурф пирамиды =((D2+E2)*(E2+F2))/(E2*(D2+E2+F2)) 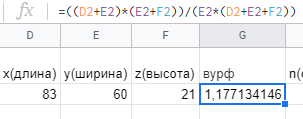 6) В столбец H вводится n количество ступеней пирамиды, если данные известны. В данном случае ячейка остается пустой. 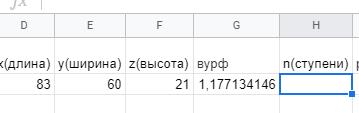 7) В столбце I автоматически, по введенным данным, рассчитывается количество ступеней пирамиды, если в столбец H ничего не введено =((F2*(2-J2))/((J2-1)*D2))-1 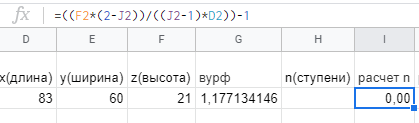 Для расчета руксона нам необходимо знать некоторые параметры, например высоту сооружения, длину стороны основания и число ступеней. Имеется формула для расчета В столбце J автоматически, по введенным данным, рассчитывается руксон пирамиды =1+F2/((H2+1)*D2+F2) 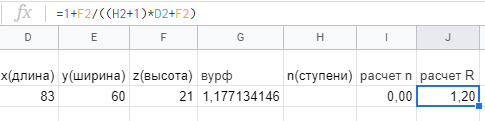 АРХИТЕКТУРА РУКСОН И ПРОПОРЦИИ ПИРАМИД ДРЕВНЕГО ЕГИПТА Игнатьев Юрий Анатольевич доцент, кандидат физико-математических наук, преподаватель математики, Образовательный комплекс «Юго-Запад», Москва Введение. Древнеегипетская математика известна в основном по двум большим письменным источникам, носящим названия «папирус Райнда» и «папирус Голенищева» [1]. Более краткие папирусы египетских писцов, имеющие отношение к математике, также были обнаружены и изучены специалистами [2]. Для дальнейшего важно знать, что древние зодчие из дельты Нила умели, говоря языком современной математики, складывать, умножать и делить натуральные числа и оперировать с дробями. Образованные люди Древнего Египта располагали понятием уравнения, и это позволит нам в дальнейшем записывать их в современных символах. Целью данного исследования является описание алгоритма вычисления руксона, описание руксоновой типологии пирамид и руксоновых архитектурных канонов, а также приемов для получения этих канонов. 1.Формула руксона. Руксоном (на английском - ruxon) архитектурного сооружения называется величина R, которая находится по следующей формуле: 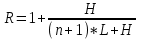 , (1) , (1)где H – высота сооружения, L – длина стороны квадратного основания, n – число ступеней (этажей) сооружения. Рассмотрим в качестве примеров пирамиды фараонов Хеопса, Джосера и Хуни. Если воспользоваться данными источников [3], то H=146,6м, L=230,348м, n=218. Производя расчеты по формуле (1), получаем значение руксона пирамиды Хеопса: 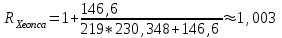 , (2) , (2) Рис. 1. Пирамида фараона Хеопса. Фото: архив авторов. Для пирамиды Джосера берем n=6 и H=61м [4]. Однако, ее основание является не квадратом, а прямоугольником 125м на 115м. Произведем расчет для обоих значений L по формуле (1): 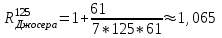 , (3) , (3)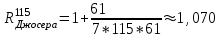 , (4) , (4)Эти величины отличаются друг от друга лишь на 0,005, т.е. практически одинаковы. По-видимому, этот факт, а также экономический расчет привели зодчих Древнего Египта к мысли, что использовать прямоугольник в основании пирамиды неудобно и невыгодно. Большинство пирамид действительно имеет практически квадратное основание.  Рис. 2. Пирамида фараона Джосера. Фото: архив авторов. Пирамида фарална Хуни, которая была достроена фараоном Снофру, имела восемь ступеней, т.е. n=8 [5]. По данным работы [6], H=118м и L=146м. Производя расчет по формуле (1), получаем: 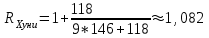 , (5) , (5) Рис. 3. Пирамида фараона Хуни. Фото: архив авторов. Как следует из формулы (1), руксон обладает следующими свойствами: -это безразмерная величина, -ее значение лежит между единицей и двойкой: 1 R 2 ; -для полной и усеченной правильной пирамиды с квадратным основанием значение руксона совпадает со значением вурфа этой пирамиды, поскольку в обоих случаях n=1[6]. 2.Руксоновая типология пирамид. Пусть открытый интервал (1,2) разбит на N частей, так что координаты точек разбиения находятся по формуле: 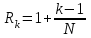 , (6) , (6)где k=1,2,3,…,N,N+1.Теперь подставим (6) в формулу руксона (1), и после некоторых математических преобразований получим: 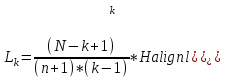 , (7) , (7)где параметр k принимает значения, что и в равенстве (6), но его значения 1 и (N+1) исключаются. И это исключение необходимо по физическому смыслу, при k=1 длина стороны основания пирамиды оказывается равной бесконечности, а при k=N+1 становится бесконечной высота пирамиды. Перебирая допустимые значения величины k, получаем (N-1) типичных форм пирамид, которые, варьируя значение N, можно использовать для нахождения пропорций всех известных сегодня пирамид Древнего Египта. Аналогичная типология пирамид с помощью понятия вурфа была построена, например, в работе [4]. Однако, вурфовая типология не учитывает количество ступеней или рядов кладки пирамиды n, т.е. является более грубым инструментом по сравнению с руксоновой типологией. Тем не менее, вурфовая типология имеет важное значение для тех пирамид, которые были облицованы мрамором для придания им правильной геометрической формы. 3. Руксоновые каноны. Руксоновым каноном, использованным египетскими зодчими, будем называть уравнение: R=C (8) где R – руксон, С – некоторая постоянная величина. Эта формула является, очевидно, обобщением формулы вурфового какона (см. формулу (5.1) в публикации [4,с.18]). Будем предполагать в дальнейшем, что каждая династия фараонов Древнего Египта возводила свои пирамиды, используя определенное значение константы С. Тогда для нахождения этого значения можно воспользоваться, например, следующими двумя способами: -Метод усреднения по династиям: пусть для одной из династий фараонов имеются пирамиды со значениями руксонов R1, R2, R3... Rm , где m – некоторое известное натуральное число; тогда значение С для этой династии можно найти по формуле: 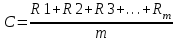 , (9) , (9)-Треугольный метод А.В. Куниловской: пусть имеются руксоны m пирамид одной из династий фараонов Древнего Египта; упорядочим эти числовые значения по возрастанию: R1 R2... Rm-1 Rm ; для каждых двух соседних значений руксонов RiRi+1 , где i=1,2,3,…,(m-1), найдем среднее значение 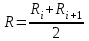 для всех i; получаем новую последовательность значений: R1, R2, R3,...Rm-2, Rm-1, которая на одно значение короче предыдущей последовательности; повторяя теперь эту процедуру (m-1) раз, приходим к одному значению, которое и принимается в качестве С. для всех i; получаем новую последовательность значений: R1, R2, R3,...Rm-2, Rm-1, которая на одно значение короче предыдущей последовательности; повторяя теперь эту процедуру (m-1) раз, приходим к одному значению, которое и принимается в качестве С.Таблица 2. Значения руксоновых канонов некоторых династий фараонов Древнего Египта [4]
4. Обсуждение полученных результатов. Как видно из формулы (3) и Таблицы 1, величина руксона для пирамиды Хеопса значительно ближе к единице, чем у других известных своими пропорциями пирамид Древнего Египта. Это могло послужить одной из многих причин, почему пирамида Хеопса была отнесена к множеству семи «чудес света». Таблица 1. Руксоны и вурфы некоторых пирамид Древнего Египта
Руксоновая типологизация всех пирамид властителей древних царств в дельте Нила является задачей будущих исследований. Для ее решения потребуется, как представляется естественным, восстановить с помощью руксона высоты разрушенных временем и варварами пирамид способом, аналогичным тому, который был предложен для вурфового метода в работе [4]. Результат этой руксоновой типологизации будет иметь важное значение в наше время, когда археологи и другие исследователи архитектуры Древнего Египта, в том числе сотрудники Немецкого археологического института, стремятся найти единообразный метод для обобщения всех научных знаний о пирамидах этой высокоразвитой цивилизации. Хорошим помощником археологу может послужить пирамидальный руксометр, изобретенный А.В. Куниловской на основе ее же пирамидального вурфометра [4], который позволяет на удалении от пирамиды определить примерное значение ее руксона. Научная гипотеза о существовании вурфовых, а теперь уже и руксоновых канонов, у египетских зодчих того времени, не встретила возражений у специалистов. Однако, следует признать справедливым, что она может быть уточнена с помощью археологических изысканий в будущем. Также представляется вероятным, что скоро будут предложены другие методы, кроме метода усреднения по династиям и треугольного метода, для нахождения вурфовых и руксоновых канонов. Благодарности. Автор выражает благодарность сотрудникам Каирского отделения Немецкого археологического института (DAI Kairo) за предоставление новейших данных по пирамидам Древнего Египта. Особую благодарность автор выражает профессорам, докторам архитектуры В.М. Фирсанову и Б.С. Истомину за поддержку данного направления исследований. Список литературы 1. История математики с древнейших времен до начала XIX столетия. / Под ред. А.П. Юшкевича. – Том 1: С древнейших времен до начала Нового времени. – Москва, 1970. 2. Кларк С., Энгельбах Р. Строительство и архитектура в Древнем Египте. – Москва, 2009. 3. www.khufu.dk Khufu dimensions. 4. Игнатьев Ю.А. Элементы вурфового анализа в теоретической архитектуре. – Москва, 2010. 5. www.egyptologia.com Пирамиды Хуни. 6. Игнатьев Ю., Куниловская А., Варечкина О. Колоссальный пирамидион фараона Снофру. // Россия и Германия. Научный гумбольдтовский ж Раздел15 ПЗ 15. Рубежный контроль+ лекция 2 РК 15 Раздел16 ПЗ 16. Рубежный контроль+ лекция 4 РК 16 |
