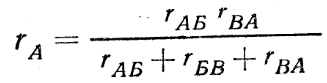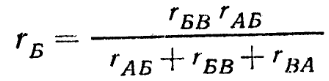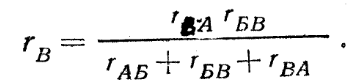Лекция 2 Эквивалентные преобразования электрических цепей. Лекция 2 Эквивалентные преобразования электрических цепей

• Название: Лекция 2 Эквивалентные преобразования электрических цепей
• Анкор: Лекция 2 Эквивалентные преобразования электрических цепеи
• Дата: 06.11.2020
• Размер: 1.11 Mb.
• Имя файла: Лекция 2 Эквивалентные преобразования электрических цепей.doc
• Тип: Лекция; #148365

Лекция 2 Эквивалентные преобразования электрических цепей
2.1 ИСТОЧНИК ЭЛЕКТРИЧЕСКОЙ ЭНЕРГИИ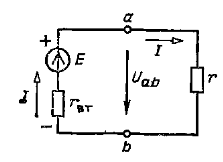


Рис. 2.1 Простейшая электрическая цепь постоянного тока
С изменением сопротивления rприемника (рис. 2.1) напряжение источника электрической энергии

(2.1)

изменяется от значения U_x = E при холостом ходе (r = ∞) и I = I_x = 0 до нуля при коротком замыкании (r = 0) и I = I_к = E/r_вт = U_x/ r_вт.

Зависимость напряжения U(I), показанная на рис. 2.2,a, называется внешней харак­теристикой источника. Это прямая линия. По за­данной внешней характеристике можно найти параметры источника Е и r_вт = E/I_к.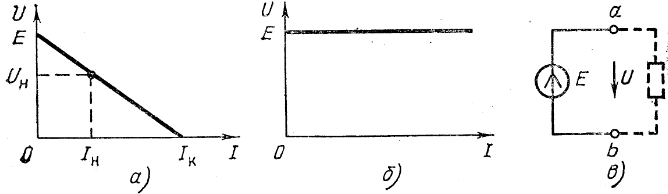



Рис. 2.2 Внешние характеристики реального (а) и идеального (б) ис­точников ЭДС, обозначение, идеального источника ЭДС (в)
Если можно пренебречь внутренним сопротивлением ис­точника (r_втмного меньше r),то, считая r_вт = 0, получим U = E— постоянное, т. е. не зависит от тока I (рис. 2.2,б). Такой источник называется идеальным источником ЭДС или напряжения. Схема замещения идеального источника ЭДС пред­ставлена на рис. 2.2,в. Схема замещения реального ис­точника состоит из идеального источника ЭДС и соединен­ного с ним последовательно внутреннего сопротивления (рис. 2.1).

2.2 ЗАКОНЫ КИРХГОФА
Электрическая цепь называется линейной, если она со­держит только линейные элементы. Линейным называется элемент цепи, сопротивление которого остается постоянным независимо от значений и направлений тока в нем и напряжения на его выводах.

При расчете режима работы электрической цепи очень часто необходимо определить токи, напряжения и мощности на всех ее участках при заданных ЭДС источников и со­противления участков цепи.

Такой расчет основан на применении законов Кирх­гофа, для записи которых введем понятия ветви, узла и контура, а также двухполюсника.

Ветвью электрической цепи называется ее участок, состоящий из одного или нескольких элементов, соединен­ных так, что по ним проходит один и тот же ток. Такое сое­динение элементов называется последовательным. Например, ветвь, состоящая из одного источника питания с ЭДС Е и внутренним сопротивлением r_вт и резистора с сопротивлением r, показана на рис. 2.3. Остальные участ­ки цепи на этом рисунке не показаны.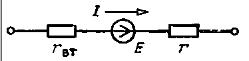



Рис. 2.3 Ветвь электрической цепи
Точка электрической цепи называется узлом (точкой разветвления), если в ней соединены три или большее чис­ло ветвей или проводов.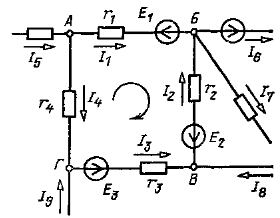



Рис. 2.4 Часть схемы электрической цепи
На рис. 2.4 показана часть схемы замещения цепи и ее четыре узла (А, Б, В, Г). В узле А соединены три ветви с токами I₁, I₄, I₅, в узле Б соединены четыре ветви с тока­ми I₁, I₂, I₆, I₇.

Контур электрической цепи представляет собой замк­нутый путь, проходящий по нескольким ветвям, например контур из четырех ветвей на рис. 2.4.

Часть электрической цепи с двумя внешними выводами (полюсами), которыми она может присоединяться к другим ветвям или участкам, называется двухполюсником. Двухполюсник, не содержащий источников питания, назы­вается пассивным, а содержащий источник питания — ак­тивным.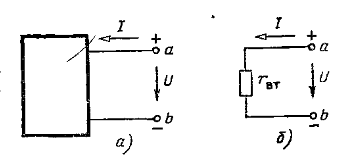



Рис. 2.5 Пассивный двухполюсник (а) и его схема замещения (б)
Упассивного двухполюсника, обозначение которого показано на рис. 2.5,а, выбирают одинаковое на­правление напряжения и тока относительно его выводов а и bтак же, как у резисторов, т. е. U=U_ab=φ_a – φ_b. Отно­шение U/I=r_вх=r_втназывают входным или внут­ренним сопротивлением пассивного двухполюс­ника.

Если при заданном напряжении Uзаменить двухполюс­ник его входным сопротивлением (рис. 2.5,б), то не изме­нится ток I. И, наоборот, при заданном токе I не изменится напряжение U.

При постоянных токах в цепи ни в одной из ее точек не могут накапливаться электрические заряды, так как это вы­звало бы изменение потенциалов точек цепи и напряжений на участках. Следовательно, электрические заряды, прите­кающие к какому-либо узлу по одной части присоединен­ных к нему ветвей или проводов в единицу времени, равны зарядам, оттекающим от этого узла по другой части ветвей или проводов за ту же единицу времени. Это положение вы­ражает первый закон Кирхгофа, который форму­лируется так: сумма токов, направленных к узлу, равна сум­ме токов, направленных от узла.

Пользуясь этим законом, например, для узлов А и Б рис 2.4 можно написать

I₁ + I₄ = I₅; I₆ + I₇ = I₁ + I₂

или

I₁ + I₄ - I₅ = 0;

I₆ + I₇ - I₁ - I₂ = 0.

В общем виде

,

т. е. алгебраическая сумма токов в узле равна нулю, при­чем со знаком плюс записываются оттекающие токи, а со знаком минус притекающие (или наоборот).

Если направления токов в ветвях не известны, то при составлении уравнений по законам Кирхгофа их необходи­мо предварительно выбрать произвольно и обозначить на схеме стрелками. В действительности направления токов в ветвях могут и не совпасть с произвольно выбранными. Поэтому выбранные направления токов называют поло­жительными направлениями. Если в результате расчета цепи какие-либо токи будут выражены отрицатель­ными числами, то действительные направления этих токов обратны выбранным положительным.

Для контура электрической цепи, изображенного на рис. 2.4, стрелками показаны положительные направления то­ков. Источники электрической энергии, внутренними сопро­тивлениями которых можно пренебречь или внутренние со­противления которых учтены в значениях сопротивлений ветвей r₁, r₂, r₃, обозначены кружками со стрелками, пока­зывающими направления действия ЭДС.

Перенеся все падения напряжения в правую часть урав­нения, найдем, что

,

или в общем виде



Это уравнение выражает второй закон Кирхго­фа: в замкнутом контуре электрической цепи алгебраиче­ская сумма ЭДС равна алгебраической сумме падений напряжения на всех сопротивлениях. При составлении урав­нений по второму закону Кирхгофа ЭДС записывается со знаком «+», если ее направление совпадает с направлени­ем произвольно выбранного обхода контура. В противном случае ЭДС записывается со зна­ком «-». Падение напряжения на сопротивлении записыва­ется со знаком «+», если направление тока в нем совпадает с направлением обхода.
2.3 СОЕДИНЕНИЕ ЗВЕЗДОЙ И ТРЕУГОЛЬНИКОМ
Схему соединения трех ветвей, образующих замкнутый контур с тремя узлами А, Б, В (рис. 2.6, а), называют треугольником.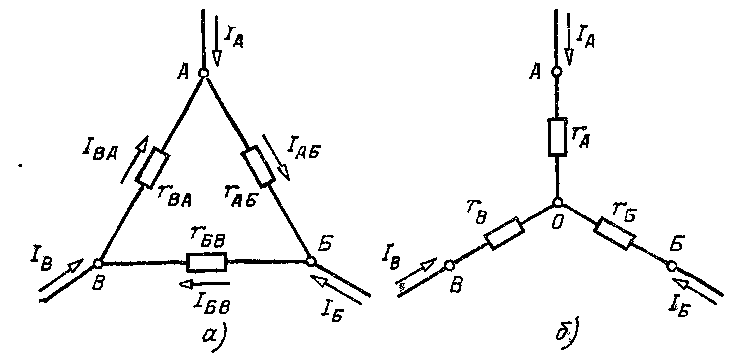



Рис. 2.6 Соединение резисторов треугольником (а) и звездой (б)
В некоторых случаях расчет сложной цепи значительно упрощается, если треугольник сопротивлений заменить звездой сопротивлений, т. е. тремя ветвями, имеющими дополнительный общий узел О (рис. 2.6, б). В других случаях расчета цепей встречается необходимость звезду заменить треугольником. Эти взаимные замены треугольника и звезды сопротивлений должны быть эквивалентными, т. е. при соответственно равных напряжениях между вершинами А, Б и В треугольника и звезды токи I_А, I_Б, I_В в подводящих проводах, соединяющих эти вершины с остальной частью цепи, должны остаться без изменений. Равенство токов должно выполняться при любых изменениях и переключениях в остальной части цепи и, в частности, при обрывах некоторых ее ветвей.

_{Сопротивления эквивалентной звезды rА, rБ, rВ находятся в определенных соотношениях с сопротивлениями треугольника rАБ, rБВ, rВА. Чтобы преобразовать треугольник в звезду при заданных сопротивлениях сторон треугольника, rАБ, rБВ, rВА требуется определить сопротивления лучей эквивалентной звезды rА, rБ, r}В.

	(2.2)
	(2.3)
	(2.4)

Таким образом, сопротивление луча эквивалентной звезды равно произведению сопротивлений двух сторон треугольника, которые присоединены к той же вершине, что и луч звезды, деленному на сумму сопротивлений всех сторон треугольника.

Если сопротивления треугольника равны друг другу: r_АБ=r_БВ=r_ВА=r_∆,то будут равны друг другу и сопротивления звезды, т.е. .

(2.5)

При обратном преобразовании звезды в эквивалентный треугольник, т.е. при заданных сопротивления r_A, r_Б, r_В:

	(2.6)
	(2.7)
	(2.8)

Таким образом, сопротивление стороны эквивалентного треугольника равно сумме сопротивлений двух лучей звезды, присоединенных к тем же вершинам, что и сторона треугольника, и их произведения, деленного на сопротивление третьего луча звезды.


2.4 ЭКВИВАЛЕНТНЫЕ СХЕМЫ ИСТОЧНИКОВ ЭНЕРГИИ
При расчетах электрических цепей реальные источники электрической энергии заменяются одной из двух эквивалентных схем.

Первая схема замещения, состоящая из идеального источника ЭДС Е и внутреннего сопротивления r_вт, была рассмотрена ранее.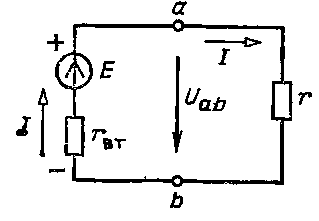


Рис. 2.7 Простейшая электрическая цепь постоянного тока
Вторая схема замещения источника, показана на рис. 2.8. Она состоит из идеального источника тока, изображенного кружком с двумя стрелками внутри и буквой Iк рядом, внутреннее сопротивление которого бесконечно велико, и параллельно присоединенного внутреннего сопротивления r_вт источника питания.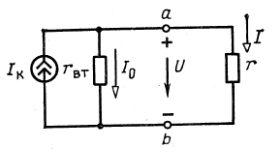



Рис. 2.8 Схема замещения реального источника тока
Источник, ток которого не зависит от нагрузки (тока I) и сопротивления r и равен Iк, и называют источником тока. Стрелки внутри кружка показывают направление тока источника. Таким образом, вторая возможная схема замещения (рис. 2.8) также состоит из двух элементов: идеального источника тока и сопротивления r_вт, равного внутреннему сопротивлению реального источника питания.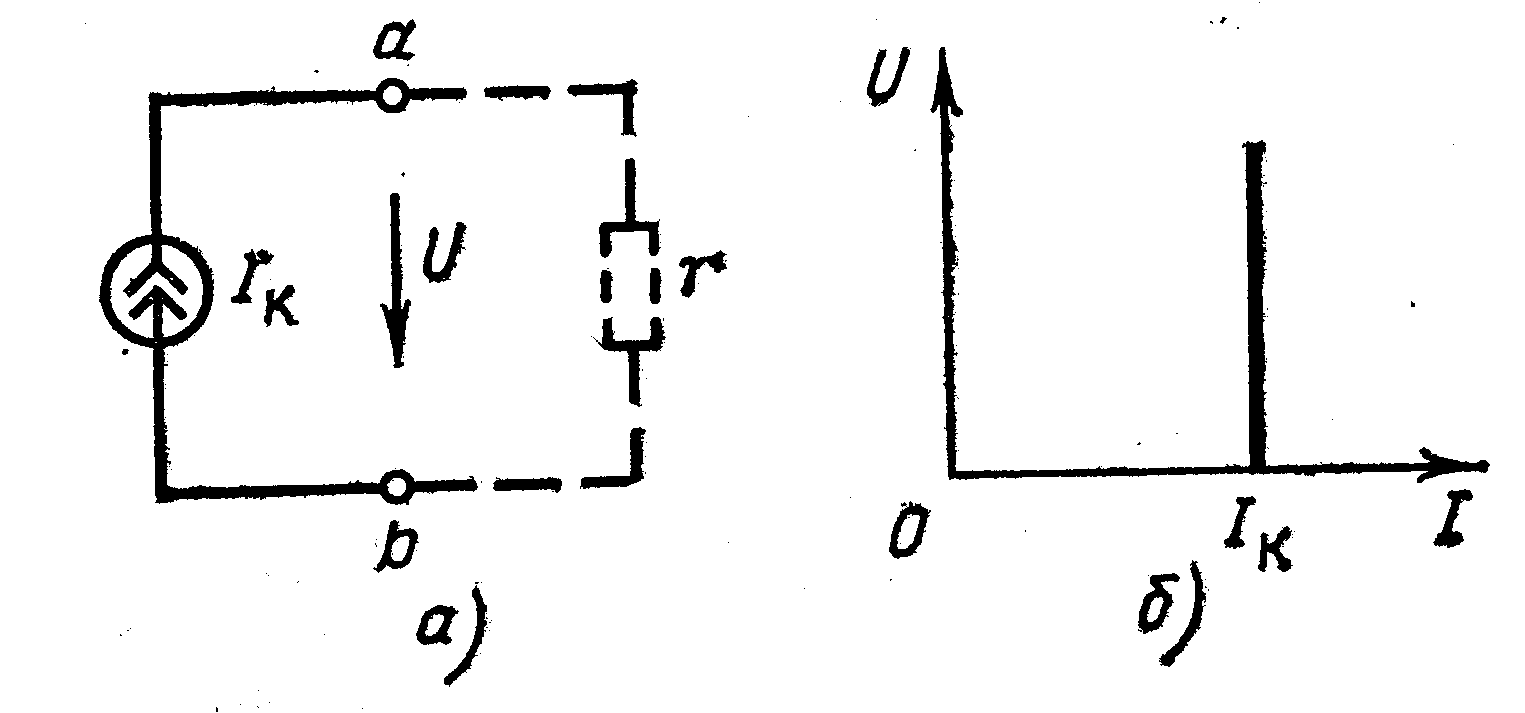



Рис. 2.9 Обозначение идеального источника тока (а) и его внешняя характеристика (б)
Идеальный источник тока показан на рис. 2.9,а, так как в схеме замещения отпадает ветвь с сопротивлением r_вт. Ток идеального источника тока не зависит от сопротивления нагрузки и остается равным I_к. Внешняя характеристика идеального источника тока показана на рис. 2.9,б. В этом случае при изменяющейся нагрузке напряжение приемника изменяется пропорционально сопротивлению приемника, так как по закону Ома U=rI_k, а ток равен постоянной величине I_к.