Лекция 2 ВИДЫ СОЕДИНЕНИЙ В ЭЛЕКТРИЧЕСКОЙ ЦЕПИ. ЛК_2_Виды_соединений_эл_элементов (2). Лекция 2 Виды соединений в электрической цепи
 Скачать 197.32 Kb. Скачать 197.32 Kb.
|
Лекция 2Виды соединений в электрической цепиТипы электрических соединений и их преобразованиеРазличают четыре вида соединений электрических элементов между собой: Последовательное Параллельное Соединение треугольником (многоугольником) Соединение 3-х лучевой звездой (многолучевой звездой) Не следует выделять смешанное соединение в какой-то самостоятельный тип соединения. Последовательное соединение резисторовВнешний признак последовательного соединения – элементы следуют друг за другом, то есть конец («к») одного соединён с началом («н»)следующего, конец следующего – с началом последующего и так далее. 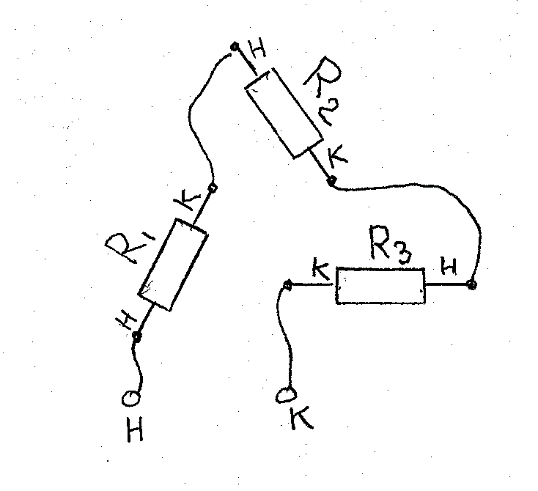 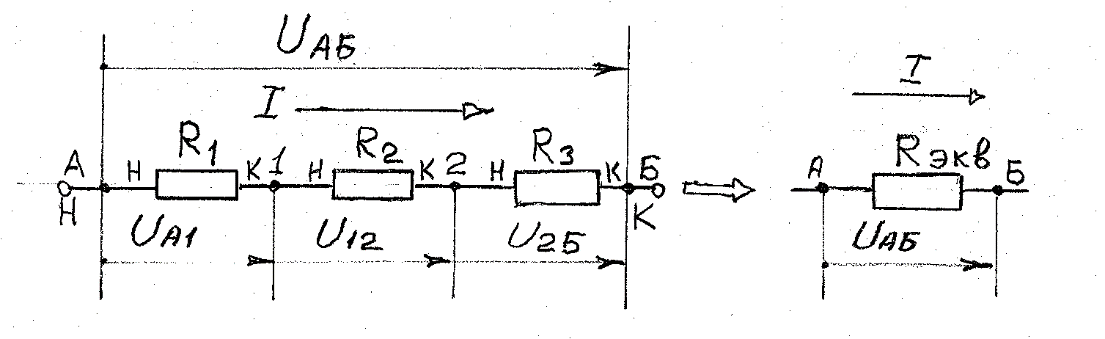 Рисунок 3. Последовательное соединение резисторов Следовательно, ветвь это всегда последовательное соединение элементов. Отсюда электрический признак последовательного соединения – через все элементы соединённые последовательно протекает один и тот же электрический ток (одной и той же силы). Если в какой-то ветви есть два последовательно соединенных резистора R1 и R2 , то через них протекает один и тот же ток, в обозначениях или I1 (или I2). Совершенно очевидно, что каждый из последовательно соединённых резисторов на своём участке окажет сопротивление току. Тогда общее сопротивление будет равно сумме всех сопротивлений и все последовательно соединённые резисторы можно заменить на этом участке одним эквивалентным резистором, сопротивление которого равно сумме сопротивлений всех резисторов. Rэкв = 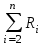 Этот вывод не противоречит закону Ома для участка цепи. На рисунке 3 участок А-Б содержит три последовательно соединённых резистора. Этот участок содержит три участка А-1, 1-2 и 2-Б. Из рисунка видно, что 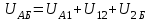 Заменим падения напряжения по закону Ома 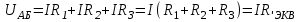 то есть эквивалентное сопротивление   = R1+R2+R3 = R1+R2+R3В электротехнике преобразование является эквивалентным, если потенциалы крайних точек преобразуемого участка (у нас А и Б) после преобразования не изменятся. Параллельное соединение резисторовВнешний признак параллельного соединения – «лестница» из резисторов. Все начала резисторов соединены вместе и все концы резисторов также соединены вместе, то есть начала и концы образуют узлы Н и К. Следовательно, все резисторы, соединённые параллельно, находятся под одним и тем же напряжением. 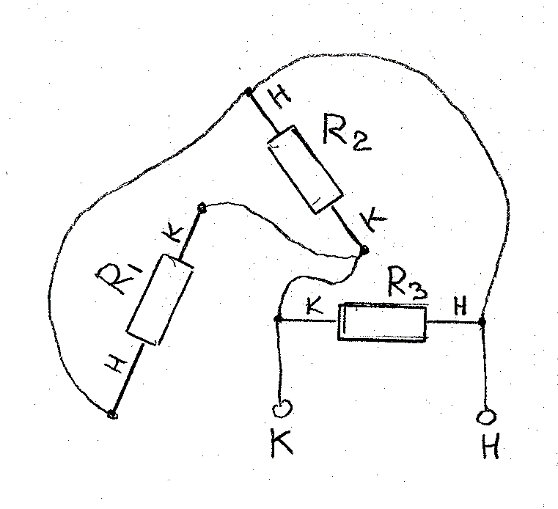 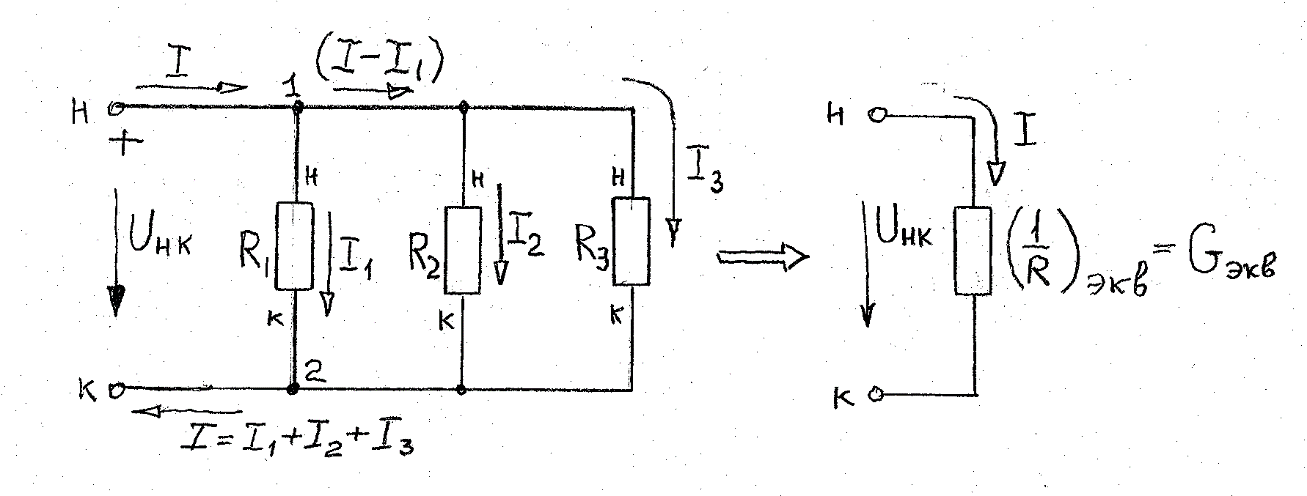 Рисунок 4. Параллельное соединение резисторов В каждом резисторе, соединённым параллельно с другими будет находиться свой ток, который по закону Ома для участка цепи 1-2 равен 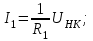 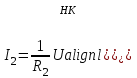 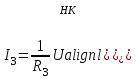 После узла «2» все токи соединятся в общий ток I. Следовательно, после простого преобразования, получим правую эквивалентную схему 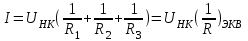 Величина 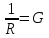 называется проводимостью, следовательно, формула преобразования для параллельно соединённых резисторов называется проводимостью, следовательно, формула преобразования для параллельно соединённых резисторов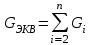 Очень часто приходится преобразовывать два параллельно соединённых резистора 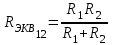 Интересный вывод: эквивалентное сопротивление параллельно соединённых резисторов всегда меньше меньшего сопротивления. Соединение треугольником и звездойСоединение треугольником и звездой представлены на рисунке 5. 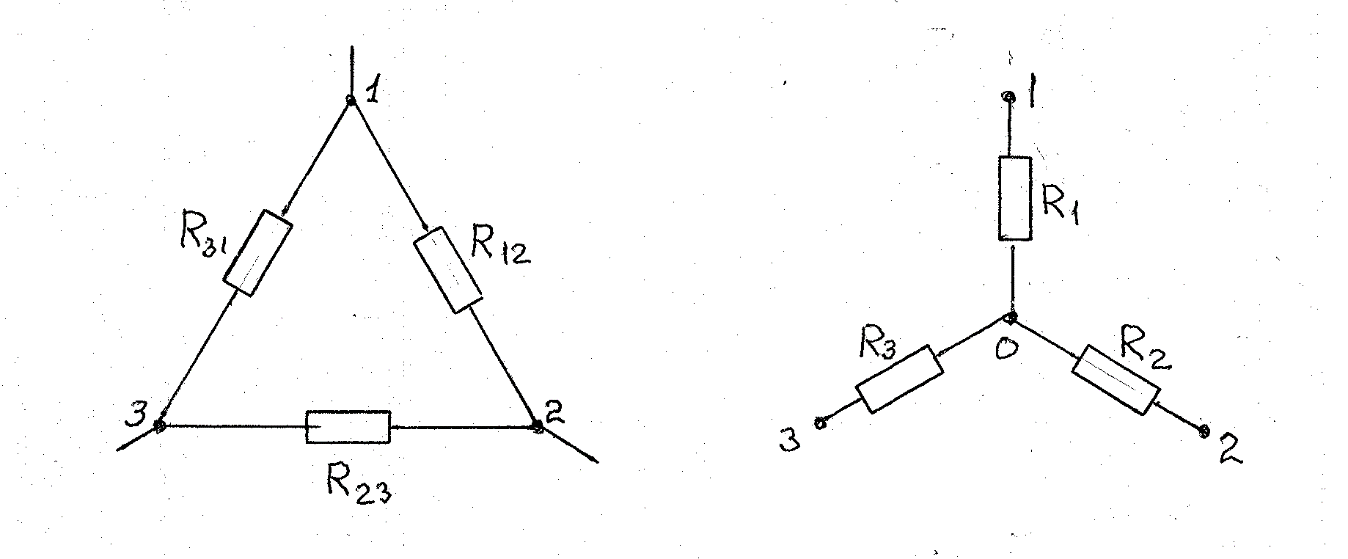 Рисунок 5. Соединение треугольником и звездой Цифрами в треугольнике помечены узлы, поэтому никакого последовательного соединения в треугольнике нет. Справа изображена эквивалентная этому треугольнику звезда. Точки на ветвях звезды т.1, т.2, т.3, это бывшие узлы треугольника, их потенциалы не изменились. Треугольник образует контур. Преобразуя треугольник в звезду, контур пропадает, следовательно, схема становится проще. Обычно в схемах треугольники изображены в виде четырёхугольников, поэтому как треугольники они в глаза не бросаются (рисунок 6). 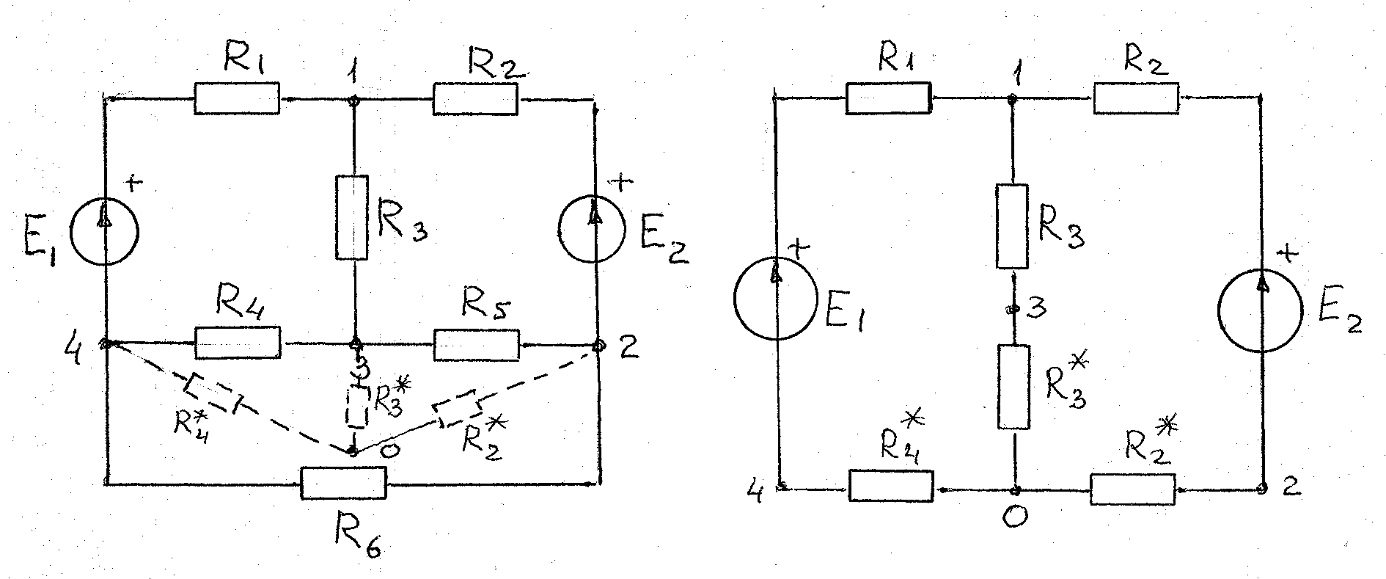 Исходная схема преобразованная схема Рисунок 6. Преобразование треугольника в звезду Исходная схема (левая) содержит три независимых контура (по ячейкам), а правая уже на один контур меньше. В исходной схеме узлы «2», «3», «4» являются вершинами треугольника со сторонами R4 R6 R5 . Чтобы не ошибиться в преобразовании необходимо внутри треугольника, изобразить звезду, которая должна получиться после преобразования, а резисторы звезды пометить звёздочкой. Формулы преобразования даются без доказательства. 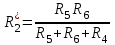 Формулу легко запомнить, она напоминает формулу эквивалентного сопротивления для двух параллельно соединённых резисторов, в числителе – произведение, в знаменателе – сумма, но сумма всех сторон треугольника. В числителе произведение резисторов, которые соединяются в рассматриваемом узле. Определяется сопротивление 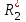 , то есть узел 2, там соединяются R5и R6 . Аналогично самостоятельно напишите формулы для определения , то есть узел 2, там соединяются R5и R6 . Аналогично самостоятельно напишите формулы для определения 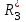 и и 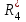 . .Такое преобразование целесообразно использовать в случаях, когда не требуется знать величину тока в сопротивлениях треугольника, так как они исчезают в преобразованной схеме, а чтобы найти токи в них, нужно вернуться к исходной схеме и несколько раз применить закон Ома для участка цепи. Например, нужна сила тока в R4, то есть нужно знать напряжение на участке 3-4. Это напряжение можно найти как разность потенциалов точек 3 и 4, используя преобразованную схему, в которой найдены все токи. Как это делается, рассматривалось в разделе «Закон Ома для активного участка цепи». Мы рассмотрели все виды соединений и их преобразование. |
