Магнитное поле. Магнитное_поле. Лекция 3 Магнитное поле 39. Магнитное поле

• Название: Лекция 3 Магнитное поле 39. Магнитное поле
• Анкор: Магнитное поле
• Дата: 13.05.2022
• Размер: 0.64 Mb.
• Имя файла: Магнитное_поле.doc
• Тип: Лекция; #528143
• страница: 2 из 3

52. Магнитное поле тороида.

П 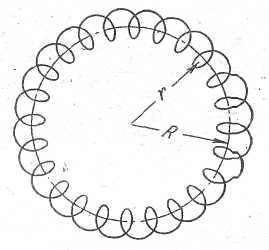усть контур – окружность радиуса r. Вектор - касательная к контуру в каждой точке, следовательно,

Если контур внутри обмотки тороида, то он охватывает ток , тогда , . Для контуров вне обмотки сумма охватываемых токов равна 0, следовательно, В=0.

53. Поток вектора магнитной индукции.

Магнитный поток через площадку dS: , где - проекция вектора на направление нормали к площадке dS,  - угол между векторами и .

Знак потока связывают направлением тока в контуре. Если собственный вектор контура совпадает с внешним, то Ф>0.

Поток вектора через произвольную поверхность S: .

Если поле однородно, тогда [Вб] – вебер.

54. Теорема Гаусса для магнитного поля в вакууме.

Поток вектора магнитной индукции сквозь замкнутую поверхность равен нулю: (т.е. отражает факт отсутствия магнитных зарядов, в отличие от электрических).

55. Работа по перемещению проводника с током в магнитном поле.

Рассмотрим перемещение проводника длиной l с током I в магнитном поле с индукцией В.

Проводник перемещается под действием силы Ампера: .

Работа при перемещении:

( , ).
Магнитное поле в веществе

56. Магнитные моменты электрона.

Всякое вещество под действием магнитного поля способно приобретать магнитный момент (намагничиваться), т.е. является магнетиком.

В молекулах вещества электроны, вращающиеся вокруг ядер, можно рассматривать как круговые микротоки создающие собственные магнитные поля. В отсутствие внешнего поля молекулярные токи ориентированы хаотически и результирующее поле в веществе равно 0. Под воздействием внешнего поля магнитные моменты молекул ориентируются в одном направлении и вещество намагничивается – суммарный магнитный момент не равен 0.

Магнитный момент электрона: , где r – радиус орбиты электрона, – число оборотов в секунду. Направление образует правовинтовую систему с направлением тока.

- скорость электрона, тогда - орбитальный магнитный момент электрона.

Электрон обладает массой, следовательно, моментом: - орбитальный механический момент. Направление L образует правовинтовую систему с направлением движения электрона.










-e





I


Отношение магнитного момента элементарной частицы к её механическому моменту называется гиромагнитным отношением. Для электрона:

57. Диа- и парамагнетики.

На вращающийся по орбите электрон, как на замкнутый ток, во внешнем магнитном поле действует вращающий момент сил. В результате электрон приобретает дополнительное равномерное вращение, при котором вектор описывает конус вокруг направления вектора с некоторой угловой скоростью . Такое движение называется прецессией.

Торема Лармора: действие магнитного поля на электронную орбиту можно свести к сообщению этой орбите прецессии с угловой скоростью .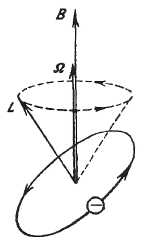



Прецессионное движение обит эквивалентно дополнительному круговому микротокутоку, магнитный момент которого направлен против внешнего поля. Наведённые составляющие магнитных полей всех атомов складываются и образуют собственное магнитное поле вещества, ослабляющее внешнее магнитное поле. Данный эффект – диамагнитный, а вещества, создающие во внешнем магнитном поле противоположно направленное поле – диамагнетики (Ag, Au, Cu…). Диамагнетизм свойственен всем веществам.

Парамагнетики – вещества, магнитные моменты молекул которых даже в отсутствие внешнего магнитного поля не равны 0 (Pt, Al…). Магнитные моменты молекул парамагнетиков ориентированы хаотично, поэтому в отсутствие внешнего поля магнитные свойства не наблюдаются. При внесении парамагнетика во внешнее поле устанавливается преимущественная ориентация магнитных моментов молекул по полю. Если парамагнитный момент молекул превосходит диамагнитный, тогда суммарный магнитный момент молекул сонаправлен с внешним полем и оно усиливается.

Пусть внешнее поле неоднородно. Рассмотрим виток с током (каждую молекулу во внешнем поле можно представить как виток с током результирующий магнитный момент которого, в зависимости от типа вещества, направлен либо по полю либо против него).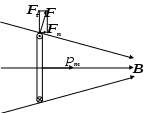



Нормальная составляющая силы, действующей на виток направлена перпендикулярно плоскости витка и вызывает его перемещение. Для диамагнетиков вектора и противоположны и сила будет выталкивать виток из области большего поля. У парамагнетиков и сонаправлены и сила будет втягивать виток в область большего поля.

58. Вектор напряжённости магнитного поля.

Р 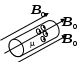ассмотрим круглый стержень во внешнем магнитном поле . Под действием этого поля все молекулярные токи стержня ориентируются в плоскости, перпендикулярной вектору .

Результирующее поле внутри стержня оказывается равным: , где  - относительная магнитная проницаемость среды. Для описания внешнего поля вводится вектор напряжённости магнитного поля , не зависящий от свойств среды.

, где – магнитная постоянная

Таким образом, вектор - аналог вектора напряжённости электростатического поля , а вектор - аналог вектора электрического смещения .

59. Намагниченность

Намагниченность – магнитный момент единицы объёма магнетика. , где - векторная сумма магнитных моментов всех молекул.

Аналогично диэлектрической восприимчивости вводится понятие магнитной восприимчивости: .

Для диамагнетиков <0, для парамагнетиков >0, .

Поле в веществе складывается из поля внешнего и поля намагниченного вещества  . .

Для описания поля, создаваемого молекулярными токами, рассмотрим магнетик в виде цилиндра длиной l и сечением S. Поле параллельно оси цилиндра. Внутри цилиндра молекулярные токи компенсируют друг друга. На поверхности цилиндра токи нескомпенсированы и появляется ток . Пусть =1. Цилиндр можно представить соленоидом длиной l, с одним витком (N=1).





Магнитный момент тока : , где V – объём магнетика.

Намагниченность , следовательно, ( ).

Окончательно, .

Величина - относительная магнитная проницаемость вещества.

Для диамагнетиков , для парамагнетиков .

60. Теорема о циркуляции магнитного поля в веществе.

Циркуляция вектора магнитной индукции по произвольному замкнутому контуру равна алгебраической сумме токов проводимости и молекулярных токов, охватываемых этим контуром, умноженной на магнитную постоянную:

, где I и I’ – алгебраические суммы токов проводимости (макротоков) и молекулярных токов (микротоков).

Циркуляция намагниченности по произвольному замкнутому контуру L равна алгебраической сумме молекулярных токов, а циркуляция вектора - сумме токов проводимости, охватываемых контуром:



- теорема о циркуляции вектора .

Учитывая, , где S – поверхность охватываемая контуром L, тогда .

60. Условия на границе раздела двух магнетиков.

Пусть на границе магнетиков отсутствуют токи проводимости.

Рассмотрим цилиндр бесконечно малой высоты, основания которого, расположены в разных средах.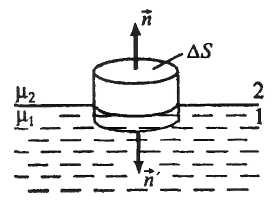



По теореме Гаусса: (“-”, т.к. ), следовательно .

, тогда

Выделим на границе сред контур ABCD.



Токов проводимости нет, следовательно, согласно теореме о циркуляции: . (Интегралы по AD и BC равны 0, т.к. AD и BC можно взять бесконечно малые). , , .

Таким образом, при переходе через границу раздела двух магнетиков нормальная составляющая вектора и тангенциальная составляющая вектора меняются непрерывно, а тангенциальная составляющая вектора и нормальная составляющая вектора претерпевают скачок.

61. Ферромагнетики.

Ф ерромагнетики – вещества, сохраняют намагниченность при отсутствии внешнего поля. Характерная особенность - ( ).

Зависимость индукции поля от напряжённости в ферромагнетике:




Зависимость :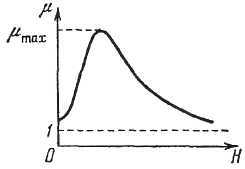


Зависимость намагниченности J от напряжённости Н поля в ферромагнетике определяется предыдущим намагничиванием. Это явление – магнитный гистерезис.



Участок 0-1 - основная кривая намагничивания. При уменьшении Н кривая намагничивания идёт по другому пути 1-2 и при Н=0 есть остаточная намагниченность J_ос. Это явление используется при изготовлении постоянных магнитов.

Чтобы уменьшить намагниченность до 0 необходимо приложить противоположно-направленное поле с напряжённостью Н_с (2-3). При дальнейшем увеличении противоположного поля ферромагнетик вновь перенамагничивается до –J_нас (3-4). Перенамагничивание до J_нас происходит по другому пути 4-5-6-1.

В итоге получается петля гистерезиса.

Ферромагнетик состоит из микроскопических областей – доменов, самопроизвольно намагничивающихся до насыщения. Направления намагничивания доменов произвольное. При отсутствии поля магнитные моменты доменов компенсируют друг друга и в целом ферромагнетик не намагничен. Внешнее поле ориентирует домены по полю. Насыщение - если все домены ориентированы по полю.

Площадь петли гистерезиса пропорциональна энергии, затраченной в процессе перемагничивания. Эта энергия превращается во внутреннюю энергию ферромагнетика, т.е. он нагревается. Ферриты – с очень маленькой площадью петли.

Температура при которой ферромагнетик теряет магнитные свойства – точка Кюри (превращается в парамагнетик). Для железа 768С, для никеля 365С.

Электромагнитная индукция