Лекция 4. Лекция 4 Логика предикатов Понятие предиката

• Название: Лекция 4 Логика предикатов Понятие предиката
• Анкор: Лекция 4
• Дата: 02.11.2022
• Размер: 39.81 Kb.
• Имя файла: Lekcija_4.docx
• Тип: Лекция; #766931

Лекция 4
Логика предикатов

Понятие предиката

В алгебре логики высказывания рассматриваются как нераздельные целые и только с точки зрения их истинности или ложности. Ни структура высказываний, ни, тем более, их содержание не затрагиваются. В то же время и в науке, и в практике используются заключения, существенным образом зависящие как от структуры, так и от содержания используемых в них высказываний.

Например, в рассуждении «Всякий ромб – параллелограмм; ABCD– ромб; следовательно, ABCD– параллелограмм» посылки и заключение являются элементарными высказываниями логики высказываний и с точки зрения этой логики рассматриваются как целые, неделимые, без учета их внутренней структуры. Следовательно, алгебра логики, будучи важной частью логики, оказывается недостаточной в анализе многих рассуждений.

В связи с этим возникает необходимость в расширении логики высказываний, в построении такой логической системы, средствами которой можно было бы исследовать и структуру тех высказываний, которые в рамках логика высказываний рассматриваются как элементарные.

Такой логической системой является логика предикатов, содержащая всю логику высказываний в качестве своей части.

Логика предикатов, как и традиционная формальная логика, расчленяет элементарное высказывание на субъект (буквально – подлежащее, хотя оно и может играть роль дополнения) и предикат (буквально – сказуемое, хотя оно может играть и роль определения).

Субъект – это то, о чем что-то утверждается в высказывании; предикат – это то, что утверждается о субъекте.

Например, в высказывании «7 – простое число», «7» – субъект, «простое число» – предикат. Это высказывание утверждает, что «7» обладает свойством «быть простым числом».

Определение 4.1. Одноместным предикатом Р(х) называется произвольная функция переменного х, определенная на множестве М и принимающая значения из множества {1, 0}.

Определение 4.2. Множество М, на котором определен предикат Р(х), называется областью определения предиката.

Определение 4.3. Множество всех элементов хМ, при которых предикат принимает значение «истина», называется множеством истинности предиката Р(х), то есть множество истинности предиката Р(х) – это множество

I_р={х: хМ, Р(х)=l}.

Например, предикат Р(х) – «x – простое число» определен на множестве N, а множество I_рдля него есть множество всех простых чисел. Предикат
Q(x) – «sin(х)=0» определен на множестве R, а его множество истинности I_q={kπ, kZ}. Предикат F(x) – «Диагонали параллелограмма х перпендикулярны» определен на множестве всех параллелограммов, а его множеством истинности является множество всех ромбов.

Определение 4.4. Предикат Р(х), определенный на множестве М, называется тождественно истинным (тождественно ложным), если I_р= М (I_р= ).

Естественным обобщением понятия одноместного предиката является понятие многоместного предиката, с помощью которого выражаются отношения между предметами.

Определение 4.5. Двухместным предикатом Р(х,у) называется функция двух переменных х и у, определенная на множестве М = М₁× М₂ и принимающая значения из множества {1,0}.

Аналогично определяется n-местный предикат.

Логические операции над предикатами

Пусть на некотором множестве М определены два предиката Р(х) и Q(х).

Определение 4.6. Конъюнкцией двух предикатов Р(х) и Q(х) называется новый предикат Р(х) ÙQ(x), который принимает значение «истина» при тех и только тех значениях х  М, при которых каждый из предикатов принимает значение «истина», и принимает значение «ложь» во всех остальных случаях.

Очевидно, что областью истинности предиката P(x) ÙQ(x) является общая часть областей истинности предикатов P(x)и Q(x), то есть пересечение I_р ∩ I_q.

Операции дизъюнкции, отрицания и импликации вводятся аналогично.

Кванторные операции

Пусть имеется предикат Р(х), определенный на множестве М. Если а – некоторый элемент из множества М,то подстановка его вместо х в предикат Р(х) прекращает этот предикат в высказывание Р(а). Такое высказывание называется единичным. Наряду с образованием из предикатов единичных высказываний в логике предикатов рассматривается еще две операция, которые превращают одноместный предикат в высказывание.

1. Квантор всеобщности. Пусть Р(х) – предикат, определенный на множестве М. Под выражением xР(х) понимают высказывание, истинное, когда Р(х) истинно для каждого элемента х из множества М и ложное в противном случае. Это высказывание уже не зависит от х. Соответствующее ему словесное выражение будет «Для всякого х Р(х) истинно». Символ  называют квантором всеобщности.

Переменную х в предикате Р(х) называют свободной (ей можно придавать различные значения из М), в высказывании х Р(х) переменную х называют связанной квантором .

2. Квантор существования. Пусть Р(х) – предикат, определенный на множестве М. Под выражением $хР(х) понимают высказывание, которое является истинным, если существует элемент хМ, для которого Р(х) истинно, и ложным в противном случае. Это высказывание уже не зависит от х. Соответствующее ему словесное выражение будет: «Существует х,при котором Р(х) истинно». Символ $ называют квантором существования. В высказывании $хР(х) переменная х связана квантором $.

Ясно, что высказывание хР(х) истинно только в том единственном случае, когда Р(х) – тождественно истинный предикат, а высказывание $хР(х) ложно только в том единственном случае, когда Р(х) – тождественно ложный предикат.

Формулы логики предикатов

Расширение логики высказываний до логики предикатов получается за счет включения в формулы утверждений, являющихся предикатами. Но при этом, поскольку предикаты относятся к изучаемым объектам, необходимо включить в теорию и сами объекты а₁,…, а_n,…Поэтому, чтобы дать определение формул в логике предикатов, нужно уточнить принципы описания в логике предикатов объектов. Делается это с помощью понятия терм.

Определение 4.7. Дадим следующее определение терма:

1) переменные х₁,…, х_п ,… для объектов – это термы;

2) если f(∙,…,∙) функция п-переменных, ставящая в соответствие изучаемым объектам объект, и t₁,…,t_n термы, то f(t₁,…,t_n) – терм.

Определение 4.8. Определение формулы логики предикатов:

1) если Р(∙,…,∙) п-местный предикат, a t₁,…,t_n – термы, то Р(t₁,…,t_n) – формула;

2) если А и В формулы, то (А Ù B), (AB), (AB) – формулы;

3) если A формула, то ¬A – формула;

4) если А(х) – формула, содержащая переменную х, то хА(х), хА(х) – формулы.

О логическом значении формулы логики предикатов можно говорить лишь тогда, когда задано множество М,на котором определены входящие в эту формулу предикаты. Логическое значение формулы логики предикатов зависит от значений термов.

При конкретных значениях каждого из термов формула логики предикатов становится высказыванием, имеющим истинное или ложное значение.

Равносильные формулы логики предикатов

Определение 4.9. Две формулы логики предикатов А и В называются равносильными на области М, если они принимают одинаковые логические значения при всех значениях входящих в них переменных, отнесенных к области М.

Определение 4.10. Две формулы логики предикатов А и В называются равносильными, если они равносильны на всякой области.

Здесь, как в алгебре высказываний, для равносильных формул принято обозначение А  В.

Ясно, что все равносильности алгебры высказываний будут верны, если в них вместо переменных высказываний подставить формулы логики предикатов. Но, кроме того, имеют место равносильности самой логики предикатов. Рассмотрим основные из этих равносильностей. Пусть А(х) и В(х) – переменные предикаты, а С – переменное высказывание. Тогда

1. 
   ,
   
2. 
   ,
   
3. 
   ,
   
4. 
   ,
   
5. 
   ,
   
6. 
   ,
   

7. 
   ,
   
8. 
   ,
   
9. 
   ,
   

10. 
    ,
    
11. 
    ,
    

12. 
    ,
    
13. 
    ,
    
14. 
    ,
    
15. 
    .
    

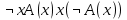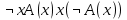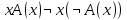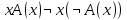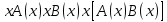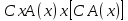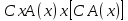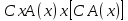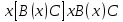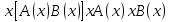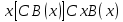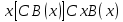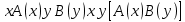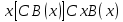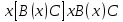Предваренная нормальная форма

Определение 4.11. Говорят, что формула логики предикатов имеет нормальную форму, если она содержит только операции отрицания, конъюнкции, дизъюнкции и кванторные операции.

Используя равносильности алгебры высказываний и логики предикатов, каждую формулу логики предикатов можно привести к нормальной форме.

Среди нормальных форм формул логики предикатов важное значение имеют так называемые предваренные нормальные формы (п.н.ф.). В них кванторные операции либо полностью отсутствуют, либо они используются после всех операций алгебры логики, то есть предваренная нормальная форма формулы логики предикатов имеет вид:

(σх₁)(σх₂)...(σх_п) А(х₁, х₂,..., х_т), п≤т,

где под символом (σx_i) понимается один из кванторов х_i или $х_i, а формула А кванторов не содержит.

Теорема 4.1. Всякая формула логики предикатов может быть приведена к предваренной нормальной форме.

Алгоритм получения предваренной формы для произвольной формулы логики предикатов включает следующие шаги.

1. Исключение связок импликации и эквивалентности.

2. Переименование (если необходимо) связанных переменных таким образом, чтобы никакая переменная не имела бы одновременно свободных и связанных вхождений. Это должно быть выполнено для всех подформул рассматриваемой формулы.

3. Удаление кванторов, область действия которых не содержит вхождений квантифицированной переменной.

4. Сужение области действия отрицаний и снятие двойных отрицаний.

5. Перенос всех кванторов в начало формулы (для этого используются основные равносильности).

Сколемовская форма и сколемизация формул

В формуле, представленной в предваренной нормальной форме, легко добиться, чтобы последними стояли кванторы существования. Для этого используется тождество:

В(х₁,…,z₁,…) ≡ $u[B(х₁,…, z₁,…) ÙI(u)],

где I(и) –произвольная общезначимая формула.

Например, формула имеет вид

$х₁…$х_kу₁…у_m$z₁…$z_р В(х₁,…, х_k, у₁,…, у_m, z₁,…, z_р,…)(*)

Будем теперь «снимать» в формуле (*)последовательно группы кванторов слева направо, заменяя их на функции. Основная идея здесь состоит в том, что пара кванторов u$v – это функция v=f(u). Следовательно, набору кванторов у₁…у_m$z_i отвечает функция z_i= g_i(у₁,…, у_m).Если самой левой группой кванторов являются кванторы существования $х₁…$х_k, то им соответствуют постоянные функции, которые сводятся к заданию их значенийa₁,…, a_k.

Сняв группу кванторов в формуле (*), в функции В оставляем переменные у₁,…, у_m, по которым стояли кванторы всеобщности, а вместо следующих за ними переменных z₁,…, z_р, связанных кванторами существования, подставляем полученные функции g_i(y₁,…, y_m).

В результате имеем набор функций

a₁,…, a_k, g₁(y₁,…, y_m),…,g_p(y₁,…, y_m),… (**)

и формулу

B(a₁,…, a_k, y₁,…, y_m,g₁(y₁,…,y_m),…,g_p(y₁,…,y_m),…) (***)

Определение 4.12. Формула логики предикатов называется замкнутой, если она не содержит свободных предметных переменных.

Определение 4.13. Сколемовская форма – это замкнутая предваренная форма, префикс которой содержит только кванторы всеобщности – .

Приведение формулы логики предикатов к сколемовской форме называется сколемизацией.

Общезначимость и выполнимость формул

Определение 4.14. Формула А логики предикатов называется выполнимой в области М, если существуют значения переменных, входящих в эту формулу и отнесенных к области М, при которых формула А принимает истинные значения.

Определение 4.15. Формула А называется выполнимой, если существует область, на которой эта формула выполнима.

Из определения 4.15 следует, что, если формула выполнима, то это еще не означает, что она выполнима в любой области.

Определение 4.16. Формула А называется тождественно истинной в области М, если она принимает истинные значения для всех значений переменных, входящих в эту формулу и отнесенных к этой области.

Определение 4.17. Формула А называется общезначимой, если она тождественно истинная на всякой области.

Определение 4.18. Формула А называется тождественно ложной в области М, если она принимает ложные значения для всех значений переменных, входящих в эту формулу и отнесенных к этой области.

Из приведенных определений следует:

1) если формула А общезначима, то она и выполнима на всякой области;

2) если формула А тождественно истинная в области М, то она и выполнима в этой области;

3) если формула А тождественно ложная в области М, то она не выполнима в этой области;

4) если формула А не выполнима, то она тождественно ложна на всякой области.

В связи с данными определениями естественно выделить два класса формул логики предикатов: выполнимых и не выполнимых формул.

Отметим, что общезначимую формулу называют логическим законом.

Теорема 4.2. Для того, чтобы формула А была общезначима, необходимо и достаточно, чтобы ее отрицание было не выполнимо.

Теорема 4.3. Для того, чтобы формула А была выполнимой, необходимо и достаточно, чтобы формула А была не общезначима.

Проблема разрешимости для общезначимости и выполнимости,
неразрешимость ее в общем случае

Проблема разрешимости в логике предикатов ставится так же, как и в алгебре логики: существуют ли алгоритмы, позволяющие для любой формулы А логики предикатов установить, к какому классу она относится, то есть является ли она или общезначимой, или выполнимой, или тождественно ложной. Если бы такой алгоритм существовал, то, как и в алгебре высказываний, он сводился бы к критерию тождественной истинности любой формулы логики предикатов.

Отметим, что в отличие от алгебры логики, в логике предикатов не применим метод перебора всех вариантов значений переменных, входящих в формулу, так как таких вариантов может быть бесконечное множество.

В 1936 году американский математик А.Черч доказал, что проблема разрешимости логики предикатов в общем виде алгоритмически не разрешима, то есть не существует алгоритма, который бы позволил установить, к какому классу формул относится любая формула логики предикатов.

Алгоритмы распознавания общезначимости формул
в частных случаях

1. Проблема разрешимости в случае конечных областей.

Очевидно, что проблема разрешимости в случае конечных областей разрешима. Действительно, в этом случае кванторные операции можно заменить операциями конъюнкции и дизъюнкции и тем самым свести формулу логики предикатов к формуле алгебры логики, для которой проблема разрешимости разрешима.

2. Проблема разрешимости для формул, содержащих в предваренной нормальной форме кванторы одного типа.

Определение 4.19. Если формула логики предикатов С содержит свободные переменные х₁, х₂,..., х_п, то формула

А = х₁х₂ ... х_п С(х₁, х₂,..., х_п)

называется замыканием общности формулы С, а формула

В = $х₁$х₂ ... $х_п С(х₁, х₂, ..., х_п)

называется замыканием существования формулы С.

Теорема 4.4. Если замкнутая формула логики предикатов в предваренной нормальной форме содержит только кванторы существования, число которых равно п, и тождественно истинна на любой области, состоящей из одного элемента, то она общезначима.

Теорема 4.5. Если замкнутая формула логики предикатов в предваренной нормальной форме содержит только кванторы общности, число которых равно га, и тождественно истинна на всяком множестве, содержащем не более, чем п элементов, то она общезначима.