механика грунтов, конспект лекций. Лекция 4 Основные понятия курса. Цели и задачи курса. Состав, строение, состояние и физические свойства грунтов. 4

• Название: Лекция 4 Основные понятия курса. Цели и задачи курса. Состав, строение, состояние и физические свойства грунтов. 4
• Анкор: механика грунтов, конспект лекций.doc
• Дата: 09.04.2017
• Размер: 2.19 Mb.
• Имя файла: механика грунтов, конспект лекций.doc
• Тип: Лекция; #4663
• страница: 8 из 15

3.3.2. Плоская задача. Действие равномерно распределенной нагрузки.

Схема для расчета напряжений в основании в случае плоской задачи при действии равномерно распределенной нагрузки интенсивностью показана на рис. 3.6.а.

Точные выражения для определения компонент напряжений в любой точке упругого полупространства были получены Г. В. Колосовым в виде:

; ; , (3.9)

где , , - коэффициенты влияния, зависящие от безразмерных параметров и ; и – координатные точки, в которой определяются напряжения; – ширина полосы загружения.

На рис. 3.7. а-в показано в виде изолиний распределение нарпряжении 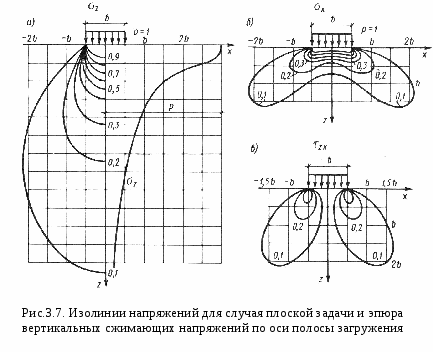, и в массиве грунте для случая плоской задачи.




В некоторых случаях при анализе напряженного состояния основания оказывается удобнее пользоваться главными напряжениями. Тогда значения главных напряжений в любой точке упругого полупространства под действием полосовой равномерно распределенной нагрузки можно определить по формулам И. Х. Митчелла:

, (3.10)

где - угол видимости, образованный лучами, выходящими из данной точки к краям загруженной полосы (рис.3.6.б).

3.3.3. Пространственная задача. Действие равномерно распределенной нагрузки.

В 1935 г. А. Лявом были получены значения вертикальных сжимающих напряжений в любой точке основания от действия нагрузки интенсивностью , равномерно распределенной по площади прямоугольника размером .

Практический интерес представляют компоненты напряжений 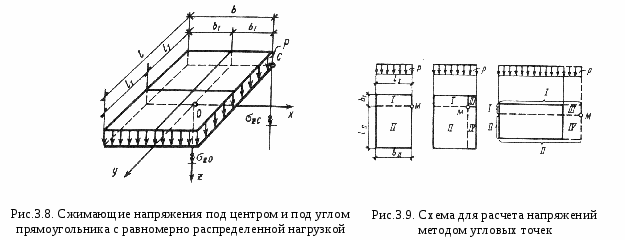, относящиеся к вертикали, проведенной через угловую точку этого прямоугольника, и , действующие по вертикали, проходящей через его центр (рис. 3.8.).



Используя коэффициенты влияния можно записать:

; , (3.11)

где - и - соответственно коэффициенты влияния для угловых и центральных напряжений, зависящие от соотношения сторон загруженного прямоугольника и относительной глубины точки, в которой определяются напряжения.

Между значениями и имеется определенное соотношение.

. (3.12)

Тогда оказывается удобным выразить формулы (3.11) через общий коэффициент влияния и записать их в виде:

; . (3.13)

Коэффициент зависит от безразмерных параметров и : , (при определении углового напряжения ), (при определении напряжения под центром прямоугольника ).